受多变量影响的闭环供应链模型研究

王绍凡 陈荔

摘 要：构建了由一个直接从事再制造活动的制造商和一个零售商组成的闭环供应链系统。假设产品的需求与产品的销售价格、产品的质量水平、制造商的回收努力和零售商的销售努力成线性关系，运用博弈论分析了闭环供应链系统在集中决策和3种分散决策下的最优策略。研究发现：闭环供应链系统在VN权力结构下的利润是3种分散决策模型中最大的，在MS权力结构下的利润是最小的。运用两部定价契约实现了不同权力结构下闭环供应链的协调。最后通过数值仿真验证了模型的合理性和不同权力结构下协调合同的有效性，并对主要的参数进行了敏感性分析。

关键词：闭环供应链；质量管理；回收努力；销售努力；博弈论

中图分类号：TP 391 文献标识码：A 文章编号：1672-7312（2016）04-0417-07

0 引 言

随着移动互联网的飞速发展和移动智能设备软硬件功能的不断完善，消费者对产品的需求日趋多样化和个性化。消费者不仅仅停留在对产品的质量和价格选择，越来越多的顾客对产品的服务更加重视。近些年，废旧品越来越多，资源浪费和环境污染问题日趋严重[1]。从产品的回收服务的角度而言，一个产品应具有可回收性。只有合理降低其产品回收成本，才能实现经济环保的和谐社会。如何有效协调产品的质量、服务水平和销售价格以及闭环供应链系统在不同权力结构下的协调成为国家和研究学者重点关注话题。

质量作为产品的一个重要属性，对供应链系统至关重要。熊中楷等[2]运用动态博弈论分析了制造商如何实现对零售商回收的再制造产品的数量和质量实施检验和控制。王文宾等[3]比较了闭环供应链系统在以回收率和回收量为基础的奖惩机制策略。Teunter等[4]研究了不同质量水平的回收产品问题，并得出了最佳的回收价格和再制造策略。谢家平等[5]将产品的质量水平作为内生变量，研究了再制造产品的质量差异与再制造比例的关系。肖迪等[6]研究了零售商采用收益共享契约对供应链成员质量控制决策的协调问题。景熠等[7]基于销售者对产品异质性需求，分析发现制造商生产再制造产品对新产品产生影响。聂佳佳等[8]研究了再制造产品质量对闭环供应链回收渠道选择的影响。Maiti等[9]分析了新产品和再制造产品的质量、产品的定价策略和旧产品的回收率以及闭环供应链系统的利润的变化。以上文献主要集中对产品的质量研究和服务水平作为消费者决定是否购买的一个关键决策。

大量文献研究了不同权力结构对供应链系统的影响和渠道冲突的协调机制。王文宾等[10]探讨了一个制造商和一个零售商组成的闭环供应链在不同权力结构下的定价策略和协调方法。聂佳佳等[11]研究了不同的战略联盟渠道结构对第三方负责回收闭环供应链的影响。Fan等[12]运用进化博弈理论分析了基于存货型的产品动态定价策略和生产规划问题。Hong等[13]研究发现制造商回收或者零售商回收对制造商而言是最有利的。Chuang等[14]研究发现制造商直接回收渠道所花费的回收费用最低。高举红等[15]探讨了销售商的低价促销决策或绿色促销决策对闭环供应链系统绩效的影响。Gao等[16]研究了回收服务、产品销售价格策略和销售努力水平对不同权力结构下闭环供应链的影响。Gurnani等[17]利用二部收费契约实现了不同合同结构的协调。张汉江等[18]运用最优激励理论，探讨了单一制造商采用激励契约合同可以实现闭环供应链系统成员间的协调。

综合以上文献，研究将制造商的产品质量、对再制造产品的回收努力水平和零售商的销售努力水平作为内生变量，并考虑不同权力结构，提出整个闭环供应链系统的最优策略。并通过零售商以最低销售价格为基准的契约合同，实现了不同权力结构下，整个闭环供应链系统的协调。最后，分析了产品质量、再制造品的回收努力和零售商销售努力，提高产品质量付出的固定成本和付出努力的固定成本对不同决策模型的最优解的影响。

1 问题及假设

构建了由一个制造商和一个零售商组成的闭环供应链系统。其中制造商制造新产品和回收旧产品用于再制造并将产品批发给零售商销售。假设新产品和再制造产品的功能和质量无差异，且消费者对产品的购买无选择性差异。首先，制造商将产品质量为q的商品以单位批发价格ω批发给零售商，假设制造商有足够的制造能力满足市场需求。零售商为获取单位产品纯利润t以单位销售价格p出售产品，并付出相应的销售努力g.制造商通过付出回收努力s并以单位价格A回收旧产品用于再制造。那么制造商和零售商如何确定最优的质量和服务以实现利润最大化呢？

为了便于模型的分析求解，做了如下主要假设：

1）大量文献[4，11，16]假设产品的质量成本是产品质量水平的二次函数。因此，假设产品的质量成本函数为（c1q2）/2，参数c1表示产品质量所付出的成本系数。

2）制造商对产品回收的投资收集努力为s.如广告的回收政策，逆向物流服务，货币激励和员工培训计划，从而增强产品的市场需求和回收率。假设产品的回收率η与制造商的回收努力水平s成正比。即：η=δs，δ为产品回收的比例系数。假设产品的回收努力成本函数为（c2s2）/2，参数c2表示产品回收努力所付出的成本系数。

3）零售商可以通过产品营销活动，广告宣传等销售努力扩大产品的销售量。假设零售商通过销售努力g而付出的销售努力成本函数为（c3g2）/2，参数c3表示零售商销售努力所付出的成本系数。为便于计算，我们假设c3=c2，表示零售商的销售努力与制造商的回收努力所付出的成本系数相同。

4）再制造产品与新产品无性能和质量差异，且在同一市场以相同的价格出售。新产品的制造成本为cm和再制造产品的制造成本为cr，则再制造产品的单位节约成本为c=cm-cr-A>0。

5）假设产品的需求量D是产品的销售价格p、产品的质量q、零售商的销售努力g和制造商的回收努力s的线性函数。即D（p，q，s，g）=d-p+βq+λs+αg，其中：d为产品的市场占有量，令d>p>1.需求函数表明：产品的需求与价格成反比，与质量和努力水平成正比，顾客更倾向于支付更高的价格购买高质量和服务的产品。

6）假设销售商和零售商两者都是风险中性的和以各自利润最大化的决策者，且双方拥有的信息是完全对称的[6，11，15]。

通过以上基本假设，我们可以得到制造商和零售商以及整个闭环供应链系统的利润函数分别为

2 模型的分析和求解

主要分析了集中决策和3种不同渠道权力结构下分散的闭环供应链模型。分别为：制造商Stackelberg（MS）、零售商Stackelberg（RS）、垂直的Nash（VN）3种。

2.1 集中决策模型（C）

在集中决策闭环供应链系统中，假设制造商和零售商构成一个整体联合决策闭环供应链系统的最优零售价格p*C、最优的产品质量q*C、最优的销售努力g*C和回收努力s*C使整个系统利润最大化。此时，集中决策闭环供应链模型的最优目标函数如下

引理1：当

c1c2>（λ+cδ）2c1+β2c2>α2c1

成立时，闭环供应链系统利润函数sc是关于决策变量集（p，q，s，g）的联合可微凹函数，目标利润函数存在最大值。

证明：闭环供应链系统利润函数sc关于决策变量集（p，q，s，g）的黑塞矩阵为

2.2 制造商Stackelberg决策模型（MS）

在MS模型中，制造商是Stackelberg的领导者，零售商是Stackelberg的追随者。首先制造商决定产品的单位批发价格ω、产品质量q和回收努力s；然后销售商以此为基础决定产品的单位产品的销售利润t和销售努力g.例如，电子行业，产品回收活动由设备制造商管理和制造新产品。此时，制造商Stackelberg决策模型的最优目标函数如下：

2.4 垂直Nash决策模型（VN）

在VN模型中，制造商和零售商都不是Stackelberg的领导者，两者同时独立决策。制造商决定产品的单位批发价格ω、产品质量q和回收努力s；销售商同时定产品的单位产品的销售利润t和销售努力g.垂直Nash决策模型的最优目标函数如下

2.5 4种决策模式下闭环供应链系统的对比分析

在满足条件1的前提下，对比4种决策模式下闭环供应链系统的最优决策可得以下结论。

结论1：集中决策下，整个闭环供应链系统的利润最大，并以最低的价格销售高质量的产品并提供最佳的服务努力（销售努力和回收努力）。

结论2：制造商提供最优的产品质量、最优回收努力，零售商提供的最优销售努力以及整个闭环供应链系统再制造产品的回收率和产品的需求量满足

3 闭环供应链系统的协调（S）

根据以上结论可知，闭环供应链系统在分散决策下，存在“双重边际化”影响，不能实现整个闭环供应链系统的协调。相比分散决策而言，集中决策闭环供应链系统的产品销售价格是最低的，产品质量以及服务是最优的。因此，运用改进的转售价格维持（RPM）来协调优化整个闭环供应链系统的利润。即由零售商选择以最低的价格销售产品（ω，p*C，q*C，s*C，g*C），同时向制造商收取一个固定费用F，它的大小由零售商和制造商双方讨价还价商议决定，同时必须保证双方各自的利润都不得低于各自保留的受益额，即分散决策时制造商和零售商的利润。二部定价契约的闭环供应链系统的目标利润函分别为

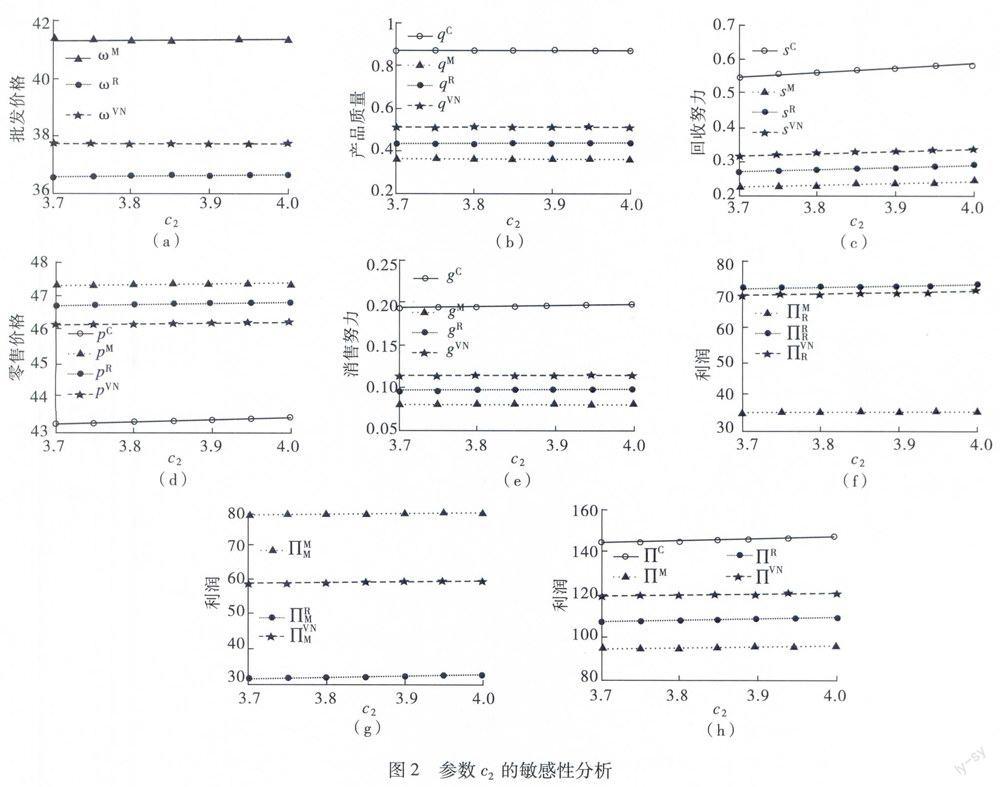
4 数值算例与灵敏度分析

为验证模型和相关结论的正确性，以及探讨不同权力结构下协调的闭环供应链的有效性。假设模型中的满足基本条件且有效的产品参数值为d=50；α=2；β=6；λ=4；δ=0.2；cm=30；cr=15；A=5；c1=100；c2=150.

分别计算不同权力结构下，闭环供应链系统的各方决策及利润（见表2）。

由图1可以看出，对闭环供应链系统的最优解集的影响，销售努力敏感性系数α和质量敏感性系数β与回收努力敏感性系数λ相似。随着回收努力敏感性系数λ的增大，产品的需求量将会增加；同时制造商将会付出更多的回收努力以扩大产品的需求和旧产品的回收量，间接提高了产品的批发价格和产品的质量水平，从而获取更多的利润。对于零售商而言，产品的销售价格随着批发价格上涨，产品的需求量增大间接地影响了零售商的销售努力水平。销售努力敏感性系数α增大无论对制造商个体，还是对整个闭环供应链系统而言都是有利的。

由图2可以看出，对闭环供应链系统的最优解集的影响，质量成本系数c1和回收努力系数c2相似。随着c2的增大，制造商和零售商的总利润都将减少。出于节省成本的目的，制造商将减少旧产品的回收努力程度，同时，零售商也会减少产品的销售努力程度。因此产品的需求将会减少。随着产品需求的减少和产能的过剩，制造商和零售商将会打折促销产品以期收回成本。无论从制造商还是零售商角度考虑，通过技术创新、广告或者其他有利的措施降低努力成本系数可获取更大的利润。

5 结 论

构建了由一个制造商和一个零售商组成的闭环供应链系统。其中制造商制造新产品和回收旧产品用于再制造并将产品批发给零售商销售。假设产品的需求函数与产品的销售价格、产品的质量水平、制造商的回收努力和零售商的销售努力成线性关系，运用博弈论分析了集中决策模型和3种分散决策模型（制造商Stackelberg（MS）、零售商Stackelberg（RS）、垂直的Nash（VN））的最优策略，并对4种模型的最优策略进行了对比分析，发现集中决策模型的决策集是4种决策模型中最优的；分散决策容易出现边际化，降低闭环供应链系统的性能；对比分析3种分散决策模型，在VN模型中，整个闭环供应链系统的利润是最大的。提出了闭环供应链在不同权力结构下实现链内协调的制造商和零售商费用补贴契约。最后通过数值仿真验证了研究构建的闭环供应链模型的合理性和不同权力结构下协调合同的有效性，灵敏度分析表明：制造商和零售商的利润与销售努力敏感性系数α、质量敏感性系数β和回收努力敏感性系数λ正相关、与质量成本系数c1和回收努力或销售努力成本系数c2负相关。研究假定在产品需求确定的基础上，制造商直接回收旧产品。未来可以结合产品需求不确定、新产品和再制造产品质量有差异、消费者异质性购买需求以及销售渠道竞争等复杂方面进一步展开研究。

参考文献：

[1] 易余胤，梁家密.奖惩机制下的闭环供应链混合回收模式[J].计算机集成制造系统，2014（1）：215-223.

[2] 熊中楷，曹 俊，刘克俊.基于动态博弈的闭环供应链回收质量控制研究[J].中国管理科学，2007（4）：42-50.

[3] 王文宾，达庆利.奖惩机制下闭环供应链的决策与协调[J].中国管理科学，2011（1）：36-41.

[4] Teunter R H，Flapper S D P.Optimal core acquisition and remanufacturing policies under uncertain core quality fractions[J].European Journal of Operational Research，2011，210（2）：241-248.

[5] 谢家平，迟琳娜，梁 玲.基于产品质量内生的制造/再制造最优生产决策[J].管理科学学报，2012（8）：12-23.

[6] 肖 迪，潘可文.基于收益共享契约的供应链质量控制与协调机制[J].中国管理科学，2012（4）：67-73.

[7] 景 熠，王 旭，李文川，等.分散决策下考虑异质需求的闭环供应链差异定价[J].计算机集成制造系统，2014（7）：1 783-1 792.

[8] 聂佳佳，邓东方.再制造产品质量对闭环供应链回收渠道的影响[J].工业工程与管理，2014（1）：1-7.

[9]Maiti T，Giri B C.A closed loop supply chain under retail price and product quality dependent demand[J].Journal of Manufacturing Systems，2014（37）：624-637.

[10]王文宾，达庆利，聂 锐.考虑渠道权力结构的闭环供应链定价与协调[J].中国管理科学，2011（5）：29-36.

[11]聂佳佳.渠道结构对第三方负责回收闭环供应链的影响[J].管理工程报，2012（3）：151-158.

[12]Fan L，Friesz T L，Yao T，et al.Strategic pricing and production planning using a Stackelberg differential game with unknown demand parameters[J].Engineering Management，IEEE Transactions on，2013，60（3）：581-591.

[13]Hong X，Wang Z，Wang D，et al.Decision models of closed-loop supply chain with remanufacturing under hybrid dual-channel collection[J].The International Journal of Advanced Manufacturing Technology，2013，68（5-8）：1 851-1 865.

[14]Chuang C H，Wang C X，Zhao Y.Closed-loop supply chain models for a high-tech product under alternative reverse channel and collection cost structures[J].International Journal of Production Economics，2014，156（5）：108-123.

[15]高举红，韩红帅，侯丽婷，等.考虑产品绿色度和销售努力的零售商主导型闭环供应链决策研究[J].管理评论，2015（4）：187-196.

[16]Gao J，Han H，Hou L，et al.Pricing and effort decisions in a closed-loop supply chain under different channel power structures[J].Journal of Cleaner Production，2015（112）：2 043-2 057.

[17]Gurnani H，Erkoc M.Supply contracts in manufacturer retailer interactions with manufacturer-quality and retailer effort-induced demand[J].Nav Res Logist，2008，55（3）：20 017.

[18]张汉江，甘 兴，赖明勇.最优价格与回收努力激励的闭环供应链协调[J].系统工程学报，2015（2）：201-209.