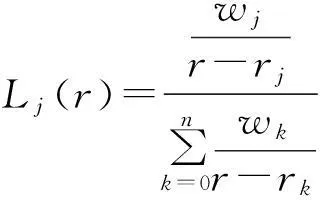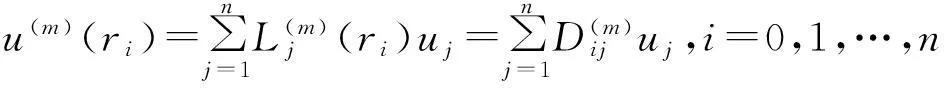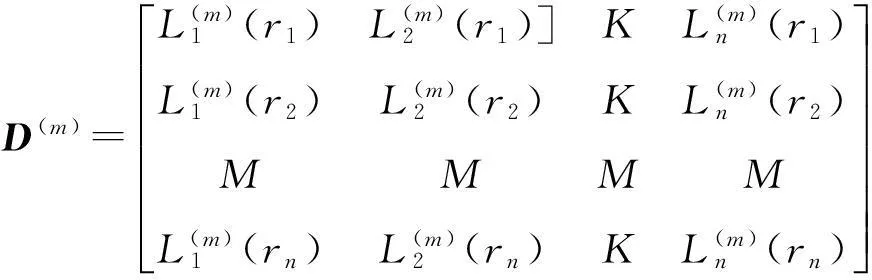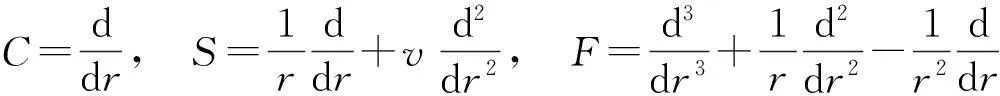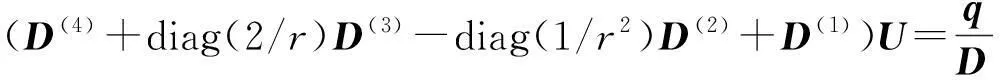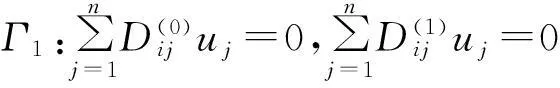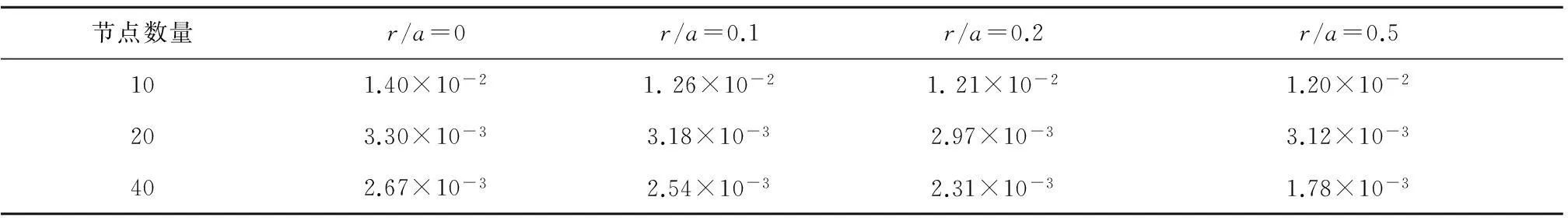极坐标下薄板弯曲问题的重心有理插值法
庄美玲,王兆清,张磊,纪思源
(山东建筑大学力学研究所,山东 济南 250101)
极坐标下薄板弯曲问题的重心有理插值法
庄美玲,王兆清*,张磊,纪思源
(山东建筑大学力学研究所,山东 济南 250101)
摘要:利用重心有理插值配点法(BRICM)研究了极坐标下薄板的弯曲问题,该方法是以重心有理插值近似未知函数强迫微分方程在离散节点处成立,得到微分方程的离散代数方程组,进而采用重心有理插值的微分矩阵将离散代数方程组表达为矩阵的形式。利用置换法施加边界条件,求解微分方程组。数值算例结果表明,该方法在解决极坐标下薄板弯曲问题上公式简单,程序实施方便且计算精度高。
关键词:极坐标;弯曲问题;重心有理插值;双调和方程;边界值
板是工程中一种常见构件,广泛应用于土木工程、机械工程和航天航空结构等领域。轴对称薄板常见于喷嘴盖、压力容器的底部、泵膜片、涡轮盘、潜艇舱壁和飞机等诸多结构中,因此,轴对称薄板[1]的研究很具有工程意义。工程实验是极其费钱、费力又费时的,而且很多工程中的设计几乎不能通过解析方法求解,因此需要一种高精度的数值方法来分析板的弯曲问题。目前, 重心有理插值配点法(BRICM)已经运用到极坐标下不规则区域的研究[2],因此对于轴对称薄板的弯曲问题,BRICM在工程研究中提供了一种高效且具有学科前沿性的数值方法。采用BRICM研究均匀、各向同性的弹性板在载荷作用下的弯曲问题[3],其数值模型是双调和方程的边值问题,可根据板的轴对称特性,化简双调和方程,施加边界条件,并求解方程。
目前,关于板的弯曲变形问题的求解方法主要有有限差分法、有限元法、边界元法、无网格法、微分求积法、傅里叶微分求积法及摄动法(HPM)等。有限差分法[4]将偏微分方程直接转化成代数方程组,是一种离散近似的计算方法,若想得到高精度计算结果就需要采用很小的计算步长,增加了计算量,降低了计算效率。有限元法[5-6]是数值算法中的一种重要的分析方法,有限元法的基本求解思想是把计算区域划分为有限个独立的单元,在每一个单元内寻找适合微分函数插值点的节点。利用多项式构造插值函数有限元方法虽然在应用数学、计算力学和工程领域得到了广泛应用,但是随着科技进步、研究工程越来越大,其缺点就日益显现。有限元法缺点有:(1)前处理比较复杂;(2)如果需要更高精度则需要划分更加细密的网格,这样就增加了工程计算量,降低工作效率;(3)对单元形状有要求,如四边形。边界元法[7]缺点是依赖于基本解,对于某些没有基本解的工程问题就不能使用。无网格法[8]只需节点信息而不需单元信息。目前流行的无网格法以滑动最小二乘法所产生的光滑函数近似函数,通过微分方程得出所求解问题的代数方程。无网格法的计算量很大,而且由于近似函数不通过节点变量值,因此要满足本质边界条件和材料不连续条件就比较困难。微分求积法[9]主要应用到非线性分析和多维领域,用较少的量得出需要的高精度结果。但是目前该方法对不规则区域很难求解,对于大量节点具有不稳定性。傅里叶微分求积法[9]求解的工作量很大。摄动法(HPM)[10]又称小参数展开法,借助于选定的并且具有精确解的微分方程组,用来近似求解微分方程。
上述几种方法虽然可以解决板的弯曲问题,但是缺少灵活性且精度较低。本文采用BRICM求解极坐标下轴对称板的弯曲问题,利用板轴对称的特性,将二维问题转化为一维问题,大大减少了工作量,节省了时间,提高了工作效率。通过与摄动法(HPM)、无网格法和有限元法的比较发现,重心有理插值方法计算公式简单,程序实施方便,计算精度极高[11-13]。
1重心有理插值及其微分矩阵
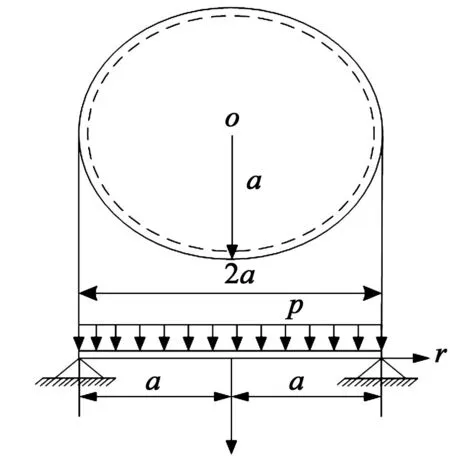
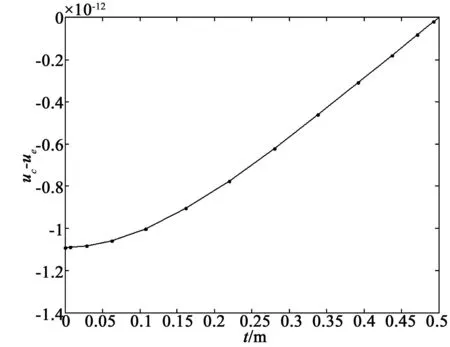
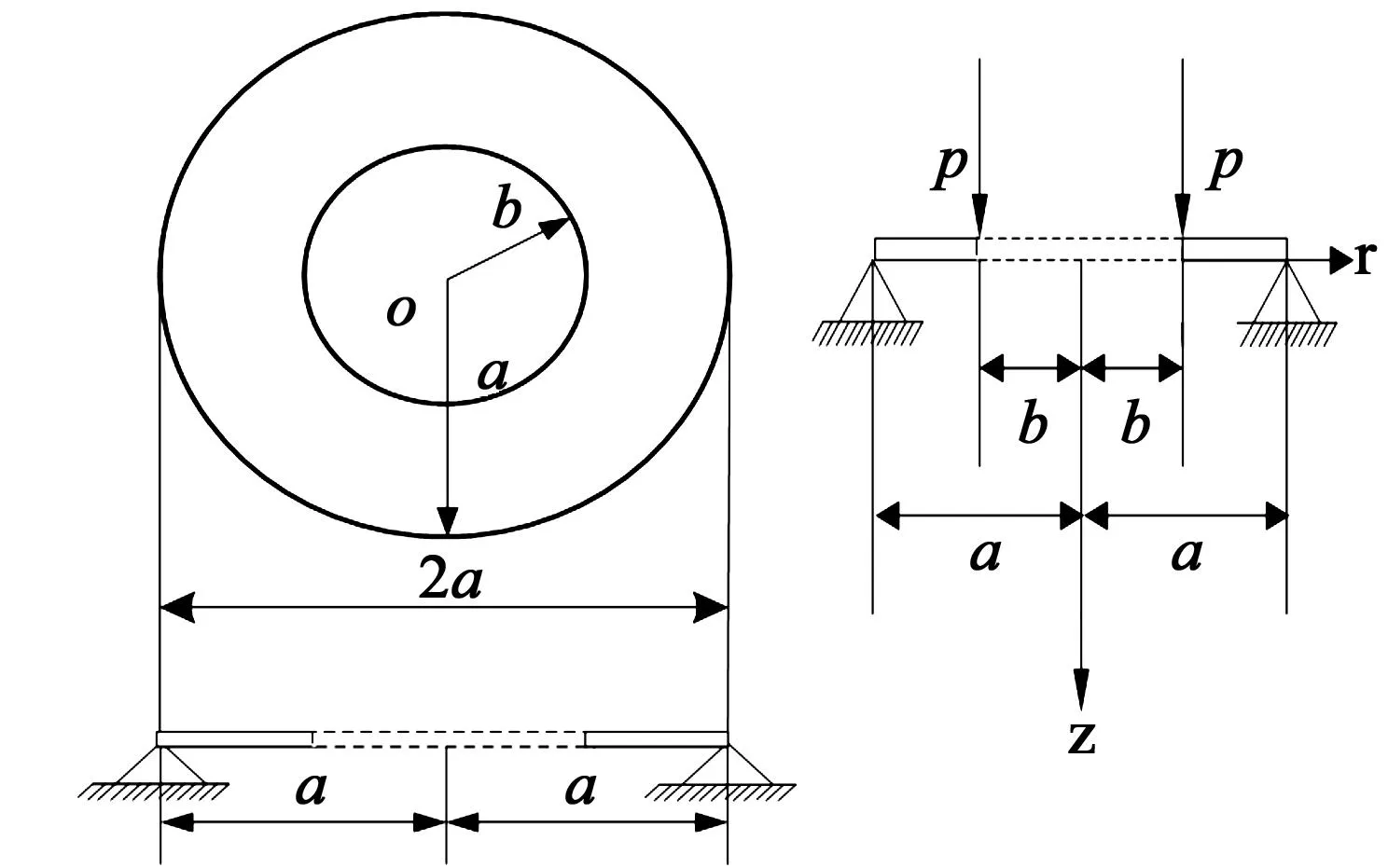
考虑定义在区间[a,b]上的函数u(r),函数u(r)在节点a=r1 (1) 其中,wj称为插值权且j=0,1,…,n,指标集Jj={i∈I:j-d≤i≤j},d=1,2,…,n。记重心有理插值的插值基函数为 (2) 函数u(r)的重心有理插值可表示为 (3) 则函数u(r)的m阶导数可表示为 (4) 函数u(r)在节点x1,x2,L,xn处的m阶导数可表示为 (5) u(m)=D(m)u, (6) 公式中, u(m)=[u1(m),u2(m),…,un(m)]T为未知函数u(r)在节点处的m阶导数值列向量,矩阵D(m)称为未知函数的m阶重心插值微分矩阵,其元素为Dijm=Lj(m)(ri),u=[u1,u2,…,un]T为未知函数在节点处的函数值。一阶微分矩阵由公式(2)直接求导得到,高阶微分矩阵可由递推公式计算[14]。 2极坐标下对称薄板弯曲问题的BRICM 极坐标下板弯曲的控制方程为[15]: (7) 其展开式为 (8) 其中,u=u(r)为未知的板弯曲的挠度,q为均布荷载,D=Et3/12(1-v2)为弯曲刚度,E是弹性模量,t是板的厚度,v是泊松比。 极坐标下板的边界条件包括固支、简支和自由边,分别用Γ1,Γ2和Γ3表示,所以轴对称薄板的区域Ω的边界为Γ=∂Ω=Γ1∪Γ2∪Γ3, 且边界条件如下 (9) 其中,hi=0,i=1,2,3,4;C,S,F分别定义为 (10) 由公式(6)得方程(7)的重心有理插值计算格式为 (11) 式中,U=[u11,u12,…,u1n,u21,u22,…,u2n,…,un1,un2,…,unn,]T,q=[q1,q2,…,qn]。 D(1)、D(2)、D(3)、D(4)其边界的离散形式是分别为挠度u关于r在节点rj(j=1,2,…,n)处的一阶、二阶、三阶、四阶微分矩阵。 由公式(5)得到公式(9)的BRICM离散格式为 (12) 公式(12)可以进一步改写为微分矩阵形式 Γ1:B0U=0,B1U=0, Γ2:B0U=0,B2U=0, Γ3:B2U=0,B3U=0。 (13) 利用置换法施加边界条件,由公式(11)和公式(13)得到极坐标下板在固支(a),简支(b)和自由边(c)的重心插值离散矩阵表示如下: (14) 图1 均布载荷作用下的简支圆板受力图Fig.1Force diagram of round plate with clamped edge for a uniform load 3数值结果 为了表明该方法在解决极坐标下薄板弯曲问题的有效性和计算精度,本文给出了2个数值算例[15-16]。数值算例程序由MATLAB 编写,采用BRICM,所用节点为Chebyshe节点,求出数值解与解析解进行比较,绝对误差Ea=‖uc-ue‖2,相对误差Er=‖uc-ue‖2/‖ue‖2其中uc,ue分别为函数的数值计算值和解析解值列向量,‖·‖2为向量的2范数。 算例1简支圆板在均布载荷作用下(图1) 计算区域Ω=[0,5],在r方向取11个计算节点,边界条件为公式(12)中Γ2且Γ2中uj=u(rj=5),j=1,2,…,11,利用置换法施加边界条件,求解方程组(14)中(a)得到板弯曲的挠度数值解。图2为算例1 利用BRICM、 HPM[10]与解析解(EXACT)的挠度结果图,图3为BRICM与解析解的挠度绝对误差结果图。 图2 算例1 BRICM 、HPM与EXACT挠度结果图Fig.2 Results illustration of BRICM, HPM and EXACT of deflection for instance 1 图3 算例1 BRICM与EXACT挠度绝对误差结果图Fig.3 Results illustration of BRICM and EXACT of absolute errors of deflection for instance 1 由文献[10]中的图3(有限元法、HPM与EXACT的对比)分析可知,有限元法求出的数值精度低, HPM求出的近似解与EXACT高度吻合;由本文图2可知,HPM求出的近似解与BRICM求出的结果均与EXACT高度吻合。由本文图3可知BRICM的绝对误差精度高达10-12。 本文表1为文献[16]利用无网格法在不同r/a取值情况下简支圆板的相对误差,采用BRICM计算的相对误差与文献[16]中当r/a=0.5时的计算精度的对比分析列于表2,同时利用有限元分析时取16个计算单元得到的误差也列于表2中。 表1 无网格法计算的简支圆板挠度的相对误差 表2 算例1不同计算方法不同计算节点下板挠度的相对误差 由表1和表2数据可知,有限元的计算精度为10-2,无网格法的最好计算精度达到10-3,BRICM的计算精度高达10-11。 算例2简支环形板内边缘受线性载荷作用(图4) 弹性模量E=2.0×107N/m2,外半径a=0.8 m,内半径b=0.6 m,板厚t=0.06 m, 泊松比v=0.3,弯曲刚度D=Et3/12(1-v2),p=1.0×103N,解析解如下: 计算区域Ω=[0.6,0.8],在r方向取n个计算节点,边界条件为公式(12)中Γ2,且Γ2中:(1)uj=u(rj=0.6),(2)uj=u(rj=0.8),j=1,2,…,n,利用置换法施加边界条件,求解方程组(14)中(b)得到板弯曲的挠度数值解。 不同数量n个Chebyshev计算节点条件下,BRICM计算的绝对误差和相对误差列于表 3 中。 由表3可知,随着节点数量的增加,其误差计算精度稳定在10-8。 图4 简支环形板内边缘受线性载荷作用Fig.4 Illustration of inner edge of simply supported annular plate forced by a uniformly distributed linear load 挠度BRICM绝对误差Ea相对误差Er114.6455×10-87.84011×0-8u152.8813×10-104.2069×10-10178.4742×10-101.1679×10-8214.9487×10-86.1800×10-8 4结论 (1)由板的边界条件和极坐标下板弯曲的控制方程,采用BRICM将其离散,利用置换法施加边界条件,利用MATLAB编写程序,求解微分方程组,得到板的弯曲挠度数值解。其计算公式简单,利用MATLAB编制的计算程序有效可靠,可供广大工程设计人员使用。 (2)由数值算例分析可知,计算精度高达10-8,随着节点数量的增加,其误差计算精度稳定在10-7与10-9之间。有限元的最好计算精度可达10-2,但其计算精度依赖于网格的细化量,大大增加了工作量。而该方法公式简单,既不需要画网格,也不需要通过坐标转换将不规则区域转换为规则区域。该方法为工程中板弯曲问题提供了一种高精度无网格解法 ,值得推广运用到不规则板问题和其他需要高精度的工程问题中。 参考文献: [1]DESHMUKH K C, WARBHE S D, KULKARNI V S. Quasi-static thermal deflection of a thin clamped circular plate due to heat generation[J]. Journal of Thermal Stresses, 2009, 32(9):877-886. [2]WANG Z Q, LI S C, Ping Y, et al. A highly accurate regular domain collocation method for solving potential problems in the irregular doubly connected domains[J]. Mathematical Problems in Engineering, 2014 (1):1-9. [3]MOHYUD-DIN S T, YILDIRIM A, HOSSEINI M M. An iterative algorithm for fifth-order boundary value problems[J]. World Applied Sciences Journal, 2010(5):531-535 [4]VIRDI K S. Finite difference method for nonliear analysis of structures[J]. Journal of Constructional Steel Research, 2006, 62(11): 1210-1218. [5]KWON Y W, BANG H. The finite element method using MATLAB[M]. Boca Raton, FL, USA: CRC Press, Inc.1996. [6]TANAKA M, MATSUMOTO T, OIDA S. A boundary element method applied to the elastostatic bending problem of beam-stiffened plates[J]. Engineering Analysis with Boundary Elements, 2000, 24(10): 751-758. [7]DONNING BM, LIU WK. Meshless methods for shear-deformable beams and plates[J]. Computer Methods in Applied Mechanics and Engineering, 1998, 152(1/2): 47-71. [8]WANG X, BERT CW, STRIZ AG. Differential quadrature analysis of deflection,buckling,and free vibration of beams and rectangular plates[J]. Computers & Structures, 1993, 48(3): 473-479. [9]SHAO W, WU X. Fourier differential quadrature method for irregular thin plate bending problems on Winkler foundation[J]. Engineering Analysis with Boundary Elements, 2011, 35(35):389-394. [10]ROSTAMIYAN Y, FEREIDOON A, DAVOUDABADI M R, et al. Anzlytical approach to investigation of deflection of circular plate under uniforn load by homotopy load by homotopy perturbation method [J]. Mathematical and Computational Applications, 2010, 15( 5):816-821. [11]马燕, 王兆清, 唐炳涛. 波动问题的高精度重心有理插值配点法[J]. 山东科学, 2012, 25(3): 80-87. [12]王兆清,綦甲帅,唐炳涛. 奇异源项问题的重心插值数值解[J]. 计算物理,2011,28(6): 883-888. [13]綦甲帅,王兆清. 重心插值Galerkin法求解梁弯曲变形问题[J]. 山东科学,2013,26(3): 60-65. [14]李树忱,王兆清. 高精度无网格重心插值配点法—算法、程序及工程应用[M]. 北京:科学出版社,2012. [15]VENTSEL E, KRAUTHAMMER T. Thin plates and shells: Theory, Analysis and Applications [M]. USA :CRC Press,2001. [16]NG T Y, LI H,CHENG J Q, et al. A novel true meshless numerical technique (hM-DOR method) for the deformation control of circular plates integrated with piezoelectric sensors/actuators[J].Smart Materials & Structures, 2003, 12(6):955-961. Barycentric rational interpolation collocation method for bending problem of a thin plate in polar coordinates ZHUANG Mei-ling, WANG Zhao-qing*,ZHANG Lei, JI Si-yuan (Institute of Mechanics, Shandong Jianzhu University, Jinan 250101, China) Abstract∶We apply barycentric rational interpolation collocation method (BRICM) to the bending problem of a thin plate in polar coordinates. It approximates an unknown function with barycentric rational interpolation by compelling a biharmonic equation to equal to the unknown function at discrete nodes, and acquires the discrete algebraic equations of the biharmonic equation. It further denotes the discrete algebraic equations as a matrix by the differential matrix of barycentric rational interpolation. It eventually solves the differential equations with a boundary conditions mixed replacement method. Numerical instances demonstrate that the method has simple calculation formulae for bending problem of a thin plate in polar coordinates, convenient program and high calculation precision. Key words∶polar coordinate; bending problem; barycentric rational interpolation method; biharmonic equation; boundary value problem 中图分类号:O241 文献标识码:A 文章编号:1002-4026(2016)02-0082-06 作者简介:庄美玲(1989-), 女,硕士研究生,研究方向为工程数值方法。Email:18036558037@163.com*通讯作者,王兆清(1965-), 男,副教授,博士,研究方向为工程数值方法。Email:sdjzuwang@gmail.com 基金项目:国家自然科学基金(51379113) 收稿日期:2015-04-05 DOI:10.3976/j.issn.1002-4026.2016.02.015