一种并行结构有符号乘累加器的设计

张琳， 田现忠,2 ，赵兴文 ，颜广 ，葛兆斌

(1． 山东省科学院自动化研究所，山东 济南 250014；2．吉林大学仪器科学与电气工程学院，吉林 长春 130026)



一种并行结构有符号乘累加器的设计

张琳1， 田现忠1,2，赵兴文1，颜广1，葛兆斌1

(1． 山东省科学院自动化研究所，山东 济南 250014；2．吉林大学仪器科学与电气工程学院，吉林 长春 130026)

摘要：本文采用补码分布式算法，简化了有符号数、无符号数以及混合符号数的乘加减运算，通过改进累加器树结构、全加器逻辑电路，设计了一种新型乘累加器结构。通过Altera公司的EP1C3T144C8实现了该乘累加器6个9位有符号操作数的乘累加运算的功能和时序仿真,结果证明了该算法的有效性。该设计解决了常规DA分布式算法系数不能更新和占用大量RAM资源的缺点，可以应用到数字滤波器设计中，也可以作为快速的运算单元应用到DSP数字信号处理器中。

关键词：乘累加器；有符号数；可变系数

乘累加器是信号处理当中的基本运算单元，是fir滤波器和自适应滤波器的主要结构，其速度和占用芯片资源的多少是影响数字硬件实现的关键性因素[1]。乘累加器主要分为迭代、线性阵列和并行结构，早期采用迭代结构使用软件实现乘法操作，后来逐渐发展成设计专用的硬件乘累加器，以获得更高的性能。目前高性能的乘法操作都是采用硬件实现的乘累加器，而且多是采用并行结构[2]。目前国内外并行乘累加器的算法主要有Booth算法和Wallace树，当前流行的部分积产生算法就是在Booth算法的基础上改进的。虽然改进的Booth算法可以减少部分积的数量，减少了硬件开销且提高了电路性能，但是当阶数比较高的时候，Booth算法的编码逻辑却能带来显著的资源开销。Wallace树开辟了并行结构的先河，与传统算法相比，基于Wallace树的分布式算法可极大地减少硬件电路规模，很容易实现流水线处理，提高电路的执行速度，而且不受器件的限制[3]。 为了克服现有乘累加器的不足，同时为即将研制的通用数字神经处理器MCU提供一个高速的运算单元，本文对乘累加器算法进行了改进，采用补码的分布式算法并在硬件电路上得以实现。

1补码的分布式算法

分布式算法(distributed arithmetic, DA)与传统算法实现乘加运算的不同在于执行部分积运算的先后顺序不同[4]。分布式算法在完成乘加功能时是通过将各输入数据每一对应位产生的积预先进行相加形成相应部分积，然后再对各部分积进行累加形成最终结果，而传统算法是等到所有乘积产生之后再进行相加来完成乘加运算的。因为大多数的乘累加过程会涉及到有符号数的运算，所以这里的乘累加器所针对的操作数统一采用补码。采用补码运算在进行加法运算的时候不需要考虑操作数的正负，也不需要对结果进行转换，直接使用全加器就可以得到正确的结果。所以说补码的分布式算法简化了有符号数、无符号数以及混合符号数的乘加减运算，可以使加法树在有符号的多操作树累加中得到应用，同样时延更小的华莱士树也可以在这里使用，可以进一步提高运算的速度[5-12]。补码乘运算规则：

(1)当被乘数为任意整数，乘数为正整数时

被乘数{x}补=x0·x1x2…xn=2n+1+x，

乘数{y}补=0·y1y2…yn(y≥1)，

{x}补{y}补=x0·x1x2…xn×0·y1y2…yn

=(2n+1+x)×y

=2n+1×y+xy(mod 2n+1)

=2n+1+xy

={xy}补。

(1)

此时乘积的结果就等于x与y的补码直接相乘。

(2)当被乘数为任意整数，乘数为负整数时

被乘数{x}补=x0·x1x2…xn，

乘数{y}补=1·y1y2…yn=2n+1+y，

y={y}补-2n+1

=1·y1y2…yn-2n+1

=0·y1y2…yn+2n-2n+1

=0·y1y2…yn-2n,

xy=x(0·y1y2…yn)-2n×x,

{xy}补={x}补(0·y1y2…yn)+{-x}补×2n。

(2)

当乘数为负数时，补码的乘积结果等于x的补码与y的补码去掉符号位后的乘积-x的补码乘以最高位(符号位)。

由此可以获得定点补码乘法的统一公式为

{xy}={x}补×(0·y1y2…yn)+{-x}补×2n×y0，

(3)

其中-x的补码由x的取反加1得到

(3)分布式算法

考虑如下的乘积项：

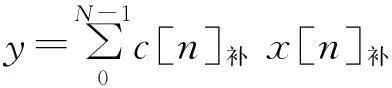
c,x为有符号数时，表达式如下

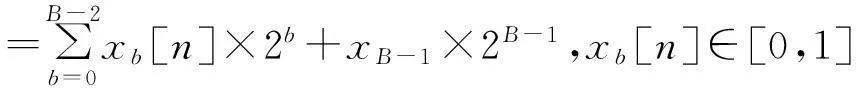
最高位xB为符号位，xb表示x的第b位，乘积y可以表示为

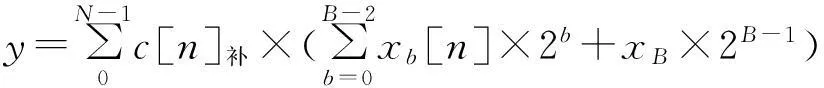
重新分别求和，并考虑补码乘法规则结果如下

y=c[0]补(xB-2[0]2B-2+xB-3[0]2B-3+…+x0[0]20)+{-c[0]}补xB-1[0]2B-1+

c[1]补(xB-2[1]2B-2+xB-3[1]2B-3+…+x0[1]20)+{-c[1]}补xB-1[1]2B-1+…+

c[N-1]补(xB-2[N-1]2B-2+xB-3[N-1]2B-3+…+x0[N-1]20)+{-c[N-1]}补xB-1[N-1]2B-1

=(c[0]xB-2[0]+c[1]xB-2[1]+…+c[N-1]xB-2[N-1])2B-2+

(c[0]xB-3[0]+c[1]xB-3[1]+…+c[N-1]xB-3[N-1])2B-3+…+

(c[0]x0[0]+c[1]x0[1]+……+c[N-1]x0[N-1])20+({-c[0]}补xB-1[0]+

{-c[1]}补xB-1[1]+…+{-c[N-1]}补xB-1[N-1])2B-1。

(4)

分布式算法硬件结构如图1所示。

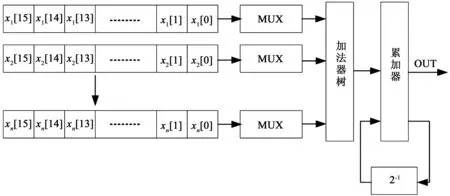
图1　分布式结构Fig.1　Structure of a distributed algorithm

另外，为了追求更快的运算速度，我们采用并行算法对乘积项进行处理，每次可令操作数移动2～3位，可以进一步地提高运算的速度，但是结构也相应的要复杂很多。当同时移动3位时，新的系数c[n]将通过下面表1的规则获得。

表1　系数规则

加法器树也可以采用华莱士树代替，可以进一步减小加法器的进位延时。

2仿真结果与分析

2.1仿真结果

采用Altera公司的Cyclone EP1C3作为目标器件，用Verlog HDL描述了整个设计，并在Quartus开发系统中完成了整个设计的输入、功能仿真和时序仿真，最后生成编程文件。乘累加器的目标器件EP1C3T144C8的工作频率为101.9 4 MHz，逻辑单元占总资源的2%，所用的引脚数占总引脚数的23%，我们通过6个乘积项9位有符号数的乘累加在目标器件上进行算法的验证。

当x和系数c的取值分别取以下值时，最终乘累加器的计算结果为-58 600,得到了正确的结果，说明该乘累加器的设计是正确的。

x1=100;x2=200;x3=30;x4=40;x5=50;x6=60;

c1=-100;c2=-200;c3=-30;c4=-40;c5=-50;c6=-60;

图2为仿真的结果。

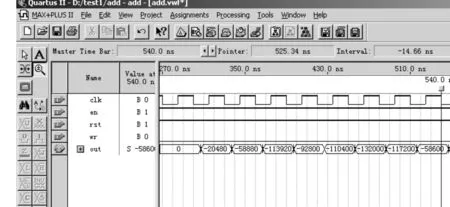
图2　乘累加器仿真结果Fig.2　Simulation results of the multiply-accumulator

2.2算法分析

对比目前的DA分布式算法和采用乘法器结构的MAC，本文的设计具有更多的优势。传统的DA分布式算法，需要根据系数c计算累加值后储存在LUT中，这样带来两个问题。第一，不能即刻更新系数c，每一次更新都需要重新计算大量的累加值，这限制了分布式算法的应用范围。第二，随着阶数(N)和数据位数的增加，LUT所需的ROM也将以2的N次方迅速地增加。采用乘法器结构的MAC，乘法器占用资源多，且即使高端FPGA内部的乘法器数量也满足不了并行运算的消耗[13-16]。而本文设计的乘累加器使用加法器树来代替原来的LUT，这样的处理可以使系数c可以随时更改数值，使得基于分布式算法的乘累加器不再局限于定系数乘累加运算，而且对FPGA内部RAM的需求也降到了0。

3结论

本文设计了一种并行结构采用补码分布式算法的乘累加器，并在EP1C3T144C8器件中实现。这种乘累加器改变了原来DA分布式算法系数固定的缺点，并且不需要大量的ROM用来作为系数表,所占用芯片的面积更小，实现了符号数的乘累加计算，扩展方便，特别适合于可编程逻辑器件的实现。该乘累加器性能先进，可以被广泛的运用到其他数字硬件设计中。但是，该乘累加器还有不少可改进之处，比如采用并行算法缩短运算周期，利用Wallace tree代替普通的加法器树等等，能够进一步地简化算法，减少延时降低功耗。

参考文献:

[1]陈杨生，颜刚锋. 硬件实现基于BP神经网络设计的带阻FIR滤波器[J]. 浙江大学学报:工学版，2006, 40(7)：1146-1149.

[2]赵宇玲. 基于FPGA的信号采集与处理系统设计与实现[D]. 南京：南京理工大学，2008.

[3]兰景宏. 高性能乘累加器的设计研究[D]. 北京： 北京大学，2005.

[4]MEYER-BAESE U.数字信号处理的 FPGA 实现[M].北京：清华大学出版社，2006.

[5]李梅，王兰勋. 分布式算法在FIR数字滤波器实现中的应用[J]. 通信技术，2008，41(8):15-16.

[6]CILETTI M D. Verlog HDL 高级数字设计[M]. 北京：电子工业出版社，2005.

[7]李勇，裘式纲，王凤学，等. 计算机原理与设计[M]. 长沙：国防科技大学出版社，1989.

[8]SUNDER S.A fast multiplier based on modified Boothalgorithm [J]. Int J Electronics,1993,75(2)：199-208.

[9]SAIT S M. A novel technique for fast multiplication [J]. Int J Electronics，1999,86(1):67-77.

[10]张禾，陈客松. 基于FPGA的稀疏矩阵向量乘的设计研究[J]. 计算机应用研究，2014, 31(6)：1756-1759.

[11]于亚萍，陈雪强，刘源，等. 基于FPGA串并结合FIR滤波器的设计[J]. 湖北农业科学，2012, 51(14)：3092-3095.

[12]邹翠，谢憬，谢鑫君. 基于高性能浮点乘累加器的浮点协处理器设计[J]. 信息技术，2014(7) : 121-124.

[13]徐琪，段哲民. 泰勒级数的DDS设计与FPGA实现[J]. 计算机工程与应用，2014, 50(5)：208-211.

[14]邓耀华，吴黎明，张力锴. 基于 FPGA 的双 DDS 任意波发生器设计与杂散噪声抑制方法[J].仪器仪表学报，2009，30(11)：2255-2261.

[15]黄丹连. 高吞吐率单双精度可配置浮点乘累加器的设计与实现[D]. 上海：上海交通大学，2011.

[16]胡少轩. 基于FPGA的MAC FIR滤波器的实现[J]. 山西焦煤科技，2011(11):44-46.

Design of a parallel signed multiply-accumulator

ZHANG Lin1,TIAN Xian-zhong1,2,ZHAO Xing-wen1,YAN Guang1,GE Zhao-bin1

(1. Institute of Automation, Shandong Academy of Sciences, Jinan 271018, China;2. School of Instrumentation & Electrical Engineering, Jilin University, Changchun 130026, China)

Abstract∶We employ complement distributed algorithm to simplify addition, subtraction and multiplication of signed number, unsigned number and the number with mixed symbols. We further design a new multiply-accumulator structure through improving tree structure of an accumulator and logic circuit of a full adder. It is implemented with EP1C3T144C8 device from Altera company. Its effectiveness is proved through multiply-accumulating functionality and timing simulation result of six nine-bit signed operands. Its design overcomes the negatives of large RAM resource occupancy and no coefficient update of conventional distributed algorithm (DA). It can therefore be applied to the design of digital filters, and digital signal processors (DSP) as a rapid compute unit.

Key words∶multiply-accumulator; signed-number; variable coefficient

中图分类号：TN431.2

文献标识码：A

文章编号：1002-4026(2016)02-0096-05

作者简介：张琳(1987-)，女，硕士，研究方向为嵌入式应用开发编程。Email：zhanglin987326@126.com

基金项目：山东省科学院先导科技专项;山东省自主创新及成果转化专项(2014CGZH1104)

收稿日期：2015-06-11

DOI:10.3976/j.issn.1002-4026.2016.02.018