机翼缘条喷丸强化变形模拟与参数优化

张 炜，刘立彬，夏明莉，王永军，肖旭东，何俊杰

（1.中航飞机西安飞机分公司，西安 710089；2.中国人民解放军驻西飞公司军事代表室，西安 710072；3.西北工业大学机电学院，西安 710072）

喷丸强化工艺广泛应用于航空航天和汽车等领域中结构件的表面处理，在喷丸强化工艺中通过高速弹丸撞击工件表面，在表层形成均匀的残余压应力，可以有效地提高工件的疲劳寿命[1-3]。

喷丸残余压应力可以阻止裂纹的萌生和发展，同时对于非对称结构件，其在均匀残余压应力的作用下会产生一定的整体变形，需要调整不同位置的喷丸强度以减小整体变形量。飞机的机翼缘条是连接飞机机翼和中央翼的重要结构件，如图1所示，呈非对称结构，制造精度要求较高，喷丸强化后会产生整体弯曲变形。

喷丸变形的直接诱因是喷丸残余应力，可以通过解析计算[4-5]、数值模拟[6-7]和试验等方法建立喷丸参数与喷丸残余应力之间的关系。喷丸试验后可以利用X射线衍射等[8-9]方法测量喷丸残余应力，结合不同喷丸参数下的残余应力测量值可以建立喷丸参数与喷丸残余应力之间的关系。

可以利用有限元模拟方法分析喷丸残余应力作用下的工件变形。为便于计算，一般采用等效模拟的方法，具体有等效热载荷法[10-11]、面内挤压法[12]及直接应力法[13-14]。Gariépy等[13]研究了大尺寸零件的喷丸变形模拟方法，通过将弹丸撞击模拟获得的平均应力场引入大尺寸零件的有限元模型中模拟零件的变形。

本文首先通过试验方法建立喷丸参数与喷丸应力场间的关系，进而通过有限元模拟的方法得到机翼缘条在不同喷丸应力场作用下的变形，从而得到与最小变形量对应的喷丸应力场，并根据喷丸参数与应力场的关系得到优化的喷丸参数，以获得最小的喷丸变形，并与机翼缘条喷丸强化的试验值进行比较。

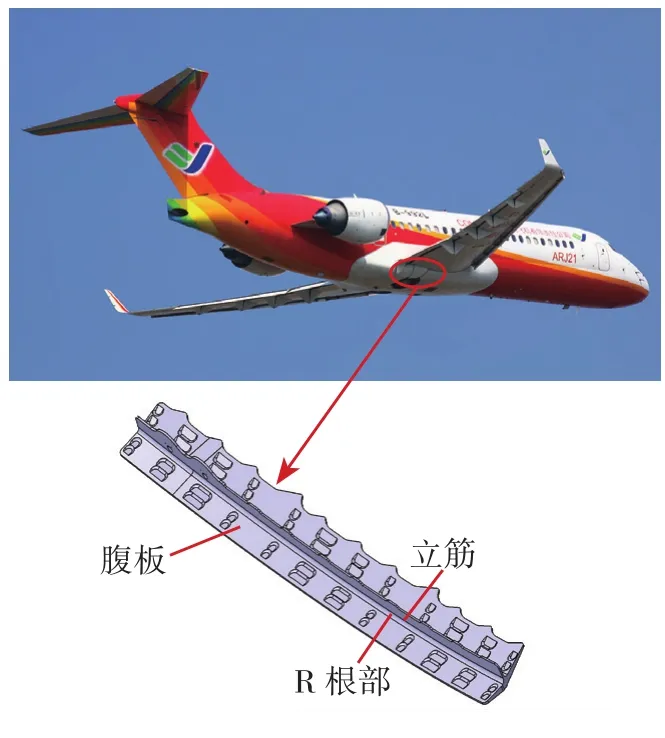
图1 某飞机下缘条零件Fig.1 Flange part of a certain type of aircraft

喷丸强化应力场

为方便喷丸应力场的计算，拟采用近似函数表征平均喷丸应力场，使近似应力场与实际喷丸应力场具有相同的成形效果。弹丸撞击产生的喷丸应力沿板料厚度方向的分布规律与余弦函数相似，如图2所示。在此将板料沿厚度方向分为喷丸应力层和弯曲变形层，在喷丸应力层中用余弦函数近似表示，在弯曲层中用线性函数近似表示，以分段函数的形式写为：

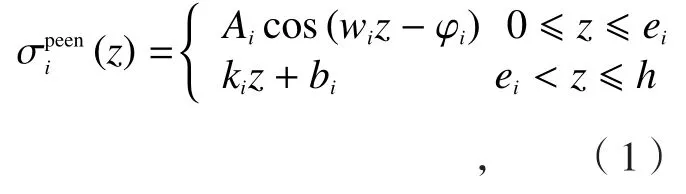
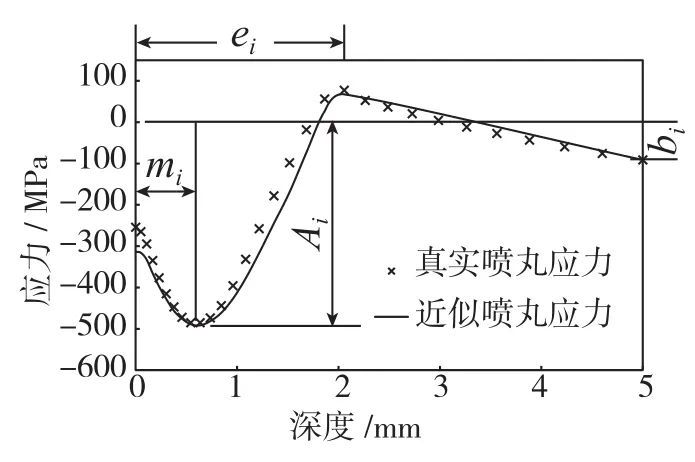
图2 余弦函数表示的喷丸诱导应力Fig.2 Shot peening induced stress expressed with cosine function

式中，Ai、ωi、φi、ki和bi为控制参数，ei表示喷丸应力层的深度，h表示板料厚度。

当利用上述近似函数表示喷丸诱导应力时，由于喷丸诱导应力对应于四周被完全约束的板料构型，弯曲层中的面内变形可以被忽略，只考虑喷丸应力层中的诱导应力，则喷丸诱导应力场可以写为：

式中，参数ωi和φi可以用压应力层的深度ei和最大压应力的位置mi表示为：

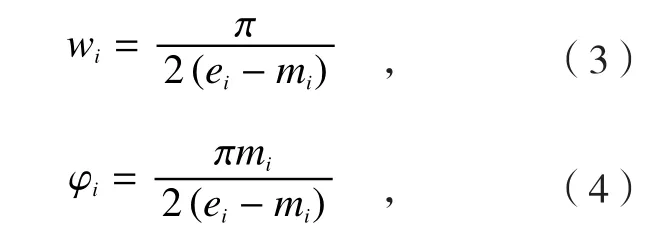
则压应力层中的诱导应力场也可以表示为：

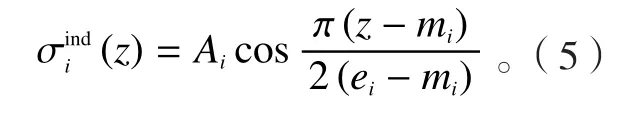
缘条喷丸变形模拟与参数优化

由于某飞机下缘条零件的几何实体外形轮廓比较复杂，为了保证计算的可行性并合理节省计算成本，方便网格划分，进行有限元模拟时，对几何模型做了适当的简化，如图3所示。采用壳单元代替实体单元进行建模，将各处的厚度赋给壳单元模型。下缘条零件结构可分为腹板、R根部及立筋3部分，如图1所示。提取腹板的上表面和立筋的侧面进行组合得到下缘条零件的壳体模型，将得到的下缘条零件的壳体模型导入ABAQUS中，腹板壳单元和立筋壳单元采用ABAQUS软件自身提供的Tie方式组合到一起。

参考Gariépy等[13]的模拟方法，采用3层结构的复合材料常规壳单元，外侧两个分层用来定义初始应力场，中间层用于调整模型的厚度，每一层设定9个辛普森积分点。

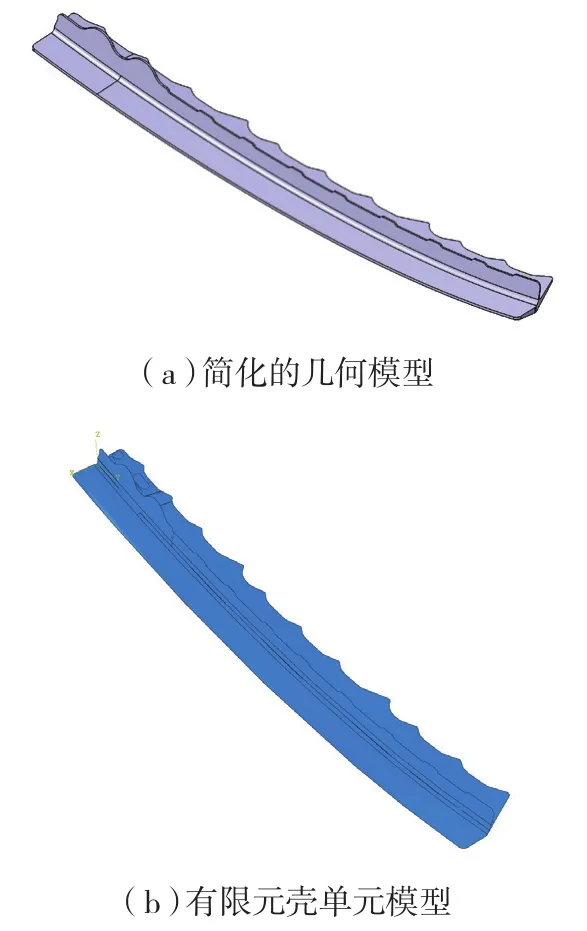
图3 机翼缘条的简化模型和有限元模型Fig.3 Simplified model and finite element model of the wing flange

该缘条的喷丸强度要求为0.15～0.25mm（A）。缘条 R根部采用固定的喷丸强度0.15mm（A），弹丸喷射角度为90°。腹板下表面、上表面及立筋表面上的喷丸强度需要进行优化组合。Box-Behnken试验设计是一种可以评价指标和因素间的非线性关系的试验设计方法。在喷丸强度的选用范围，根据Box-Behnken的中心组合试验设计原理对各因素进行3水平模拟试验设计，试验设计方案如表1所示。

喷丸试验

1 试验材料

缘条零件的材料为2026-T3511铝合金，通过单向拉伸试验获得材料室温下的力学性能，弹性模量为72.51GPa，屈服强度为 351.75MPa，抗拉强度为583.82MPa，延伸率为16.48%。

2 喷丸强化残余应力的测量

采用气动式喷丸机对缘条零件的初始毛坯料进行表面强化处理，设备型号为Pr Trat 4G7 4Sm，弹丸的规格为ASH230，机床的喷嘴直径为10mm，弹丸流量为10kg/min，喷嘴移动速度设定为800mm/min，机床喷嘴与零件表面之间的距离为500mm。在缘条零件的不同区域分别采用不同的喷丸压力和喷射角度进行喷丸强化处理，利用A型Almen 试片来监测喷丸强度，具体参数见表2。

喷丸后采用PROTO公司的iXRD组合式X射线残余应力分析仪测量试件喷丸后的残余应力，为了得到沿试件厚度方向不同深度的残余应力值，采用相应的电解抛光设备进行电解抛光剥层。X射线残余应力分析仪额定功率为300W，测试方法采用同倾法，设定测试条件，靶材为Co K α，管电压为20kV，管电流为4mA，X射线曝光时间设定为2s，曝光10次，使用1mm×3mm光缝。

表1 Box-Behnken模拟试验设计参数

表2 喷丸强化残余应力测量试件的工艺参数

3 喷丸强化变形的测量

分别将喷丸前和喷丸后缘条零件置于检验工装上（图4），利用塞尺检测缘条零件与相对应的检验工装之间的间隙，通过对比喷丸强化前后间隙变化来确定缘条的喷丸强化变形量。

图4 机翼缘条试验件Fig.4 Wing flanges for test

结果分析与讨论

1 喷丸参数与喷丸应力

利用式（5）拟合通过X射线衍射方法测得的不同喷丸参数下的喷丸残余应力，如图5所示。可以看出式（5）能较好地表达喷丸应力值沿深度方向的变化。

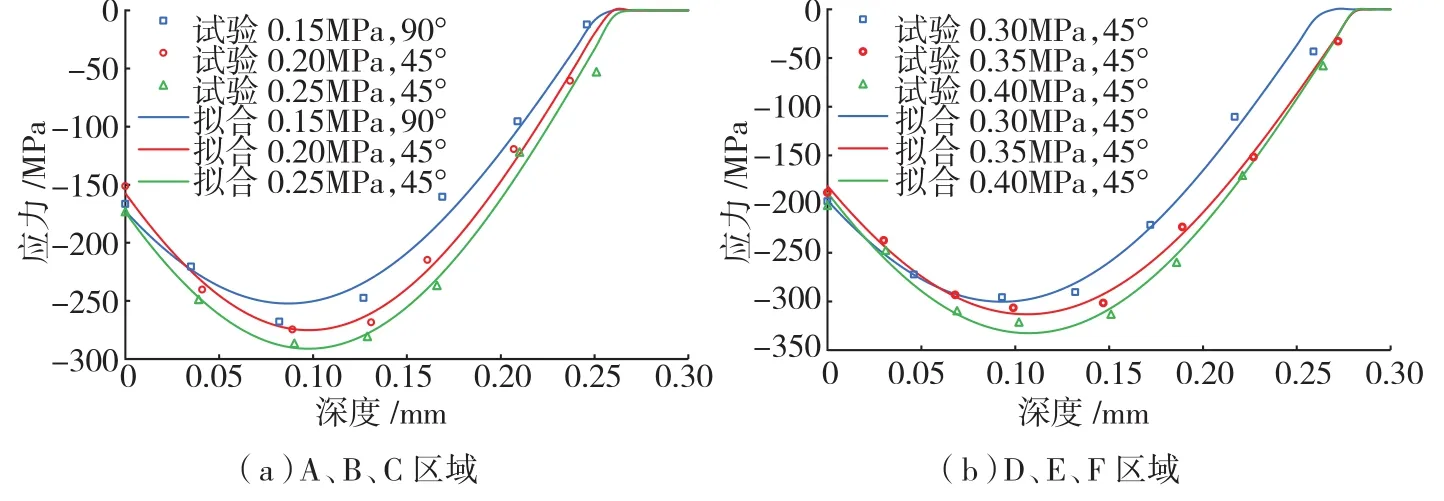
图5 不同喷丸参数下的喷丸应力场试验值与拟合值Fig.5 Experimental value and fitting value of shot peening stress field under different parameters

喷射角度为45°条件下，对拟合所得的式（5）中的参数A、e及m再次以喷丸压力P为变量进行拟合，所得关系为：

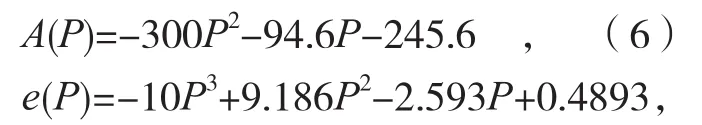
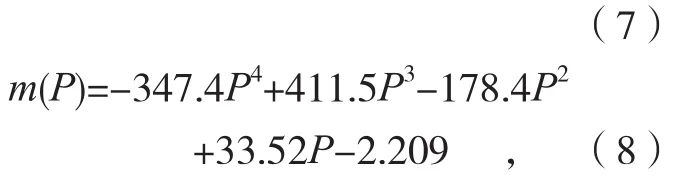
上述3个关系式的拟合精度参数R2分别为 0.9902、0.9149、1。

也可以得喷射角度为45°时喷丸强度与喷丸压力间的关系：

该关系式的拟合精度参数R2为0.999。当喷丸强度的许用范围为0.15～0.25mm（A）时，可以计算得到喷丸压力的许用范围为0.13～0.27MPa。

2 喷丸参数优化

根据拟合所得的喷丸应力场参数与喷丸压力之间的关系，可以计算得到表1中不同参数下的喷丸应力值，将喷丸应力导入有限元模型模拟缘条的喷丸变形。以缘条变形后z方向的最大位移H作为不同喷丸参数下的缘条变形响应值，考察该响应值与各喷丸参数间的关系。

通过响应面分析，得到了响应值H与不同区域的喷丸压力之间的关系：

如图6（a）所示为缘条变形量与腹板下表面喷丸参数间的关系，可以看出，随着腹板下表面喷丸压力的增大，缘条的变形量减小。图6（b）、（c）分别为缘条变形量与腹板上表面及立筋表面喷丸压力间的关系，随着这两个区域喷丸压力的增大，缘条的变形量增大。

图6 缘条变形量与不同部位喷丸参数间的关系Fig.6 Relationship between deformation of the wing flange and peening parameters of different parts

由不同区域中喷丸参数对缘条变形量的影响规律来看，缘条的中性层位于腹板的上下表面之间。处于中性层下侧的腹板下表面上的喷丸强度与缘条的弯曲变形量呈反比关系，而其他两个区域的喷丸强度与之呈正比关系。与腹板上表面到中性层的距离相比，立筋到中性层的距离较大，所以缘条的变形量对立筋表面喷丸参数的变化较为敏感。

图6中竖直虚线所限定的范围为喷丸压力的许用范围。通过响应面分析，并结合喷丸压力的许用范围，得到了一组能使缘条变形最小的喷丸参数，即P1=0.27MPa、P2=0.13MPa、P3=0.13MPa，相应的变形量H=0.60mm。

根据实际的工艺条件，选取所获得的最优参数临近的喷丸参数作为试验参数，分别为P1=0.25MPa、P2=0.15MPa、P3=0.15MPa，相应的变形量H=0.64mm。

3 模拟结果与试验结果比较

优化参数P1=0.25MPa、P2=0.15MPa、P3=0.15MPa下的模拟结果如图7所示，为下缘条在z方向的位移场，缘条整体向立筋方向弯曲变形。

沿零件长度方向的直边边缘和曲边边缘测量其在z方向的变形量。将模拟变形量与试验值进行比较，如图8所示，从图中可以看出，模拟获得的变形趋势与试验结果相符；模拟变形量稍大于试验值；零件曲边的模拟变形量与试验值相符性较好，说明通过喷丸变形模拟能够较好地预测零件的喷丸变形。利用优化的喷丸参数强化后的机翼缘条零件的成形精度满足设计精度要求。

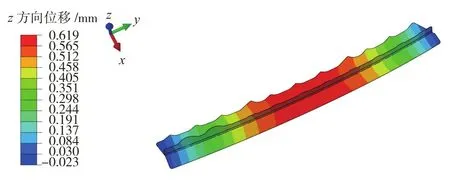
图7 有限元模拟的缘条在z方向的位移Fig.7 Displacement in the z direction of flange in finite element simulation

图8 零件z方向变形量试验测量与模拟对比Fig.8 Part deformation comparison of the experimental measurement and the simulation in the z direction

结论

通过喷丸强化应力的测量试验，建立了ASH230弹丸撞击2026-T3511铝合金材料产生的残余应力与喷丸压力等参数间的函数关系。

通过喷丸变形的等效有限元模拟，建立了机翼缘条的最大变形量与喷丸参数间的函数关系，得出了使机翼缘条喷丸强化变形量最小的喷丸强化参数，并通过缘条的喷丸强化试验验证了模拟的有效性。

[1]王欣， 江志华， 曾候祥， 等.喷丸对18%Ni型超高强度钢低周疲劳性能影响[J].北京航空航天大学学报， 2014，40(5)：608-612.

WANG Xin， JIANG Zhihua， ZENG Houxiang，et al.Effect of shot-peening on low-cycle fatigue property of 18% Ni ultra-high strength steel[J].Journal of Beijing University of Aeronautics and Astronautics， 2014，40(5)：608-612.

[2]LIU J， PANG M.Fatigue life prediction of shot-peened steel[J].International Journal of Fatigue， 2012，43：134-141.

[3]夏明莉， 刘道新， 杜东兴， 等.喷丸强化对 TC4 钛合金表面完整性及疲劳性能的影响[J].机械科学与技术， 2012，31(8)：1349-1353.

XIA Mingli， LIU Daoxin， DU Dongxing， et al.Effects of shot peening on surface integrity and fatigue properties of TC4 titanium alloy[J].Mechanical Science and Technology for Aerospace Engineering， 2012，31(8)：1349-1353.

[4]LI J K， MEI Y， DUO W， et al.Mechanical approach to the residual stress field induced by shot peening[J].Materials Science and Engineering A， 1991，147(2)：167-173.

[5]MIAO H Y， LAROSE S， PERRON C， et al.An analytical approach to relate shot peening parameters to Almen intensity[J].Surface and Coatings Technology， 2010，205(7)：2055-2066.

[6]杨德锴， 刘长安， 牛强， 等.金属板料抛喷丸仿真的有限元方法[J].机械科学与技术 ， 2010，29(6)：836-840.

YANG Dekai， LIU Chang’an， NIU Qiang， et al.Finite element method for shot blasting and shot peening simulation of metal sheet[J].Mechanical Science and Technology for Aerospace Engineering， 2010，29(6)：836-840.

[7]KIM T， LEE H， KIM M， et al.A 3D FE model for evaluation of peening residual stress under angled multi-shot impacts[J].Surface and Coatings Technology，2012，206(19)：3981-3988.

[8]徐虹， 滕宏春， 崔波， 等.残余应力非破坏性测量技术的发展现状简介[J].理化检验 ： 物理分册 ， 2003，39(11)：595-598.

XU Hong， TENG Hongchun， CUI Bo，et al.The state of the art and development on nondestruc-tive residual stress measurement[J].PTCA： Physical Testing， 2003，39(11)：595-598.

[9]陈会丽， 钟毅， 王华昆， 等.残余应力测试方法的研究进展[J].云南冶金，2005，34(3)：52-54.

CHEN Huili， ZHONG Yi， WANG Huakun，et al.Research progress of the method for residual stress measurement[J].Yunnan Metallurgy，2005，34(3)：52-54.

[10]LEVERS A， PRIOR A.Finite element analysis of shot peening[J].Journal of Materials Processing Technology， 1998，80：304-308.

[11]WANG T， PLATTS M J， LEVERS A.A process model for shot peen forming[J].Journal of Materials Processing Technology，2006，172(2)：159-162.

[12]GRASTY L V， ANDREW C.Shot peen forming sheet metal： finite element prediction of deformed shape[J].Proceedings of the Institution of Mechanical Engineers，Part B： Journal of Engineering Manufacture，1996，210(4)：361-366.

[13]GARIÉPY A， CYR J， LEVERS A， et al.Potential applications of peen forming finite element modelling[J].Advances in Engineering Software， 2012，52：60-71.

[14]GARIÉPY A， LAROSE S， PERRON C， et al.Shot peening and peen forming finite element modelling-towards a quantitative method[J].International Journal of Solids and Structures， 2011，48(20)：2859-2877.