基于水射流支撑的细长轴加工振动控制研究
(江苏信息职业技术学院,无锡 214153)
低刚度细长轴在人们的生活中和装备制造业中有着广泛的应用,但往往会因为其具有的特性影响其推广,如细长轴在加工过程中因切削力的作用而容易产生振动误差,该振动严重影响工件的加工质量,有时候还影响加工过程,使得加工中断。针对细长轴加工时产生振动的现象,国内外专家进行了相关研究[1]。Altinas[2]和Budak[3]等对工件切削加工过程中的稳定性进行研究,提出工件加工过程中振动稳定区域的预测模型,可以通过该模型求解出工件加工时的极限切削用量,有效地减小工件的振动。Weck[4]通过对机床的固有动态特性进行研究,可避免工件加工振动。Seguy等[5]分析细长轴在外载荷作用下的各阶模态和谐响应振动,建立细长轴在移动外载荷作用下的振动尺寸误差。Merdol等[6]和Thevenot等[7]分析不同的切削用量对细长轴振动的影响,建立其加工过程在外载荷作用下稳定性模型。Campa等[8]考虑刀具和细长轴之间相互耦合的作用,建立了三维动力学的切削稳定性模型,从而实现细长轴的精加工。
本文将水射流技术运用到细长轴切削加工,通过运用水射流辅助支撑细长轴来提高其刚度,从而减小细长轴在加工过程中的振动。
1 射流冲击模型
本文中的射流由喷嘴射到空气中属于非淹没流体,射流由喷嘴的入口端流入,出口端流出,如图1所示。假设流体在喷嘴中连续流动并不可压缩,应用粘性流体的伯努利方程可以将流体表示为[9-11]:

式中,p1、p2为流体流过喷嘴入口、出口流体产生的压力;v1、v2为流体流过喷嘴入口、出口的均速;ρ1、ρ2为流体流过喷嘴前、后的密度。
射流在喷嘴中流动可简化成流动参数只在某个方向有变化而其他方向的变化忽略不计的一元流动问题,并射流在喷嘴中连续流动,即可得下式:

式中,A1、A2为流体流过喷嘴入、出口截面的面积。
本文中喷嘴横截面为圆形,则喷嘴入、出口截面的面积A1、A2可以表示为

式中,d1、d2为喷嘴入口、出口直径。
联立式(1)~(4),可得喷嘴出口处流速:

本文喷嘴中的射流由喷嘴的结构可知,d1/d2≤1,p2≤p1,并水射流的密度ρ=998kg/m3,等式(5)可以简化为

由图1可知,喷嘴射出的流体流量q由喷嘴的出口截面积A2和流体在喷嘴出口处的流速v两因素共同决定,即:
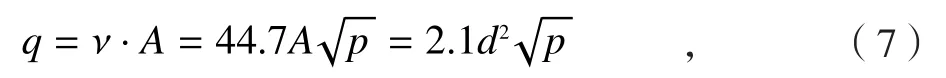
式中,q为射流流量,L/min;d为喷嘴出口直径,mm;p为喷嘴入口流体压力,MPa。
经喷嘴射流的流体撞击到细长轴产生的冲击力F由流体的流速v和单位时间冲击到工件上的流量q共同决定,即:

式中,Q为单位时间冲击到细长轴上的流量,m3/s;v为流体从喷嘴出口射出的速度,m/s;φ为射流冲击工件和离开工件的夹角。

图1 喷嘴结构示意图Fig.1 Schematic diagram of nozzle structure
2 细长轴振动动态特性分析
2.1 细长轴加工力学模型
细长轴切削加工过程主要外载荷为其受到的x、y、z方向的切削力,分别为轴向切削力Fx、背向力Fy、主切削力Fz。根据相关文献可知,上述各个方向的切削分力都会引起细长轴产生振动和变形等尺寸误差,而且背向力Fy对细长轴产生尺寸误差的影响远远大于轴向切削力Fx和主切削力Fz产生的尺寸误差。故本文仅分析和建立细长轴在xoy平面的受力模型。
本文中细长轴采用的装夹方式为顶针式。根据该装夹方可知细长轴的受力模型可以简化成工程上的超静定梁问题,简化后的受力模型如图2所示。卡盘对细长轴的约束可以简化为FAx、FAy和弯矩MA;车刀在xoy平面对细长轴产生的切削分力简化为F1x、Fy;射流对细长轴产生的冲击力简化为F2;顶针对细长轴的约束简化为支座约束反力FBy。

图2 射流辅助支撑车削力学模型Fig.2 Mechanical model of jet assisted support
细长轴加工过程背向力Fy是使其产生振动变形的主要原因。根据相关参考文献知,背向力的经验公式为:
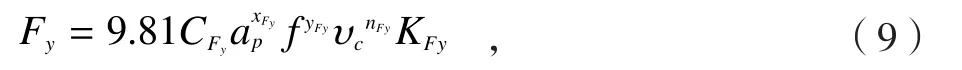
式中,ap、f、vc分别为切削背吃刀量、进给量、切削速度;CFy为工件材料对切削力影响相关系数;KFy为不同加工条件对切削力影响的相关系数;xFy、yFy、nFy分别表示公式(9)中背吃刀量、进给量、切削速度的指数。
2.2 细长轴径向振动分析
细长轴在切削加工时易发生径向振动,如图3所示,取细长轴上任意微小截面dx,在t时刻,此微小截面受振动而产生的位移为y(x,t),单位长度上受到的激振载荷为p(x,t)和外力矩为m(x,t)。
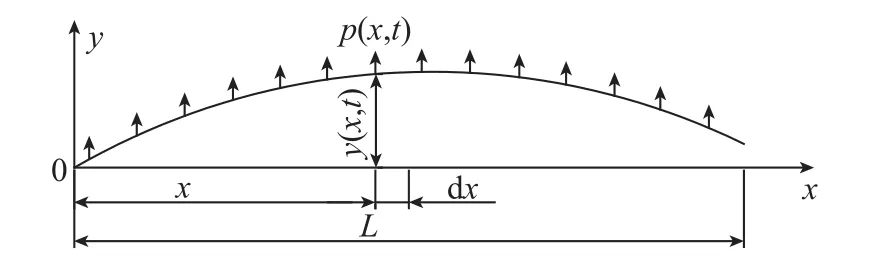
图3 细长轴径向振动示意图Fig.3 Schematic diagram of the radial vibration of slender shaft
由振动的微分单元法得到此微小截面在激振载荷p(x,t)作用下产生的振动微分方程为
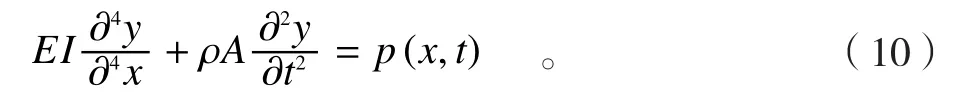
对于简化后的等截面细长轴,令p(x,t)=0,可得细长轴的径向自由振动方程为

式中:ρ为细长轴的密度;A为细长轴横截面积;E为细长轴的材料弹性模量;I为细长轴截面对中性轴的惯性矩。
由细长轴的径向振动基本理论,通过运用分离变量法,将式(11)用x的Y(x)与t(x)的谐函数的积分表示,其振动的固有频率可用w表示,即

将本文中的细长轴视为等截面梁,则式(12)的通解为

细长轴在切削加工过程中采用的装夹方式为一夹一顶,可得出细长轴加工时的主振型函数为

其中

2.3 细长轴切削力作用下的振动响应
细长轴在切削加工过程中受到的激振载荷p(x,t)=p(t)Y(x),其中p(t)为细长轴在切削时的径向受到的合力F,其大小为,其F的作用点位置x是个变量,,故可得

将等式(15)代入等式(10)可得

对y(x,t)进行坐标变换,并用qr(t)来表示更新后的坐标,即得

将(17)式分别对t求2阶偏导数、对x求4阶偏导数,运用正交性可得细长轴的振型为

由边界条件,细长轴在切削加工前,细长轴的挠度和速度都为0,则可求出上式的解

将等式(19)反带回等式(17),可得到细长轴在水射流辅助支撑的切削过程中切削点对切削力的响应,即为

因此,采用水射流辅助支撑细长轴切削加工可有效的降低其在加工过程中的振动,可使细长轴的表面精度提高。
3 试验
为了验证本文提出的以射流辅助支撑抑制细长轴振动的有效性,分别选两组细长轴分别进行有无射流辅助支撑加工的实验。细长轴的毛坯尺寸为 ,材料为45号钢。试验中采用的加工参数如下:背吃刀量ap=0.2mm,进给量f=0.1mm/min,切削速度Vc=60m/min;切削液射流发生系统中的参数如下:泵压为P=6.5MPa,喷嘴直径d=2mm,喷距L=1mm;采用的刀具是硬质合金车刀,刀具具体几何角度如表1所示。

表1 车刀的几何角度
本文首先任选一组细长轴进行普通车削加工,加工完成后采用JB-1C型粗糙度测量仪对其初始端及中间位置的表面进行粗糙度测量;再将细长轴按照本文提出的射流辅助支撑方法进行加工,车削加工完成后同样其在同一位置进行粗糙度测量,测得的结果分别由打印机打印出来。细长轴加工试验现场图如图4所示,粗糙度测量图如图5所示。

图4 细长轴加工试验现场图Fig.4 Experimental field of long axis machining experiment

图5 细长轴粗糙度测量Fig.5 Roughness measurement of slender long axis
从表面粗糙度的测试报告可知,无射流支撑时细长轴在初始端和中间位置的表面粗糙度分别为4.687 、5.917 ,有射流支撑时细长轴在初始端和中间位置的表面粗糙度分别为3.789 、4.058 ,由于细长轴初始段用三角卡盘进行装夹,故其比中间位置处的刚度大,振动小,表面粗糙度小。上述表明水射流辅助支撑可以提高细长轴的刚度,从而有效地控制其振动,使细长轴的粗糙度得到了较好的改善。
4 结论
本文针对低刚度细长轴在切削加工过程中因切削力作用而容易产生振动尺寸误差,将水射流技术应用到细长轴柔性辅助加工,以此提高细长轴的刚度抑制其振动尺寸误差,并通过研究了细长轴在水射流辅助支撑作用时的振动特性,获得细长轴辅助支撑时受切削力的响应方程,从理论上验证了水射流辅助支撑可很大减小细长轴的振动。最后,通过试验验证水射流辅助支撑技术可有效地提高细长轴的刚度和加工精度。
[1]杨叔子.机械加工工艺师手册[M].第2版.北京:机械工业出版社,2010.
YANG Shuzi.Handbook of machining process[M].Second Edition.Beijing: China Machine Process, 2010.
[2]ALTINTAS Y, BUDAK E.Analysis prediction of stability lobes in milling[J].Annals CIRP, 1995, 44(1):357-362.
[3]BUDAK E, ALTINTAS Y.Analytical prediction of chatter stability in milling-part I:general formulation[J].Journal of Dynamic Systems, Measurement, and Control, 1998, 120:22-30.
[4]WECK M.Handbook of Machine Tools[M].Wiley, 1984.
[5]SEGUY S, DESSEIN Q, ARNAUD L.Surface roughness variation of thin wall milling, related to modal interactions[J].International Journal of Machine Tools & Manufacture, 2008, 48(3-4): 261-274.
[6]MERDOL S D, ALTINTAS Y.Multi frequency solution of chatter stability for low immersion milling[J].Journal of Manufacturing Science and Engineering, 2004,126:459-466
[7]THEVENOT V, ARNAUD L, DESSEIN G.Integration of dynamic behavior variations in the stability lobes method: 3D lobes construction and application to thin-walled structure milling[J].International Journal of Advanced Manufacturing Technology, 2006, 27:638-644.
[8]CAMPA F J, LÓPEZ De Lacalle, LVIS N, Avoiding instability on the milling of parts with thin features[J].Materials Science Forum, 2006,526(3):37-42.
[9]刘军壮.高压水射流在再制造清洗中的应用[D].济南:山东大学,2012.
LIU Junzhuang.Application of high pressure water jet in cleaning of re manufacture[D].Jinan: Shandong University,2012.
[10]林府进,夏永军,周卫东.高压水射流冲击压力分布规律的研究 [J].矿业安全与环保,2008,35(1):8-10.
LIN Fujin,XIA Yongjun,ZHOU Weidong.Study on the distribution law of high pressure water jet impact pressure[J].Mining Safety and Environmental Protection,2008,35(1):8-10.
[11]张师帅.计算流体动力学及其应用-CFD软件的原理与应用[M].武汉: 华中科技大学出版社,2011.
ZHANG Shishuai.The principle and application of CFD software-CFD and its application[M].Wuhan: Huazhong University of Science and Technology Press, 2011.

