航空发动机叶片砂带抛光工艺参数优化

（西北工业大学现代设计与集成制造技术教育部重点实验室，西安 710072）

航空发动机依靠叶片完成对气体的压缩和膨胀，以最高效率产生强大的动力来推动飞机前进工作。叶片作为航空发动机的关键零件，具有材料难加工、曲面复杂、薄壁结构等显著特点，其质量的好坏对发动机的推进效率和使用性能有很大的影响，因此，制造出几何精度高和表面质量好的叶片，对于提升发动机性能和质量有着关键的决定性意义[1-2]。抛光作为叶片加工的最后一道工序，主要目的是保证其表面粗糙度和形状精度要求，使其具有良好的表面质量，达到最佳使用性能。

针对航空构件的抛光加工，Axinte等展开了砂带抛光Ti-6-4工艺技术及表面完整性的研究，分析确定了以砂带抛光作为发动机构件最终加工工艺的可行性[3-4]。在抛光过程中，工艺参数的选择对工件表面质量有很大影响，正确合理的选择抛光工艺参数对确保其表面完整性起着十分重要的作用[5]。Khellouki等对砂带磨抛的磨损机理及接触轮与工件之间的弹性接触进行了研究，并分析了工艺参数对工件表面粗糙度及材料去除率的影响[6]。Bigerelle等建立了砂带磨抛的磨损机理模型，并研究了工艺参数对表面粗糙度的影响[7-8]。重庆大学通过磨削试验分析了砂带的磨削机理，并对砂带磨削中不同工艺参数对工件材料去除率、工件表面形貌及表面质量的影响进行了研究[9-10]。

目前，国内外学者对加工工艺参数的优化进行了大量的研究。Alagumurthi等选取磨抛深度、砂轮线速度、进给速度为研究工艺参数，通过析因设计试验与田口试验两种方法对比，获取最优工艺参数及表面粗糙度[11]。Zain等建立了磨粒流加工中基于横移速度、射流压力、磨料粒径、磨料流量等工艺参数的工件表面粗糙度的二次回归预测模型，并分别用遗传算法、模拟退火法及两种方法的结合对工艺参数进行优化[12]。荆君涛等用响应面法建立磨具寿命与磨粒粒度、磨粒浓度、磨具内径的响应模型，对旋转超声磨削加工中的磨具寿命进行优化研究[13]。黄新春等研究了工件速度，磨削深度，砂轮速度对工件表面粗糙度的影响，并结合极差分析法获得了不同工艺参数对表面粗糙度的影响曲线，进行了磨削参数区间的优选[14]。上述研究大多针对平面零件，对于航空发动机叶片等复杂自由曲面类零件砂带抛光工艺参数优化的研究较少。

本文以砂带抛光航空发动机叶片工艺过程为研究对象，对抛光过程中的工艺参数进行优化。采用正交试验法进行叶片砂带抛光工艺试验，测量不同工艺参数组合下的叶片表面粗糙度。在此基础上，基于BP神经网络建立表面粗糙度与工艺参数之间的映射关系，建立表面粗糙度的预测模型。根据所建立的预测模型，以表面粗糙度最小为目标，分别采用遗传算法和粒子群算法对抛光工艺参数进行优化，获得最佳工艺参数组合。最后，通过试验对优化结果进行验证，为砂带抛光叶片工艺参数的选择提供基础数据。

1 试验方案

1.1 试验平台

试验装置为七轴五联动数控柔性抛光机床，如图1（a）所示。机床通过砂带机构实现对航空发动机叶片的抛光，如图1（b）所示，抛光过程中砂带机构可根据叶片型面的变化做出姿态的调整，工作轴为X轴、Y轴、Z轴3个直线轴与两个旋转轴U轴、C轴及摆动轴B轴，砂带机构转速范围为0～16000r/min。

1.2 试验目标和工艺参数的确定

在诸多的表面完整性特征中，表面粗糙度对零件疲劳性能的影响最为严重。因此，本文选用抛光后叶片的表面粗糙度作为试验目标。

叶片的砂带抛光试验中涉及了许多工艺参数，这些工艺参数的变化对抛光后叶片的表面粗糙度产生影响，然而，对每个工艺参数都进行优化十分困难也非常繁杂。根据前期的研究，本文选取对表面粗糙度影响较大的砂带粒度、接触力、砂带线速度、进给速度4个工艺参数为试验因素对其优化选择，其余对表面粗糙度影响不大的工艺参数在试验初定的参数范围内任意选取，本试验其余工艺参数固定为：接触轮硬度35A，磨抛深度6μm/次，磨抛次数4次，接触轮表面形式45°斜槽[15]。

1.3 抛光工艺试验

图1 数控柔性抛光机床Fig.1 CNC flexible polishing machine

以某型号航空发动机钛合金薄壁叶片为试验对象，选用布基、SiC磨料、合成树脂粘结剂砂带进行抛光，试验过程如图2所示。按标准正交表L27（313）安排试验，确定砂带粒度、接触力、砂带线速度、进给速度为4个试验因素，每个因素各选3个水平，如表1所示。抛光完成后，选用德国Mahr公司生产的MarSurf M300C表面粗糙度仪对叶片的表面粗糙度进行测量，每次测量选取叶片表面的3个不同测试点，取其粗糙度平均值作为试验结果。MarSurf M300C表面粗糙度仪如图3所示，试验方案与试验结果如表2所示。

图2 砂带抛光工艺试验Fig.2 Abrasive belt polishing process experiment

表1 砂带抛光因素水平表

图3 MarSurf M300C表面粗糙度仪Fig.3 MarSurf M300C surface roughometer

2 基于BP神经网络的抛光表面粗糙度预测模型的建立

2.1 BP神经网络结构设计

工艺参数的选择对抛光后叶片表面质量有重要影响，各因素间相互作用关系复杂，工艺参数与叶片表面粗糙度之间呈复杂的非线性关系，很难找到一个反应其内部规律的精确数学模型。人工神经网络具有自学习、自组织、自适应、并行处理信息能力和很强的非线性映射能力，尤其是误差反向传播网络（Back Propagation Network， BP网络）可以任意精度逼近任意连续函数，它只需要样本数据而不需要建立数学模型，就能建立起输入与输出之间的非线性映射关系。在不限制隐含层节点数的情况下，一个三层BP网络可以实现任意的n维输入层到m维输出层的映射[16]。因此，在本文中选择单隐层的BP神经网络建立预测模型。

根据砂带抛光叶片工艺参数对叶片表面粗糙度的影响，选取砂带粒度、接触力、砂带线速度、进给速度作为网络的输入参数，即网络的输入层节点数为4，其范围分别为 P100～P240，2～4N，7～15m/s，0.1～0.5m/min。网络的输出参数选取表面粗糙度Ra，即网络的输出层节点数为1。中间隐含层的节点数目在很大程度上影响着网络的预测性能，它与求解问题的要求、输入输出单元数多少都有直接的关系。如果隐含层节点数过少，则网络对复杂问题的学习能力不够，如果隐含层节点数过多，则会导致学习时间过长、误差不一定最佳，学习以后

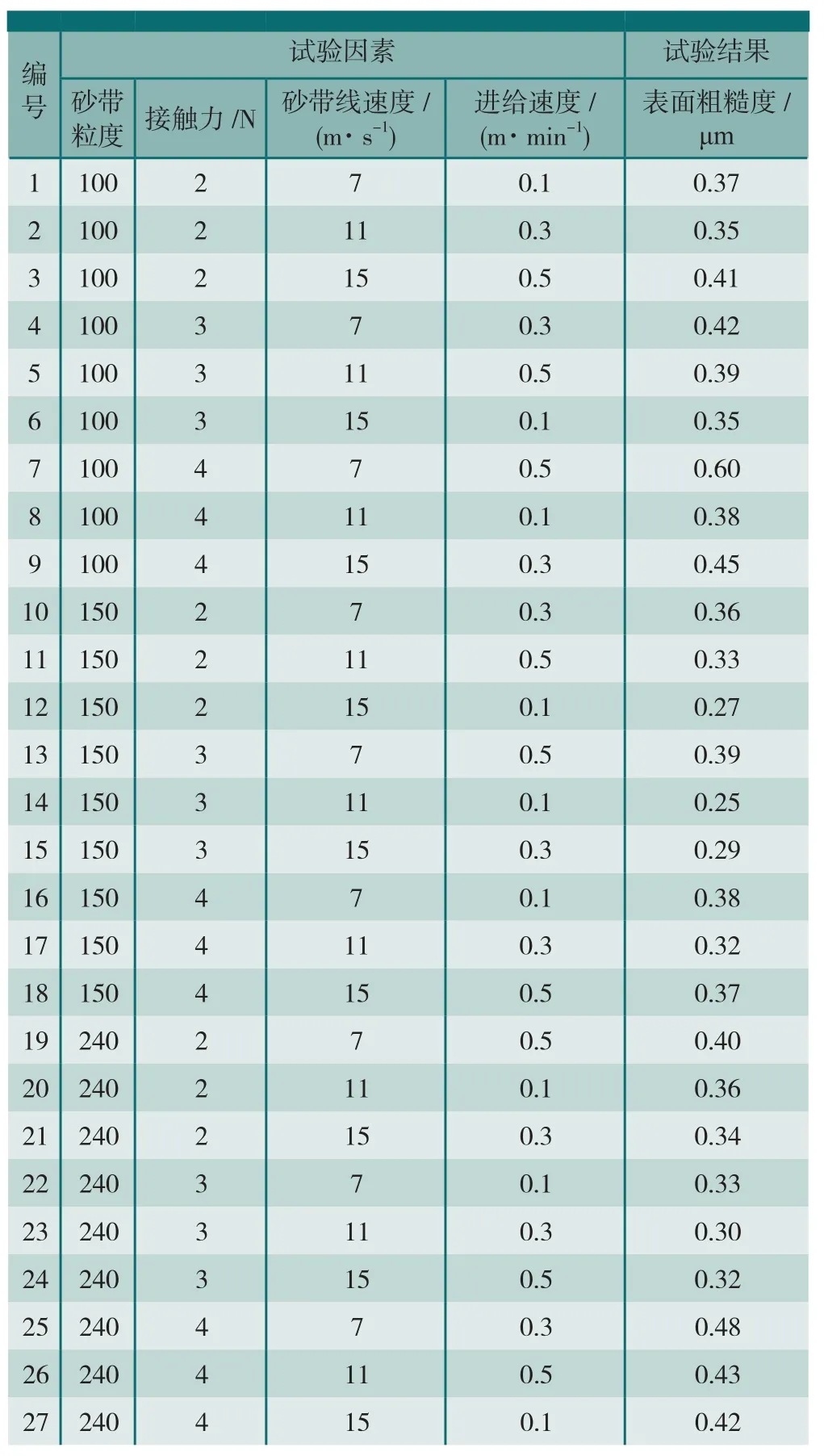
表2 砂带抛光试验方案与试验结果

网络的泛化能力变差。隐含层节点数目根据经验公式（1）确定[17]，即

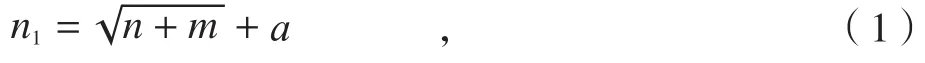
式中：n1为隐含层节点数，n为输入层节点数，m为输出层节点数，a为1～10之间的常数。由于输入层节点数为4，输出层节点数为1，则根据公式（1）隐含层节点数为4～13。但网络性能对节点数目比较敏感，因此比较实际的做法是用不同的隐含层节点数构建网络进行训练比较，综合网络的训练精度、映射速度以及训练误差，最终确定隐含层节点数为12。这样整个BP神经网络的结构为4×12×1的三层结构，如图4所示。

2.2 BP神经网络训练

根据图4所示BP神经网络结构构造输入输出模型，网络中间层的神经元传递函数采用S型正切函数tansig()，输出层神经元传递函数采用S型对数函数logsig()，网络的训练函数为trainlm()[18]。训练次数设置为500，训练目标设置为0.001，其他参数取默认值。选取表2中的27组试验数据作为BP神经网络的训练样本对网络进行训练，通过系统的自主学习及记忆能力不断修正网络的阈值和各节点之间的权值，当训练满足逼近精度或达到最大迭代次数时训练停止，网络训练好后用于预测非线性函数输出。

图4 BP神经网络结构Fig.4 Structure of BP neural network

2.3 BP神经网络测试

网络训练结束后，还必须利用另外一组试验数据对网络的性能进行测试，即利用仿真函数来获得网络的输出，然后检查输出和实际测量值之间的误差是否满足要求。测试样本数据及网络预测结果、误差如表3所示，表中Ra为表面粗糙度的实测值，Ra0为对应样本表面粗糙度的神经网络预测值， 为绝对误差， 为相对误差。图5为表面粗糙度样本值与BP神经网络预测值的对比，可以看出，样本值与网络训练的输出值十分接近。

从表3中可以看出，神经网络预测结果与试验结果误差较小，相对误差在3.52%以内，表明所建立的BP神经网络预测模型是准确可靠的，该模型可以有效的对砂带抛光叶片的表面粗糙度作出预测。误差产生的主要原因有：训练BP网络的样本数较少引起的预测精度偏低，测量误差造成的样本输入值与真实值之间的差异，以及网络拟合性能的局限性带来的偏差。

3 砂带抛光工艺参数优化

3.1 基于遗传算法的工艺参数优化

3.1.1 遗传算法

遗传算法（Genetic Algorithm， GA）是一种建立在自然选择原理和自然遗传机制上高度并行、随机和自适应的通用性优化算法，它通过模拟自然界中生物进化的发展规律实现特定目标的优化。遗传算法不依赖于函数求导，具有较强的适应能力，能有效地求解组合优化问题及其他复杂非线性问题，其编码技术和遗传操作比较简单，具有隐含并行性和全局解空间搜索等显著特点[19]。遗传算法通过对当前群体施加选择、交叉、变异等一系列遗传操作，从而产生新一代的群体，并逐步使群体进化最适应环境的状态，求得问题的最优解。遗传算法的优化流程如图6所示。

3.1.2 基于遗传算法的工艺参数优化

表面粗糙度的大小，对机械零件的使用性能有很大的影响，航空发动机叶片的加工对表面粗糙度有较高的要求，应使其值尽可能小，得到更光滑的表面。根据已经建立的表面粗糙度与砂带粒度、接触力、砂带线速度、进给速度之间的预测模型，运用遗传算法把训练后的BP神经网络预测结果作为个体适应度值，通过选择、交叉和变异操作寻找函数的全局最优解及对应输入值，即找到表面粗糙度的最小值及其对应的工艺参数。优化过程中，将表面粗糙度作为个体适应度，适应度值越小，个体越优。设定遗传算法的迭代次数为100，种群规模为20，交叉概率是0.4，变异概率是0.2，采用浮点数编码，个体长度为4[20]。优化过程中最优个体适应度值变化曲线如图7所示。

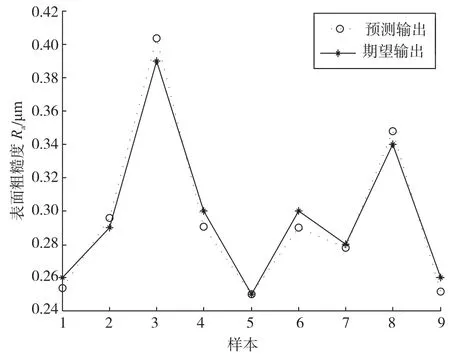
图5 BP神经网络预测结果与测试样本试验结果对比曲线Fig.5 Comparison between network output values and sample values

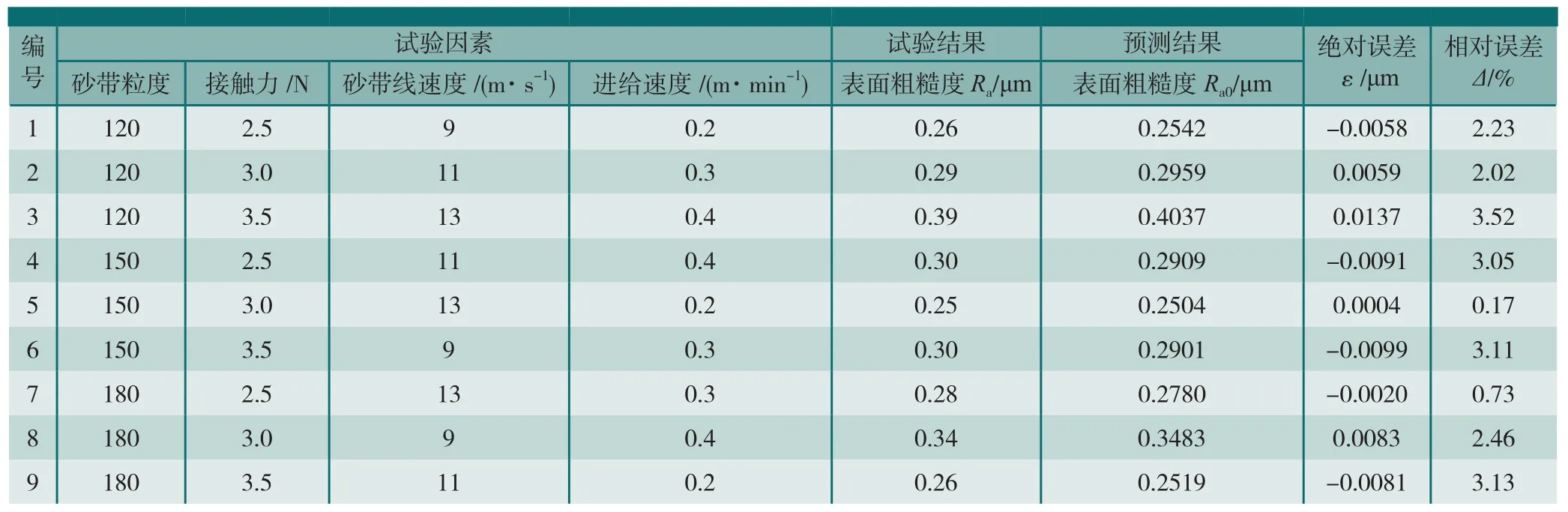
表3 测试样本的试验数据、试验结果及预测结果对比

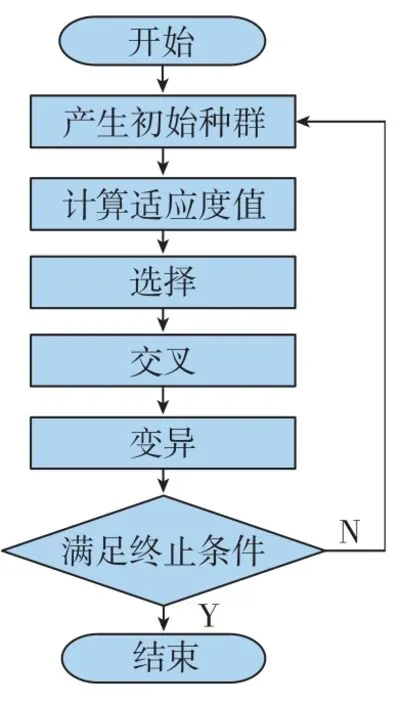
图6 遗传算法流程图Fig.6 Flow chart of genetic algorithm

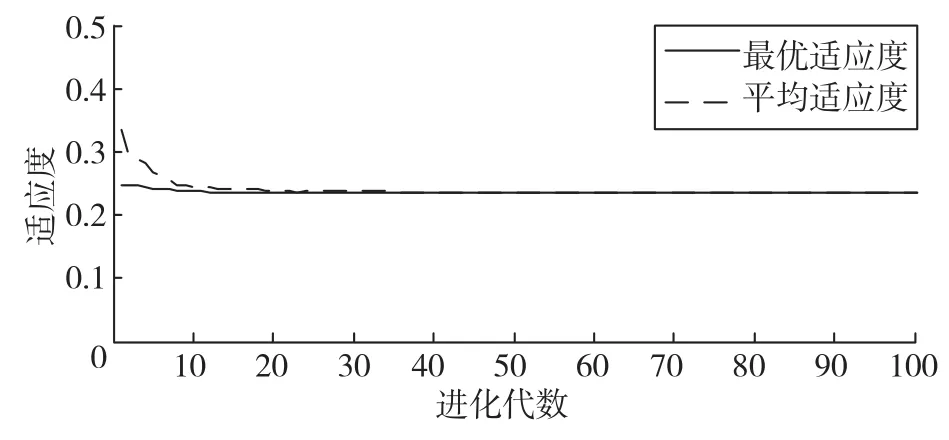
图7 遗传算法适应度变化曲线Fig.7 Genetic algorithm fitness curve

3.2 基于粒子群算法的工艺参数优化

3.2.1 粒子群算法

粒子群算法（Particle Swarm Optimization，PSO）是计算智能领域的一种群体智能优化算法，具有搜索速度快、效率高、算法简单、实现容易等优点，由Kennedy和Eberhart在1995年提出，该算法源于对鸟类捕食行为的模拟[21]。粒子群算法首先在可解空间中初始化一群粒子，然后通过迭代逐渐逼近最优解。粒子在解空间中运动，通过跟踪个体极值Pbest和群体极值Gbest更新个体位置。粒子每更新一次位置，就计算一次适应度值，并且通过比较新粒子的适应度值和个体极值、群体极值的适应度值更新个体极值Pbest和群体极值Gbest位置。粒子的速度决定了粒子移动的方向和距离，速度随自身及其他粒子的移动经验进行动态调整，从而实现个体在可解空间中的寻优。粒子群算法的优化流程如图8所示。

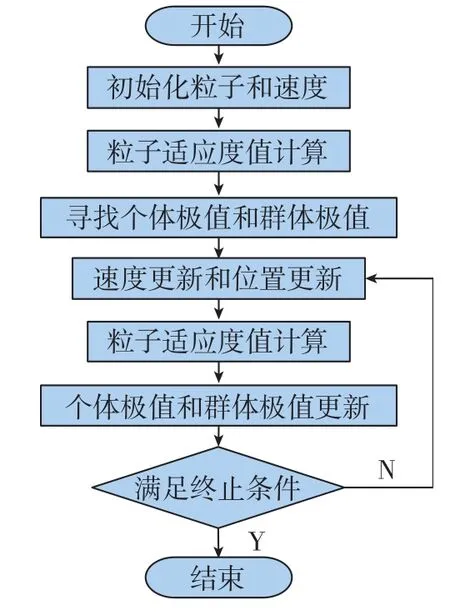
图8 粒子群算法流程图Fig.8 Flow chart of PSO

3.2.2 基于粒子群算法的工艺参数优化

基于建立好的表面粗糙度与砂带粒度、接触力、砂带线速度、进给速度之间的BP神经网络预测模型，将模型预测结果作为粒子的适应度值，适应度值越小，粒子越优，粒子群追随每次迭代中的最优粒子在解空间中进行搜索，进而实现砂带抛光工艺参数的优化。设定粒子群算法迭代进化次数为100，种群粒子数为20，每个粒子的维数为4，初始粒子位置和粒子速度取随机值[22]。最优个体适应度值变化如图9所示。

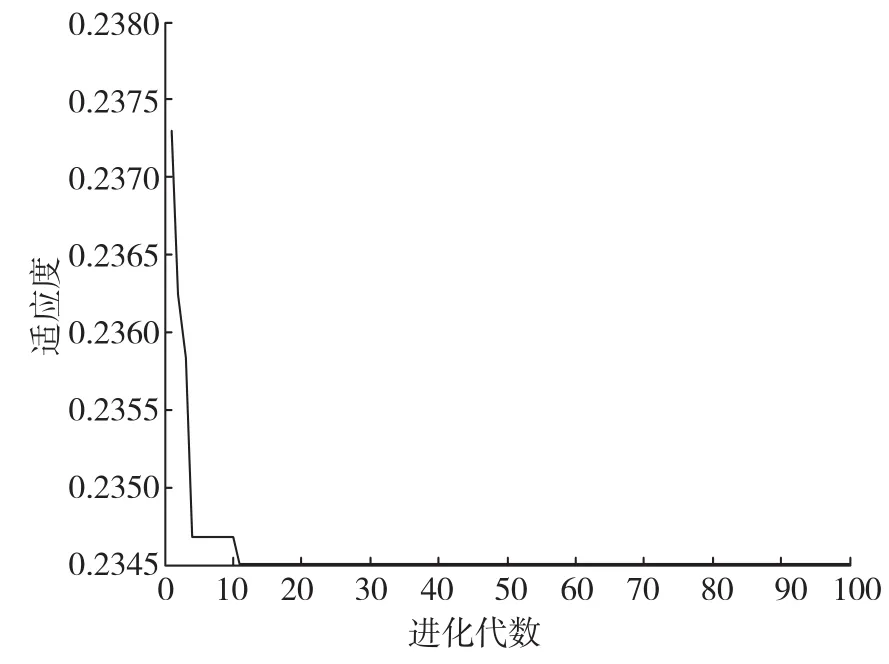
图9 粒子群算法最优个体适应度值Fig.9 PSO algorithm for best individual fitness value

3.3 优化结果

分别采用遗传算法和粒子群算法得到的优化结果如表4所示。由表4可以看出，遗传算法与粒子群算法得到的表面粗糙度最小值均为0.2345μm，砂带粒度、接触力、砂带线速度、进给速度4个工艺参数用两种方法得到的优化结果也十分接近。两种算法的相近结果表明优化结果是可靠的。由于标准砂带粒度只有P150，没有P152.5656和P151.8733，并对其他优化结果做四舍五入处理保留一位小数，得到最佳工艺参数：砂带粒度P150，接触力2.7N，砂带线速度8.5m/s，进给速度0.1m/min。

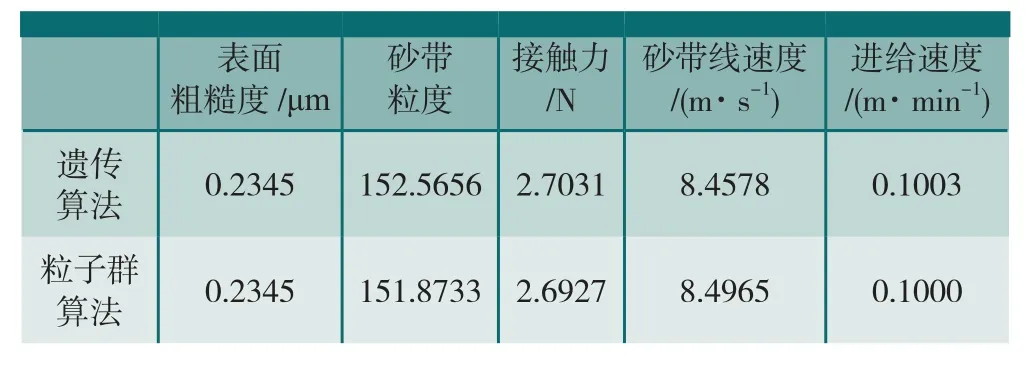
表4 遗传算法与粒子群算法优化结果对比

4 试验验证

采用优化后的工艺参数（砂带粒度P150，接触力2.7N，砂带线速度8.5m/s，进给速度0.1m/min）进行砂带抛光工艺试验，抛光前后叶片表面如图10（a）、（b）所示，检测抛光后的叶片表面粗糙度为0.22μm，小于优化前36组试验中的最小值0.25μm，优化效果显著。从图10可以看出，叶片表面铣削痕迹完全消除，光泽度有了较大提高，叶片表面质量得到了很大改善。

图10 优化后的工艺参数抛光前后叶片表面对比Fig.10 Comparison of blade surface between before and after polishing with optimized process parameters

5 结论

（1）利用BP神经网络建立了砂带抛光航空发动机叶片表面粗糙度与砂带粒度、接触力、砂带线速度、进给速度的神经网络预测模型，从而确定了叶片表面质量与抛光工艺参数之间的非线性关系。

（2）通过9组样本试验值与预测值的对比，相对误差在3.52%以内，表明所建立的BP神经网络预测模型是准确可靠的。

（3）基于所建立的BP神经网络预测模型，分别利用遗传算法和粒子群算法优化得到相近的结果，表明优化结果是可靠的。优化得到表面粗糙度最小时的最佳工艺参数为砂带粒度P150，接触力2.7N，砂带线速度8.5 m/s，进给速度0.1 m/min，经试验验证优化效果显著。

[1] 李小彪, 史耀耀, 段继豪 . 叶片数控砂带抛光关键技术研究[J]. 制造业自动化 , 2011,19：113-115,126.LI Xiaobiao, SHI Yaoyao, DUAN Jihao. Research on key technology for NC belt polishing of blade[J]. Manufacturing Automation, 2011,19：113-115,126.

[2] HUANG Y, YE X X, ZHANG M D, et al. Research on the key technology of NC abrasive belt grinding for the leading and trailing edges of aeroengine blades[J]. Advanced Materials Research, 2012, 565：76-81.

[3] AXINTE D A, KRITMANOROT M, AXINTE M, et al.Investigations on belt polishing of heat-resistant titanium alloys[J]. Journal of Materials Processing Technology, 2005, 166(3)：398-404.

[4] AXINTE D A, KWONG J, KONG M C. Workpiece surface integrity of Ti-6-4 heat-resistant alloy when employing different polishing methods[J]. Journal of Materials Processing Technology, 2009,209(4)：1843-1852.

[5] DAVIM, J. PAULO. Surface integrity in machining[M]. London：Springer, 2010.

[6] KHELLOUKI A, RECH J, ZAHOUANI H. The effect of abrasive grain's wear and contact conditions on surface texture in belt finishing[J].Wear, 2007, 263(1)： 81-87.

[7] BIGERELLE M, HAGEGE B, EL Mansori M. Mechanical modelling of micro-scale abrasion in superfinish belt grinding[J]. Tribology International, 2008, 41(11)：992-1001.

[8] BIGERELLE M, GAUTIER A, HAGEGE B, et al. Roughness characteristic length scales of belt finished surface[J]. Journal of Materials Processing Technology, 2009, 209(20)：6103-6116.

[9] 王维朗, 潘复生, 陈延君, 等. 不锈钢材料砂带磨削试验[J].重庆大学学报： 自然科学版, 2006, 29(10)：91-95.WANG Weilang, PAN Fusheng, CHEN Yanjun, et al. Investigation on abrasive belt grinding of stainless steel[J]. Journal of Chongqing University(Natural Science Edition), 2006, 29(10)：91-95.

[10] 朱凯旋, 陈延君, 黄云,等. 叶片型面砂带磨削技术的现状和发展趋势[J]. 航空制造技术, 2007,02：102-104.ZHU Kaixuan, CHEN Yanjun, HUANG Yun, et al. Present status and development trend of abrasive belt grinding technique for blade profile[J].Aeronautical Manufacturing Technology, 2007, 02：102-104.

[11] ALAGUMURTHI N, PALANIRADJA K, SOUNDARARAJAN V. Optimization of grinding process through design of experiment (DOE)—A comparative study[J]. Materials and Manufacturing Processes, 2006,21(1)：19-21

[12] ZAIN A M, HARON H, SHARIF S. Optimization of process parameters in the abrasive waterjet machining using integrated SA-GA[J].Applied Soft Computing, 2011, 11(8)：5350-5359.

[13] 荆君涛, 刘运凤, 李占杰, 等. 旋转超声磨削加工中影响磨具寿命的结构参数优化[J]. 光学精密工程, 2013,04：972-979.JING Juntao,LIU Yunfeng,LI Zhanjie,et al. Optimization of structure parameters affecting tool life in rotary ultrasonic grinding machining[J].Optics and Precision Engineering,2013,04：972-979.

[14] 黄新春,张定华,杨振朝,等. GH4169磨削表面粗糙度影响参数的敏感性研究[J]. 航空制造技术,2012,08：83-86,91.HUANG Xinchun,ZHANG Dinghua,YANG Zhenchao,et al.Study of Sensitivity of Parameter Affecting Surface Roughness in Grinding Superalloy GH4169[J]. Aeronautical Manufacturing Technology, 2012,08：83-86,91.

[15] 段继豪, 史耀耀, 张军锋, 等. 航空发动机叶片柔性抛光技术 [J]. 航空学报 , 2012, 33(3)：573-578.DUAN Jihao,SHI Yaoyao,ZHANG Junfeng,et al. Flexible polishing technology for blade of aviation engine[J]. Acta Aeronautica ET Astronautica Sinica, 2012, 33(3)：573-578.

[16] 蒋宗礼. 人工神经网络导论[M].北京：高等教育出版,2001.JIANG Zongli. Introduction to artificial neural networks. [M]. Beijing：Higher Education Press, 2001.

[17] 张立明. 人工神经网络的模型及其应用[M]. 上海：复旦大学出版社, 1993.ZHANG Liming. Model and application of aritificial neural networks[M]. Shanghai： Fudan University Press, 1993.

[18] 孙帆, 施学勤. 基于 MATLAB 的 BP 神经网络设计[J]. 计算机与数字工程, 2007, 35(8)：124-126.SUN Fan, SHI Xueqin. Design of BP networks based on MATLAB[J].Computer and Digital Engineering, 2007, 35(8)：124-126.

[19] 王小平,曹立明. 遗传算法——理论、应用与软件实现[M].西安： 西安交通大学出版社, 2002.WANG Xiaoping, CAO Liming. Genetic algorithm——theory application and software implementation[M]. Xi’an： XI’AN JIAOTONG University Press, 2002.

[20] 王东生, 杨斌, 田宗军, 等. 基于遗传神经网络的等离子喷涂纳米 ZrO2-7% Y2O3涂层工艺参数优化[J]. 焊接学报, 2013, 3： 002.WANG Dongsheng,YANG Bin,TIAN Zongjun,et al. Process parameters optimization of plasma-sprayed nano-structured ZrO2-7%Y2O3coating based on genetic neural network[J]. Transactions of the China Welding Institution, 2013, 3：002.

[21] KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of IEEE international conference on neural networks.Perth：IEEE, 1995,1942-1948.

[22] SRINIVAS J, GIRI R, YANG S H. Optimization of multi-pass turning using particle swarm intelligence[J]. The International Journal of Advanced Manufacturing Technology, 2009, 40(1-2)：56-66.