基于遗传算法的某汽车外形空气动力学优化

赖晨光，陈小雄，文凯平，陆茂桂

(重庆理工大学 车辆工程学院，重庆　400054)



基于遗传算法的某汽车外形空气动力学优化

赖晨光，陈小雄，文凯平，陆茂桂

(重庆理工大学 车辆工程学院，重庆400054)

摘要：汽车外形气动优化设计属于多目标优化设计的领域。多目标优化的根本是寻找约束条件下的最优解集即Pareto解集。首先建立某轿车的简化模型并参数化汽车的前部翘角(angle 1)、前风窗角(angle 2)、后风窗角(angle 3)和尾部上翘角(angle 4)，通过拉丁超立方取样得出一组样本点，再利用FLUENT软件对该组样本进行模拟计算，得出气动阻力和升力。用遗传算法对该组结果进行数据迭代，找出Pareto解集，由此得出该款汽车具有最佳气动性能时的角度组合。

关键词：气动优化;参数化;数值模拟;遗传算法

目前，在空气动力学研究方面，国内外通常采用数值模拟与风洞试验验证相结合的方法。数值模拟计算速度快、适用范围广，且不受边界条件的影响，已广泛应用于汽车空气动力学的研究中[ 1-2 ]。随着汽车性能和行驶条件的不断改善，人们越来越注重汽车在高速下的空气动力特性。空气动力特性良好的汽车，可以使气流平滑地流过车身表面。一般气动阻力的85%来自压差阻力，其余15%为摩擦阻力。压差阻力中9%来自车身前端，而91%来自车身尾部(其值随车身长短及外形不同而定)[3]。汽车在高速行驶时为抵消气动阻力而消耗的发动机功率随车速增加而急剧增加，所以良好的气动造型有利于降低汽车燃油消耗，也有利于提升汽车动力性以及高速行驶时的操控稳定性。

1参数模型

参照某款轿车的外形数据建立模型。表1列出了该轿车的主要外形参数。对其进行几何简化建模，忽略后视镜、门把手等车身附件，并对车身做平整处理，最后得到的三维模型如图1所示。需要参数化的4个角度(如图2所示)的变化范围如表1所示。

表1　某轿车主要外形参数　mm

图1　某轿车的三维模型

(°)

图2　需要参数化的角度

2网格生成与CFD计算

2.1控制方程

流体的流动受到物理守恒定律的约束，即流动需要满足质量守恒、动量守恒和能量守恒3个方程[4]。通常情况下，非稳态的连续方程和N-S方程适用于湍流的瞬时运动。在笛卡尔坐标系下，速度矢量u在x,y,z方向的分量分别为u,v,w，表达式如下：

divu=0

其中：u为速度矢量；p为流体微元体上的压力；ρ为流体密度。

2.2湍流模型的选择

Realizablek-ε湍流模型中相对最新的两方程由 Shih 提出[5]，即新的湍流控制方程和针对于耗散率的传递方程，而这些是标准k-ε湍流模型和 RNGk-ε湍流模型不能实现的。所以在计算气动阻力时，采用Realizablek-ε模型效果最好。在计算升力时，数值模拟方法与试验方法的误差较大，当前尚无湍流模型能准确地模拟计算升力[6]。相比而言，用Realizablek-ε模型模拟计算升力效果较好。

2.3网格划分与边界条件的设定

本研究对象为某款轿车的简化模型。设定计算域中车头离模型入口4倍车长，车尾离模型出口10倍车长，计算域总宽为10倍车宽，计算域总高为8倍车高，如图3所示。采用非结构网格与棱柱网格结合的网格策略。湍流模型为Realizablek-ε湍流模型，速度入口为v=30 m/s，压力出口为pressure-outlet；为消除附面层的影响地面为移动壁面[7]。计算采用Quick二阶迎风格式，并由经验公式计算得到湍流耗散率为ε=0.028。

图3　计算域

3数据处理与遗传算法

3.1优化流程

利用拉丁超立方取样方法选取40个源样本点。该方法可任意选取样本，并且使输入的样本组合比较平均地布满全部的试验空间。所有的设计变量均只使用一次，所以该试验方法能以较少样本点表现出全部试验空间的特征，是一种效果好、平衡性好的试验取样方法。利用FLUENT计算源样本，用Kriging模型对结果进行初步拟合。

3.2遗传算法

遗传算法是模仿生物进化论中自然选择和遗传学机理的计算算法。遗传算法的起点是搜寻种群中可能潜在解的个体，而每个个体的内部某类基因排列组合又决定了个体表现，进而决定了整个种群是否是有代表关键问题的解集。在每一代中，凭借遗传算子的组合、交叉与变异选出对目标问题适应度好的个体构成新的种群，将会产生越来越适应环境的后代个体，即越来越能代表关键问题的解。最后末代的最优个体就可以作为目标问题的近似最优解。本文对源样本点采用遗传算法分析，即个体随机组成原始种群，经过对目标即整车的气动阻力和升力进行评估，选取优质个体作为父代，再对父代个体进行复制、杂交和变异繁衍子种群[8]。经过多次的迭代，种群适应性逐步增强，即最优个体逐步增多。在通常情况下，对于较大的种群与较多迭代次数，其优化质量也较高。另外，多目标优化不同于单一目标优化，因为多目标之间极可能是相互竞争关系，使得各个目标无法同时达到最优解[9]，即多目标最优解多数都是一个解集。正是因为遗传算法具有多目标优化的特点，该算法多用于航空航天与机器人智能控制领域，在汽车工业领域应用还较少。

4结果分析

气动优化的设计状态选定为轿车高速行驶(V=30 m/s),以整车阻力最小和升力适中作为优化目标。由于目标之间互相竞争并不能使阻力和升力同时达到最优，所以多目标优化最终是找到满足各目标权重系数的解，即Pareto最优解集。本文选择13个Pareto解进行再次模拟，计算结果如图4所示。

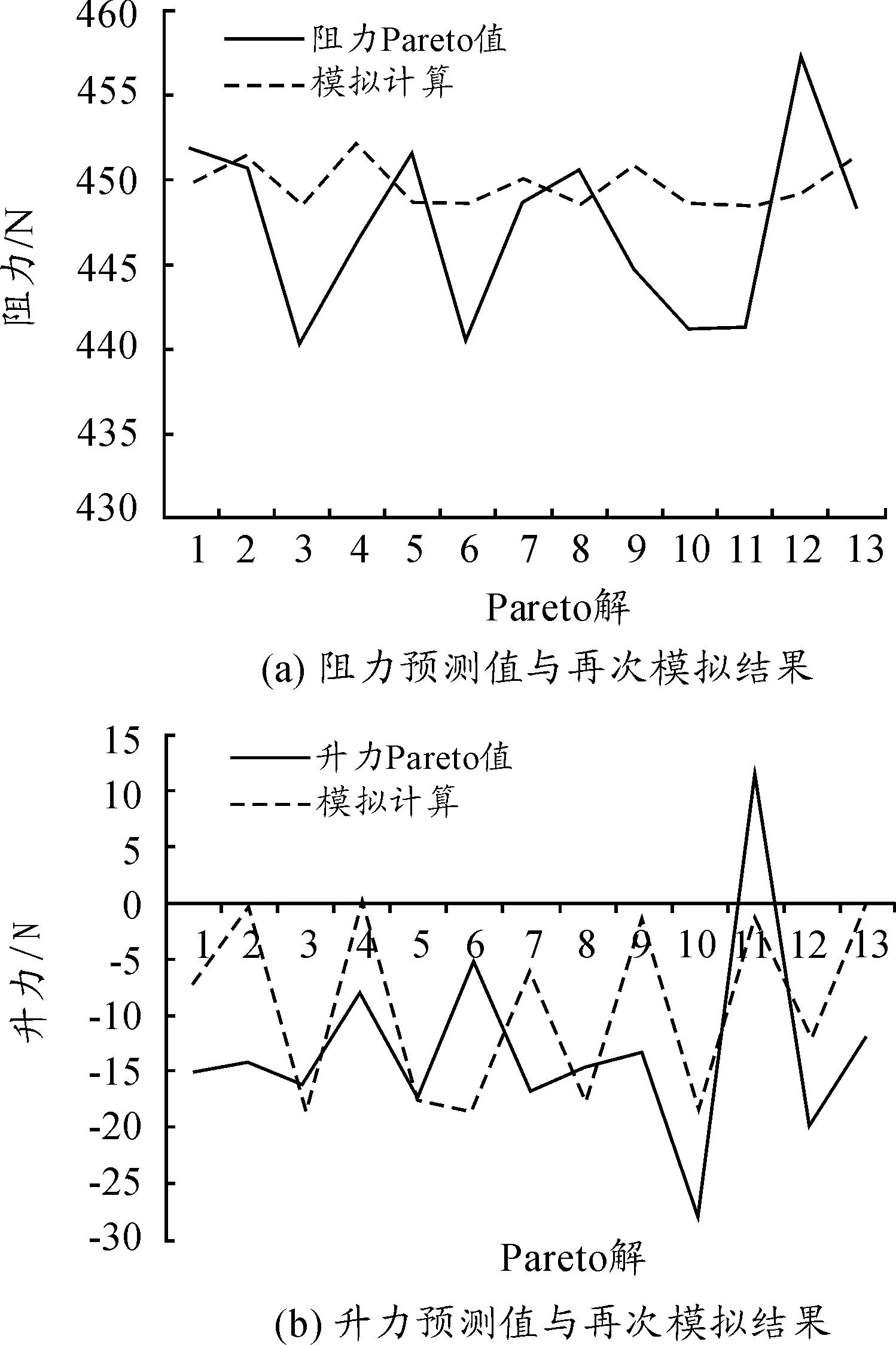
图4　预测值与再次模拟结果对比

由图4可以看出：同一样本点的阻力和升力偏差比较小，阻力偏差最大为8 N，升力偏差最大为14 N。预测结果与再次模拟结果比较接近，误差较小，结果比较准确。

通过相关分析得出各参数的全局敏感度，如图5所示。4个角度变量中angle 4尾部上翘角对升力影响最大，达62.5%；angle 2对升力影响最小，为3.4%。对于阻力4个角度变量影响都比较接近。

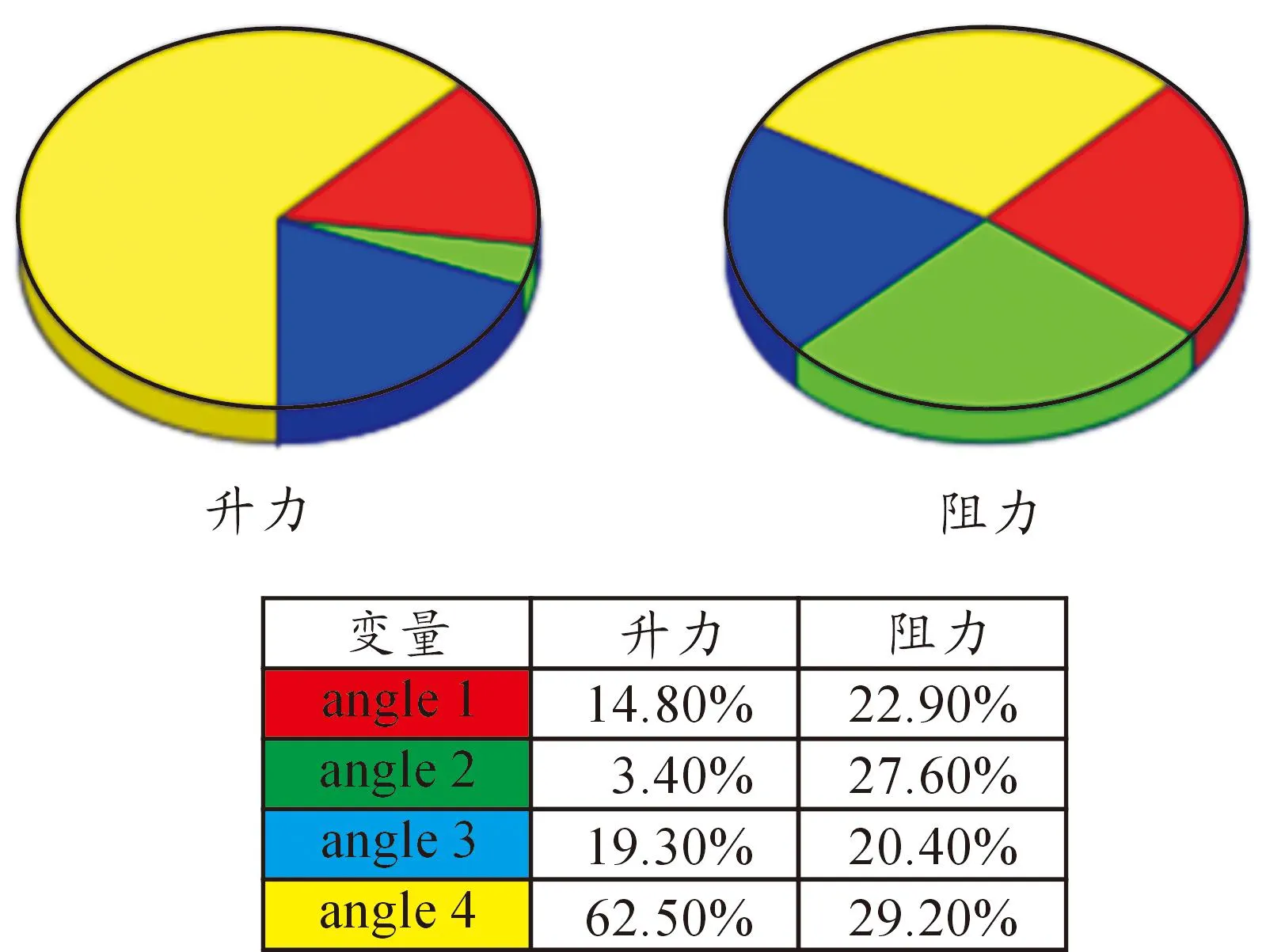
图5　敏感度分析

4.1模型计算结果对比分析

选取1个优化前的样本点(模型1)与优化后的样本点(模型2)进行模拟计算分析。模型1与模型2相关参数如表3所示。

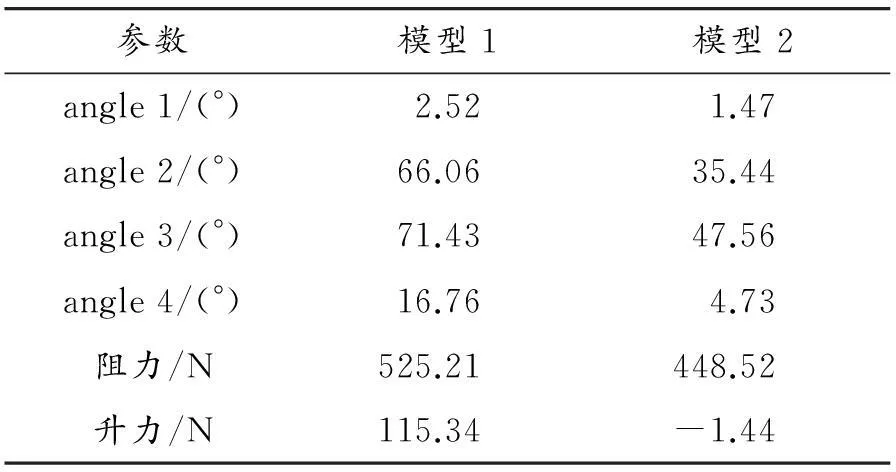
表3　优化前后两模型相关参数

由图6对称面压力云图可以看出：气流在流到汽车前端时受到车头阻碍，流动状态转变为相对静止，气流动压转变为静压，所以在两种模型的车头处都形成达到压力峰值的红色正压区，模型1红色正压区域稍大；两个模型在车头外缘处都形成负压区，模型2负压区域颜色较深，负压值较大；在车头上方发动机盖处可明显看到模型1气流分离区域颜色较深，分离剧烈，分离的气流再次附着流动并在空调进风口处形成橙色正压区域，模型1橙色区域明显较大；在两种模型的车顶前缘处都发生剧烈的气流分离，形成了明显的负压区域。汽车在行驶时会在尾部形成拖拽涡，由于尾部涡流能量损耗使得车尾压力下降，从而车头压力大于车尾，并因此产生了压差阻力。由图6可以看出：模型1车头前方正压区域大于模型2，车尾正压区域小于模型2，所以模型1的压差阻力大于模型2。因此，要降低汽车的压差阻力就要设法增大汽车尾部的压力并减小汽车前部压力。

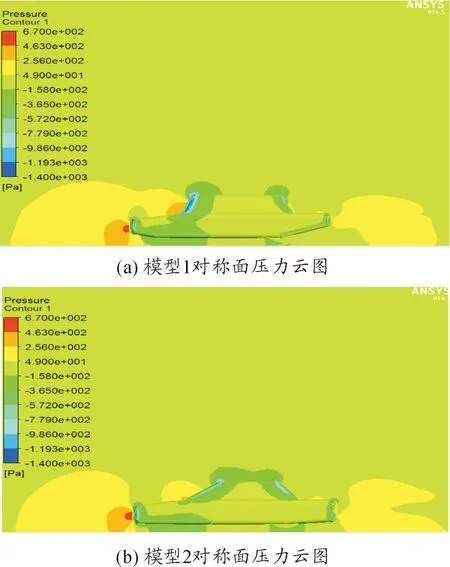
图6　对称面压力云图

由图7速度矢量图可以看出：两种汽车模型前部和尾部颜色为淡蓝色，说明气流速度非常小。在汽车尾部汇集的气流主要来自两部分：一部分流经发动机前盖、前风窗与车顶，然后流到车尾；另外一部分则直接流经车底盘与地面的间隙，再流到车尾。在模型2前风玻璃转折处相比模型1气流速度明显增大，气流流过该区域更加顺畅。在前风玻璃与车顶处模型1相比模型2呈现明显红色，气流速度高，发生明显气流分离。模型1后风窗倾角过大不利于前方气流向后顺利流动，所以形成的滞留区比模型2大。模型1增大了前部翘角，前方进入底部间隙的气流增多，大量气流进入会造成汽车升力增加，并且尾部上翘角的增大使得车尾最大离地间隙增大，车尾底部的气流会顺着车尾上卷进一步增大汽车升力。

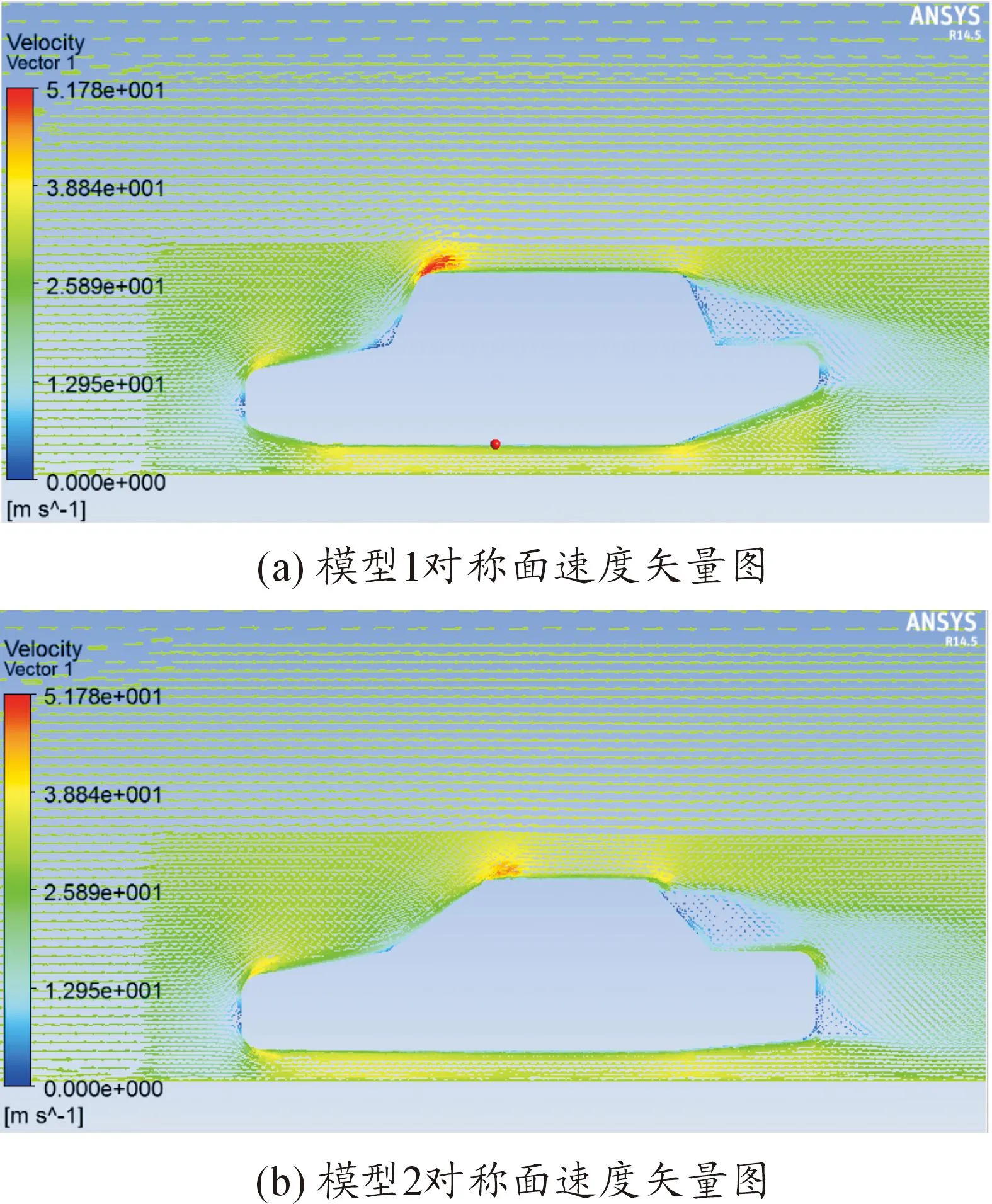
图7　对称面气流速度矢量图

模型1由于具有较大的尾部上翘角和较大后风窗角形成滞留区，使得汽车尾部没有明显的涡流,如图8(a)所示。模型2尾部有上下2个涡流，形成原理相同，都是因为尾部低压区导致来自汽车上部气流下卷或者汽车底部气流上卷，如图8(b)所示。可以明显看出：汽车尾部造型对气流的汇聚影响较大，即对整车气动阻力与升力均有较大影响。形成较大的涡流会损耗较多的能量，进一步降低汽车尾部压力，影响整车的气动阻力。所以，可以通过优化汽车车身外形等参数改善汽车流场特性，以此提高汽车的空气动力学特性。

图8　对称面尾部气流速度矢量图

5结束语

通过对比分析可见：优化后整车阻力减少了14%，升力变化较大，基本达到预期优化目标。

针对本文模型通过遗传算法预测出最佳角度组合的解集，并再次模拟验证，误差在5%以内，在可接受范围内，说明遗传算法可用于汽车外形优化。

通过以上分析可知：4个角度不是相互独立地影响汽车阻力和升力，相比之下尾部上翘角对整车阻力与升力影响最大。尾部上翘角会导致尾部气流上卷，不利于保持后风窗清洁，影响后风窗视野，进而影响汽车行驶安全性。

参考文献：

[1]王福军.计算流体动力学分析 [M].北京：清华大学出版社，2004：158-162.

[2]DODDEGOWDA P,BYCHKOVSKY A L,GEORGE A R.Use of computational fluid dynamics for the design of formula SAE race car aerodynamics[C]//SAE Pape.USA:[s.n.],2006.

[3]任斌.后扰流板对汽车空气动力学特性影响的模拟研究 [D].南京.：南京航空航天大学,2008.

[4]韩占忠，王敬，兰小平.Fluent流体工程仿真计算实例与应用 [M].北京：北京理工大学出版社，2005.

[5]SHIH T H,LIOU W W,SHABBI R A.A newk-εeddy viscositymodel for high Reynolds number turbulent flows[J].Comput Fliuds,1995,24(3):227-238.

[6]刘训，赖晨光.基于Ahmed模型的外流场数值模拟[J].重庆理工大学学报(自然科学)，2013,27(9):122-127.

[7]杜子学，陈振明.移动地面条件下的微型车外流场数值模拟研究[J].华东交通大学学报，2008(25):16-19.

[8]韩天时,赵旭,杨秋萍.厢式货车导流罩改进设计及气动优化[J].机械与电子,2010(10):19-22.

[9]韩天时,赵旭,杨秋萍.基于遗传算法的导流罩外形多目标气动优化设计[C]//2010中国汽车工程学会年会论文集.[S.l.]:SAE,2010.

(责任编辑刘舸)

Aerodynamic Optimization Based on Genetic Algorithm of Automobile Shape

LAI Chen-guang，CHEN Xiao-xiong，WEN Kai-ping，LU Mao-gui

(College of Vechical Engineering, Chongqing University of Technology, Chongqing 400054, China)

Abstract:Automotive exterior aerodynamic optimization design is a multi-objective optimization design field. The basic objective of solving multi-objective optimization problem is to get the best Pareto solution set. First, we established the simple model and got parameterization of front rake angle (angle 1), front windshield angle (angle 2), rear windshield angle (angle 3) and rear rake angle (angle 4). And we obtained sample points with Latin hypercube sampling, and then simulated the aerodynamic drag and lift of the samples by using FLUENT software. Using genetic algorithm data, we had iteration and found the optimum angle assembly for the best aerodynamic by finding the Pareto solution.

Key words:aerodynamic optimization; parameterization; numerical simulation; genetic algorithm

文章编号：1674-8425(2016)04-0001-05

中图分类号：U462

文献标识码：A

doi:10.3969/j.issn.1674-8425(z).2016.04.001

作者简介：赖晨光(1978— )，男，博士，教授，主要从事汽车与高速列车空气动力学研究；陈小雄(1988—)，男，硕士研究生，主要从事汽车外流场与汽车外形优化研究。

基金项目：国家自然科学基金资助项目(51305477)

收稿日期：2015-08-16

引用格式：赖晨光，陈小雄，文凯平，等.基于遗传算法的某汽车外形空气动力学优化[J].重庆理工大学学报(自然科学)，2016(4):1-5.

Citation format：LAI Chen-guang，CHEN Xiao-xiong，WEN Kai-ping，et al.Aerodynamic Optimization Based on Genetic Algorithm of Automobile Shape[J].Journal of Chongqing University of Technology(Natural Science)，2016(4):1-5.