新课改下中考数学“最短问题”的模型及应对策略

高尚军

摘 要： 针对课改下数学教学中存在的问题及对策，中考“最短问题”多以直线、角、三角形、特殊的平行四边形、梯形、圆、坐标轴、函数等载体出现.我们解题的对策是根据轴对称实现化“折”为“直”，利用“两点之间线段最短”、“垂线段最短”解决.

关键词： 新课改 最短问题 数学模型 应对策略

一、数学模型

1.两点之间线段最短

（1）如图1，直线l和l的异侧两点A、B，在直线l上求作一点P，使PA+PB最小.

（2）如图2，直线l和l的同侧两点A、B，在直线l上求作一点P，使PA+PB最小.（3）如图3，点P是∠MON内的一点，分别在OM，ON上作点A，B，使△PAB的周长最小.（4）如图4，点P，Q为∠MON内的两点，分别在OM，ON上作点A，B，使四边形PAQB的周长最小.

2.垂线段最短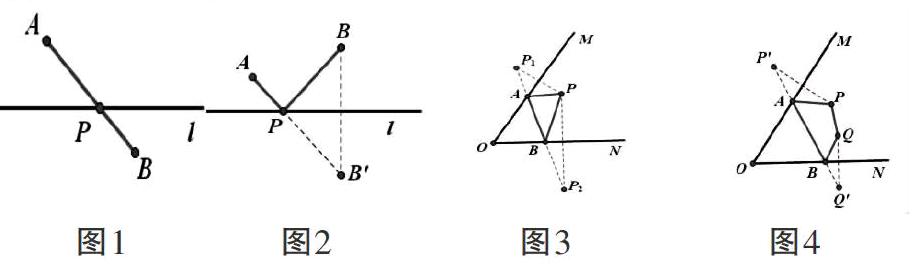

如图5，（1）点A是∠MON外的一点，在射线OM上作点P，使PA与点P到射线ON的距离之和最小.（2）点A是∠MON内的一点，在射线OM上作点P，使PA与点P到射线ON的距离之和最小.

二、应对策略

（一）利用“两点之间线段最短”解决

如图6，在矩形OABC中，已知A、C两点的坐标分别为A（4，0）、C（0，2），D为OA的中点，设点P是∠AOC平分线上的一个动点（不与点O重合）.

（1）试证明：无论点P运动到何处，PC总与PD相等.

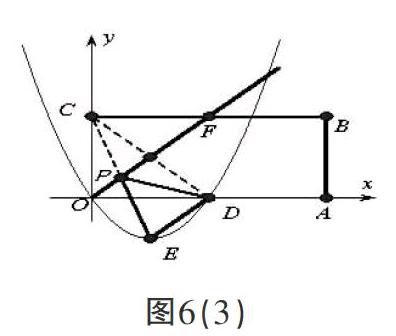
（2）当点P运动到与点B的距离最小时，试确定过O、P、D三点的抛物线的解析式. （3）设点E是（2）中所确定抛物线的顶点，当点P运动到何处时，△PDE的周长最小？求出此时点P的坐标和△PDE的周长.

（4）设点N是矩形OABC的对称中心是否存在点P，使∠CPN=90°？若存在，请直接写出点的坐标.

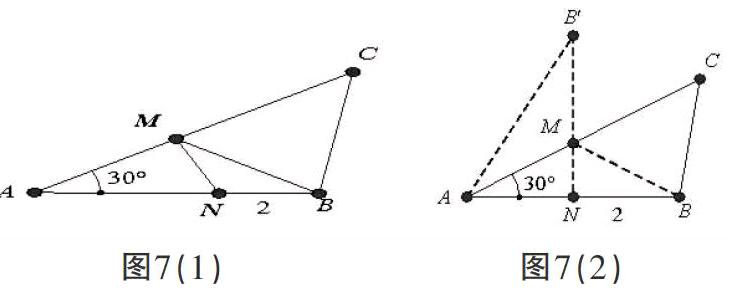
（二）利用“垂线段最短型”解决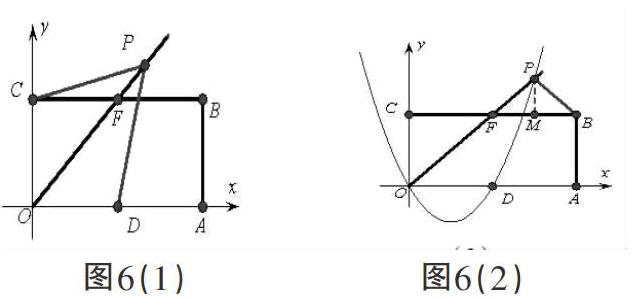

参考文献：

[1]中考试题汇编题解，2015.

项目名称：本文是2015年度甘肃省教育科学“十二五”规划课题《基础教育课程改革中的问题及对策研究》，课题批准号：GS[2015]GHB1546的阶段性研究成果之一。