“篮球落地”原始问题的实验与理论探究
张婷玉 胡扬洋 郑 旭
(1. 北京市陈经纶中学本部初中,北京 100020;2. 首都师范大学教育学院,北京 100048;3. 北京市第三十五中学,北京 100032)
·实验研究·
“篮球落地”原始问题的实验与理论探究
张婷玉1胡扬洋2郑旭3
(1. 北京市陈经纶中学本部初中,北京100020;2. 首都师范大学教育学院,北京100048;3. 北京市第三十五中学,北京100032)
摘要:针对全国物理高考命题委员会曾进行的高考物理科研试题测试中的“篮球落地”原始问题,笔者采用DIS系统进行了实验研究,并基于弹簧振子模型给出了理论解释,最后对研究结果与过程进行了讨论.
关键词:篮球落地;原始问题;物理模型;传感器
1“篮球落地”问题的提出
全国物理高考命题委员会曾在国内部分高中进行过高考物理科研试题测试,题目如下:
一篮球自某一高度自由下落,撞到地面后又弹起,升到一定高度后又自由下落,以后又弹起、下落,一次又一次,直至篮球静止.试定性画出在整个过程中篮球的加速度a随时间t的变化图线.
对该题,命题委员会给出的“正确答案”如图1所示.并且测试结果显示,本题的得分率相当低,只有6%.多数学生对碰撞过程中加速度的变化不清楚,也不会用图线表示加速度的变化.
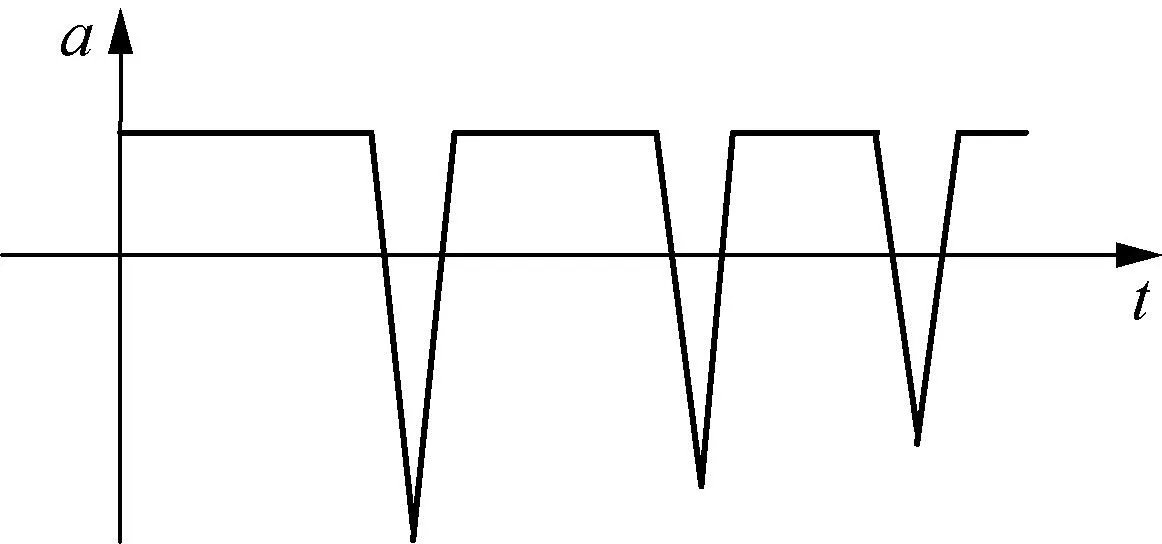
图1
我们认为,由于该题目没有提供任何数据,并且还需要对图像的诸多要素进行综合考虑,所以对学生的识图、绘图能力提出了较高要求,这或许是得分率不高的主要原因.然而在等“面积”法、斜率、形状等视角下很容易发现,命题委员会所给的“正确答案”依然存在诸多模糊之处.其根本原因是没有明确到底使用了什么模型,以及究竟经历了怎样的物理过程.为明确这一问题,我们进行了研究.
2实验设计与检验
首先,我们试图通过实验描绘出篮球落地实际情况的图线.由于篮球、网球等球类弹跳过程中的触地时间非常短,所以实验选用气球充入水模拟“篮球”.用力传感器及朗威DIS系统采集数据,得到“篮球”落地过程中,地表所受压力-时间图像如图2所示,易知,其与篮球的加速度-时间图像成几何相似关系.
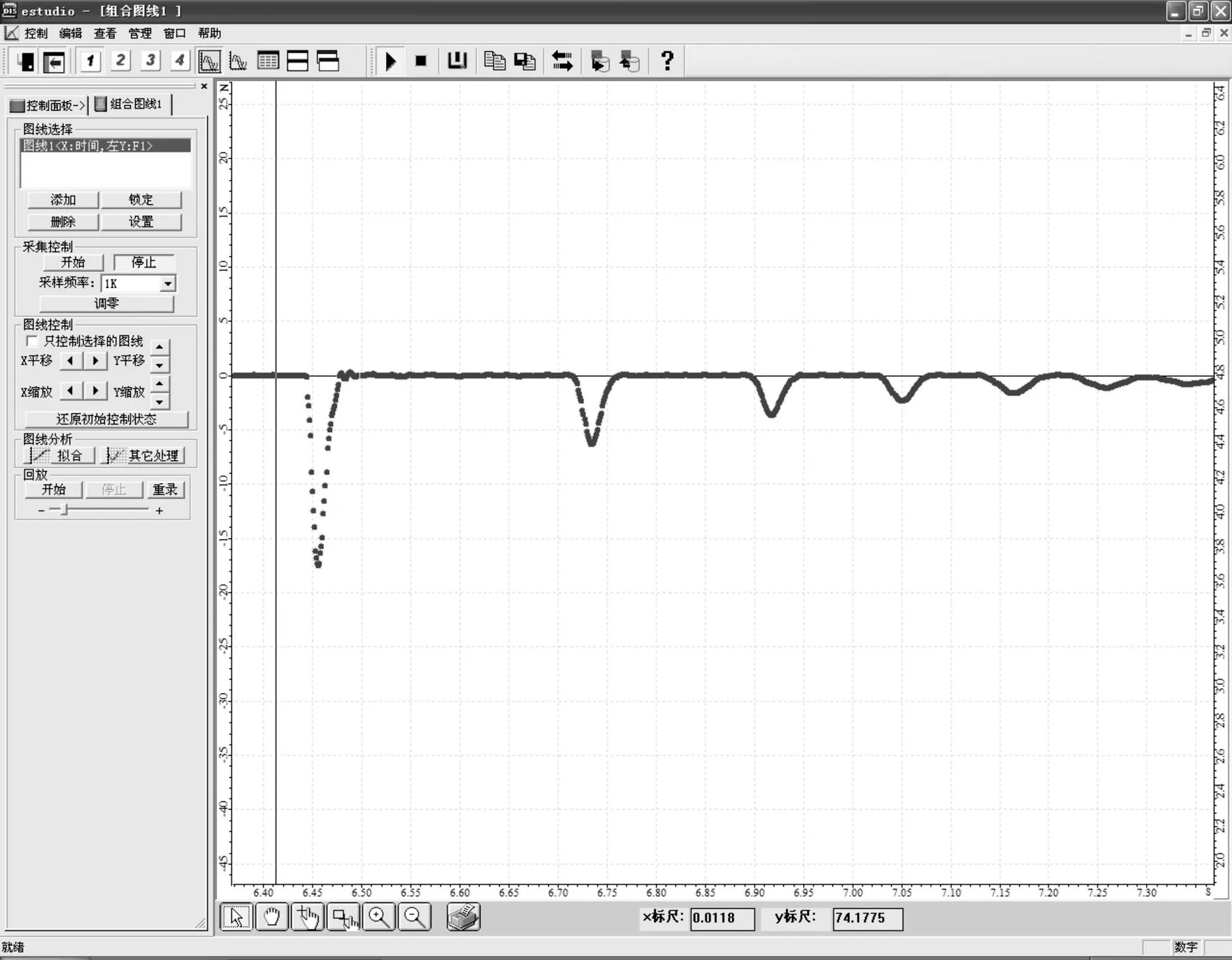
图2
如图2所示,图线在诸多细节上与“标准答案”的图线并不完全一致,整个过程的图像虽然左半部分与命题委员会给出的“正确答案”吻合较好,但是右半部分有更加细致的特点.此外,实验数据表明,“篮球”触地过程中的运动周期逐渐增大,这也同标准答案产生了明显的矛盾.据此我们需要基于以上实验结果得出篮球落地的数学表示.
3基于弹簧振子模型的理论解释
3.1精确解释
事实上,构建模型充分体现了物理学的学科特色,而该题的特殊之处在于需要分别建立恰当的实物模型和过程模型.综合考虑,我们将篮球视为一个特殊的弹簧振子模型(如图3所示),弹簧表征其弹性特征,振子表征其质量特征.

图3
在这一物理过程中,篮球之所以能逐渐静止,是因为其机械能在每次触地过程中存在损失.然而要想描出加速度-时间图像,仅有这样的功能解释是不够的,必须具体到动力学层面.为表征这一损失,我们首先做出一种假设:每次弹跳中劲度系数不变,压缩量发生“突减”.但是基于此做出的图像结果会造成图线在靠左的部分纵向无法收敛,因此舍弃了这一思路,选取了另一种假设:我们认为,弹簧振子在每次从最低点反弹的过程中,弹簧的劲度系数都会变小,这造成了弹簧“贮存”机械能的部分“失效”.依据这一模型的图像如图4所示.

图4
如图4所示,篮球由静止开始下落,加速度为g,从触地开始做简谐运动,直到压缩至最低点.在开始反弹时刻,由于劲度系数突然变小,导致反弹过程中简谐运动的变化主要有:(1) 加速度的最大值变小(即加速度幅度变小);(2) 周期变长;(3) 平衡位置降低,使得振幅变小,且多个周期后可能无法弹起而只能在弹簧原长以内运动.据此,反弹过程先做周期变长、振幅变小的简谐运动,弹离地面后加速度为g,直到最高点静止.至此,就完成了一个周期的运动.
图线与横轴围成的“面积”表示速度,运用“等面积”法可得:在一个周期内,“面积”s1=s2,s3=s4,且s2>s3.两周期间则有s4=s5.基于以上认识,图像才被足够精确地描绘出来,与原图像对比可见:(1) 虽然图线的“平台”部分不断缩短,但是最后就会完全“退化”为简谐运动的图像;(2) 图线“谷”的部分虽然也不断变“浅”,但是却在不断加宽,并且始终有在横轴以下的部分;(3) 图像的整体趋势是不断向横轴靠近.至于图像的“面积”、形状等要素则是在原图像中完全没有考虑的.
3.2近似解释
精确解释下的一大缺点在于图线在周期间的不连续性,这亦同实验图像不符.为弥补这一缺陷,我们在上述精确解释的基础上给出一种近似解释.
篮球与地面接触发生碰撞压缩过程中,在极短的时间内地面给予篮球很大的冲量,其a-t图像如同脉冲信号一般,则加速度在极短时间内达到峰值,即图像中相反方向有一尖端.图线与横轴围成的“面积”表示速度的变化量,篮球的初始时刻的速度为零,篮球与地面碰撞速度变化量为零,即两个运动过程a轴与t轴所围成的“面积”和为零.篮球与地面接触的极短时间内,近似为简谐运动,其图像为正弦曲线,因要达到与自由落体时间段内相同的速度变化量,正弦曲线十分尖锐,故可以近似将压缩与形变恢复过程a-t图像“曲线改直”,看作一条直线.
最后,在篮球与地面接触的极短时间内,其x-t、a-t图像均为正弦曲线.如图5所示是为两个正弦曲线,分别表示篮球以不同速度撞地时的加速度时间图像,显然,篮球与地面的碰撞过程中,初速度越快,振幅大,恢复形变所用时间越短,即篮球与地面碰撞时间逐渐增加.我们之前对篮球与地面接触的过程进行了“曲线改直”处理,a-t图像的正弦效应很难辨别出来.

图5
综合以上因素,得出篮球落地过程a-t图像,如图6所示:
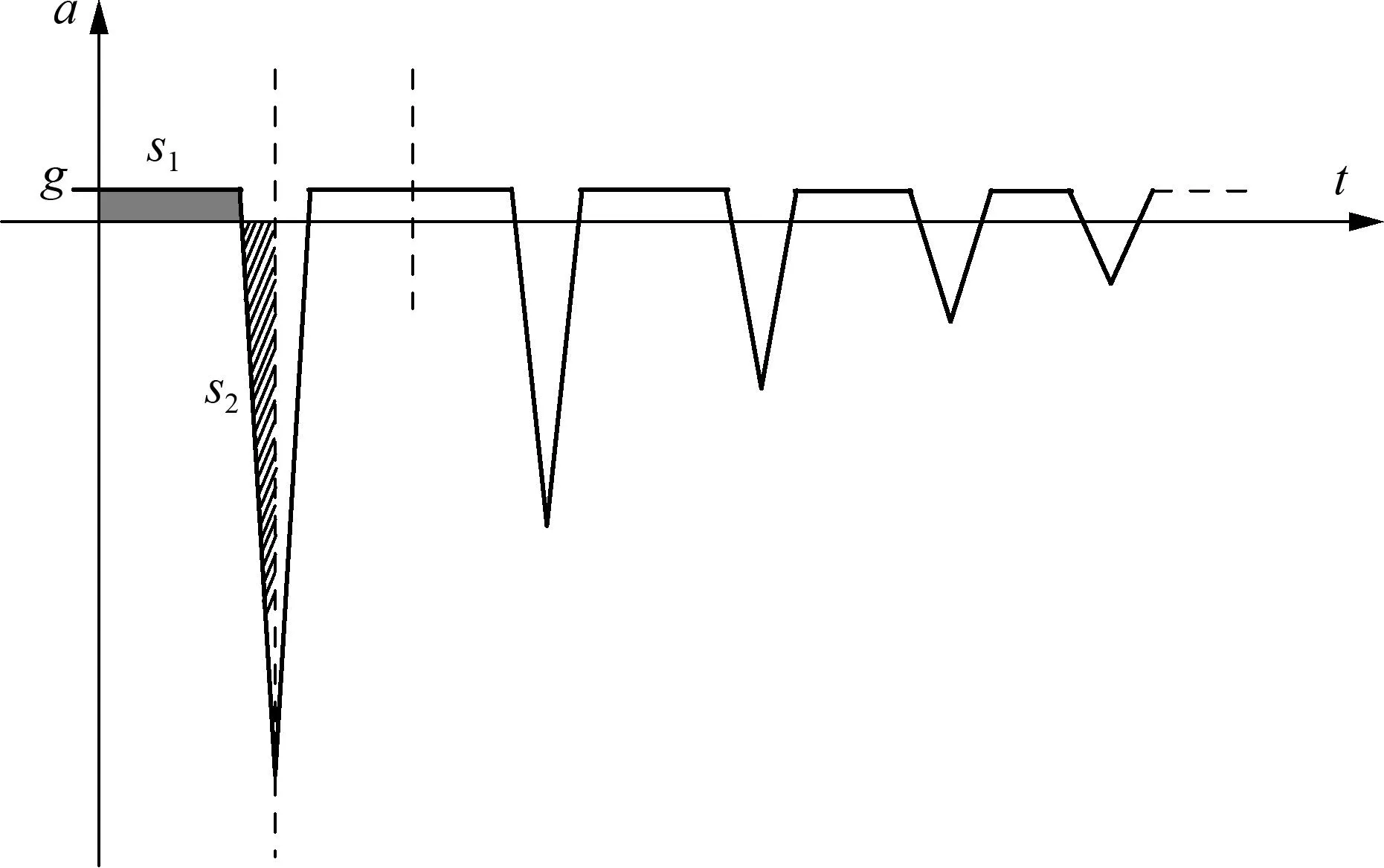
图6
如前所述,其中加速度与时间轴所围成的“面积”s1=s2.并且始终有在横轴以下的部分,图像的整体趋势是不断向横轴靠近.这一图像较好实现了精确与近似的统一,并体现了与原答案图像原则性的区别,因此可作为更好的“标准答案”.
4综合讨论
综合上述工作,我们对整个过程进行讨论.
4.1对研究结果的物理讨论
我们推导得出的图线中存在断点,这表明了理论模型本身的缺陷.但是值得肯定的是,以上对“篮球落地”的数学解释在整体趋势上与实验结果一致,尤其在图像左半部分成功地表征了实验图像更加精细的特点,但是在图像右半部分,误差被放大得更加显著.这不禁使我们想到了物理学史上的黑体辐射实验:对平衡时辐射能量密度按波长分布的曲线,维恩公式在短波部分与实验结果符合,而在长波部分显著不一致;瑞利-金斯曲线在长波部分符合,而在短波部分不符.最终普朗克给出了符合较好的黑体辐射公式,成为重要的研究突破.对篮球落地问题,如何提出在左右部分均匹配较好的数学表达式,就是进一步研究的目标.
4.2对研究过程的教学讨论
“篮球落地”问题不仅是一道一般意义上的“图像题”,而且被作为一道典型的原始物理问题,这体现了双重的教育价值.“篮球落地”问题的正确解决需要综合考虑图像的斜率、形状、“面积”等诸多要素,充分体现了图像题的综合性与深广度.具体而言,物体图像将需要符号推理获得的信息一览无余地呈现,大量缩减了推理过程,因此可以极大地提高对物理内涵的把握水平.因此,“篮球落地”图像教学不仅调动了学生思维的积极性,而且加强了思维方法的有效训练.其次教师进行“篮球落地”问题讲解时,要建立恰当的物理模型和过程模型,这不仅需要高度的抽象概括思维方法、严密推理的逻辑思维方法,还需要形象思维的方法才能充分驾驭.综上所述,“篮球落地”原始物理问题由于具有生态性,还需要直觉、灵感思维的参与,因此可以实现对思维方法更加积极、完备的训练,值得在教学时加以选用.
参考文献:
[1] 高考物理科命题委员会“八五”科研课题组.高考物理能力考察与题型设计[M].北京:高等教育出版社,1997:141.
[2] 邢红军.等面积法则的推广与应用——兼论科学方法教育[J].河南教育学院学报(自然科学版),1994,13(2):29-31,34.

