一种快速矩阵束相量提取方法的研究

杨 洋， 肖湘宁， 陈鹏伟， 房 钊

(新能源电力系统国家重点实验室， 华北电力大学， 北京 102206)

一种快速矩阵束相量提取方法的研究

杨 洋， 肖湘宁， 陈鹏伟， 房 钊

(新能源电力系统国家重点实验室， 华北电力大学， 北京 102206)

电力系统的监控、保护及模态识别通常依赖于相量参数的准确程度，因而快速准确地提取各类相量十分重要。本文基于矩阵束算法，利用前后两个耦合时段的输入信号采样阵构成一个方阵，该方阵的特征值不仅表示前后两个时刻工频、谐波及其他各类分量的复幅值之比，也表示着各分量的极值点信息。通过求解该方阵的特征根，在已知初始相量前提下，即可得到所需各分量的相量值。为减少求解计算量，本文利用方阵的Krylov子空间来构造相量的最小多项式，快速求解代表特定分量的特征值。理论分析和仿真结果表明，本文提出的快速矩阵束相量提取方法，与传统矩阵束法相比，计算量显著减小且实现方式简单，不受非目标分量及频率偏移的影响，在较短数据窗内仍具有较高精度。该方法适用于工频信息的提取，也适用于各次谐波信息。

相量； 矩阵束； Krylov子空间； 最小多项式

1 引言

电力系统工频以及其他各类谐波相量参数，在电力系统事件录波、状态估计、系统保护、系统控制及系统仿真等各个方面有着广泛的应用。

随着对相量或其中某个特征量测量的深入研究，国内外学者已提出了很多相量测量算法，如三点算法[1]、离散傅里叶变换(Discrete Fourier Transform，DFT)算法及其改进算法[2-5]、最小二乘法(Least Square，LS)曲线拟合、Prony算法、矩阵束法[6,7](Matrix Pencil，MP)、卡尔曼滤波算法[8,9]、基于泰勒展开模型的算法[10]、小波变换[11]、定频率相量提取算法[12]等。

三点算法原理简单，运算量小，但其测量精度低，易受谐波和噪声干扰。广泛运用的DFT算法由于未考虑到非整次谐波和衰减非周期分量的影响，会产生频谱泄露和栏栅效应，其改进算法虽然在一定程度上改善了性能，但都带来了迭代计算、数据窗限制等问题。LS算法是将输入的暂态电气量与一个预设的含有非周期分量及某些谐波分量的函数模型按最小平方误差原理进行拟合[13]，其虽然可以消除任意暂态分量，但提取精度依赖于预设信号模型的完整程度，而预设模型的复杂性也会增加计算时间。卡尔曼滤波算法与LS算法一样，需要预设模型，根据设定的状态数目进行卡尔曼滤波，滤除各次谐波与噪声。

Prony算法与矩阵束算法都是基于衰减指数和的信号模型，前者通过对特征多项式的求解来确定信号模型的极点信息[14]，后者能通过奇异值分解来确定模型阶数，并构造两个相关矩阵求解与极点信息等价的广义特征值[6,7]。但是，上述两个基于衰减指数和模型的方法，其计算精度依赖于较长的数据窗与较高的模型阶数，而且矩阵求逆、奇异值分解或其他矩阵运算过程都较为复杂，不可避免地增加了计算量。小波变换、基于泰勒展开、定频率相量提取算法等方法虽然在稳定性方面得到改善，并且有效地提高了计算结果的精度，但同时也不可避免地增加了计算量、依赖较长的数据窗、引入迭代或存在其他缺陷。

上述方法都无法将精度、响应时间和运算速度有效统一起来，即现有单一方法无法完全满足电力系统实际工况下相量提取的实时性与准确性要求。

本文在矩阵束算法的基础上，提出了一种适用于电力系统电磁暂态仿真的快速矩阵束相量提取(Fast Matrix Pencil，FMP)算法，利用采样时段耦合的两个输入信号采样阵构成一个方阵，从该方阵特征值中获得所需相量变化信息。为减少计算量，利用方阵的Krylov子空间来构造向量的最小多项式，实现对所需部分特征值的快速求解，同时得到极值点信息与相量变化信息，实现对工频与其他各类谐波的相量提取。

2 算法原理

2.1 矩阵束法

电力系统中大部分被观测信号都可以看作是一系列具有任意振幅、相位、频率和衰减因子的指数函数的和，即由衰减余弦分量和衰减直流分量组成：

(1)

式中，信号y(t)分别有q1个衰减余弦分量和q2个衰减直流分量；Ai、Aj为对应分量幅值；θi为对应分量相位；αi,αj为衰减因子；fi为对应分量频率。

令M=2q1+q2，则式(1)的离散时间函数形式为：

(2)

(3)

(4)

式中，Δt为采样间隔；zi表示信号模型的极点信息；pi表示留数信息。

由采样序列y(n)构造出2个(N-L)×L的Hankel矩阵Y1与Y2：

(5)

(6)

式中，L称为束参数，合理地选取可以在一定程度上消除数据所含噪声，通常取值范围在N/3～N/2之间，从而Y1与Y2可表示为：

Y1=Z1PZ2

(7)

Y2=Z1PZ0Z2

(8)

式中

Z0=diag[z1,z2,…,zM]

P=diag[p1,p2,…,pM]

定义矩阵束

(9)

容易证明，Y2-λY1的秩为M，而当λ=zi时，Z0-λI的第i行等于零，矩阵的秩降低为M-1，可以看出，信号的极点即为矩阵对{Y2,Y1}的广义特征值，故而对上述极点信息的求取转化为求解式(10)特征值的过程，其表达式为：

(10)

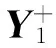
求得zi与M后，留数pi可利用最小二乘法的线性方程式(11)计算得到：

(11)

根据式(12)～式(15)，可求解出信号中包括基波分量在内的各类分量的幅值、相位、角频率以及衰减因子：

(12)

(13)

(14)

(15)

2.2 快速矩阵束法

本文所提出的快速矩阵束法是利用采样时段耦合的两个输入信号采样来构成一个方阵，并从该方阵特征值中获得所需相量变化信息，实现相量的快速提取。

对于y(kΔt)，分别从前一时刻t1和后一时刻t2开始截取数据窗长为N的序列，按式(16)与式(17)构成(N-L+1)×LHankel采样矩阵YE与YL：

(16)

(17)

式中，Δn表示两个测量起始时刻之间相差的采样次数，针对稳态与暂态情况可取不小于1的不同值。

式(16)与式(17)可写成：

YE=Z1PZ2

(18)

YL=Z1P′Z2

(19)

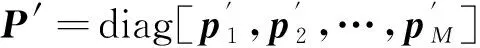
将YE的伪逆左乘YL，得到：

(20)

由式(20)可知：

(21)

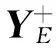
YL重新表示为：

YL=Z1PZΔnZ2

(22)

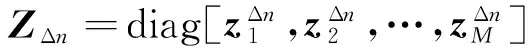
定义一个新的矩阵束如下：

(23)

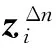
(24)

在相邻时刻，极值点变化量可忽略，即近似认为极值点信息相同。因此在初始稳定状态、已知初始相量的情况下，采用上述方法时，除在第一次求解时需要构造两个采样矩阵，后续相量提取可利用前一时段的采样阵。并且该方法无需求解模态数目M，即可以同时提取出较为准确的工频、各类谐波分量前后时刻相量变化信息。

2.3 特征值快速求取

对信号中某个或若干分量的提取工作并不需要完全求解所有特征值，本文通过构造向量的最小多项式来快速求解矩阵的目标特征值，以减小计算量，提高快速矩阵束方法的计算速度。

2.3.1 最小多项式的构造

已有相关定理证明[15]，对于任意矩阵A，存在非零m次的最小多项式fm(x)，使得fm(A)r0=0，且fm(x)=0的每个根一定都是矩阵的特征值，其中r0为A的某一列向量。因此矩阵A的部分特征值可通过求解fm(x)来获得。为求得向量r0的最小多项式，需找到最小的正整数m，满足r0,Ar0,…，Amr0线性相关，然后按照式(25)求解得到r0的最小多项式，如式(26)所示：

[r0,Ar0,…,Amr0](x0,x1,…,xm-1,1)T=0

(25)

f(z)=x0+x1z+…+xm-1zm-1+zm=0

(26)

由于构造的矩阵YE与YL须包含待观测信号所有的模态信息，矩阵阶数可能较大，会导致向量组r0,Ar0,…,Amr0的线性相关性开始变得模糊，并且Krylov矩阵[r0,Ar0,…,Amr0]不可避免变得病态，即不容易确定向量r0的最小多项式次数和精确求解线性方程组式(25)。

通过归一化Krylov[r0,Ar0,…,Amr0]矩阵的列，降低其病态程度，然后对其做QR分解，以R的秩作为r0的最小多项式次数，并求解：

(27)

从而得到r0的最小多项式：

(28)

2.3.2 最小多项式的求解

由于仅提取所需分量的对应特征值，且特征值所代表的极点信息变化范围一般较小，所以根据式(24)，给定较为合适的迭代初始值，迭代求解出目标特征值，从而可在较小的迭代次数下获得高精度的零点值。本文采用密勒法求解多项式零点。

3 仿真验证

本文在Matlab中实现快速矩阵束算法，通过给定信号评估各类谐波、衰减分量、不同数据窗长、频率偏移对工频及谐波相量提取精度的影响，并与离散傅里叶算法、最小二乘算法、Prony算法及传统矩阵束算法的提取结果进行比较。本文中，若无特殊说明，所有仿真的采样频率取10kHz，基波频率为50Hz，数据窗长取一个周波20ms，测量误差为0～40ms内连续测量的最大误差。

3.1 各种谐波和衰减分量的影响

为便于比较不同分量对快速矩阵束相量提取方法的影响，在不同给定信号中重复给定特定分量，构造的待测信号分别为：

(1)含整次谐波信号

10cos(3ω0t+π/4)

(2)含整次、非整次谐波信号

10cos(3.35ω0t+π/4)

(3)含整次、非整次谐波及衰减直流分量信号

10cos(3.35ω0t+π/4)+10e-t/0.1

(4)含整次、非整次谐波及衰减余弦分量信号

10cos(3.35ω0t+π/4)+

10e-t/0.1cos(4.45ω0t+π/3)

分别以上述信号中的基波相量，3.35次谐波相量为提取目标，连续滑窗测量40ms，采用本文的快速矩阵束法对信号x1(t)、x2(t)提取结果分别如图1和图2所示。

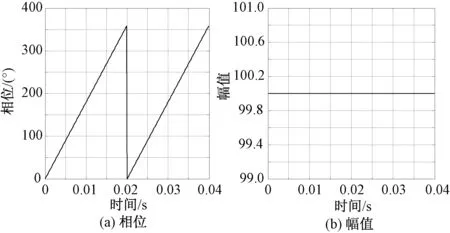
图1 含整次谐波信号滑窗测量工频相量结果Fig.1 Fundamental phasor extraction results containing integer harmonic components

图2 含非整次谐波信号滑窗测量3.35次谐波相量结果Fig.2 3.35 harmonic phasor extraction results of signal containing non-integer harmonic components

针对含直流衰减分量和余弦衰减分量的信号，分别以2次谐波与3.35次谐波分量为目标提取分量，滑窗测量幅值最大误差分别为3.01e-9%和6.53e-10%，图形与图1和图2类似，限于篇幅，不再重复列出。仿真结果表明，快速矩阵束相量提取结果不受非目标分量的影响。

分别采用离散傅里叶算法、最小二乘算法、Prony算法及传统矩阵束算法对上述4种信号进行测量，以基波分量为提取目标，其中离散傅里叶算法为全周傅里叶算法，最小二乘法的预设模型为不大于5次的工频、整次谐波与衰减分量的组合。提取结果如表1所示，其中Eamp表示幅值提取最大相对误差，Eang表示相位提取最大绝对误差。

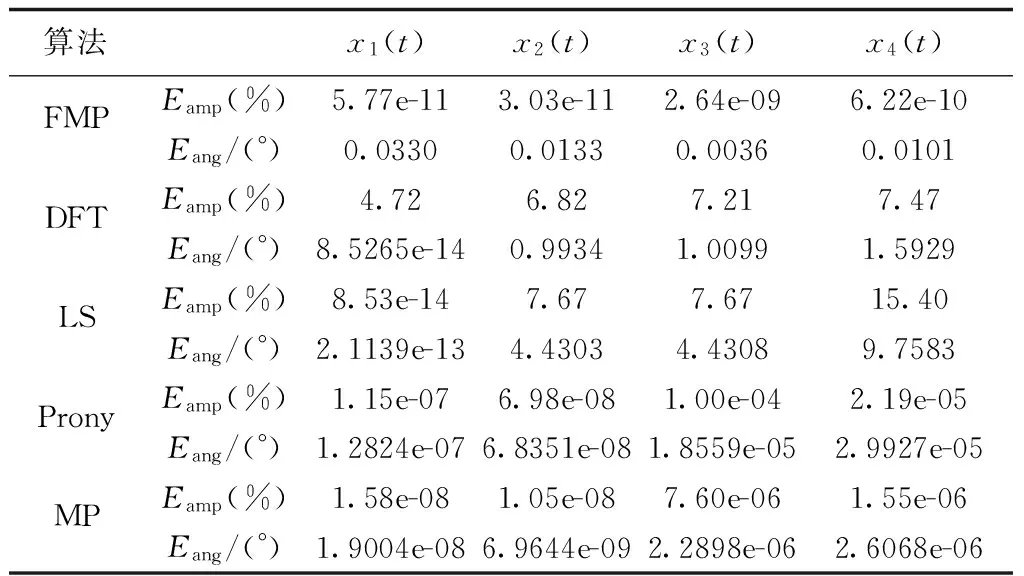
表1 不同信号类型下各算法的提取性能对比

表1的结果表明快速矩阵束方法由于累计误差的存在，在相角提取误差上稍大于传统矩阵束算法，但幅值提取仅通过极值点信息获得，因此结果更为精确。其总体精度远优于傅氏算法及最小二乘算法。

3.2 频率偏移的影响

当实际频率偏离额定值时，各分量相量的幅值、相角的测量误差都与初始相角有关。以0°为初始相角，分别采用DFT算法、最小二乘法、Prony算法及快速矩阵束算法对信号x3(t)连续滑窗测量，设定偏移频率为±0.5Hz与±1Hz，即取实际频率为49Hz、49.5Hz、50.5Hz、51Hz，以20ms数据窗连续测量40ms，采样频率设定为10kHz。幅值提取结果如图3所示。

图3 频率偏移下各算法幅值提取性能对比Fig.3 Comparison of amplitude extraction performance among various algorithms with frequency offset

图3的仿真结果表明，快速矩阵束算法同Prony算法一样，在幅值提取上几乎不受频率偏移的影响，且远优于DFT算法及最小二乘算法。

3.3 数据窗长的影响

对含不同分量的待测信号而言，其最小窗长限制也不同。针对信号x3(t)，改变窗长进行工频相量的滑窗测量，测量结果如表2所示，其中×表示幅值相对误差大于30%，相位绝对误差大于30°。

由表2可以看出，数据窗长为基波周期非整数倍时，测量结果依然精确；幅值测量误差随着数据窗长的增大而减小，算法抗噪性能逐渐增强；相角测量误差由于累计作用，存在一定波动性，但始终保持较为准确的提取精度。

4 结论

本文提出了一种适用于电力系统电磁暂态仿真的快速矩阵束相量提取方法，它具有如下特点。

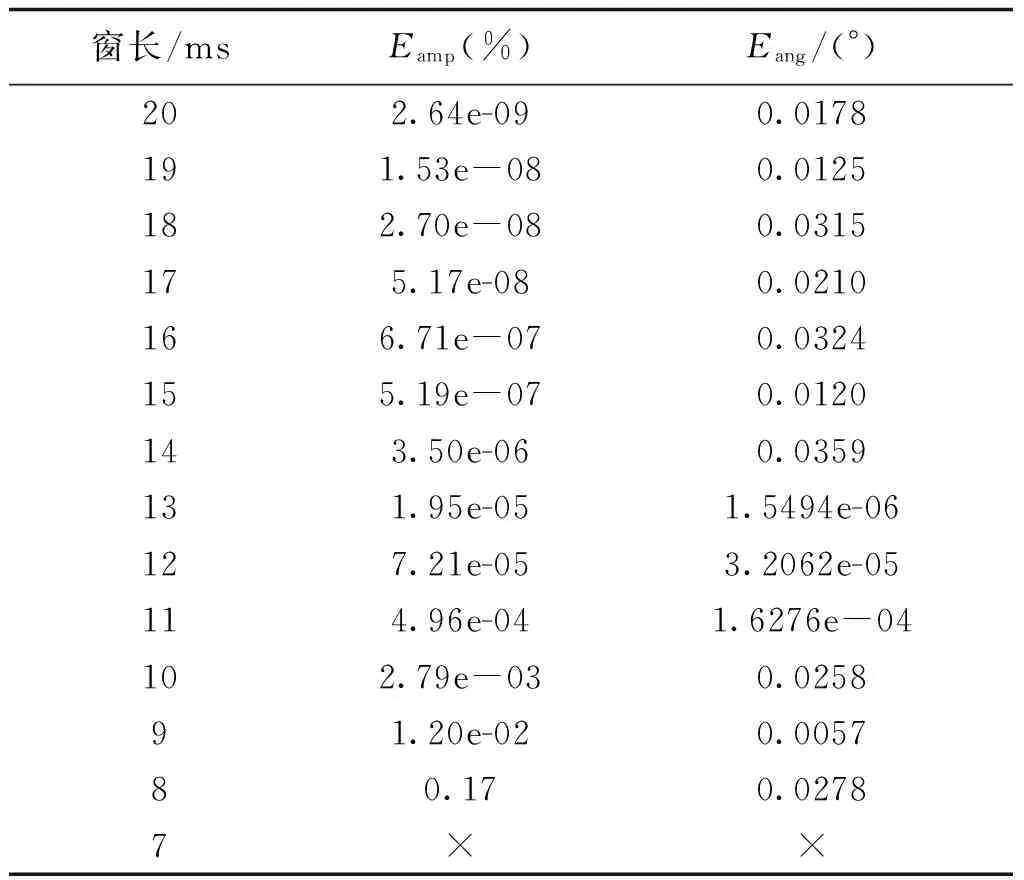
表2 不同数据窗长对快速矩阵束算法的影响

(1)与传统矩阵束算法相比，幅值提取仅涉及到矩阵求逆运算，因此提取结果更为准确。

(2)采用本文构造的向量最小多项式来求解部分特征值，实现简单，极大地减小了计算量。

(3)工频、各类谐波相量的提取结果不受非目标分量及频率偏移的影响。

(4)对数据窗长的限制小，提取结果在较短数据窗长内仍具有较高的精度，且数据窗越长，幅值提取结果越精确。

[ 1] 王晖，常鲜戎，郑焕坤(Wang Hui, Chang Xianrong, Zheng Huankun)．基于改进瞬时对称分量与三点算法的相量测量新算法(A method based on improved instantaneous symmetrical components and three-point algorithm for synchronized phasor measurement)[J]．电力系统保护与控制(Power System Protection and Control)，2011，39(19)：115-120．

[ 2] Yang J Z，Liu C W．A precise calculation of power system frequency and phasor[J]．IEEE Transactions on Power Delivery, 2000，15(2)：494-498．

[ 3] Maohai Wang，Yuanzhang Sun．A practical, precise method for frequency tracking and phasor estimation[J]．IEEE Transactions on Power Delivery，2004，19 (4)：1547-1552．

[ 4] T S Sidhu，Xudong Zhang，V Balamourougan．A new half-cycle phasor estimation algorithm[J]. IEEE Transactions on Power Delivery，2005，20(2)：1299-1305．

[ 5] David Hart，Damir Novosel，Yi Hu，et al．A new frequency tracking and phasor estimation algorithm for generator protection[J]．IEEE Transactions on Power Delivery，1997，12(3)：1064-1073．

[ 6] Sarkar T K, Pereira O. Using the matrix pencil method to estimate the parameters of a sum of complex exponentials[J]. IEEE Antennas and Propagation Magazine, 1995,37(1): 48-55.

[ 7] Hua Y, Sarkar T K. Matrix pencil method for estimating parameters of exponentially damped/undamped sinusoids in noise[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1990,38(5): 814-824.

[ 8] Kennedy K, Lightbody G，Yacamini R．Power system harmonic analysis using the Kalman filter[A]. IEEE Power Engineering Society General Meeting [C]. 2003. 2：757-761．

[ 9] Routray A，Pradhan A K，Rao K P．A novel Kalman filter for frequency estimation of distorted signals in power systems[J]．IEEE Transactions on Instrumentation and Measurement,2002，51(3)：469-479．

[10] 麦瑞坤,何正友，薄志谦(Mai Ruikun, He Zhengyou, Bo Zhiqian). 基于泰勒展开模型的同步相量估计新算法(A new transient method for earth fault line selection in resonant grounded power system based on morphological filtering)[J].电力系统自动化(Automation of Electric Power Systems), 2008,32(12):22-26.

[11] Wilkinson W A，Cox M D．Discrete wavelet analysis of power system transients[J]．IEEE Transaction on Power Systems，1996，11(4)：2038-2044．

[12] 索南加乐，王斌，王莉, 等(Suonan Jiale, Wang Bin, Wang Li, et al.)．快速相量提取算法(A fast phasor calculation algorithm for power systems)[J]．中国电机工程学报(Proceedings of the CSEE)，2013，33(1)：123-129．

[13] Sachdev M S，Giray MM．A least error square technique for determining power system frequency [J]．IEEE Transactions on Power Apparatus and Systems，1985，PAS-104(2)：437-444．

[14] 丁屹峰，程浩忠，吕干云, 等(Ding Yifeng, Chen Haozhong, Lv Ganyun, et al.). 基于Prony算法的谐波和间谐波频谱估计 (Spectrum estimation of harmonics and interharmonics based on Prony algorithm)[J].电工技术学报(Transactions of China Electrotechnical Society), 2005，20(10):94-98.

[15] 李宏(Li Hong)．矩阵特征值问题的若干数值算法研究(Research on some numerical algorithms for solving eigenvalue problem)[D]．广州：华南理工大学(Guangzhou: South China University of Technology)，2011．

Research on fast matrix pencil method for phasor extraction

YANG Yang, XIAO Xiang-ning, CHEN Peng-wei, FANG Zhao

(State Key Laboratory for Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Beijing 102206, China)

Power system monitoring, protection and modal identification rely on the accuracy of phasor parameters, thus quickly and accurately extracting phasor is very important. This paper proposes a fast matrix pencil (FMP) method to estimate parameters of electrical signals based on matrix pencil (MP) method. A square matrix was formed by two time domain coupling matrices of input sampling signals. Its eigenvalues represent the changing information of fundamental and harmonic phasors, as well as the pole information of all components. Under the knowledge of initial phasors, the concerned phasors can be obtained by solving the square matrix eigenvalues. In order to reduce computation burden, this paper uses the Krylov subspace of square matrix to construct a phasor minimal polynomial, which can be used to quickly calculate concerned eigenvalues of specific components. Theoretical analysis and simulation results demonstrate that the FMP method significantly reduces the calculation burden and is simple to conduct as compared with the MP method. It is immune to the effect of non-target components and frequency offset, also could keep a high accuracy with short data window. The method can be applied to the extraction of fundamental phasors, as well as harmonic phasors.

phasor; matrix pencil method; Krylov subspace; minimal polynomial

2015-04-20

中央高校基本科研业务费专项资金资助项目(2015XS22)

杨 洋(1989-)， 男， 河北籍， 博士研究生， 研究方向为电力系统仿真与分析； 肖湘宁(1953-)， 男， 湖南籍， 教授， 博士生导师， 从事电力系统电能质量等方面的教学与科研工作。

TM711

A

1003-3076(2016)02-0001-06