基于风速相关性的风电场群汇聚效应分析

黄大为, 曹康洋永, 张旭鹏

(东北电力大学电气工程学院， 吉林省 吉林市 132012)

基于风速相关性的风电场群汇聚效应分析

黄大为, 曹康洋永, 张旭鹏

(东北电力大学电气工程学院， 吉林省 吉林市 132012)

多个风电场汇聚后的输出功率特性具有明显的汇聚效应，这是处于不同位置风电场风能资源差异性的外在体现。本文运用Copula理论对地理位置相近地区风速的相关性进行量化分析，进行最优Copula函数类型选择以及参数的确定。通过对两两风电场风速相关性的量化分析，提出一种能够反映风电场群输出功率汇聚效应的Monte Carlo模拟方法。在已知风速历史数据的前提下，分析了场间风速含有相关性对风电场群汇集后输出功率特性的影响，从而为风电场群功率外送输电容量规划提供必要的参考。

风力发电； 风电场汇聚效应； 风速相关性； 蒙特卡洛模拟

1 引言

化石能源的过度开采已经造成世界性的能源危机。目前是新型能源高速发展的阶段，风-电转化技术已经成为除水力发电以外可再生能源利用中规模最大、市场竞争力最强、最具发展前景的发电方式之一。风能的大规模开发和利用在调整能源结构、减轻环境污染问题等方面起到了较为突出的作用[1-3]。

我国风电项目的跨越式发展以及特高压战略的展开促使风电基地大规模地联合并网。由于风电场输出功率的特性完全依赖于风速的波动特性，因此在对风电场群进行规划建设时，需考虑风能资源具有的随机性、间歇性对风电场群汇集后功率的整体特性的影响[4-6]。通常对电网进行规划时，利用持续出力特性曲线来描述功率变化规律。对风电场及风电场群外送功率容量进行计算分析是大规模风电并网系统网络规划的重要依据，必须考虑风电场群输出功率的汇聚效应。文献[7]主要基于风电功率历史数据分析得到风电场群输出功率持续出力曲线，并以此为依据建立其外送输电容量的优化模型。由于风电场群存在多个风电场地理位置毗邻的情况，所在地理位置基本处于同一风带，不同风电场的风速之间具有较强的相关性，使得风电场群汇聚后的功率特性与单个风电场输出功率特性差异性较大。国内外学者对风速相关性进行了大量研究工作，最近运用Copula理论分析风场间风速及输出功率相关性的理论及方法较多[8-10]。但这些研究工作均从历史功率数据的统计特性角度进行分析，以此建立风速及风功率相依结构模型。该研究的关键点在于Copula函数的选择以及其函数参数的确定和概率性检验。运用Copula理论可以较好地刻画风场间风速存在的相关特性以及风能资源本身的尾部特性

本文的研究重点在于利用Copula函数对不同风电场风速相关性测度的刻画，分析风电场群输出功率的汇聚效应，提出一种计及风速空间相关性并能够有效反映风电场群输出功率汇聚效应的Monte Carlo模拟方法。

2 风电场群的汇聚效应

对不同规模的风电场汇聚功率的历史统计数据进行分析，其结果表明，多个风电场汇聚之后的功率波动应较单一风电场波动更平缓，等效满发年利用小时数增加，风电场群汇聚后的外送容量也明显低于总装机容量，且随着风电场群汇聚规模的增大，风电功率特性呈现明显的“汇聚效应”[7]。

图1为某地区不同装机规模的风电场群输出功率的持续特性曲线。可以看出，随着风电场群规模的增加，其持续功率特性曲线变得逐渐平缓，最大出力占总装机容量的比例呈现递减趋势。多个风电场汇聚之后的功率特性明显区别于单个风电场的功率特性，其根本原因是不同风电场所在地区风能波动性差异很大。同一时段内，某地区风能充足，风速波动处于波峰段，与之对应的另一地区风能可能不足，风速波动处于波谷段。因此，风电场间的输出功率存在“互济性”。

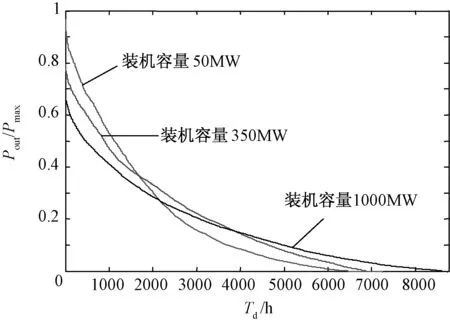
图1 不同装机规模风电场群输出功率的年持续特性曲线Fig.1 Annual wind power duration curves with different integrated wind farms

在对风电场群进行规划设计时，应考虑风电场群的汇聚效应，合理确定规划地区的风电场群的外送容量，并准确地分析风电场群汇聚后接入电网时对电网的影响。

3 计及风场间风速相关性的风电场群输出功率模拟

3.1 基于Copula函数的风速相关性分析

风电场大规模集中并入电力系统是我国风能利用的重要形式。风电场群内存在多个风电场所处的地理位置比较相近的情况，其所在地理位置基本处于同一风带，风电场间的风速波动具有很强的相关性。若忽视这种相关性，可能使与风电并网相关的规划结果出现较大误差，从而增加电力系统的不确定因素，加大电力系统运行风险。因此，借鉴Copula理论对不同风场风速相依关系进行分析，并研究计及风速相关性的风电场群输出功率的Monte Carlo模拟方法具有重要的工程意义。

1959年Sklar定理[10]的提出为Copula理论奠定了基础。Copula函数是将多元随机变量的联合概率分布和其各自的边缘分布相连接的函数，是构建多元随机变量联合分布的有力工具。

假设一个n元随机变量分布函数H(·)的边缘概率分布函数分别为F(x1),F(x2),…,F(xn)，其中x1,x2,…,xn为随机变量，则存在一个Copula函数C(·)满足：

(1)

如果F1,F2,…,Fn是连续的，则Copula函数是唯一确定的，反之亦然。基于该定理可知，当确定了各风场风速的边缘概率分布函数，并确定一个合适的Copula函数后，就可以得出以各风场风速为随机变量的联合概率分布函数。

采用双参数Webiull分布作为风电场风速的概率统计模型[11]。根据地区实测的历史风速数据，求解风速概率分布的参数，由此估算出能直接体现风能资源状况的特性值，为风电场的风电输出功率模拟提供有效数据。双参数Webiull分布概率密度函数为：

(2)

其概率分布函数为：

(3)

式中，c和k分别为双参数Webiull分布的尺度参数与形状参数，尺度参数c反映风电场的平均风速；v为给定的风速(m/s)。

在风速样本充足的条件下，可采用极大似然法数学模型来确定其分布参数，对此文献[11]已有详细论述，此处不再赘述。下面重点对如何运用Copula函数刻画不同风电场风速之间的相关性加以论述。

Copula函数成员广泛，分为两类函数族五种常用函数：属于椭圆Copula函数族的函数为Normal-Copula函数和t-Copula函数；属于ArchimedeanCopula函数族的Copula函数为Gumbel-Copula函数、Clayton-Copula函数和Frank-Copula函数[9]。对上述五种函数的特点和适用范围进行归纳总结，如表1所示。

Copula函数主要有五种类型，下面分别给出其特性与具体表达形式。

(1)Normal-Copula特性：对称分布，不能反映尾部相关性。其表达式为：

表1 五种Copula函数的特性与适应范围

(4)

式中，ρ为相关性系数，这个Copula函数的两个边际分布都是正态分布；积分上限φ-1(x)为标准正态分布函数的逆。

(2)t-Copula特性：对称分布，能反映尾部相关性。其表达式为：

(5)

(3)Gumbel-Copula特性：非对称分布，上尾相关，下尾渐进独立。其表达式为：

(6)

式中，u,v为[0，1]上的均匀分布变量；θ为描述两个变量间相依性关系的参数。

(4)Clayton-Copula特性：非对称分布，下尾相关，上尾渐独立。其表达式为：

(7)

(5)Frank-Copula特性：对称分布，不反映尾部相关性。其表达式为：

(8)

依据Sklar定理以及Copula函数的特性分析，地区风速相关性模型的构造主要分为以下几个步骤。

(1)依据地区实测风速样本，估算风速Weibull分布的参数，确定边缘分布Fi(vi)。

(2)利用适当方法选择适合的Copula函数描述风速变量的相关特性。

(3)估算所选Copula函数的参数。

构建风速相关性模型的关键问题是Copula函数的选择以及Copula函数的参数估算。在风速相关性的研究中，Copula函数的选择要综合以下几个因素考虑：① 所选择的Copula函数其特征能否和实际风场间风速的相关特性相符。②利用该Copula函数对风速进行模拟的结果与现实相符合的程度。③该Copula函数在求解过程中的可操作性。

对于边缘分布函数含有未知参数的情况，可采用两阶段极大似然法对Copula函数的参数进行估算[12]，此处不再赘述。

用上述方法对两两风电场风速间的每类Copula函数进行参数估计，确定Copula的未知参数。最后进行函数的优度检验，确定较优的Copula函数。采用统计分析法，即使用K-S检验法计算检验统计量Z值，其中Z值较小的为最优的Copula函数[13]。Z具体表示为：

(9)

式中，Fn(x)为实际样本数据的经验分布值；G(x)表示Copula函数分布值。

确定了最优的Copula函数及其相关参数后，为生成风速样本，首先求取Weibull随机风速模型的累积分布函数的反函数。然后根据MonteCarlo模拟方法产生一组服从[0，1]均匀分布的随机数。最后依据这组MonteCarlo抽样选择出的随机数的反函数模型和两个风电场风速的联合概率分布模型模拟出两个风速的样本。

图2为依据两地区风速的实测数据，考虑风速空间相关性的MonteCarlo模拟。由图可见，两地区模拟风速集中分布在45°对角线上，表明两地区风速的相关关系较强。过去对风电场群进行规划分析时，将各地区风速看成是独立变量并不能反映真实的地区间风速关系。

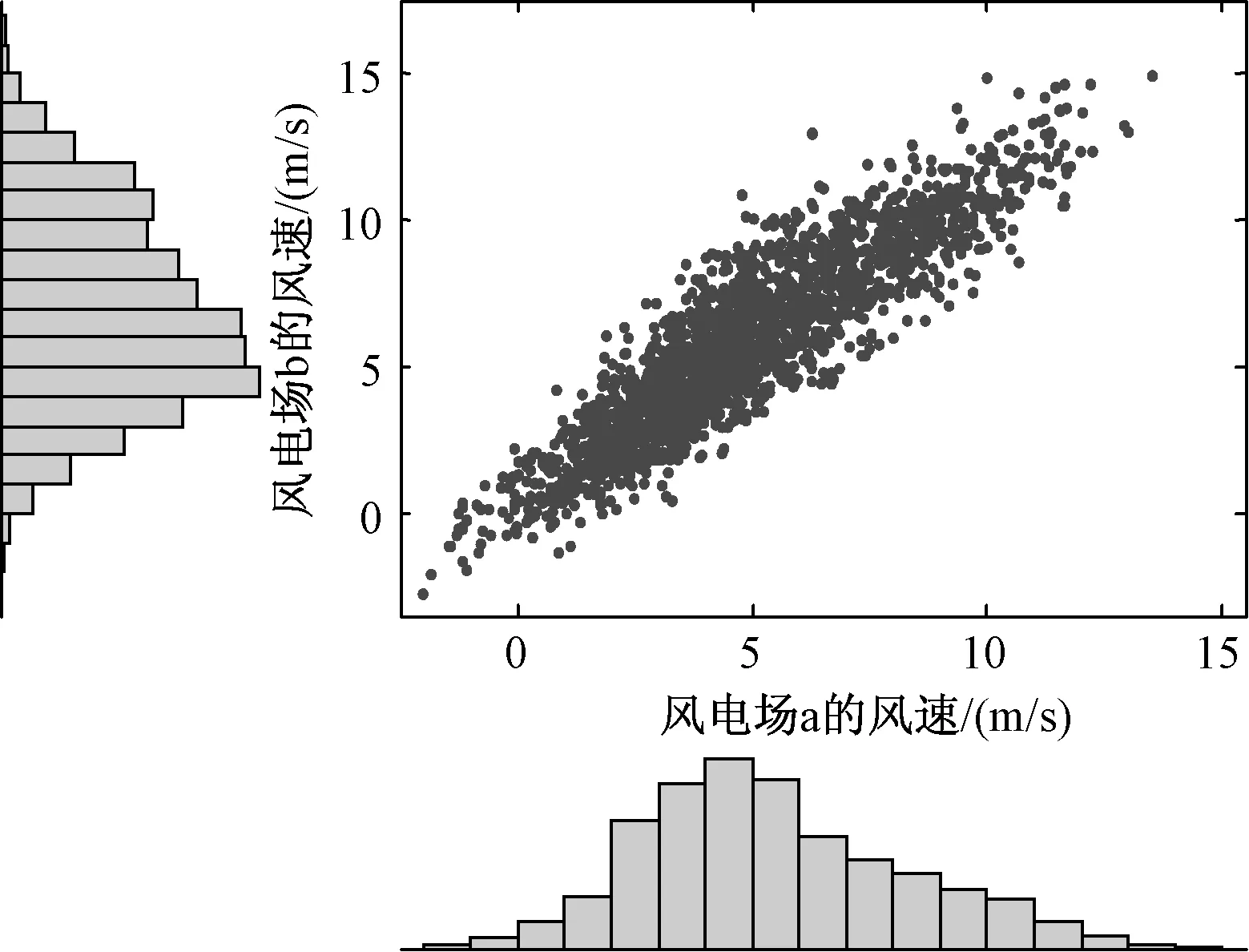
图2 两相邻风电场风速相关性的Monte Carlo模拟Fig.2 Correlation of wind speed Monte Carlo simulation of adjacent wind farms

3.2 基于Copula理论的反映风电场群功率汇聚效应的模拟方法

在风速的Weibull分布模型以及Copula函数模型的基础上模拟风电场小时风速值。利用风速与风电机组出力的函数关系得到风电场的功率输出情况。现阶段研究表明风电机组的功率输出有三种模型:线性模型，二次方模型，三次方模型。但是文献[14]指出线性模型和三次方模型对风机的功率输出描述并不准确。因此本文采用二次方模型，功率输出表达式为：

(10)

式中，P(vwt)为风力发电输出功率，MW；Pr、vci、vr和vco分别为风力发电机额定功率、切入风速、全额风速和切出风速；a、b和c为估计参数，其值取决于Pr、vci、vr和vco[15]。公式中参数的具体数值与风电场中各个风电机组的型号以及参数有关。

基于Copula理论的风电场群输出功率的MonteCarlo模拟方法具体步骤如下。

(1)依据地区的测量风速数据构建各风电场风速的边缘分布，确定其Weibull分布的参数。

(2)依据两两风电场的历史风速数据确定不同的Copula函数参数并对函数进行优选，确定合适的Copula函数作为描述各变量间相关结构的依据。

(3)进行反映两两风电场风速相关性的MonteCarlo模拟，并根据各风电场风机型号参数，利用式(10)得到各风电场输出功率序列。

(4)将模拟生成的各风电场输出功率按相应的模拟序列求和，即得到反映风电场间风速相关性的风电场群输出功率模拟数据序列。

(5)将风电场群输出功率的模拟序列按从大到小的顺序重新排列，生成反映风电场群功率汇聚效应的持续功率特性曲线。

4 算例分析

从吉林省气象数据库中选择地区风速数据作为研究样本，进行基于风速相关性的风电基地汇聚功率特性分析。该风电场群拟建设8个风电场，其中风场2、3、4地理位置较为相近，风场7、8地理位置较为相近。具体参数如表2～表4所示。

表2 风电场风机型号及风电场的额定功率

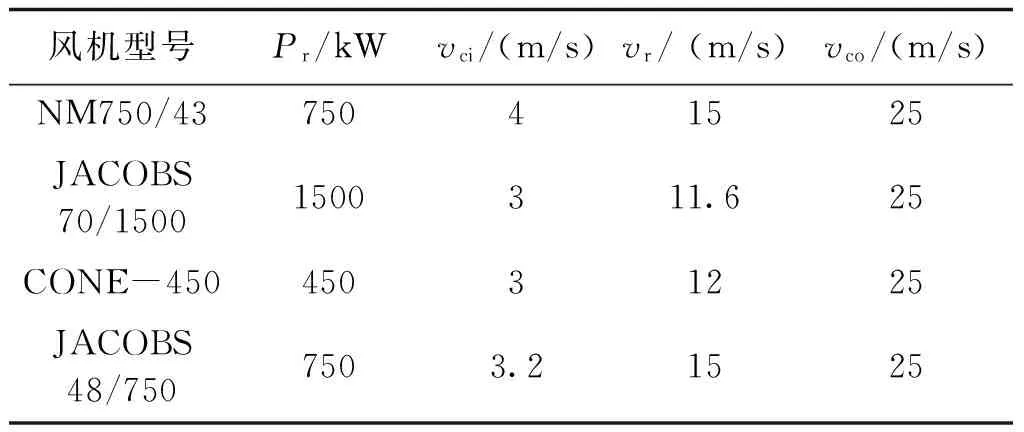
表3 风电机机型的技术参数

基于上述给定数据，为了给风电基地的规划建设提供有效依据，现进行风电场群汇集功率模拟。首先，对位置相近地区进行两两风电场间的风速空间相关性分析，选择较优的Copula函数进行一年内风速的Monte Carlo模拟。其他地区采用双参数Weibull分布风速模型模拟一年内风电场风速值。根据已有地区风速模拟数据，利用风速与风电机组出力的函数关系，确定各个风电场出力情况。通过风电场群汇聚后的持续出力曲线，分析风电场群整体外送功率特性。

图3为总装机容量为350MW的风电场群模拟持续出力曲线。分析表明，考虑风速空间相关性后，风电场群的汇聚总功率特性与未考虑时有显著区别，持续出力曲线更为平缓，最大出力占总装机容量的比例明显下降(由0.87Pmax下降到0.74Pmax)，而风电场群等效满发年利用小时数增加，模拟等效满发年利用小时数递增(由1720h增长到1972h)。

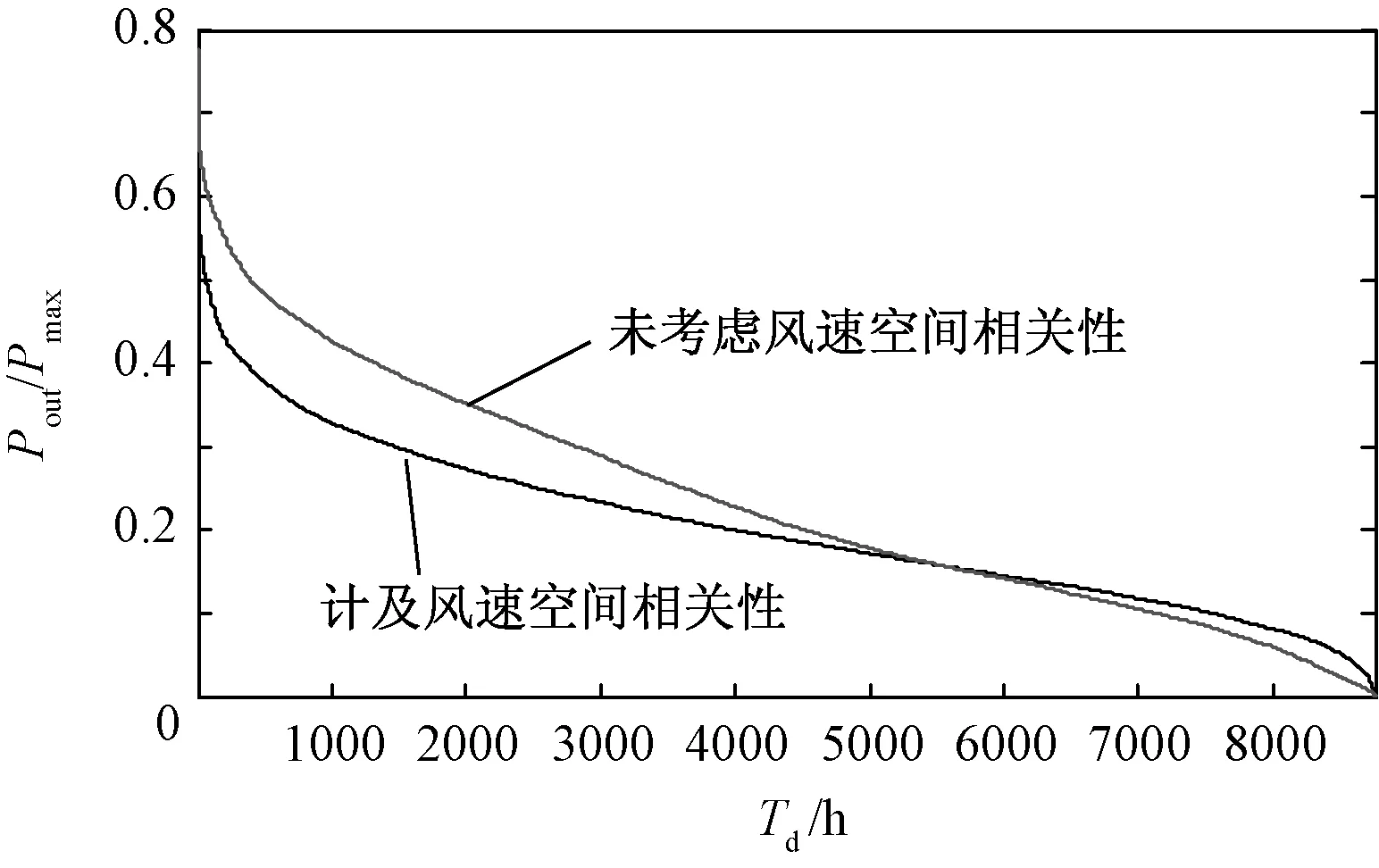
图3 考虑风速相关性的风电场群持续出力模拟曲线Fig.3 Simulation curves of wind farm group of continuous output considering wind speed correlation

可见，对风电场群进行规划分析时，将各地区风速看成是独立变量并不能反映真实的地区间风速关系，依此进行的风电场群规划有明显不足。

5 结论

对Copula 函数的探究可以追溯到20世纪50年代，但将Copula 函数真正应用于风电系统领域的研究正处于起步阶段。Copula 函数具有许多优良的统计特性，近几年来得到了广泛的应用，已经成为多元分布建模的一个重要工具。本文提出了基于Copula理论的反映风电场群输出功率汇聚效应的模拟方法，对地理位置毗邻地区的风速存在的相关特性进行刻画。本文分析表明，计及风速相关性的风电场群的年持续出力特性曲线趋于平缓，其所反映的汇聚效应更加明显。

在风电场群规划和风电场群外送输电容量计算中，采用本文方法估算风电场群年持续出力曲线，可在一定程度上体现风电功率的时空分布规律。由于本文主要研究风电场之间风速相关性对风电场群功率汇聚效应的影响，在模拟计算中未计及风电场内风电机组风速相关性对其汇聚效应的影响，因此所得结果可能偏于保守。

[ 1] 谭忠富, 鞠立伟 (Tan Zhongfu, Ju Liwei). 中国风电发展综述：历史、现状、趋势及政策 (Review of China’s wind power development: History, current status, trend and policy) [J]. 华北电力大学学报(Journal of North China Electric Power University), 2013，(2)：1-7.

[ 2] 罗如意, 林晔, 钱野 (Luo Ruyi, Lin Ye, Qian Ye). 世界风电产业发展综述 (The development and prospects of world wind power industry) [J]. 可再生能源 (Renewable Energy Resources), 2010，28(2)：14-17．

[ 3] 沈又幸, 郭玲丽, 曾鸣 (Shen Youxing, Guo Lingli, Zeng Ming). 丹麦风电发展经验及对我国的借鉴 (Wind power development experience of Denmark and its reference to China) [J]. 华东电力 (East China Electric Power), 2008，36(11)：153-157．

[ 4] 张节潭, 程浩忠, 黄微, 等 (Zhang Jietan, Cheng Haozhong, Huang Wei, et al.). 含风电场的电源规划综述 (Review of generation expansion planning for power system with wind farms) [J]. 电力系统及其自动化学报 (Proceedings of the CSU-EPSA), 2009，21(2)：35-41．

[ 5] 高赐威, 何叶 (Gao Ciwei, He Ye). 考虑风力发电接入的电网规划[J] (Research of electric network planning with wind power integration considered) [J]. 电力科学与技术学报 (Journal of Electric Power Science and Technology), 2009，24(4)：19-24．

[ 6] 孙元章, 吴俊, 李国杰, 等 (Sun Yuanzhang, Wu Jun, Li Guojie, et al.). 基于风速预测和随机规划的含风电场电力系统动态经济调度 (Dynamic economic dispatch considering wind power penetration based on wind speed forecasting and stochastic programming) [J]. 中国电机工程学报 (Proceedings of the CSEE), 2009，29(4)：41-47．

[ 7] 穆钢, 崔杨, 严干贵 (Mu Gang, Cui Yang, Yan Gangui). 确定风电场群功率汇聚外送输电容量的静态综合优化方法 (A static optimization method to determine integrated power transmission capacity of clustering wind farms) [J]. 中国电机工程学报(Proceedings of the CSEE), 2011，31(1)：15-19．

[ 8] 蔡菲, 严正, 赵静波, 等 (Cai Fei, Yan Zheng, Zhao Jingbo, et al.). 基于Copula理论的风电场间风速及输出功率相依结构建模 (Dependence structure models for wind speed and wind power among different wind farms based on Copula theory) [J]. 电力系统自动化(Automation of Electric Power Systems), 2013，37(17)：9-16．

[ 9] 季峰, 蔡兴国, 王俊 (Ji Feng, Cai Xingguo, Wang Jun). 基于混合Copula函数的风电功率相关性分析 (Wind power correlation analysis based on hybrid Copula) [J]. 电力系统自动化 (Automation of Electric Power Systems), 2014, 38(2): 1-5,32．

[10] 简金宝, 刘思东 (Jian Jinbao, Liu Sidong). 风速空间相关性和最优风电分配 (Wind speed spatial correlation and optimal wind power allocation) [J]. 电力系统保护与控制 (Power System Protection and Control), 2013,41(19): 110-116．

[11] 龚伟俊, 李为相, 张广明 (Gong Weijun, Li Weixiang, Zhang Guangming). 基于威布尔分布的风速概率分布参数估计方法 (The estimation algorithm on the probabilistic distribution parameters of wind speed based on Weibull distribution) [J]. 可再生能源 (Renewable Energy Resources), 2011，29(6)：20-23．

[12] 张义斌, 王伟胜 (Zhang Yibin, Wang Weisheng). 风电场输出功率的概率分布及其应用 (Probability distribution of power output for wind power field and its application) [J]. 电力设备 (Electrical Equipment), 2004, 5(8): 38-40．

[13] Wang X, Makis V. Autoregressive model-based gear shaft fault diagnosis using the Kolmogorov-Smirnov test [J]. Journal of Sound and Vibration, 2009，327(3)： 413-423．

[14] 陈树勇, 戴慧珠, 白晓民, 等 (Chen Shuyong, Dai Huizhu, Bai Xiaomin, et al.). 风电场的发电可靠性模型及其应用 (Reliability model of wind power plants and its application) [J]. 中国电机工程学报 (Proceedings of the CSEE), 2000，20(3)：27-30．

[15] Giorsetto P, Utsurogi K F. Development of a new procedure for reliability modeling of wind turbine generators [J]. IEEE Transactions on Power Apparatus and Systems，1983，PAS-102(1)：134-143．

Clustering effect analysis of wind power stations based on correlation of wind speed

HUANG Da-wei, CAO Kang-yang-yong， ZHANG Xu-peng

(School of Electrical Engineering, Northeast Dianli University, Jilin 132012, China)

The output power of multiple wind farms has obvious clustering effect, which is the external characteristic of the wind energy resources diversity at different positions. In this paper the Copula theory is used to quantify and analyze the relativity of wind speed which has geographical proximity, and the optimal copulas function is selected and the parameters are determined. Through the quantification of the correlation of the two wind farms’ speed, a Monte Carlo simulation method which can reflect the output power clustering effect of wind farms is proposed. With the known historical data of the wind speed, the influence of wind speed correlation to the output power characteristics of wind farms is analyzed. The results are important reference to transmission capacity programming for the wind farm group power output.

wind power generation; clustering effect of wind generations; correlation of wind speed; Monte Carlo simulation

2015-01-22

吉林省科技发展规划项目(20130102026JC)

黄大为 (1976-), 男, 黑龙江籍， 副教授, 博士, 主要从事电力系统运行与控制、 新能源并网及高效利用方面的研究; 曹康洋永 (1989-), 男, 吉林籍， 硕士研究生, 主要研究方向为电力系统运行与控制。

TM71

A

1003-3076(2016)02-0018-06