基于停电性质分类的多环节电网可靠性评估方法

郑文杰，黄嘉健 ，孙 川，汪隆君

（1.广东电网公司电力科学研究院 广东省智能电网新技术企业重点实验室，广东 广州 510080；2.华南理工大学 电力学院，广东 广州 510640）

0 引言

随着社会经济发展和生活水平提高，业界和用户对供电可靠性的要求越来越高。可靠性管理作为行业监督管理和用户服务的重要内容，在促进电力企业加强设备管理、技术管理等方面具有极其重要的意义［1］。目前，电网可靠性管理按照工作流程可分为下达分解、落实管控和考核总结三部分。实践中常出现以下问题：在考核总结时，往往将可靠性指标任务难以完成的原因直接归结于脆弱的网架结构和落后的管理手段；可靠性分析的内容十分有限，缺少对电网管理水平、运维水平的关联分析，更无法有针对性地指导增强性措施的开展。值得注意的是，电力系统可靠性是由电源向负荷经过输电网、配电网等多环节逐级传递，最终通过供电可靠性指标来表征。为进一步提高电网公司可靠性精益化管理水平，有必要研究多环节电网可靠性评估方法。

按照电网停电性质划分，可分为故障停电和预安排停电，系统平均停电时间指标则为故障停电时间与预安排停电时间之和［2］。故障停电是设备随机故障引起的，在电网结构、设备可靠性、运行环境等条件确定的情况下，其可控性不强。经过多年发展，配电网故障停电可靠性评估方法可分为解析法和蒙特卡洛模拟法［3］，它们多假定配电网电源完全可靠，对配电设备故障造成的后果进行分析，基于状态与后果的加权和获得可靠性指标。输电网规划阶段必须进行N-1校核，然而运行阶段类似深圳“4·10停电”和东莞“4·12停电”等由输电网引起的停电事件时有发生。由于计算规模限制，现有可靠性评估研究大多考虑了本环节电网安全约束和随机故障，忽略了上一环节电网的随机故障［4］。这样处理忽略了输电网故障对供电可靠性的影响，将造成配电网可靠性评估结果偏乐观。以等效负荷削减为后果形成的输电网可靠性评估指标体系［4］，不直观且不易验证，在工程界备受争议。文献［5-6］分别定义了传输点DP（Delivery Point）指标及基于DP的输电网可靠性指标，直观反映输电网可靠性水平，但均未进一步拓展至供电可靠性。

预安排停电指电网公司为提高电网及设备安全运行水平，预先做计划获调度批准后调整运行方式而导致的部分区域停电，其不仅与电网及其设备安全运行水平等有关，还与运行管理因素紧密相关，具备一定的可控性。根据广东电网近年停电事件的数据统计，预安排停电时间占停电总时间的60%以上［7］，预安排停电时间的合理控制是可靠性指标管理的关键。为快速有效地提高供电可靠性水平，电网企业应优化生产管理流程，加强管控预安排停电时间，在尽力实现预安排停电可靠性指标的逐年纵向改进的同时，还应参与同行业的横向对标。目前对预安排停电建模主要有2种方案：折算法，将预安排停电率与投资或故障停电率等单一因素按一定比例折算；测算法［7］，根据具体停电计划建立不同工程类型的预安排停电模型测算预安排停电率。前者工程可操作性强，但不利于预安排停电指标管控水平的提升；后者需要数据多，计算难度高，且指标下达之初难以获得预安排停电时电网运行方式，工程可操作性欠佳。

为更加准确地评估电网可靠性、提高电网公司可靠性精益化管理水平，提出基于停电性质分类的多环节电网可靠性评估方法；采用输电网与配电网的连接点CP（Connection Point）建立多环节电网供电可靠性联系，通过可靠性网络等值方法量化输电网故障对供电可靠性指标的影响；基于条件数诊断电网生产管理控制指标的多重共线性，采用岭迹图筛选出主要电网生产管理控制指标、确定岭参数值，通过岭回归（ridge regression）分析量化管理控制指标对预安排停电可靠性指标的影响。以广东电网公司所辖某供电局2013年供电可靠性评估为算例，对所提模型及方法进行了验证。

1 多环节电网故障停电可靠性评估

1.1 连接点可靠性指标及其评估

处于输电网末端的终端变电站，其降压变压器的低压侧母线（以下简称低压母线）是输配CP，也是电力资产管辖边界。低压母线停电必将对供电可靠性指标造成直接影响，即输电网故障对供电可靠性的影响是通过终端变电站低压母线施加的。导致低压母线停电的原因按照停运发生位置可分为2类：终端变电站的电源进线停运，包括非计划停运和受累停运；终端变电站内主设备非计划停运。其中，终端变电站电源进线的非计划停运状态指设施处于不可用而又不是计划停运的状态；受累停运指设施本身可用，因相关设施的停运而被迫退出运行状态，包括了由终端变电站外输电系统设备故障导致进线停运的情况。

以低压母线为输配CP，定义基于CP的可靠性指标，分为连接点级指标和系统级指标。连接点级指标不仅是求解系统级指标的基础，还是电网故障停电可靠性评估的核心内容，包括平均停运频率λCP和平均停运时间dCP。其中，λCP表示统计时间范围内CP的平均停运次数；dCP表示统计时间范围内CP的平均停运时间。

系统级指标包括变电站平均停运频率rSAIFI-S和平均停运时间rSAIDI-S、输电网平均停运频率rSAIFI-T和平均停运时间rSAIDI-T，它们的定义为：

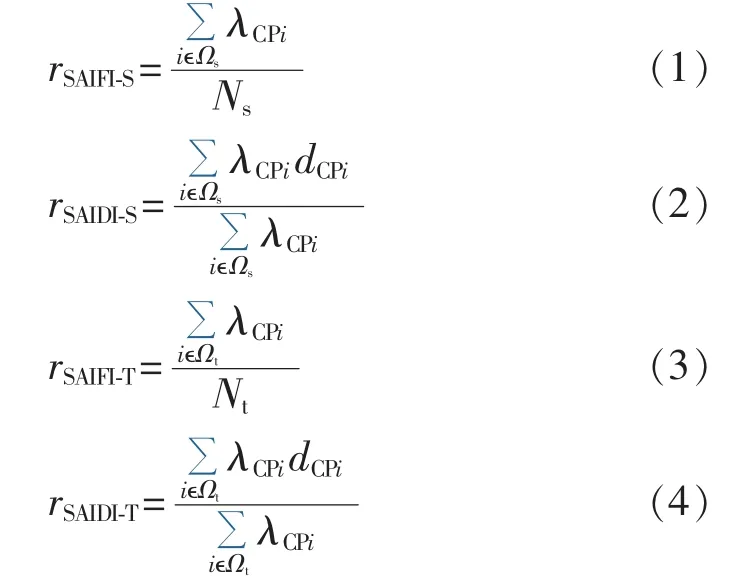
其中，λCPi和dCPi分别为连第i个CP（下文用CPi表示）的平均故障频率和平均故障时间；Ωs和Ωt分别为变电站和输电网中CP构成的集合；Ns和Nt分别为变电站和输电网中CP的数量。

为便于工程应用，基于CP可靠性指标的评估方法的步骤如下。

a.范围界定。评估范围界定为从终端变电站的电源进线到输配CP的电气主接线。

b.可靠性建模。对电源进线和站内电气设备建立相应的可靠性模型，可采用经典的2状态停运模型［4］，即设备状态仅处于运行和停运2种状态。

c.可靠性评估。基于故障后果模式分析FMEA（Failure Mode and Effects Analysis）［8］法进行可靠性评估。

d.指标计算。计算CP、变电站、输电网可靠性指标。

上述方法仅需要收集终端变电站主接线拓扑结构、终端变电站电源进线和站内电气设备的非计划停运率及其平均停运时间等。而以上数据统计属于《输变电设施可靠性评价规程实施细则》的日常工作，不需增加额外工作量，更不需要可能影响电网安全稳定运行的敏感数据，如传统输电网可靠性评估所需的输电网拓扑结构及电气参数；所获系统级指标概念直观，易于统计，便于验证，从供电连续性角度深化了输电网可靠性评估的分析应用。

1.2 计及输电网故障的供电可靠性评估

从可靠性网络等值法原理［9］可知，配电网可靠性评估包括向上等效及向下等效2个过程。由于终端变电站馈线电源侧配有继电保护装置，能快速隔离馈线故障，因此馈线故障一般不会造成变电站低压母线停运，可忽略向上等效过程；而在向下等效的过程中，将变电站低压母线对馈线的影响用一个串在馈线首端的等效元件来代表。作为CP的低压母线，其可靠性基础数据在1.1节中已获得。

对于辐射状馈线，评估步骤与传统方法［1，3，10-11］评估步骤基本相同；下面具体阐述计及输电网故障的环网接线供电可靠性评估步骤。

馈线Fi的系统平均停电持续时间指标为：

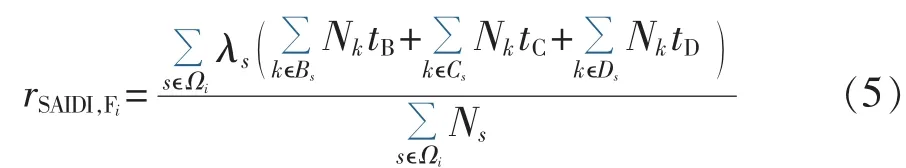
其中，Ωi为馈线Fi最小隔离区的集合；λs为最小隔离区 s的平均停运频率；Bs、Cs、Ds分别为最小隔离区s故障时B类、C类、D类区域的集合；Nk为区域k内的用户数；tB、tC、tD分别为故障隔离平均时间、联络开关倒闸平均时间、故障修复时间；Ns为区域s内的用户数。

当CP下接的配电网连成环网时，根据主电源和备用电源异同情况，抽象为2种典型结构。

a.馈线 Fi、Fj分别通过断路器与 CPi、CPj相连，且2条馈线末端经联络开关相连，其拓扑如图1（a）所示。以馈线Fi为例，其主电源为Sm，与CPi直接连接，其备用电源Sa经馈线Fj后与CPj相连。

b.馈线Fi、Fj均通过断路器与CPi相连，其拓扑如图 1（b）所示。

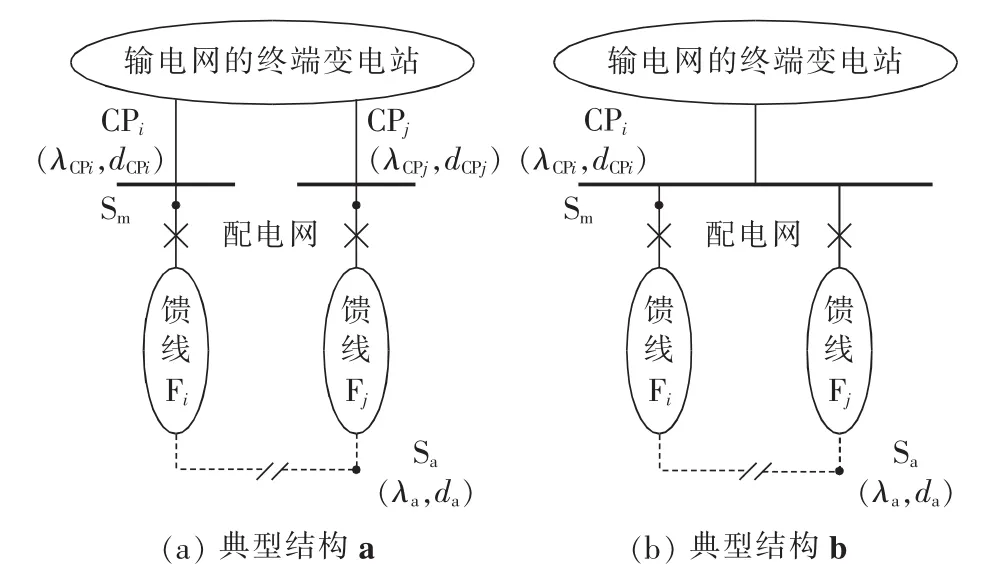
图1 环网拓扑结构Fig.1 Topology of loop network

图1（a）中，馈线 Fi的备用电源点 Sa是馈线 Fj末端与联络开关相连的节点，Sa的平均停运率λa和年平均停运时间ta分别为：

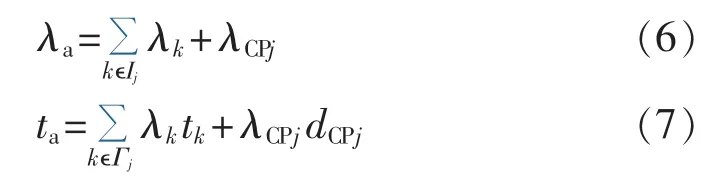
其中，Γj为馈线Fj中导致Sa停电最小隔离区集合；tk为最小隔离区k故障造成Sa停电时间。若统计时间为1 a，则备用电源不可用率λAa为：

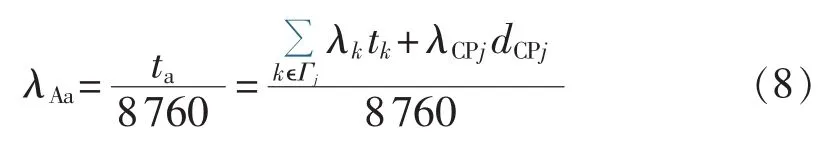
当馈线故障时，若备用电源可靠，故障下游负荷点的停电时间为联络开关倒闸平均时间tC；若备用电源失效，则转供电失败，故障下游负荷点的停电时间为故障修复时间tD。基于全概率公式，此时C类区域停电时间的修正值为：

式（9）将备用电源的不可靠性转化为负荷停电时间的不确定性。

计及输电网故障的馈线Fi的系统平均持续停电时间指标修正为：

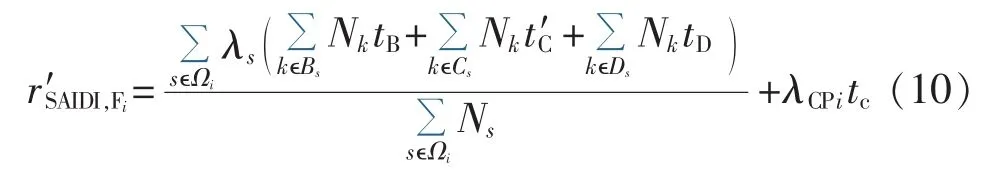
图1（b）中，由于馈线 Fi和 Fj的电源皆取自 CPi。当CPi故障时，馈线Fi、Fj同时停电，此时备用电源Sa亦处于停电状态，无法实现对馈线Fi转供电，即此时不存在C类区域。计及输电网故障的馈线Fi的系统平均持续停电时间指标修正为：

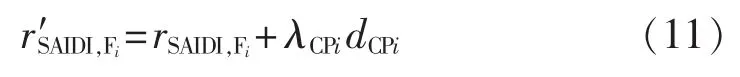
馈线Fi其他可靠性指标的计算方法与系统平均持续停电时间类似，在此不再赘述。应用上述方法的关键在于2点：计算开环方式下备用电源的可靠性参数；故障后果分析时甄别备用电源是否同时处于失效状态。

2 多环节电网预安排停电可靠性评估

可靠性指标与网络拓扑、设备可靠性参数、开关类型和位置有关，而可靠性指标灵敏度分析所得结论非常有限，且分析对象仅限于配电网，缺少可靠性指标对电网管理水平、运维水平的关联分析，更无法有针对性地指导增强性措施的开展。注意到电网公司日常运行管理已形成一套概念直观、易于统计且在行业内已达成共识的电网生产管理控制指标，若能与预安排停电可靠性指标建立某种函数关系，无疑开辟了一条新的可靠性管理思路，不仅能评估预安排停电可靠性指标，指导具体增强性措施的开展，还能激励电网企业提升可靠性管理水平，在电网企业内部形成促进可靠性提升的良性循环机制。

基于以下原则梳理筛选南方电网公司的管控指标：

a.选用信息系统中有统计的指标；

b.剔除统计口径模糊的指标；

c.选用统计周期精确到月的指标。

构建预安排停电可靠性指标与管控指标的关系，如图2所示。这些指标大致分为5个方面，分别是负荷供应能力、网络结构水平、运行管理水平、装备技术水平、基建技改投资。显然，这些指标都与预安排停电的实施有着密切关系，其指标数据获取和信息采集工作较为方便，容易量化并以月为单位滚动监测。

图2 预安排停电可靠性指标与管控指标的关系Fig.2 Relationship between scheduled outage reliability index and management control index

设自变量X表示各管控指标，因变量y表示预安排停电可靠性指标，采用多元线性回归即可拟合出两者之间的数学表达式，建立预安排停电可靠性指标和管控指标的经验函数关系，以便量化管控指标对预安排停电可靠性指标的影响。

管控指标不可避免地存在统计口径相似或内容相关，造成管控指标之间存在多重共线性。此时若采用常规最小二乘估计作回归拟合将导致回归系数估计值方差大、稳定性差，模型精确度低，且回归系数正负号可能出现倒置的情况，使得无法对回归方程进行合理解释，极大降低回归模型的实用价值［12-14］。

为减少管控指标多重共线性导致回归模型失真的问题，确保回归模型的有效性，首先应利用条件数法对管控指标之间的多重共线性进行诊断。设选定电网公司的p个管控指标，其构成矩阵X：

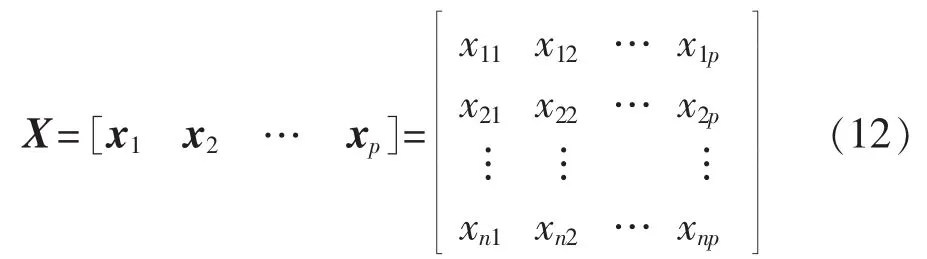
方阵XTX的条件数定义为：

其中，λmax和λmin分别为方阵XTX的最大和最小特征根。条件数度量了XTX的特征根散布程度，可以用其判断多重共线性是否存在及其严重程度。实践中，若0＜Cd＜100，则认为不存在多重共线性；若100≤Cd≤1 000，则认为存在较强的多重共线性；若Cd＞1000，则认为存在严重的多重共线性［15］。

设y与X之间的多元线性回归模型为：

其中，β为回归系数构成的列向量；ε为误差项。

常规最小二乘估计法的回归系数列向量为：

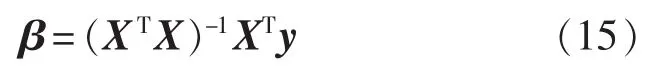
当诊断发现管控指标存在较为严重的多重共线性时，，常规最小二乘法法失效。而岭回归估计方法［16］则是给XTX附加一个正的常数矩阵kI（k＞0，I为单位矩阵），使矩阵 XTX+kI的奇异程度大幅降低，其回归系数列向量为：

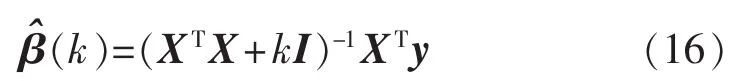
当k=0时，岭回归估计回归系数（0）等于常规最小二乘估计所得β。当岭参数k在（0，+∞）内变化时，回归系数（k）为 k 的函数，作出（k）的变化曲线，即岭迹。通过对岭迹的分析［15］，可对管控指标做进一步的判定和筛选，并确定合适的岭参数k值。岭参数的确定原则为：岭参数取值应尽可能小，使岭迹趋于稳定。将岭参数代入式（14），即可得到更加稳定的回归系数估计，从而减少管控指标多重共线性的影响。

综上所述，基于岭回归分析评估预安排停电可靠性指标的方法如下：

a.基于条件数作多重共线性诊断；

b.采用岭迹图筛选出主要电网生产管理控制指标，并确定岭参数值k；

c.将样本数据的管控指标和预安排停电可靠性指标代入已确定k的式（16），获得各管控指标的回归系数；

d.把回归系数和待估数据的管控指标值代入式（14），求预安排停电可靠性指标估计值。

3 多环节电网可靠性评估流程

基于以上理论，可得基于停电性质分类的多环节电网可靠性评估流程如图3所示。

图3 多环节电网可靠性评估流程Fig.3 Flowchart of reliability evaluation for multi-level power grid

4 算例分析

以广东电网公司所辖某供电局2013年供电可靠性的平均停电持续时间指标评估为算例，验证所提模型以及方法。基于传统配电网可靠性评估法可以求得不考虑输电网故障的平均停电持续时间为1.743h/（户·a），基于本文所提模型及方法求得计及输电网故障的平均停电持续时间为1.789 h/（户·a），输电网故障停电时间占总停电时间的2.57%。2013年该供电局故障停电造成的用户平均停电时间统计值为1.83 h，输电网故障停电时间占总停电时间的2.22%。可见本文模型故障停电可靠性指标评估值与实际统计值十分接近，相对误差小于5%。进一步地，忽略备用电源不可靠及同一低压母线作为电源的情况，计及输电网故障的平均停电持续时间为1.788 h/（户·a）。可见，所提方法能有效量化输电网故障对故障停电可靠性指标的影响。

下面验证所提预安排停电时间评估方法的有效性和可行性。基于所提原则选出电网公司管控指标：基建技改投资额x1、变电站重过载率x2、线路重过载率x3、配变重过载率x4、延时送电率x5、单线单变率x6、自动化覆盖率x7、带电作业率x8、配网线路分段数x9、配网线路线径不满足率x10、配网线路环网率x11和配网线路可转供率x12等，并设y表示预安排平均停电持续时间。以广东电网公司所辖18个地级供电公司2013年数据为样本，对余下1个地级供电公司的预安排平均停电持续时间进行评估，并与实际统计值作对比分析。此时样本数n=18，管控指标数p=12。

首先基于条件数作多重共线性诊断，计算方阵XTX 的特征根，得 λmax=186.8626，λmin=0.0004，此时Cd=467156，远大于1000，说明管控指标存在严重的多重共线性。

通过岭迹分析筛选管控指标。令岭参数k从0增加至0.4，步长设为0.001，部分管控指标的回归系数岭迹如图4所示，包括延时送电率x5、配网线路分段数x9、配电网线路环网率x11和配电网线路可转供率x12的回归系数所对应的岭迹曲线。

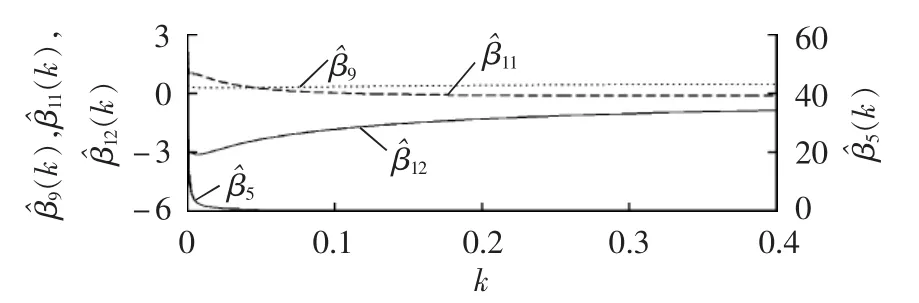
图4 部分管控指标的回归系数岭迹Fig.4 Ridge trace curve of regression coefficient for some management control indices

由图4可得以下结论。

a.在岭参数 k=0 时，5（k）数值很大；k 略微增加，5（k）迅速趋于 0，并且稳定下来。这表明：延时送电率对预安排平均停电持续时间的影响很小，可将其剔除。若采用常规最小二乘法，则会夸大延时送电率的影响。

b.在 k=0 附近，11（k）骤然降低，12（k）急速增加，两者变化剧烈，两者之和在 kϵ（0，0.4］范围内大体上平稳，这反映出可转供率与环网率存在显著的线性相关性，这与工程实际相符。岭回归分析时，强相关的管控指标仅需保留1个。又注意到11（k）随k值增加由正值变为负值，而环网率越高平均停电持续时间越小，其回归系数不应为正；12（k）不受 k 变化影响均为负值，与工程实际相符。因此，剔除环网率，保留可转供率。

c.9（k）不受 k 变化影响保持为正值，而配网线路分段数越多供电可靠性越高，平均停电持续时间越小，其回归系数不应为正，即回归系数符号与工程实际并不相符，因此剔除线路分段数。

至此，通过岭迹图剔除了多余和不合理的管控指标，余下9个管控指标分别为：投资总额x1、变电站重过载率x2、线路重过载率x3、配变重过载率x4、单线单变率x6、自动化覆盖率x7、带电作业率x8、配网线路线径不满足率x10和配网线路可转供率x12。计算筛选后方阵XTX的特征根，求得此时的条件数Cd=3196，这说明保留管控指标的多重共线性有所降低，但依然还存在。为此对岭迹图作进一步分析以确定合适的岭参数。

将筛选后管控指标的岭迹图绘于图5，由图5可见：随着k的增大，9条岭迹趋于稳定，且在k≥0.3后，岭迹基本保持不变。根据岭回归理论和岭参数确定原则，取k=0.3。

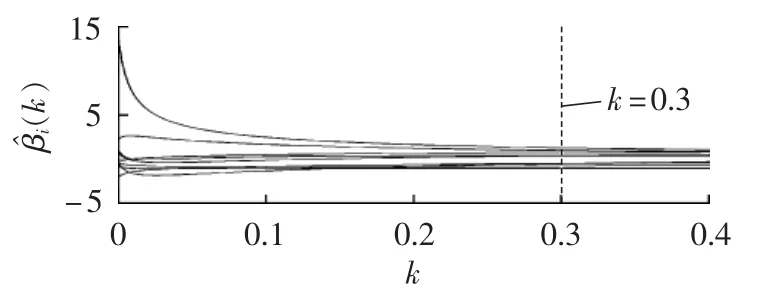
图5 岭参数的确定Fig.5 Determination of ridge parameters

将岭参数值代入式（16）作岭回归，并与常规最小二乘法结果进行比较。岭回归方程为：

若直接采用常规最小二乘法所获回归方程为：

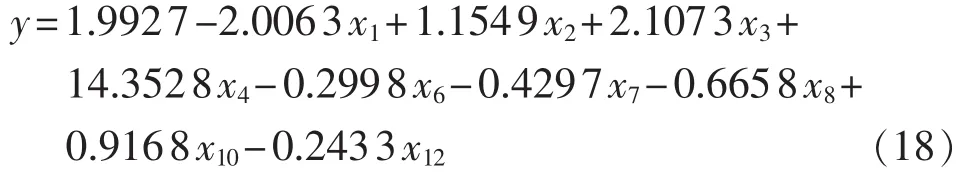
从式（17）和式（18）可见，2 种方法拟合出的回归系数存在较大区别。为检验回归方程的合理性，将所余供电局的管控指标数据代入岭回归方程，绘出随岭参数k变化的曲线见图6。2013年该供电局预安排停电时间的实际统计值为2.95 h，在图6中以虚线标识。式（17）估计预安排停电时间为3.04 h；式（18）所获常规最小二乘法估计结果为2.15 h，与岭参数k=0时的岭估计结果相等。由于管控指标存在多重共线性，常规最小二乘法估计所拟合结果严重偏离实际统计值，且回归系数β6为负值，即单线单变率越高供电可靠性越高，不符合工程实际，可见常规最小二乘法实用价值较低；合适岭参数的岭估计所拟合结果在实际统计值附近，这是由于岭回归估计有效降低了管控指标多重共线性的影响，效果优于常规最小二乘法，其回归系数还量化了管控指标对预安排停电可靠性指标的影响。

图6 岭估计法和常规最小二乘估计法的结果比较Fig.6 Comparison of results between ridge estimation and least square estimation

5 结论

本文提出了基于停电性质分类的多环节电网可靠性评估方法。该方法基于输配CP和可靠性网络等值方法量化输电网故障对故障停电可靠性指标的影响；基于岭迹图和岭回归分析量化管控指标对预安排停电可靠性指标的影响。算例分析表明：所提模型及方法能更加精准地评估电网可靠性指标，有助于提高电网公司可靠性精益化管理水平。

样本数量增加有助于提高预测的准确性，减少样本不足导致的模型误差。因此，后续将研发电网可靠性评估辅助分析系统，与地理信息系统（GIS）平台、营配一体化平台等相关信息系统接口，实现数据自动导入，滚动预测电网公司可靠性指标，横向/纵向促进电网公司可靠性管控水平提升。

［1］邱生敏，管霖.规划配电网简化方法及其可靠性评估算法［J］.电力自动化设备，2013，33（1）：85-90.QIU Shengmin，GUAN Lin.Simplification of distribution network planning and its reliability evaluation algorithm［J］.Electric Power Automation Equipment，2013，33（1）：85-90.

［2］国家能源局.供电系统用户供电可靠性评价规程：DL/T836—2012［S］.北京：中国电力出版社，2012.

［3］赵华，王主丁，谢开贵，等.中压配电网可靠性评估方法的比较研究［J］.电网技术，2013，37（11）：3295-3302.ZHAO Hua，WANG Zhuding，XIE Kaigui，etal.Comparative study on reliability assessmentmethodsformedium voltage distribution network［J］.Power System Technology，2013，37（11）：3295-3302.

［4］LI W.Risk assessment of power systems：models，methods and applications［M］. ［S.l.］：IEEE Computer Society Press，2005.

［5］Task Force Member.Reporting bulk power system delivery point reliability［J］.IEEE Trans on Power Systems，1996，11（3）：1262-1268.

［6］张蓓，张焰，李力，等.基于连接点的输电系统可靠性统计评价方法［J］.电力自动化设备，2012，32（3）：76-80.ZHANG Bei，ZHANG Yan，LI Li，et al.Reliability assessment based on connection point analysis for transmission system ［J］.Electric Power Automation Equipment，2012，32（3）：76-80.

［7］王浩浩，管霖，吴熳红.配电网可靠性评估中预安排停电的实用模型［J］.电力系统自动化，2011，35（23）：59-63.WANG Haohao，GUAN Lin，WU Manhong.Mathematical model ofscheduled outage in reliability assessmentofdistribution network［J］.Automation of Electric Power Systems，2011，35（23）：59-63.

［8］郭永基.电力系统可靠性分析［M］.北京：清华大学出版社，2003：172-179.

［9］万国成，任震，田翔.配电网可靠性评估的网络等值法模型研究［J］.中国电机工程学报，2003，23（5）：48-52.WAN Guocheng，REN Zhen，TIAN Xiang.Study on model of reliability-network-equivalent of distribution system reliability evalution［J］.Proceedings of the CSEE，2003，23（5）：48-52.

［10］陈璨，吴文传，张伯明，等.基于元件组的复杂配电网可靠性评估［J］.电网技术，2012，36（8）：48-52.CHEN Can，WU Wenchuan，ZHANG Boming，et al.Reliability evaluation for large-scale distribution network based on component groups［J］.Power System Technology，2012，36（8）：48-52.

［11］许丹，唐巍.基于区域可达性分析的复杂配电网可靠性评估［J］.电工技术学报，2011，26（6）：172-177.XU Dan，TANG Wei.Reliability evaluation of complex distribution networks based on regional accessibility analysis［J］.Transactions of China Electrotechnical Society，2011，26（6）：172-177.

［12］何晓群，刘文卿.应用回归分析［M］.北京：中国人民大学出版社，2001：156-158.

［13］杨杰，吴中如.观测数据拟合分析中的多重共线性问题［J］.四川大学学报：工程科学版，2005，37（5）：19-24.YANG Jie，WU Zhongru.Research on the multicollinearity existing inobservation data simulation and analysis［J］.Journal of Sichuan University：Engineering Science Edition，2005，37（5）：19-24.

［14］马雄威.线性回归方程中多重共线性诊断方法及其实证分析［J］.华中农业大学学报：社会科学版，2008（2）：78-85.MA Xiongwei.Diagnosis and empirical analysis on multicollinearity in linear regression model［J］.Journal of Huazhong Agricultural University：Social Sciences Edition，2008（2）：78-85.

［15］陈希孺，王松桂.近代回归分析：原理方法及应用［M］.合肥：安徽教育出版社，1987：4-6，218-223.

［16］牛胜锁，梁志瑞，张建华，等.基于广义岭估计的电力系统谐波状态估计［J］.电力自动化设备，2012，32（7）：94-98.NIU Shengsuo，LIANG Zhirui，ZHANG Jianhua，etal.Power system harmonic state estimation based on generalized ridge estimation［J］.Electric Power Automation Equipment，2012，32（7）：94-98.