气象环境相关的输电线路故障时间分布特征及模拟

王 建 ，熊小伏 ，李 哲 ，梁 允 ，翁世杰

（1.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044；2.国网河南省电力公司电力科学研究院，河南 郑州 450052）

0 引言

电网多年运行经验表明，架空输电线等输变电设备长期暴露于大气环境之中，其能否安全可靠运行与外部气象环境有密切关系。因此，认识输电线路的故障特性、提升电网运行可靠性水平一直是电力系统规划、调度运行、设备维修等工作所关注的重点。

文献［1-2］指出自然灾害、气候因素是造成我国架空线路非计划停运的主要原因，2011年自然灾害、气候因素导致的220～500 kV输电线路非计划停运占非计划停运总次数的84.36%。气象环境影响输电线路的安全可靠运行主要有2种形式：气象条件的累积作用，如温度、日照的逐渐累积和不可逆过程导致导线抗拉强度损失的老化失效；气象灾害的冲击作用，如雷击、台风、山火等对输电线的电气绝缘或物理强度的破坏而导致强迫停运。

在气象环境对输电线路的累积作用研究方面，文献［3-4］考虑了环境温度、风速、风向、日照等气象条件对输电线路老化作用的影响，提出了用威布尔分布来描述计及气象条件累积作用的输电线路老化失效模型；文献［5］在进行输电线路动态增容运行风险评估时，提出模拟产生与线路热容量相关的环境温度、风、日照等气候模型各参数后验分布的随机序列来获取气候模型，进而利用该模型通过蒙特卡洛模拟来预测导线温度的分布。

在气象环境对输电线路的冲击作用研究方面，文献［6］对北京电网1990—2009年间的电网故障记录进行了分类筛选与统计分析，研究了与气象相关的电网故障逐月时间分布特征，但未给出明确的数学描述；文献［7］利用1983—2008年河北省灾情直报数据，分析了大风对河北电网设施损毁的时空分布规律，指出故障逐月分布呈现明显的单峰特性，6—8月为主要的故障高峰期；文献［8］分析了我国南方某地区电网跳闸事件的时间分布特征，指出故障集中发生在4—9月，与当地的雷电天气时间分布（4—9月）、暴雨天气时间分布（5—9月）、台风天气时间分布（4—10月）成明显的同步相关性特征。文献［9］建立了强风雨荷载下输电线路的可靠性模型。前述研究成果揭示了电网故障与气象灾害之间的关联关系，但尚缺乏对这些关联关系的数学描述。

在电网概率风险评估中，描述元件故障前工作时间和故障后修复时间的概率分布［10-14］主要有：指数分布、威布尔分布、伽马分布、正态分布、对数正态分布等。其中，故障前工作时间分布模型主要是线路整个寿命周期内的结构老化模型，对于气象灾害的冲击作用而导致的短期强迫失效不具有适用性。

针对上述问题，本文从气象对电网影响的周期性特征出发，提出故障率依据历年相同月份故障事件统计计算的方法，并在获得各月故障率样本的基础上，寻求全年纵向时间方向的故障率分布函数，由此得到时间相依的故障率数学模型，用以反映不同地区、不同电压等级、不同气象环境下的输电线路故障时间变化的规律。然后采用一次基波傅里叶函数来模拟输电线路故障率的逐月分布情况，并以故障逐月分布具有双峰特性的中部地区和具有平缓单峰特性的南方沿海地区的电网实际故障样本进行拟合检验。进一步，针对单峰特性的故障率逐月分布，使用更少参数的高斯函数和威布尔函数分别进行拟合检验。最后，使用最常用的几种概率分布模拟气象相关的输电线路强迫停运时间的概率分布，并分析和比较了各分布拟合函数的优劣。

1 气象所致输电线故障时间特征分析

国内外许多专家学者在气象条件等环境因素对输电网可靠性的影响方面已开展了一些研究，其目的是更客观地反映电网可靠性水平随气象条件的变化。主要采用的方法包括：分状态考虑气象因素［15-19］，即把气候状态分为两态、三态甚至多态；具体考虑在某一种气象条件下的故障率估算或基于气象预报的故障率预测［20-28］，并据此进行电力系统风险评估。

然而，大部分地区的输电线路均要经历一年四季多种气象环境因素的作用，仅以个别因素或少量状态来描述输电线路的风险水平仍然不够完整，也难以反映一年内不同时期线路风险水平的变化。

如前所述，自然灾害、气候因素是造成架空线路非计划停运的主要原因。文献［29］指出：气候系统的变化特征具有自记忆特征，气候事件序列在不同的时间标度上有相似的统计特性，表现出长程相关性。以天文角度划分四季的方法，适用于我国长江、黄河沿线及其之间的中部地区［30］。这些地区气候特征四季分明，气象灾害也有明显的季节特性，夏季有雷雨、飑线风等强对流天气，冬季有覆冰、舞动、污闪等，春季有少数地区存在大风天气，秋季存在一些山火灾害，总之是冬夏相对较多、春秋相对较少，呈现双峰特性。这些地区的输电线受气象灾害冲击影响，线路强迫停运也普遍存在冬夏多、春秋少的双峰特性。

对于我国南方沿海地处较低纬度的南亚热带季风气候区域，四季划分方法采用的是气候学标准。例如，南方沿海某地区的气候特征［31］如表1所示。

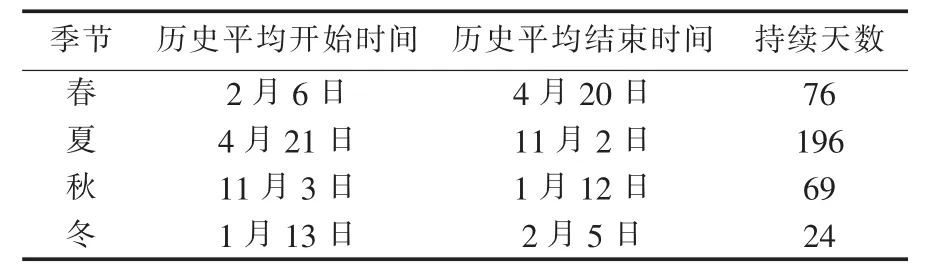
表1 南方沿海某地区四季划分表Table1 Partition of four seasons for a coastal area in southern China

南方沿海地区气候特征呈现明显的长夏短冬特点，输电线路主要受长夏季中的雷电、台风、大风、暴雨影响，而冬季很短且无冰雪，导线不受覆冰和舞动影响，故障时间分布呈平缓单峰特性。

2 历史同期月故障率统计方法

由于气象灾害年际爆发有差异，与气象环境相关的线路故障率在不同年份也有差异。尽管年度间有差异，但多年中历史同期的月份气象灾害导致的线路故障分布却基本不变。

根据故障率的定义：

则可按式（2）求取历史同期各月故障率：

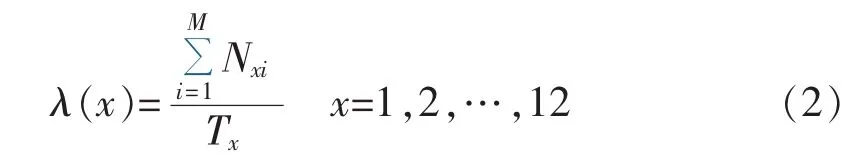
其中，λ（x）为历史同期第 x 月的故障率（次/月）；Nxi为第i年第x月中的故障次数；Tx为第x个月的时间；M为统计年数。

例如，根据式（2）对我国中部某省电网多年数据进行统计分析，如图1所示，其发生故障的峰值月份出现在1月和7月，谷值出现在5月和10月，故障的时间分布具有明显的“峰-谷-峰-谷”特性。进一步结合当地的气候特点分析，该电网故障主要受冬季覆冰、舞动、污闪，夏季强对流天气导致的雷击、风害影响，在春秋季节有一些鸟害和山火。其中输电线冰害主要出现在每年的1—3月，舞动跳闸事故主要发生在每年的1月、2月和11月，雷击跳闸事故集中出现在每年的6—8月，鸟害发生的时间相对集中在3、4月的鸟儿筑巢期及11月候鸟迁徙季节，大风或风偏灾害主要发生在4—6月。因此，采用按多年历史同期各月故障率为依据而不是以年均故障率为参考的时变故障率，更能反映输电线路的时间相依故障规律。

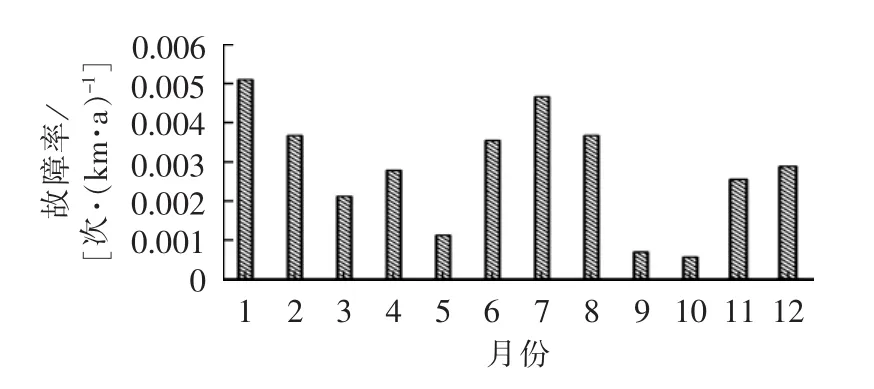
图1 某省电网逐月故障率柱状图Fig.1 Bar chart of monthly failure rate for a provincial power grid

使用各月故障率的有名值来描述时间分布规律特征时，可能因为不同地域电网的差异，虽然分布曲线形状相似，但参数值变化很大。因此，本文使用规范化的故障率函数来反映故障率的逐月时间分布特征，故障率规范化值计算公式为：

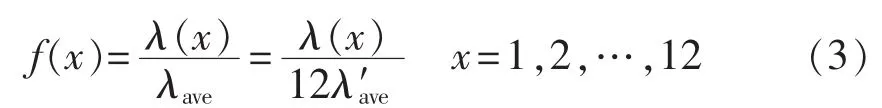
其中，λ（x）为历史同期第 x 月的故障率（次/月）；λave为多年平均值故障率（次 /a）；λ′ave为归算到月的多年平均值故障率（次/月）；f（x）为历史同期各月故障率规范化值分布函数。

3 故障率逐月分布特征模拟

3.1 故障率逐月分布函数假设

如前所述，输电线路故障率是随时间变化的，且不同地区由于其地理位置和输电网络布局的差异，也具有不同的故障率时间分布特性。因此，在得到历史同期各月故障率基础上，若能模拟得到全年故障率的时间变化特性，则可以用于电网运行与检修策略的制定。

我国长江沿线到黄河沿线之间的中部地区具有春夏秋冬四季分明的气候特点，输电线故障逐月时间分布通常具有“峰-谷-峰-谷”特性，由于可以通过调节周期系数来改变峰谷周期，调节均值系数、幅值系数来改变峰谷值，傅里叶函数对多峰周期性曲线的拟合具有很好的适应性。因此，可假设其输电线的故障时间分布为一次基波傅里叶函数。一次基波傅里叶函数的表达式如下：

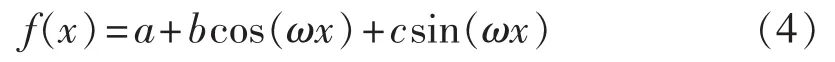
其中，a、b、c、ω 为拟合待定系数；x为月份。

南方沿海地区具有长夏短冬的气候特点，输电线故障具有明显的平缓单峰月分布特征，使用一次基波傅里叶函数需要拟合4个参数。而高斯函数和威布尔函数分别只需3个和2个参数就能较好模拟平缓单峰曲线［32］，因此进一步假设这类地区输电线故障的逐月时间分布为高斯函数或威布尔函数。

高斯函数的表达式如下：

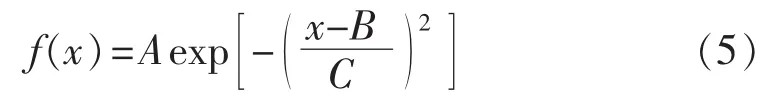
其中，A、B、C为拟合待定系数。

威布尔函数的表达式如下：

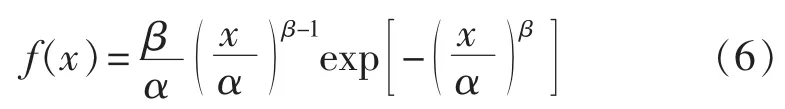
其中，α为待定尺度参数；β为待定形状参数。

3.2 一次基波傅里叶函数参数拟合

以我国中部某省电网2001—2011年间与气象环境相关的236次220 kV线路故障事件为样本，采用上述傅里叶函数表示的故障率逐月分布假设，进行函数拟合。拟合结果如图2所示，图中故障率规范化值为标幺值，后同。各系数拟合值为：a=0.0820，b=0.0142，c=0.0476，ω=1.0790。拟合优度：判定系数Rsquare=0.7123，均方根误差δRMSE=0.0275。

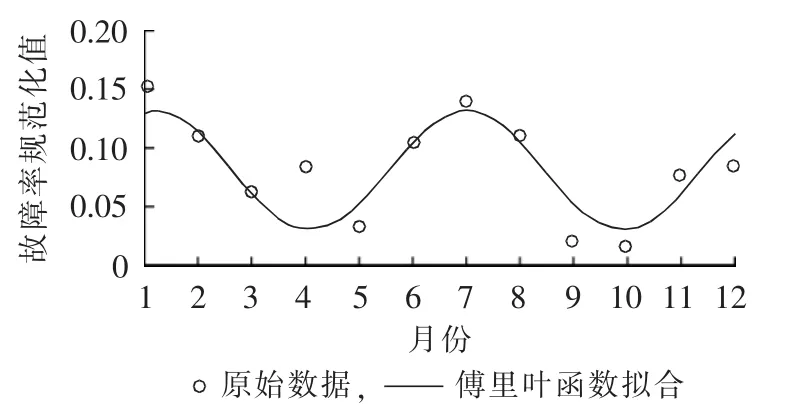
图2 中部某省220 kV线路故障率逐月分布傅里叶函数拟合曲线Fig.2 Monthly distribution curve of 220 kV transmission line failure rate fitted by Fourier function for a province of central China

对于故障率逐月时间分布呈平缓单峰特性的地区，本文以南方某沿海电网的2007—2013年间与气象环境相关的162次220 kV线路故障事件为样本，进行了函数拟合，拟合结果如图3所示，各系数拟合值为：a=0.1020，b=-0.0057，c=-0.1054，ω=0.6619。拟合优度为：判定系数Rsquare=0.857 8，均方根误差δRMSE=0.0379。

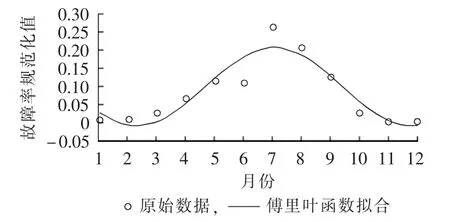
图3 南方某地220 kV线路故障率逐月分布傅里叶函数拟合曲线Fig.3 Monthly distribution curve of 220 kV transmission line failure rate fitted by Fourier function for a city in southern China

从上面两例可以看出，通过改变均值系数a，幅值系数b、c，和周期系数ω，傅里叶函数能够适应峰谷交替和单峰特性的故障率逐月分布曲线拟合，方便实用，可推广性强。

3.3 单峰曲线的多种函数参数拟合

对于分别只需3个和2个参数就能较好模拟平缓单峰曲线的高斯函数和威布尔函数，仍然以南方某沿海电网的2007—2013年间与气象环境相关的162次220 kV线路故障事件为样本，进行了对比函数拟合，结果如表2和图4所示。可见，对于平缓单峰特性的南方沿海地区，可以使用表达式更为复杂但参数更少的高斯函数和威布尔函数进行模拟。

表2 南方某地220 kV线路故障率逐月分布拟合结果Table 2 Results of monthly failure rate distribution fitting for 220 kV transmission line of a city in southern China

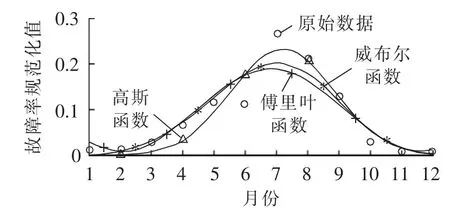
图4 南方某地220 kV线路故障率逐月分布拟合曲线Fig.4 Monthly distribution curve of 220 kV transmission line failure rate fitted for a city in southern China

更进一步，对于其他电压等级的线路，本文提出的故障率逐月分布函数假设是否同样适用？为此以南方某沿海电网2007—2013年间与气象环境相关的569次110 kV线路故障事件为样本，进行了对比拟合检验，结果如表3和图5所示。

表3 南方某地110 kV线路故障率逐月分布拟合结果Table 3 Results of monthly failure rate distribution fitting for 110 kV transmission line of a city in southern China

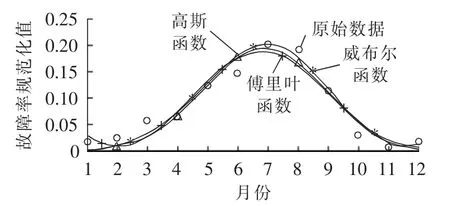
图5 南方某地110 kV线路故障率逐月分布拟合曲线Fig.5 Monthly distribution curve of 110 kV transmission line failure rate fitted for a city in southern China

对比图4和图5以及表2和表3可以得出以下结论。

a.南方沿海地区电网不同电压等级的输电线路，其故障率逐月分布呈现明显相似的单峰特性，单峰峰值均出现在7月，模拟结果参数相近；同时，由于110 kV线路的故障样本数更多，拟合结果更好。

b.使用傅里叶函数、威布尔函数、高斯函数均能很好地模拟这种单峰特性的故障率逐月分布曲线，威布尔函数虽然表达式复杂，但只需通过改变形状参数和尺度参数，就可以达到更好的拟合优度。

因此，在实际运用中可以根据模拟的准确度需要，选择表达式简单的4参数一次基波傅里叶函数，或者表达式复杂的2参数威布尔函数。

4 输电线路强迫停运时间分布特征模拟

前文分析和模拟了输电线路故障率逐月分布函数，而对于输电线路强迫停运时间，描述其概率密度函数分布的主要有：指数分布、威布尔分布、伽马分布、对数正态分布等。此外，文献［13］使用埃尔朗分布来描述维修时间的概率分布，而埃尔朗分布实质上是一种形状参数为整数的伽马分布。文献［33］提出了使用时域齐次马尔科夫过程描述停运模型的“叠加指数分布”，相当于2参数的指数分布。

指数分布的表达式如下：

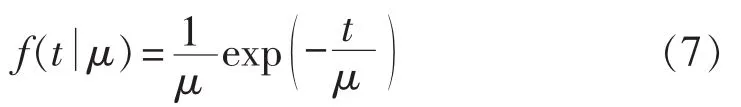
其中，t为停运时间；μ为均值，方差为μ2。

威布尔分布的表达式如下：

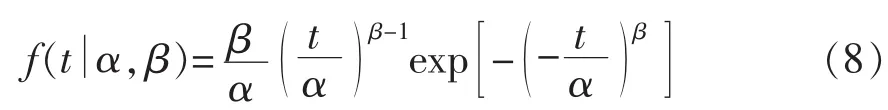
其中，α为尺度参数；β为形状参数。

伽马分布的表达式如下：

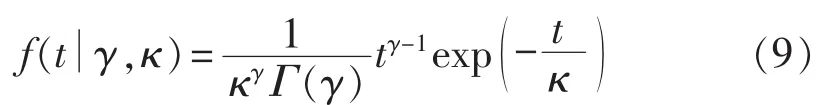
其中，γ为形状参数；κ为尺度参数；Γ（·）为伽马函数，如式（10）所示。

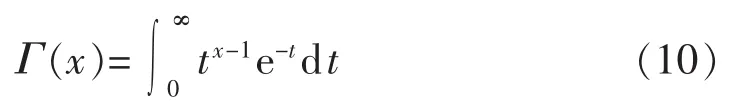
对数正态分布的表达式如下：

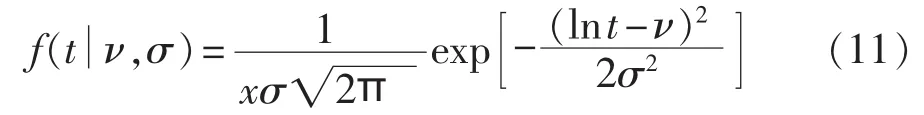
其中，ν为对数均值；σ为对数标准差。

对于以上几种常用停运时间概率密度函数，受气象灾害影响而导致强迫停运的输电线路，其停运时间分布使用哪种更为合适？为此本文以南方沿海某地区电网2007—2013年间110～220 kV电网由于气象相关原因造成的134次输电线强迫停运事件为样本，对停运时间概率密度函数进行分布拟合检验。

样本停运时间序列的统计均值为8.1207 h，方差为51.6451。分布拟合采用极大似然估计法，拟合检验采用0.01显著性水平的χ2检验法，分布拟合和检验结果如图6和表4所示。

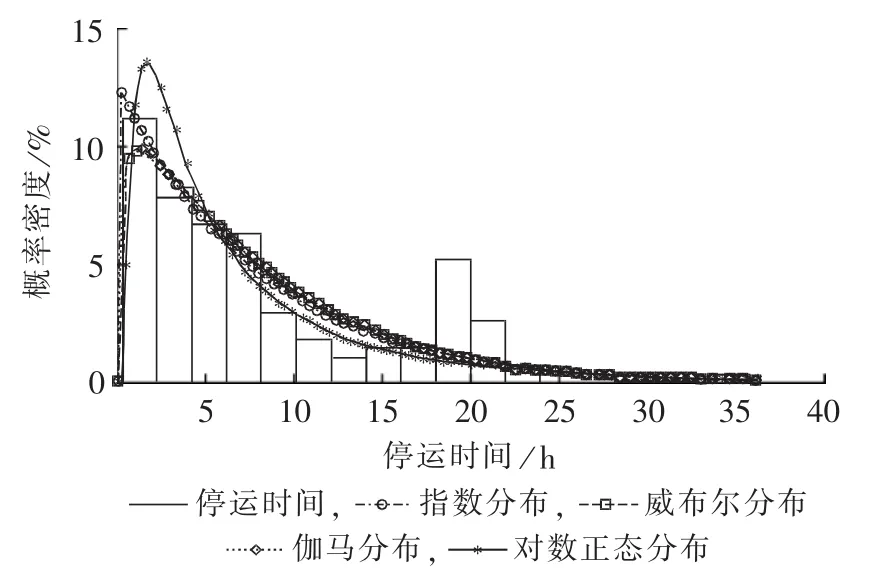
图6 4种概率密度函数描述效果比较Fig.6 Comparison of representing effect among four probability density functions

表4中lnL表示对数极大似然估计值，Emean表示拟合函数的均值，δvar表示拟合函数的方差。从表4可见：对数正态分布拟合的均值9.301 8和方差221.9330均与样本均值8.1208和样本方差51.6451差别较大，虽然在样本较多的情况检验通过，但其参数估计值却最差（lnL值最小）。由于威布尔分布和伽马分布可以通过调节形状参数或尺度参数来反映概率密度曲线的变化，因此使用威布尔分布或伽马分布均能较好地拟合停运时间的概率密度函数。同时，指数分布由于只有一个均值参数μ，当样本方差接近μ2时，亦可很好地模拟停运时间的概率密度函数，但样本方差同指数模拟的方差μ2差别较大时，拟合优度就较差。

本文样本参数的统计均值8.1207 h，与文献［1-2］公布的2010、2011年全国220 kV线路因气象环境相关的平均停运时间分别为8.0452、13.2107 h是吻合的。由于指数分布只需估计参数的均值，因此在缺乏大量详细样本信息时，可以通过查阅各地报往电力可靠性管理中心的数据，使用指数分布描述停运时间概率分布。

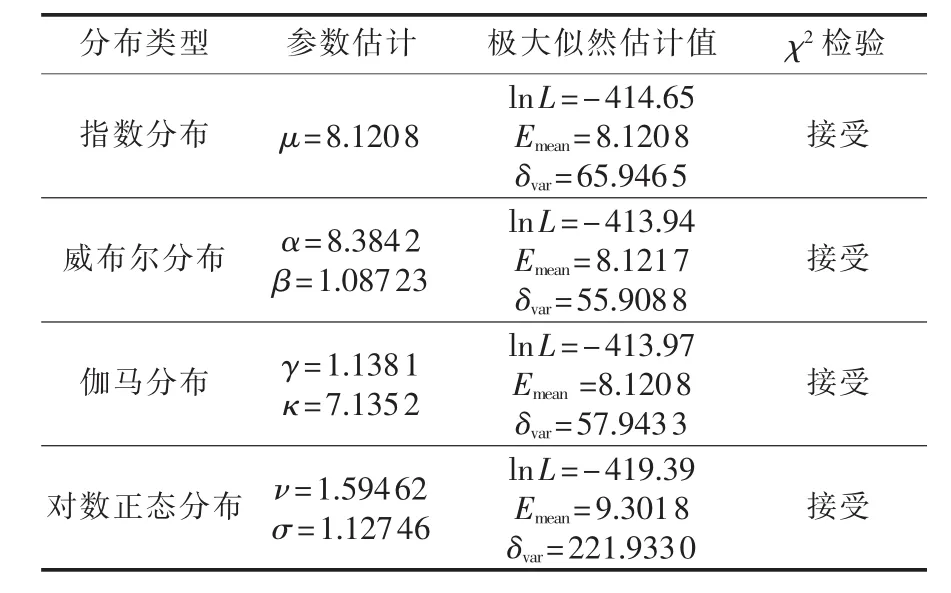
表4 4种概率密度函数拟合结果Table 4 Fitting results of four probability density functions

5 结论

针对气象环境相关的输电线故障率逐月时间分布特征和强迫停运时间概率分布特征的数学描述问题，本文提出了以月为时间尺度的时变故障率计算方法，用于反映输变线路的时间相依的故障规律。在此基础上给出了输电线故障率逐月分布函数强迫停运时间函数模拟方法，并以故障逐月分布具有双峰特性的中部地区和具有平缓单峰特性的南方沿海地区电网的实际故障样本进行了拟合验证。通过研究得出如下结论。

a.输电线路时间相依的故障规律，可通过拟合历史同期各月故障率的时间分布，得到故障率逐月分布函数来模拟，并可用于预测输电线路在未来时段的故障率。

b.可以采用一次基波傅里叶函数模拟具有峰谷交替特性的故障率逐月时间分布函数；对于单峰特性的故障率逐月分布曲线，使用傅里叶函数、威布尔函数、高斯函数均能很好地模拟，在实际运用中可以根据模拟的准确度需要，选择繁简程度不同的函数。

c.在描述输电线强迫停运时间分布时，指数分布因只有1个均值参数，模拟的分布函数方差常常不满足样本方差，而威布尔分布和伽马分布可以通过调节形状参数或尺度参数来反映概率密度曲线的变化，因此能更好地模拟停运时间的概率密度函数。

［1］陈丽娟，李霞.2011年全国输变电设施可靠性分析［J］.中国电力，2012，45（7）：89-93.CHEN Lijuan，LI Xia.Statistic analysis on reliability of power transmission and transformation facilities in China in 2011 ［J］.Electric Power，2012，45（7）：89-93.

［2］陈丽娟，胡小正.2010年全国输变电设施可靠性分析［J］.中国电力，2011，44（6）：71-77.CHEN Lijuan，HU Xiaozheng.Statistic analysis on reliability of powertransmission and transformation facilitiesin China in 2010［J］.Electric Power，2011，44（6）：71-77.

［3］何剑，程林，孙元章，等.条件相依的输变电设备短期可靠性模型［J］. 中国电机工程学报，2009，29（7）：39-46.HE Jian，CHENG Lin，SUN Yuanzhang，et al.Condition dependent short-term reliability models of transmission equipment［J］.Proceedings of the CSEE，2009，29（7）：39-46.

［4］孙元章，程林，何剑.电力系统运行可靠性理论［M］.北京：清华大学出版社，2012：72-74.

［5］王孔森，盛戈皞，王葵，等.输电线路动态增容运行风险评估［J］.电力系统自动化，2011，35（23）：11-15，21.WANG Kongsen，SHENG Gehao，WANG Kui，etal.Operation risk assessment of a transmission line dynamic line rating system［J］.Automation of Electric Power Systems，2011，35（23）：11-15，21.

［6］段大鹏，张玉佳，郭鑫宇，等.气象因素对北京电网设备影响的统计规律及时空分布特征［J］. 高压电器，2013，49（7）：75-79.DUAN Dapeng，ZHANG Yujia，GUO Xinyu，et al.Statistical law and distribution characteristic ofthe impacts of climate on equipment of Beijing power network［J］.High Voltage Apparatus，2013，49（7）：75-79.

［7］付桂琴，曹欣.雷雨大风与河北电网灾害特征分析［J］.气象，2012，38（3）：353-357.FU Guiqin，CAO Xin.The characteristic analysis of thunderstorm gale and electrical network disaster in Hebei［J］.Meteorological Monthly，2012，38（3）：353-357.

［8］方丽华，熊小伏，方嵩，等.基于电网故障与气象因果关联分析的系统风险控制决策［J］. 电力系统保护与控制，2014，42（17）：113-119.FANG Lihua，XIONG Xiaofu，FANG Song，et al.Power system risk control decision based on cause and effect correlation analysis of fault and meteorology［J］.Power System Protection and Control，2014，42（17）：113-119.

［9］杨清，魏亚楠，赵渊，等.强风雨荷载冲击下的输电线路可靠性建模方法［J］. 电力自动化设备，2015，35（2）：133-137.YANG Qing，WEI Yanan，ZHAO Yuan，et al.Reliability model of transmission lines under impact of strong wind and rain［J］.Electric Power Automation Equipment，2015，35（2）：133-137.

［10］赵渊，郭胤，谢开贵.考虑参数不确定的电网可靠性概率分布特征［J］. 电网技术，2013，37（8）：2165-2172.ZHAO Yuan，GUO Yin，XIE Kaigui.Research on probability distribution characteristics ofbulk powersystem reliability considering parameter uncertainty［J］.Power System Technology，2013，37（8）：2165-2172.

［11］LI Wenyuan.Risk assessment of power systems：models，methods，and applications［M］.Hoboken，New Jersey，USA：Wiley-IEEE Press，2004：43-68.

［12］KIM J S，KIM T Y，SUN H.An algorithm for repairable item inventory system with depot spares and general repair time distribution［J］.Applied Mathematical Modeling，2007，31（5）：795-804.

［13］金星，洪延姬，沈怀荣，等.工程系统可靠性数值分析方法［M］.北京：国防工业出版社，2002：6-11.

［14］ZHANG Dabo，LI Wenyuan，XIONG Xiaofu.Overhead line preventivemaintenancestrategybased on condition monitoring and system reliabilityassessment［J］.IEEE Transactions on Power Systems，2014，29（4）：1839-1846.

［15］BILLINTON R，CHENG L.Incorporation of weather effects in transmission system models for composite system adequacy evaluation［J］.IEE Proceedings Generation，Transmission and Distribution，1986，133（6）：319-327.

［16］BHUIYAN M R，ALLAN R N.Inclusion of weather effects in composite system reliability evaluation using sequential simulation［J］.IEE Proceedings Generation，Transmission and Distribution，1994，141（6）：575-584.

［17］陈永进，任震，黄雯莹.考虑天气变化的可靠性评估模型与分析［J］. 电力系统自动化，2004，28（21）：17-21.CHEN Yongjin，REN Zhen，HUANG Wenying.Model and analysis of power system reliability evaluation considering weather change［J］.Automation of Electric Power Systems，2004，28（21）：17-21.

［18］LIU Yong，SINGH C.A methodology for evaluation of hurricane impact on composite power system reliability［J］.IEEE Transactions on Power Systems，2011，26（1）：145-152.

［19］刘洋，周家启.计及气候因素的大电力系统可靠性评估［J］.电力自动化设备，2003，23（9）：60-62.LIU Yang，ZHOU Jiaqi.Incorporating weather effect in bulk power system reliability evaluation［J］.Electric Power Automation Equipment，2003，23（9）：60-62.

［20］朱清清，严正，贾燕冰，等.输电线路运行可靠性预测［J］.电力系统自动化，2010，34（24）：18-22.ZHU Qingqing，YAN Zheng，JIA Yanbing，et al.Prediction of transmission operating reliability［J］.Automation of Electric Power Systems，2010，34（24）：18-22.

［21］朱益华，罗毅，段涛，等.基于输电线路实时评估模型的电力系统静态安全在线风险评估［J］. 电力自动化设备，2014，34（7）：150-156.ZHU Yihua，LUO Yi，DUAN Tao，et al.Online risk assessment based on real-time evaluation model of transmission line for static security of power system［J］.Electric Power Automation Equipment，2014，34（7）：150-156.

［22］孙羽，王秀丽，王建学，等.架空线路冰风荷载风险建模及模糊预测［J］. 中国电机工程学报，2011，31（7）：21-28.SUN Yu，WANG Xiuli，WANG Jianxue，et al.Wind and ice loading risk model and fuzzy forecast for overhead transmission lines［J］.Proceedings of the CSEE，2011，31（7）：21-28.

［23］谢云云，薛禹胜，文福拴，等.冰灾对输电线故障率影响的时空评估［J］. 电力系统自动化，2013，37（18）：32-41，98.XIE Yunyun，XUE Yusheng，WEN Fushuan，et al.Space-time evaluation for impact of ice disaster on transmission line fault probability［J］.Automation of Electric Power Systems，2013，37（18）：32-41，98.

［24］宋嘉婧，郭创新，张金江，等.山火条件下的架空输电线路停运概率模型［J］. 电网技术，2013，37（1）：100-105.SONG Jiajing，GUO Chuangxin，ZHANG Jinjiang，et al.A probabilistic model of overhead transmission line out-age due to forest fire［J］.Power System Technology，2013，37（1）：100-105.

［25］包博，程韧俐，熊小伏，等.一种计及微地形修正的输电线台风风险预警方法［J］. 电力系统保护与控制，2014，42（14）：79-86.BAO Bo，CHENG Renli，XIONG Xiaofu，et al.A typhoon risk early warning method for power transmission line considering micro-terrain correction［J］.Power System Protection and Control，2014，42（14）：79-86.

［26］XIONG Xiaofu，WENG Shijie，WANG Jian.An online early warning method for wind swing discharge of conductor towards tangent tower and jumper towards strain tower［J］.IEEE Transactions on Power Delivery，2015，30（1）：114-121.

［27］李哲，梁允，熊小伏，等.基于层次分析法的输电线塔基降雨滑坡预警方法［J］. 智能电网，2014，2（9）：29-33.LI Zhe，LIANG Yun，XIONG Xiaofu，et al.A rainfall caused landslide early-warning method fortransmission line tower based on analytic hierarchy process［J］.Smart Grid，2014，2（9）：29-33.

［28］熊小伏，翁世杰，王建，等.电网台风风险预警系统方案设计［J］.重庆大学学报，2014，37（7）：27-32.XIONG Xiaofu，WENG Shijie，WANG Jian，et al.Research and application of typhoon risk early warning system for power grid［J］.Journal of Chongqing University，2014，37（7）：27-32.

［29］封国林，侯威，支蓉，等.极端气候事件的检测、诊断与可预测性研究［M］. 北京：科学出版社，2012：234-241.

［30］丁一汇. 中国气候［M］. 北京：科学出版社，2013：392.

［31］深圳市气象局. 深圳市气候概况［EB/OL］. ［2015-03-07］.http：∥www.szmb.gov.cn/article/QiHouYeWu/qihouxinxigongxiang /GaiKuangSiJiTeZheng/2013.

［32］杨振海，程维虎，张军舰.拟合优度检验［M］.北京：科学出版社，2011：14-36.

［33］宁辽逸，吴文传，张伯明.一种适用于运行风险评估的元件修复时间概率分布［J］. 中国电机工程学报，2009，29（16）：15-20.NING Liaoyi，WU Wenchuan，ZHANG Boming.A novel probability distribution of component repair time for operation risk assessment［J］.Proceedings of the CSEE，2009，29（16）：15-20.