基于无迹变换含分布式电源系统的随机潮流

代景龙，韦 化，鲍海波，白晓清

（广西大学 广西电力系统最优化与节能技术重点实验室，广西 南宁 530004）

0 引言

电力系统中存在各种随机因素，如发电机组和输电网络元件的随机故障停运、负荷的波动等，尤其是随着分布式电源的大规模并网，给电力系统的规划和运行带来了前所未有的不确定因素。确定性潮流忽略了系统模型中节点负荷功率、分布式电源出力的不确定性，只能反映系统在某种确定条件下的稳态运行状况。随机潮流［1-4］SPF（Stochastic Power Flow）利用概率统计方法处理系统中随机变化的因素，比传统的确定性潮流计算更能全面地捕捉系统的运行特性，便于对系统中的潜在危险及薄弱环节进行量化分析。

随机潮流自Borkowska于1974年提出［1］至今，其求解方法主要有点估计法PEM（Point Estimation Method）［5-7］、蒙特卡洛模拟 MCS（Monte Carlo Simulation）法［8-10］和解析法［11-13］。PEM 根据已知随机变量的概率分布，近似求取待求随机变量的概率分布，计算效率较高，但输出结果的高阶矩误差较大［14-15］。MCS方法需要大量的随机采样以保证其计算精度，求解速度较慢，制约了其实际的工程应用。解析法利用线性化的思想求解非线性模型，但线性化过程需要输入和输出变量的线性关系，将降低其计算精度，计算量随着系统规模的增大迅速增长。

无迹变换 UT（Unscented Transformation）［16-18］通过一系列确定性选择的Sigma点，近似非线性地映射随机变量的概率密度分布。其处理随机潮流问题具有速度快、精度不低于二阶、易于处理随机变量的相关性、无需对非线性函数进行近似，且受输入随机变量分布类型的限制较小等优点［19］。

UT方法包括确定性采样和非线性变换两部分，其核心是选择合适的采样策略，换言之，确定合适的Sigma点数量、位置以及相应的权重，保证较高计算效率的同时，使所抽取的Sigma点能够更为全面地捕捉输入随机变量的均值和标准差信息［20］。UT采样策略有对称采样、最小偏度单形采样、超球体单形采样。文献［19］和［21］分别把UT应用于概率最优潮流和随机潮流的计算，不仅大幅提高了计算效率，而且克服了线性化方法需要计算非线性函数雅可比矩阵的缺点，但均未对UT方法不同采样策略的计算效率和数值稳定性等进行比较。

本文提出了基于UT的随机潮流计算方法，比较了UT方法的3种采样策略处理含分布式电源系统随机潮流问题的精度、效率和适用条件，引入比例及高阶信息参数以减小局部效应及高阶项误差，并考虑随机变量的相关性对输出随机变量概率分布的影响。IEEE30、IEEE118和IEEE300节点标准系统计算结果表明：3种采样策略的UT方法在计算规模、求解精度、稳定性和实时性等方面各具优势，实际应用中，可根据随机变量的数目以及系统对特定条件的要求，综合选择适当的采样策略；其中，对称采样策略的UT方法数值稳定性较高，更适用于大规模电力系统随机潮流的计算。

1 随机潮流计算模型

考虑分布式电源出力的随机性，负荷的不可预测性，随机潮流计算模型可描述为［20］：

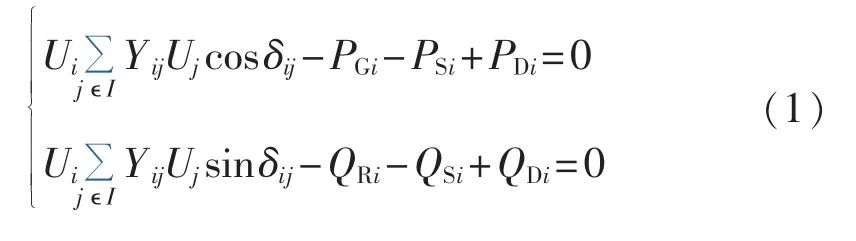
其中，i，jϵSB，SB为节点集合；I为与节点 i所联接支路的对应节点集合；PGi、QRi和 PDi、QDi分别为节点 i的有功功率、无功功率和有功负荷、无功负荷；PSi、QSi分别为节点i所接入分布式电源的有功和无功功率；Ui、δi分别为节点 i的电压幅值和相角；Yij为节点导纳矩阵i行j列元素的幅值，αij为对应的相角，δij=δi-δj-αij。

随机潮流计算模型考虑风电场出力、光伏发电系统出力以及节点负荷功率的随机特性。输入随机变量包括风电场风速v、光伏发电系统的辐照强度r及负荷功率，输出随机变量包括状态输出随机变量（电压幅值和相角）以及支路功率等。

2 系统随机模型

2.1 风力发电系统随机模型

风力发电机组的输出功率随着风速的变化而波动，可以认为风速近似服从双参数威布尔分布，其概率密度函数为：

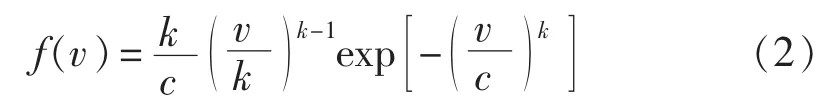
其中，v为风速；k和c分别为威布尔分布的形状参数和尺度参数。

按照式（2）对接入风电机组节点的风速进行抽样，风速样本经过式（3）计算得到节点i风力发电机组的输出功率。节点i所接入风力发电机组的输出功率与风速之间的关系可由分段函数描述为［22］：

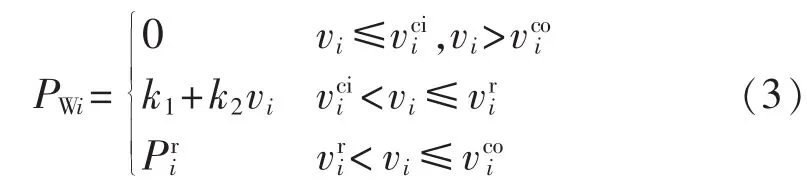
其中为节点i风电机组的切入风速；为节点风电机组的额定风速；为节点i风电机组的切出风速；为节点i风电机组的额定输出功率；k1=和为常数；PWi为节点i风电机组的实际输出功率。

假定接入节点i的NWi台风电机组参数相同且恒功率因数运行，则其输出的有功和无功功率输出可描述为：

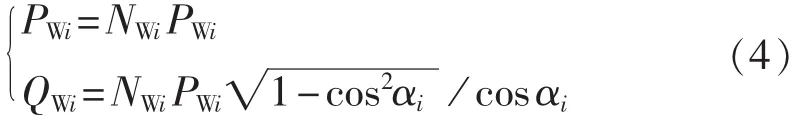
其中，cosαi为节点i风电场的功率因数。

2.2 光伏发电系统随机模型

光伏发电系统的输出功率取决于光照强度以及太阳能电池方阵相对光照的角度，光照强度与气象因素、环境状况有关，又随着季节、时刻的变化而波动。可以认为一个地区的光照强度近似服从Beta分布［23］，其概率密度函数为：

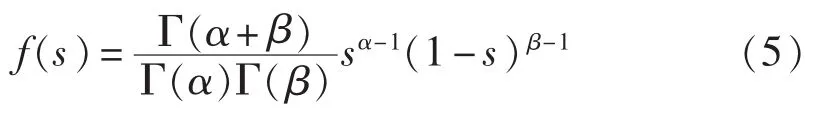
其中，s=r/rmax，r和rmax分别为实际辐照度和最大辐照度（W /m2）；α、β为 Beta分布的 2 个形状参数；Γ 为Gamma函数。

按照式（5）对接入光伏发电系统节点的阳光辐照度抽样，可求得节点i所接入光伏发电系统的输出功率：

其中，ri、Ai和 ηi分别为节点 i光伏阵列辐照度、总面积、总体的光电转换效率。

假设光伏发电系统的功率因数为一常数，节点i光伏发电系统的无功功率输出可表示为：

其中，cosθi为节点i太阳能电池方阵的功率因数。

2.3 负荷随机模型

负荷是电力系统运行中起着决定性作用的不确定因素，其随着时间、季节、天气以及电价的变化而波动，可以近似认为负荷功率是服从正态分布的随机变量。节点i负荷有功功率PDi的概率密度函 数［24］为 ：

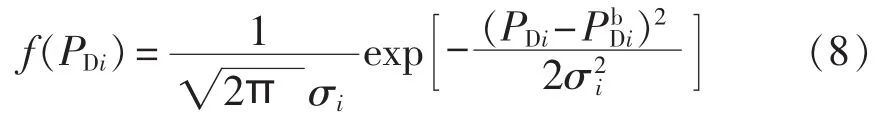
其中，σi为节点i负荷功率的标准差，取为5%；为基态节点负荷功率。

假设负荷功率因数不变，节点i负荷无功功率QDi为：

其中，为基态节点负荷功率。

3 UT

3.1 UT的基本原理

UT通过非线性变换传递均值和协方差信息，其近似非线性函数的概率密度分布，而不是对非线性函数进行近似，不仅更易实现，而且非线性分布统计量的计算精度至少可达到二阶。按照选定的采样策略，确定性地选取一组Sigma点集表征一个概率分布的特征，其均值和协方差矩阵分别为ux和Pxx。对每个Sigma点进行非线性变换y=fUT（x）以传递参数信息，变换后的点集经过加权处理，得到输出随机变量的均值uy和协方差Pyy。其中，x为n维输入随机变量，ux为n维列向量，Pxx为n阶方阵。

UT方法的基本步骤如下。

（1）根据各随机变量的标准差δi以及变量之间的相关性系数ρij，构造协方差矩阵Pxx：

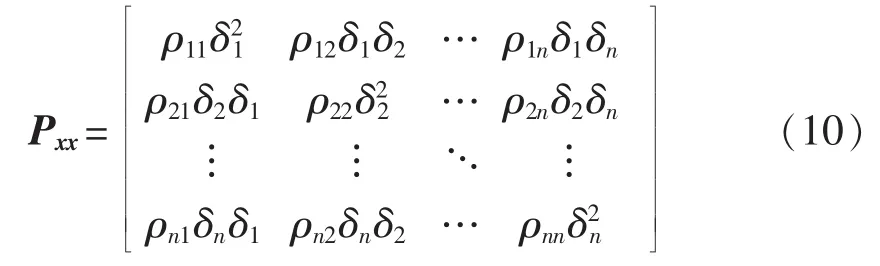
其中，ρij为第i和第j个随机变量之间的相关系数。

（2）以统计量ux和Pxx为基础，选择适当的采样策略构造输入随机变量的Sigma样本点和权重集合，N 为采样点个数，χi和Wi满足：

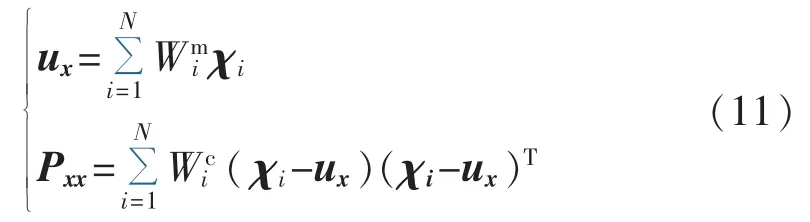
其中，χi为 Sigma 样本点；Wi为对应权重，为均值权重，为协方差权重，可为任意值，但为保证无偏性，需满足式（12）。

（3）对确定性选择的 Sigma 点集｛χi｝进行非线性变换fUT（·），具体见下文不同采样策略的非线性变换过程，得到变换后点集｛yi｝：

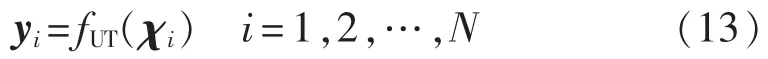
（4）对变换后的点集｛yi｝进行加权处理，即可得到输出随机变量y的均值μy和协方差矩阵Pyy，即：

Sigma点经过标准的向量和矩阵运算，以泰勒展开二阶精度逼近后验的均值和协方差，而无需进行近似线性化和计算非线性变换的导数。与MCS的随机抽样不同，UT的样本点是确定性选取的，即使只抽取了少量Sigma点，但其求得输出随机变量y的均值误差只存在于三阶以上的各项中，方差可达到二阶精度，且可以通过调节参数来改善精度［25］。

UT计算的均值和协方差精度主要取决于Sigma点采样策略，以捕捉状态的概率分布信息，选取的Sigma点越能匹配先验状态的各阶矩统计量，均值和协方差的计算精度就越高。高阶采样策略的UT对称地选取2n2+1个Sigma点，以匹配n维随机向量的前四阶矩及高阶奇次阶矩，但当系统规模较大时，会大幅降低求解的效率。故本文主要比较和分析对称采样、最小偏度单形采样、超球体单形采样3种策略的UT方法处理含分布式电源系统的随机潮流问题，且采样时应用比例及高阶修正以提高计算精度。

3.2 对称采样策略

对称采样策略抽取N=2n+1个相对均值ux对称分布的Sigma采样点捕捉输入随机变量x的概率密度分布。采样点到中心点ux的距离随着输入随机变量维数n的增加而增加，将产生采样点的非局部效应，从而使高阶项的误差增大。本文引入比例及高阶信息参数以减小局部效应及高阶项误差，N个比例对称采样的Sigma点为：

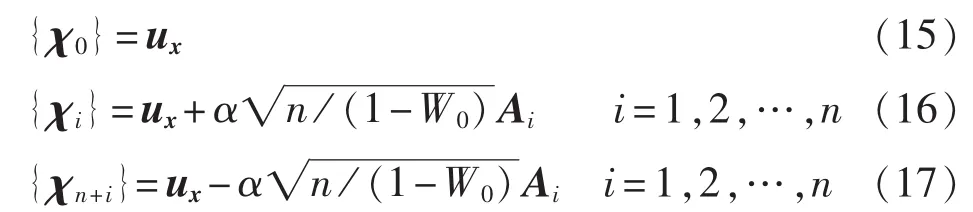
其中，α 为比例缩放参数，取值范围［10-4，1］，可通过调整其取值来改变样本点与ux的距离；A可由Pxx=AAT求得，即，Pxx为正定矩阵，本文平方根矩阵A为通过对Pxx进行Cholesky分解求得，以避免Sigma点中出现复数；Ai为A的第i列元素；各样本点｛χi｝（i＝1，2，…，N）为 n 维列向量。

选择0≤W0≤1，各Sigma采样点所对应均值和协方差的权重分别为：

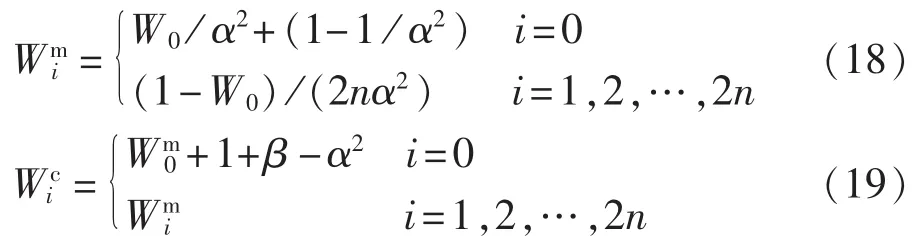
其中，β为高阶信息参数；如果不引入比例及高阶信息参数，则有

3.3 最小偏度单形采样策略

最小偏度单形采样策略抽取N=n+2个样本，其采样规模约为对称采样策略的一半。当样本点对称分布时平均误差最小，偏度值越大倾斜越严重，最小偏度单形采样策略的样本点能在匹配输入随机变量的前两阶矩信息的前提下，使三阶矩（偏度）最小［26］。最小偏度单形采样的基本步骤如下。

（1）选择 0≤W0≤1，各采样点所对应的权值Wi为：

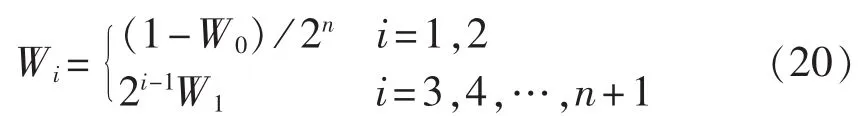
（2）初始化Sigma样本点第一行状态序列：

（3）对于 j＝2，3，…，n 进行递推得到：

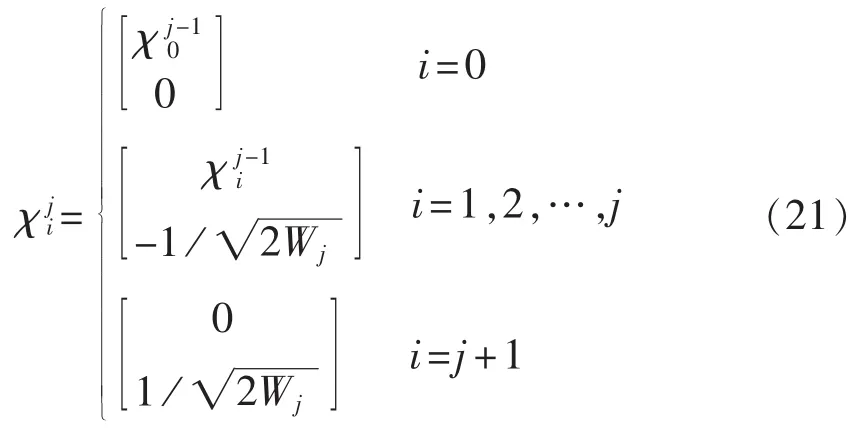
（4）引入比例及高阶信息参数，最小偏度单形采样Sigma样本点与其均值权重、协方差的权重分别为：

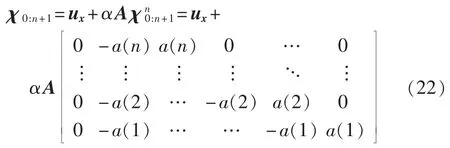
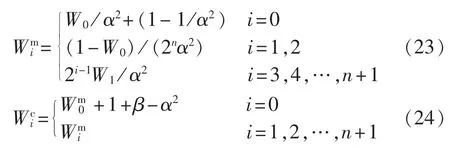
其中，随着输入随机变量维数n的增加，各Sigma点的数值呈现根指数式增长，第n+1维的最大Sigma点数值是第n维的倍。则对于高维系统，将存在部分Sigma点数值巨大，出现潮流收敛困难、量化误差增大等数值问题。虽然本文Sigma样本矩阵均为按列扩展，但对于最小偏度单形采样策略的样本矩阵，其扩展是指数式的，这也是其处理较多随机变量系统时的最大弊病。所以若分布式电源接入数目较多，即增加的输入随机变量的个数较多时，对最小偏度单形采样策略的UT方法影响将较为突出。

3.4 超球体单形采样策略

超球体单形采样［27］抽取N=n+2个样本点匹配前两阶矩，与最小偏度单形采样的采样规模相同。超球体单形采样的基本步骤如下。

（1）选择 0≤W0≤1，各采样点所对应的权值Wi为：

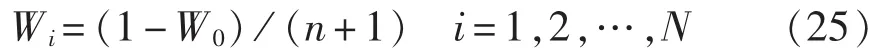
（2）初始化Sigma样本点第一行状态序列

（3）对于 j＝2，3，…，n 进行递推得到：

（4）引入比例及高阶信息参数，超球体单形采样样本点协方差的权重表达式与式（24）相同，Sigma样本点和均值权重分别为：

其中，由式（25）—（27）可知，与最小偏度单形采样的根指数式增长不同，超球体单形采样除了W0之外权重均为（1－W0） /（n+1），各个 Sigma 点均匀分布在半径为的球面上，数值稳定性较高，且n+2的采样规模使其具有更好的在线应用前景。

以上3种采样策略均引入比例及高阶信息参数，不仅可以保证预测协方差矩阵的半正定性，且能够通过调节其取值进行高阶信息修正。

4 计算结果及讨论

4.1 系统说明

以IEEE 30、118和300节点标准系统为例，在MATLAB 2013a环境下采用IBM-PC兼容机（intel i5-3470，3.2GHz，4G）编程实现。采样的权重 W0取为0.5，高阶信息参数β取为2，比例参数取为0.3。2n+1采样策略的PEM和进行6000次MCS抽样的求解输出作为UT方法计算结果的参考标准。

系统所接入的风电场参数如表1、2所示，光伏发电系统参数［22］如表3所示，各系统分布式电源的顺序接入情况如表4所示。

表1 IEEE 30节点系统风电场参数Table 1 Wind farm parameters of IEEE 30-bus system

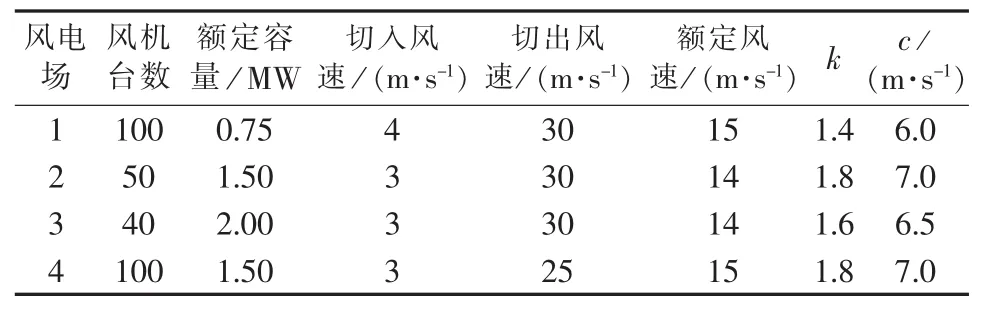
表2 IEEE 118/300节点系统风电场参数Table 2 Wind farm parameters of IEEE 118/300-bus system

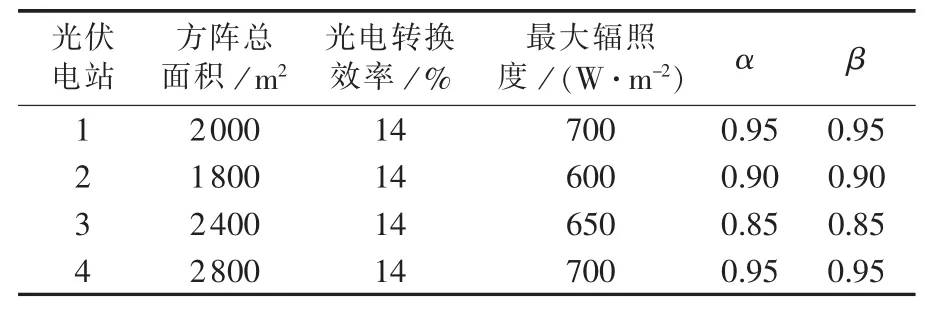
表3 光伏发电系统参数Table 3 Parameters of photovoltaic system

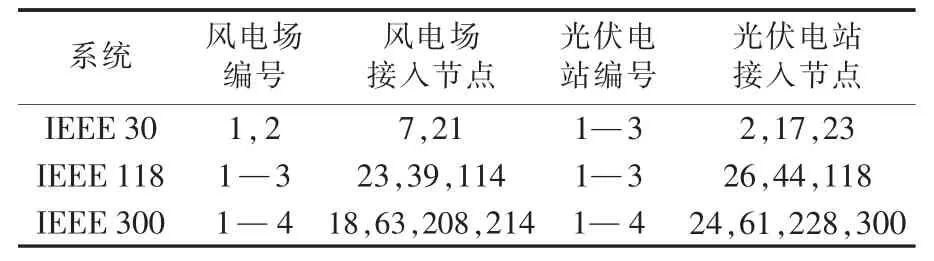
表4 分布式电源的接入情况Table 4 DG integration of different systems

4.2 不同采样策略的UT有效性

定义UT方法与MCS方法结果相对误差为：

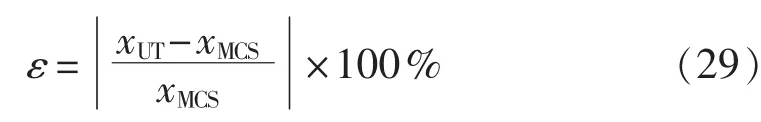
其中，xUT、xMCS分别为不同采样策略的UT和MCS方法求得的输出随机变量的均值或标准差。

表5为基于不同采样策略的UT和MCS采样规模以及收敛情况的对比；表6、7分别给出了基于不同采样策略的UT和MCS计算结果中，IEEE 30节点系统节点 10、IEEE 118节点系统节点 97、IEEE 300节点系统节点54电压幅值的相对误差和IEEE 30节点系统线路2-5、IEEE 118节点系统线路100-104、IEEE 300节点系统线路226-271有功功率的相对误差。

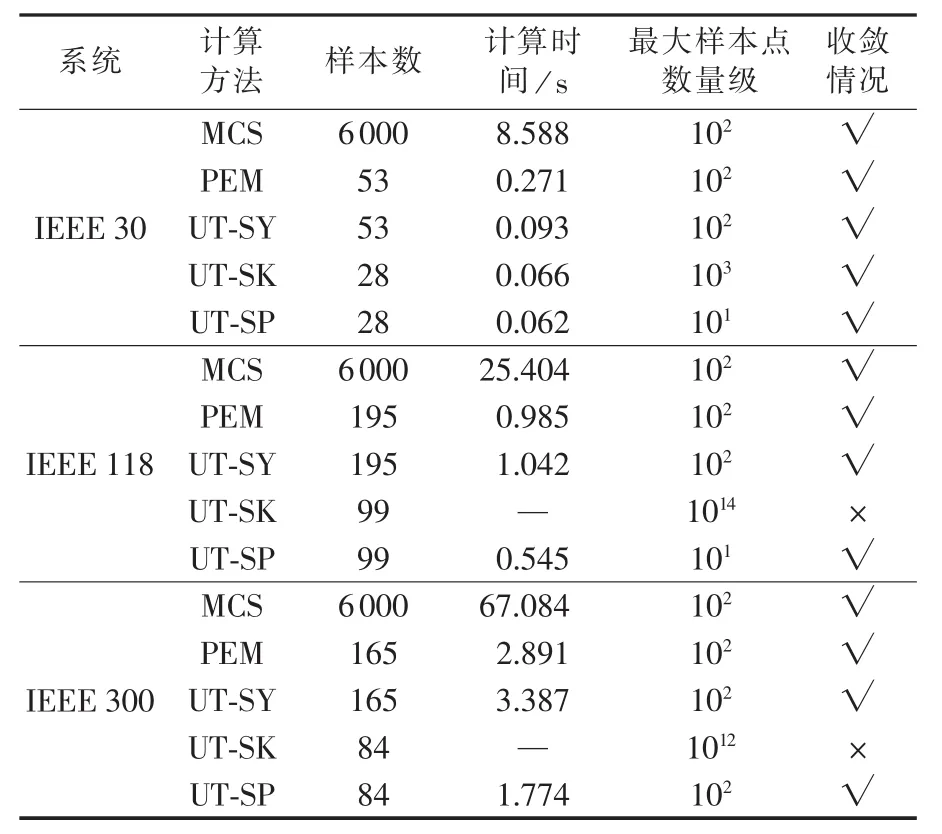
表5 收敛情况对比Table 5 Comparison of convergence performance among different systems

由式（22）和表5可知，UT-SK的采样点数值随着系统规模的增加呈现根指数式增长，对于IEEE118节点系统，输入随机变量维数为97，UT-SK方法的部分样本点数值可高达1014数量级，对于IEEE 300节点系统，输入随机变量维数为82，UT-SK方法抽取的部分采样点数值高达1012数量级，导致对应的样本无法处理。而UT-SY和UT-SP 2种方法的样本数值均不高于102数量级，具有较高的数值稳定性。虽然UT-SK和UT-SP采样规模相同，但两者抽样前的预处理不同，由于UT-SK采取根指数式抽样，较UT-SP用时稍多。

表6、表7分别为电压幅值、线路有功功率相对误差，表中电压幅值为标幺值。分析表5—7可以得到以下结论。

①UT方法处理随机潮流问题，总体误差水平较低，计算效率可提高近百倍。

②UT-SY与2n+1采样策略的PEM样本规模相同，求解精度、时间、收敛性能等都相当接近，对于IEEE 118节点系统，两者线路有功均值计算误差均约为0.06%；为避免下文图中2种方法的结果分布曲线重叠，故省略PEM的图示对比结果。

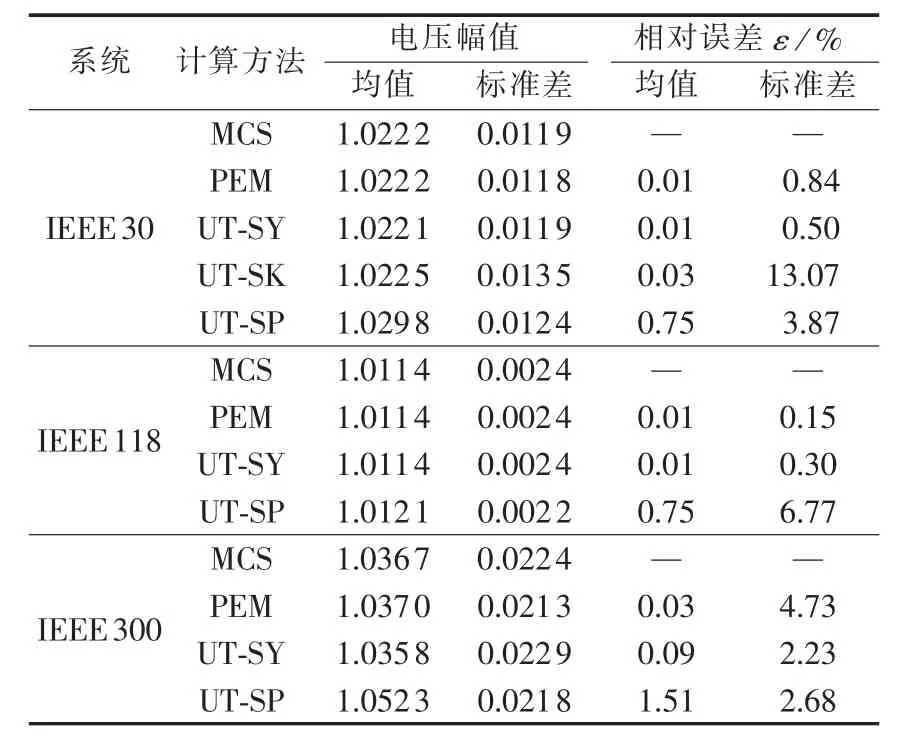
表6 电压幅值相对误差Table 6 Comparison of relative errors of voltage magnitude among different systems

表7 线路有功功率相对误差Table 7 Comparison of relative errors of line active power flow among different systems

③对于IEEE 300节点系统，UT-SY的均值计算误差可低至0.09%，用时仅为MCS方法的5.05%。

④与UT-SP相比，UT-SK的均值相对误差较小，但标准差的相对误差较大。主要因为UT-SK只抽取n+2个非对称样本，且样本点根指数式分布，数值稳定性较低，而UT-SP二阶以上的高阶信息误差较大，均值精度相对略低。

⑤UT-SK和UT-SP方法的计算速度相对较快，所以如果系统实时性要求较高，对于规模不大的IEEE 30节点系统，可优先考虑UT-SK和UT-SP策略，对于接近或超过IEEE118节点的系统，可选用UT-SP方法，以更接近在线应用的需求。

图1、2分别为各方法求解IEEE 30节点系统得到的节点10电压幅值和线路2－5有功功率的概率密度曲线，图中节点10电压幅值为标幺值。节点10的电压幅值均值为1.022 p.u.，标准差为0.012 p.u.，主要于0.98～1.07 p.u.呈高斯分布；线路2-5有功功率主要高斯分布于40.0～73.0 MW。据此可求得节点10的电压幅值在1.00～1.04 p.u.之间的概率为0.8996，线路2-5的有功功率在50.0～62.5 MW的概率为0.8065。所以，通过对UT结果的处理，求得的概率信息可为评估含分布式电源系统的线路安全情况、电压水平等提供更为可靠的参考。且UT-SY与MCS的拟合度最高，结果令人满意；UT-SK方法均值拟合精度高于UT-SP，但标准差精度略低。

图3为IEEE118节点系统节点97电压幅值的累积概率分布曲线，图中节点97电压幅值为标幺值；图4为IEEE300节点系统线路226-271有功功率的概率密度分布曲线。可以看出：线路226-271的有功功率主要在4～14 MW之间分布，求得其在7～11 MW之间的概率为0.7940。且UT-SY方法的拟合度依然较高，可以满足实际应用的需求；UT-SK方法由于数值稳定性问题无法处理这2个较大系统。MCS能够从大量数值结果中确定仿真变量的概率分布类型，将MCS与UT方法对比使用，能更好地综合两者在准确性和求解效率方面的优势。

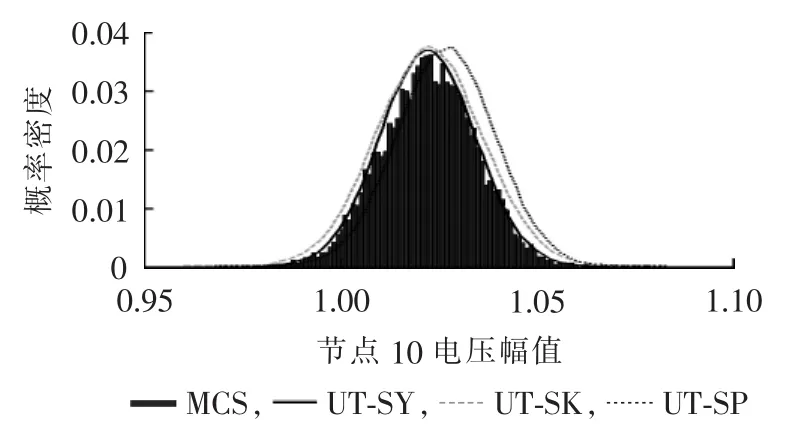
图1 IEEE 30节点系统节点10电压幅值的概率密度分布Fig.1 Probability density distribution of voltage magnitude at Bus 10 of IEEE 30-bus system

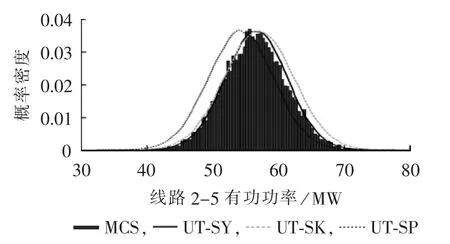
图2 IEEE 30节点系统线路2-5有功功率的概率密度分布Fig.2 Probability density distribution of active power flow of Line 2-5 of IEEE 30-bus system

4.3 相关性对随机潮流的影响

受到天气条件的影响，相近区域的风电场的风速、光伏发电系统的光照强度具有一定相关性，且此区域的电力用户的消费行为也与天气条件有关。于是地理位置邻近的风速、光照强度以及负荷的相关性对系统运行特性的影响不容忽略。

图3 IEEE 118节点系统节点97电压幅值的累积概率分布Fig.3 Cumulative probability distribution of voltage magnitude at Bus 97 of IEEE 118-bus system

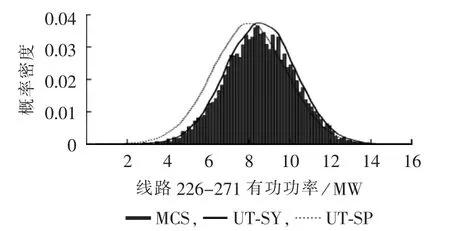
图4 IEEE 300节点系统线路226-271有功功率的累积概率分布Fig.4 Cumulative probability distribution of active power flow of Line 226-271 of IEEE 300-bus system

图5 IEEE 300节点系统相关性对线路有功功率均值的影响Fig.5 Effect of IEEE 300-bus system correlation on mean value of line active power flow

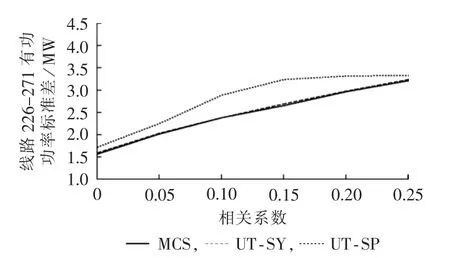
图6 IEEE 300节点系统相关性对线路有功功率标准差的影响Fig.6 Effect of IEEE 300-bus system correlation on standard deviation of line active power flow

图5、6分别给出了风速、光照强度和负荷等输入随机变量相关系数从0到0.25变化时，IEEE300节点系统线路226-271有功功率的统计特性。可以看出：随机变量相关系数增长时，有功功率均值基本保持不变，而标准差明显增加。主要原因是相关性使得各随机变量的波动具有同步性，进而增强了电网运行的总体波动性，表现为输出随机变量的标准差增加。考虑随机变量的相关性后，UT方法的均值计算结果都非常精确，其中，UT-SP的标准差的计算误差偏大，UT-SY方法的精度依然较高。

5 结论

本文将3种采样策略的UT方法应用于含分布式电源系统的随机潮流计算，可得出以下结论。

a.通过本文的比较和分析，可根据系统规模及实际应用中对结果精度、实时性的要求，综合选择适当的采样策略，且3种采样策略的UT方法计算用时均较少。

b.对称采样策略适用于求解多随机变量、大规模的电力系统的随机潮流问题，具有较高的数值稳定性，除用时相对稍多外，精度最高，性能出色。

c.最小偏度单形采样策略由于采取根指数式抽样而无法处理高维系统，标准差精度偏低。超球体单形采样策略与最小偏度单形采样策略的计算用时相当，但均值误差稍大。

状态监测对电力系统的安全运行具有重要意义，随着分布式电源的接入，配电网的不确定性因素日益增加，所以将状态监测拓展到随机领域可为系统运行状况评估提供更为全面的参考。故后续研究将把UT方法应用于含分布式电源的配电网随机状态监测。

［1］BORKOWSKA B.Probabilistic load flow［J］.IEEE Transactions on Power Apparatus and Systems，1974，93（3）：752-759.

［2］王成山，郑海峰，谢莹华，等.计及分布式发电的配电系统随机潮流计算［J］. 电力系统自动化，2005，29（24）：39-44.WANG Chengshan，ZHENG Haifeng，XIE Yinghua，et al.Probabilistic power flow containing distributed generation in distribution system［J］.Automation of Electric Power Systems，2005，29（24）：39-44.

［3］方斯顿，程浩忠，徐国栋，等.基于Nataf变换和准蒙特卡洛模拟的随机潮流方法［J］. 电力自动化设备，2015，35（8）：38-44.FANG Sidun，CHENG Haozhong，XU Guodong，et al.Probabilistic load flow method based on Nataftransformation and quasi Monte Carlo simulation［J］.Electric Power Automation Equipment，2015，35（8）：38-44.

［4］GUSTAVO V，ANDRIJA T S，VLADIMIR T.Stochastic monitoring of distribution networks including correlated input variables［J］.IEEE Trans on Power Systems，2013，28（1）：246-255.

［5］MORALES J M，PEREZ-RUIZ J.Point estimate schemes to solve the probabilistic power flow［J］.IEEE Trans on Power Systems，2007，22（4）：1594-1601.

［6］杨欢，邹斌.含相关性随机变量的概率潮流三点估计法［J］.电力系统自动化，2012，36（15）：51-56.YANG Huan，ZOU Bin.A three-pointestimate method for solving probabilistic power flow problems with correlated random variables［J］.Automation of Electric Power Systems，2012，36（15）：51-56.

［7］吴晨曦，文福拴，陈勇，等.含有风电与光伏发电以及电动汽车的电力系统概率潮流［J］. 电力自动化设备，2013，33（10）：8-15.WU Chenxi，WEN Fushuan，CHEN Yong，et al.Probabilistic load flow of power system with WFs，PVs and PEVs［J］.Electric Power Automation Equipment，2013，33（10）：8-15.

［8］MORALES J M，BARINGO L，CONEJO A J，et al.Probabilistic power flow with correlated wind sources［J］.IET Generation，Transmission&Distribution，2010，4（5）：641-651.

［9］丁明，李生虎，黄凯.基于蒙特卡罗模拟的概率潮流计算［J］.电网技术，2001，25（11）：10-14.DING Ming，LI Shenghu，HUANG Kai.Probabilistic load flow analysisbased on Monte-Carlo simulation［J］.PowerSystem Technology，2007，25（11）：10-14.

［10］RODRIGUES A B，da SILVA M G.Probabilistic assessment of available transfer capacity based on Monte Carlo method with sequential simulation［J］.IEEE Trans on Power Systems，2007，22（1）：484-492.

［11］USAOLA J.Probabilistic load flow with wind production uncertainty using cumulants and Cornish-Fisher expansion［J］.International Journal of Electrical Power& Energy Systems，2009，31（9）：474-481.

［12］胡泽春，王锡凡，张显，等.考虑线路故障的随机潮流［J］.中国电机工程学报，2005，25（24）：26-33.HU Zechun，WANG Xifan，ZHANG Xian，etal.Probabilistic load flow method considering branch outages［J］.Proceedings of the CSEE，2005，25（24）：26-33.

［13］蔡德福，石东源，陈金富.基于多项式正态变换和拉丁超立方采样的概率潮流计算方法［J］. 中国电机工程学报，2013，33（13）：92-100.CAI Defu，SHI Dongyuan，CHEN Jinfu.Probabilistic load flow calculation method based on polynomial normal transformation and latin hypercube sampling［J］.Proceedings of the CSEE，2013，33（13）：92-100.

［14］USAOLA J.Probabilistic load flow in systemswith wind generation［J］.IET Generation，Transmission&Distribution，2009，3（12）：1031-1041.

［15］陈雁，文劲宇，程时杰.考虑输入变量相关性的概率潮流计算方法［J］. 中国电机工程学报，2011，31（22）：80-87.CHEN Yan，WEN Jinyu，CHENG Shijie.Probabilistic load flow analysis considering dependencies among input random variables［J］.Proceedings of the CSEE，2011，31（22）：80-87.

［16］JULIER S.The scaled unscented transformation［C］∥Proceedings of the American Control Conference.Anchorage，AK，USA：［s.n.］，2002：4555-4559.

［17］JULIER S，UHLMAN J.Unscented filtering and nonlinear estimation［J］.Proceedings of the IEEE，2004，92（3）：401-422.

［18］JULIER S，UHLMAN J.A new method for nonlinear transformation of means and covariances in filters and estimators［J］.IEEE Trans on Automation Control，2000，45（3）：477-482.

［19］鲍海波，韦化.基于无迹变换的含大规模风电场电力系统概率最优潮流计算［J］. 电力系统自动化，2014，38（12）：46-53.BAO Haibo，WEIHua.Probabilisticallyoptimalpowerflow computation in power system including large-scale wind farms based on unscented transformation［J］.Automation of Electric Power Systems，2014，38（12）：46-53.

［20］SAEED J，CRISTIAN L，FADALIM S.Stateestimation of induction motor drives using the unscented Kalman filter［J］.IEEE Trans on Industrial Electronics，2012，59（11）：4207-4216.

［21］MORTEZA A，MAHMUD F，FARROKH A.Probabilistic load flow in correlated uncertain environment using unscented transformation［J］.IEEE Trans on Power Systems，2012，27（4）：2233-2241.

［22］王敏，丁明.考虑分布式电源的静态电压稳定概率评估［J］.中国电机工程学报，2010，30（25）：17-22.WANG Min，DING Ming.Probabilistic evaluation of static voltage stability taking account of distribute generation［J］.Proceedings of the CSEE，2010，30（25）：17-22.

［23］KARAKISH，CHEDID R B，RAMADAN R.Probabilistic performance assessment of autonomous solar-wind energy conversion systems［J］.IEEE Trans on Energy Conversion，1999，14（3）：766-772.

［24］鲍海波，韦化.考虑风电的电压稳定概率评估的随机响应面法［J］. 中国电机工程学报，2012，32（13）：77-85.BAO Haibo，WEI Hua.Stochastic response surface method for probabilistic evaluation of voltage stability considering wind power［J］.Proceedings of the CSEE，2012，32（13）：77-85.

［25］卫志农，孙国强，庞博.无迹卡尔曼滤波及其平方根形式在电力系统动态状态估计中的应用［J］.中国电机工程学报，2011，31（16）：74-80.WEI Zhinong，SUN Guoqiang，PANG Bo.Application of UKF and SRUKF to power system dynamic state estimation ［J］.Proceedings of the CSEE，2011，31（16）：74-80.

［26］JULIER S，UHLMAN J.Reduced Sigma point filters for the propagation of means and covariances through nonlinear transformations［C］∥Proceedings of the American Control Conference.Anchorage，AK，USA：［s.n.］，2002：887-892.

［27］JULIER S.The spherical simplex unscented transformation［C］∥Proceedings of the American Control Conference.Denver，Colorado，USA：［s.n.］，2003：2430-2434.