电力系统源网间协同的经济调度模型及矩量半定规划法

孙东磊，韩学山，张 波

（山东大学 电网智能化调度与控制教育部重点实验室，山东 济南 250061）

0 引言

电力系统经济调度的概念可追溯至20世纪20年代，电力系统中负荷的时空分布变化是经济调度问题产生的根本原因。实际上，调度主要是为应对负荷的变化，预先对机组出力进行优化决策，促使发电与负荷按预知轨迹平衡，其实质为固定电网结构下发电跟踪负荷的经济决策。经过近百年的发展，电力系统经济调度研究在理论和实践上已相对成 熟［1-7］。

然而，随着电力市场竞争机制的不断推进，电力负荷呈现电动汽车、储能等形式多元化发展，以及风光等可再生能源发电以分布或集中形式大规模地且有迅猛发展趋势地并入电网，电力系统中输配交融、电能双向流动，源（发电与负荷）网间呈现日趋交织纠结的矛盾，电网构架出现与其不相适应的非同调现象，即输电阻塞问题，该问题仅靠改变发电方式已难以抑制。为有效缓解这一矛盾，出现了改变电网元件状态（电网络重构）来解决这一问题的研究，提出考虑电网拓扑控制的安全校正CS（Corrective Switching）方法［8-9］，以及融入电网拓扑优化的经济调度 OTS（Optimal Transmission Switching）方法［10-13］。

为保证电网可靠运行同时兼顾电力供求增长等因素，实际规划的电网拓扑架构及其传输容量均处于冗余状态，但实际电网运行中并不是冗余度越高，系统越可靠，这就是电力系统可靠性问题的非同调现象［14］，即一个元件从系统中缺省反而产生一个更可靠的系统状态。新形势下电力系统中被动的源（负荷以及可再生能源发电等）呈现复杂多变的情形，固定电网结构将使经济调度中源网间关系更多地处于冲突状态［15］。实际上，经济调度中源网间的矛盾主要是由于电网络的基尔霍夫电压定律约束制约了环网中部分输电元件传输容量的发挥，使得经济发电机组发电外送能力受到限制，严重时威胁源平衡的实现，即对应经济调度无可行解的情况。因此，调度决策中有选择地对电网拓扑进行调整不仅有助于源平衡的实现，而且对提高系统运行的经济性具有重要作用。本文中电网拓扑调整主要考虑电力传输线路的投切。不同于节点上设备的投运决策，电网支路投切决策需考虑电网物理规律，即基尔霍夫定律（KCL和KVL）。电网支路运行范围约束实则为条件约束，即若运行则需遵循电网约束，若停运则不需遵循电网约束。针对此条件约束，本文以互补形式予以表达，由此得到的源网间协同的经济调度模型为混合整数非线性规划模型，其表现为非线性、不可微及非凸特性，求取其全局最优解非常困难。对此，本文从新的视角出发，由半定规划SDP（Semi-Definite Programming）凸松弛方法将其转换为凸优化问题求解。

SDP［16］是指线性函数在对称矩阵的仿射组合半正定约束下的极值问题，是特殊的锥优化问题，属于凸规划范畴。经过近20 a的快速发展，半定规划理论研究逐渐成熟，且已被应用于｛0，1｝经济调度［17］、最优潮流［18-19］、机组组合［20］以及状态估计［21］等电力系统优化问题求解。然而，上述问题本身为非凸非线性规划问题，而将其松弛为SDP凸规划问题时，实则为忽略了变量矩阵的秩为1约束［22］，但优化得到的结果通常无法满足秩为1的要求，因此其往往不能得到有效的最优解。尽管一些学者针对该问题对SDP在求解电力系统优化问题中的适用范围和应用条件进行了研究［22-24］，电力系统优化问题的SDP松弛的秩为1约束的局限性至今仍没有得到有效解决。为此，文献［25］针对电力系统全局优化问题的求解困境，引入矩量理论，提出了一种矩量半定规划MSDP（Moment-based SDP）方法，并成功应用于求取｛0，1｝经济调度和最优潮流问题的全局最优解，取得了令人满意的效果。MSDP的思想由法国数学家Lasserre于2001年首次提出，其是将多项式优化问题转化为矩量空间的SDP问题，通过不断提高松弛阶次，即增大矩量矩阵的阶次，最终可逼近到问题的全局最优解［26-28］。

本文将MSDP方法引入电力系统源网间协同的经济调度模型求解中，根据MSDP凸松弛方法构造源网间协同的经济调度问题的MSDP模型，基于MATLAB平台由SDP优化器SDPA［29］予以求解。最后，通过算例分析对本文方法的有效性进行了验证。

1 电力系统源网间协同的经济调度模型

电力系统源网间协同的经济调度模型是在直流潮流的条件下以追求经济性最优为目标，同时满足系统运行的物理和技术约束条件，以对发电机组有功功率、电网元件状态进行预先安排。为便于表述，本文中统一以上、下划线分别表示相应变量的上、下限。

1.1 目标函数

其中，NG为发电机组集合；Pg为机组g有功功率；cg为机组g线性发电成本系数。

1.2 约束条件

a.发电机组有功功率范围约束：

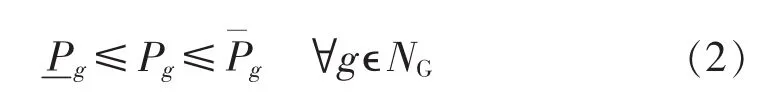
其中，g和g分别为发电机组g有功功率的上、下限。

b.电网支路运行范围约束：

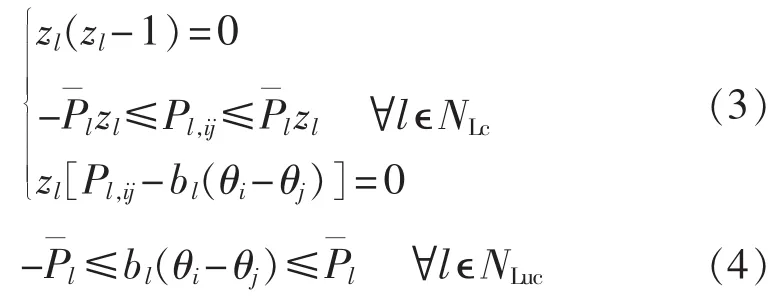
其中，zl和bl分别为支路l的运行状态和电纳，zl=0表示支路停运，zl=1表示支路在线运行；Pl，ij为支路l有功功率，其首、末端节点分别为节点 i、j，θi和 θj分别为其电压相角；l为输电支路l传输容量上限；NLc和NLuc分别为可控、不可控电网支路集合。c.节点功率平衡约束（KCL）：

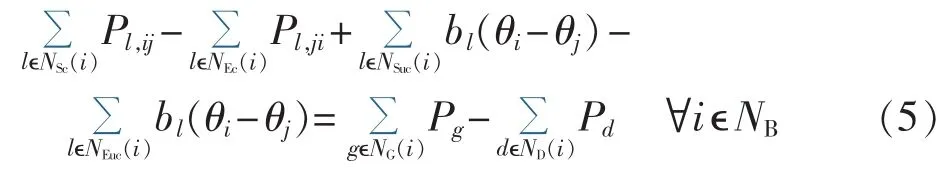
其中，Pd为负荷 d 有功功率；NB为节点集合；NG（i）和ND（i）分别为节点 i上的发电机和负荷集合；NSc（i）、NEc（i）、NSuc（i）和 NEuc（i）分别为以节点 i为首、末端节点的可控、不可控支路集合。

需说明的是，式（3）所示混合整数非线性互补约束由于违反了在可行点上的Mangasarian-Fromovitz约束条件［30］，采用传统的数学规划方法求解是极其困难的。

2 模型求解方法

2.1 SDP

SDP是在满足约束为对称矩阵的仿射组合半正定的条件下使线性函数极大（极小）化的问题，其为线性规划在矩阵空间中的推广，其中变量的非负性以变量矩阵的半正定性取代，约束以线性矩阵不等式（LMI）形式表达。SDP的原问题可表示为：

其中，vi（i=1，2，…，n）为求解的变量，n 为未知变量的个数；ci为目标函数价值系数；S为m×m阶对称矩阵，m为约束矩阵的维数；符号为矩阵的半正定运算；Fi（i=1，2，…，n）为 m×m 阶系数矩阵；F0为m×m阶常数项矩阵。式（6）的对偶问题为：

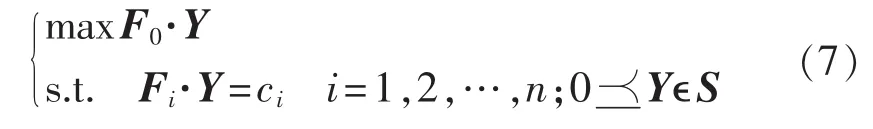
其中，符号“·”为矩阵迹运算。

SDP的求解与线性规划相似，可由理论上较成熟的多项式时间的原对偶内点法求解。求解SDP问题式（6）的对数障碍函数问题，即：

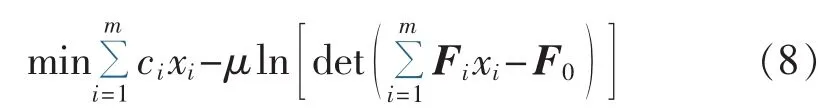
其中，μ为对数壁垒参数；det（·）表示矩阵行列式函数。式（8）的一阶 KKT（Karush-Kuhn-Tucker）最优性条件为：

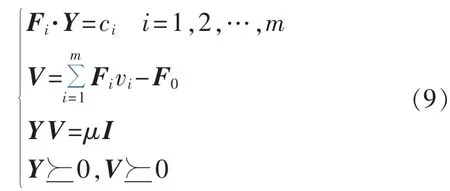
其中，I为m×m阶单位矩阵。

由牛顿法求解式（9）所示KKT方程，迭代求解直到对偶间隙Gap=（Y·V）/m满足收敛条件。

2.2 MSDP凸松弛

MSDP凸松弛是通过变量扩展的形式将非凸多项式优化问题映射为矩量空间的SDP凸问题进行求解［27］。MSDP凸松弛的核心在于多项式函数的线性矩量表达，其是将矩量的定义引入函数的线性表达中，从而将问题映射到矩量空间。任一多项式函数 q（X）的矩量为其关于概率测度μ（X）的积分，即：

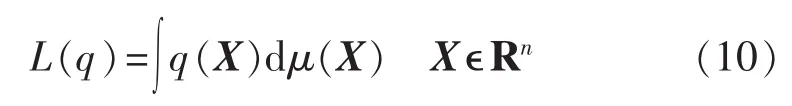
针对以下多项式优化问题：

其中，nf、nhi为相应多项式函数的单项式个数；fk、hik为相应单项式系数；X 为 n 维变量，X=（x1，…，xn）T；单项式（N 为非负整数集合），αk用以标记第k个单项式，记为xα的阶数，则式（11）的 r阶松弛模型为：

其中，s（2r）为变量拓展后对应的矩量变量总数，，y 为矩量变量，Mr（y）为矩量矩阵，Md（hiy）为不等式约束局部矩阵，其可分别展开为：

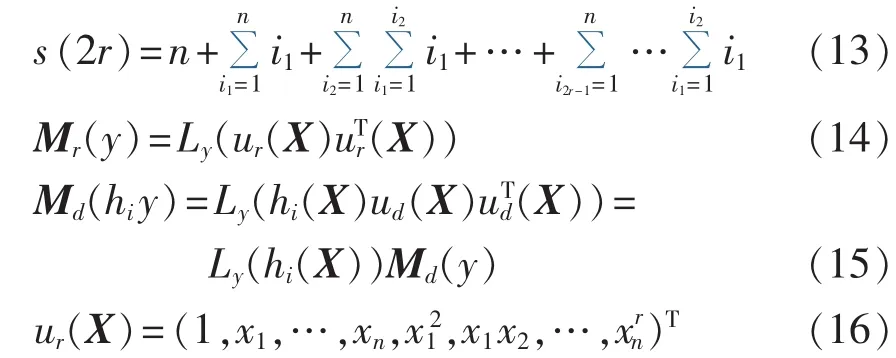
其中，ur（X）为原问题变量的 r阶扩展向量；Ly（X）表示对矩阵X中的每个元素取矩量运算。矩量矩阵半正定约束是变量扩展后的固有约束，反映原问题变量之间的关系，而局部矩阵半正定约束则反映了与不等式约束相关的部分变量之间的关系。

2.3 模型求解

本文模型为二阶多项式优化模型，模型中变量向量X和原问题变量个数num分别为：

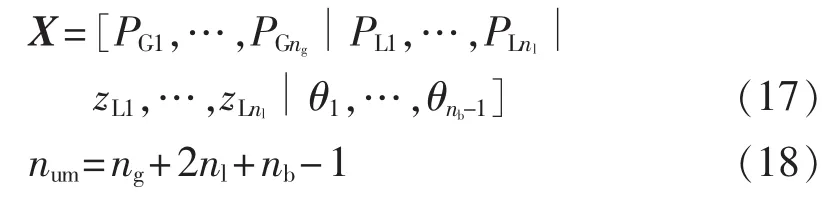
其中，PG1、…、PGng为各发电机组有功功率；PL1、…、PLnl为各输电支路有功功率；zL1、…、zLnl为各输电支路运行状态；θ1、…、θnb-1为各输电支路有功功率；ng、nl和nb分别为发电机数、可控支路数和节点数。

文献［25］试验表明，对于电力系统优化问题，一般二阶松弛就能获得问题的最优解。本文主要分析二阶松弛情况，为体现本文算法的有效性，分析中以SDP松弛方法作比较。实际上，SDP松弛可视为MSDP的一阶松弛情况。SDP松弛和MSDP二阶松弛后的变量数分别为 s（2）和 s（4）。

模型求解具体流程如下：

a.将本文源网间协同的经济调度模型表示为式（11）所示的多项式函数优化形式；

b.MSDP二阶松弛得到式（12）所示的SDP问题；

c.求解式（12）所示SDP问题，得到矩量最优解，然后将其还原至原问题的解空间，由此求得各发电机组有功功率、电网元件状态。

3 算例分析

算例仿真在主频为3.1 GHz、内存为16 GB的计算机上实现，基于MATLAB平台由SDP优化器SDPA进行求解。计算中功率基准值为100 MV·A。

3.1 算例1

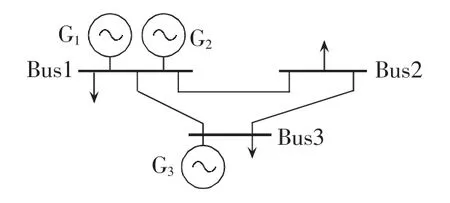
图1 3节点电力系统接线图Fig.1 Diagram of 3-bus power system

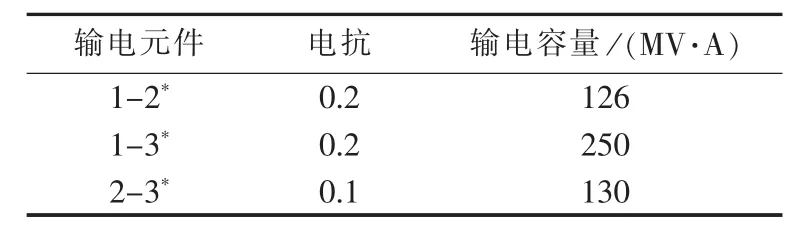
表1 3节点系统元件参数Table 1 Line parameters of 3-bus power system

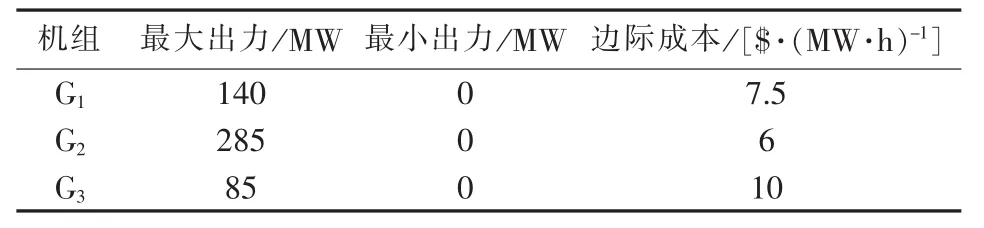
表2 3节点系统发电机组参数Table 2 Generator parameters of 3-bus power system

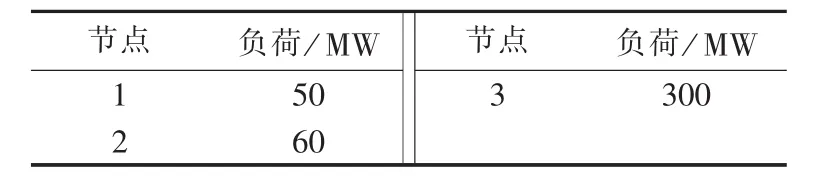
表3 3节点系统负荷数据Table 3 Load data of 3-bus power system

以图1所示的3节点电力系统为例，电网元件参数、发电机组参数以及某系统负荷模式数据等见表1—3，表1中电抗为标幺值，后同。不考虑电网传输容量制约的单母线模型前提下的经济调度结果称为最经济源平衡方式，然而，最经济源平衡方式有可能因电网制约而无法实现。3节点电力系统的最经济源平衡方式如表4所示，发电总成本为2647.5$/h，经直流潮流计算，可知输电元件1-2潮流为156 MW，过载30 MW，易见实际中因电网元件传输容量制约导致最经济源平衡方式无法实现。由此在给定电网构架下，实施安全经济调度的结果如图2所示，图中箭头旁数字表示以100 MV·A为功率基准值的功率标么值。图2所示方式对应成本为2835$/h，比最经济源平衡方式增加了187.5$/h，究其原因是输电元件1-2的输电容量约束限制了经济机组G1的出力，即较经济发电机组G1的发电外送能力受到限制，从而造成边际成本更高的机组G3出力增加。对此，以本文源网间协同的经济调度模型，并以SDP松弛方法和MSDP二阶松弛法分别求解予以分析，半定松弛矩阵 M1（y）和二阶矩量矩阵 M2（y）分别如表 5 和表6所示。

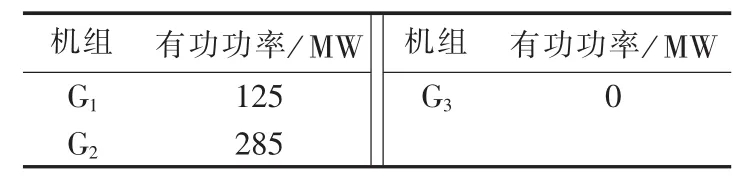
表4 3节点系统最经济源平衡方式Table 4 Most economic pattern of sourcebalancing for 3-bus power system

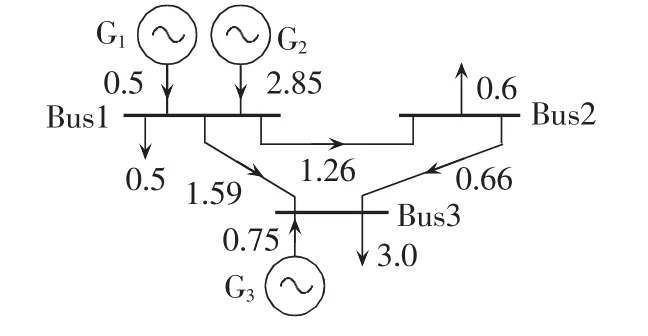
图2 3节点系统安全经济调度模式运行图Fig.2 Operational chart of security-constrained economic dispatch pattern for 3-bus power system

表5 中，P1、P2和 P3分别为发电机组 G1、G2和 G3有功功率，P1-2、P1-3和 P2-3分别为支路 1-2、1-3和 2-3 有功功率，z1-2、z1-3和 z2-3分别为支路 1-2、1-3 和2-3运行状态。由表5可看出，半定松弛矩阵M1（y）中多行是严格对角占优，显然其秩远大于1，经计算秩为12，无法得到原问题的最优解。由表6可以看出，二阶矩量矩阵M2（y）中任意2行之间存在倍数关系，因此其秩为1，由此可得考虑电网制约的系统最优运行方式如图3所示。

由图3可以看出，最优状态下，开断支路2-3，释放了发电机组G1的发电外送能力，直到支路1-3达到传输容量上限，负荷3的功率缺额由机组G3满足。

3.2 算例2

算例2分析基于图4所示的某实际电力系统。表7—9分别给出了该系统电网元件参数、发电机组参数、某负荷模式数据。该模式下风电场输出功率为30 MW。最经济源平衡方式如图5所示，发电总成本为16 574$/h，可见输电元件4-5潮流过载，易见实际中因电网元件传输容量制约最经济源平衡方式无法实现。由此若在给定电网构架下，实施安全经济调度，经计算无可行解，究其原因为线路4-5传输容量限制导致同一回路中的输电线路1-7、1-2的输电能力不能充分发挥，造成功率传输瓶颈，由于该模式下风电场输出功率较小，切负荷情况必不可免。对此，以本文源网间协同的经济调度模型，并以MSDP二阶松弛法求解予以分析，二阶矩量矩阵 M2（y）如表 10 所示。

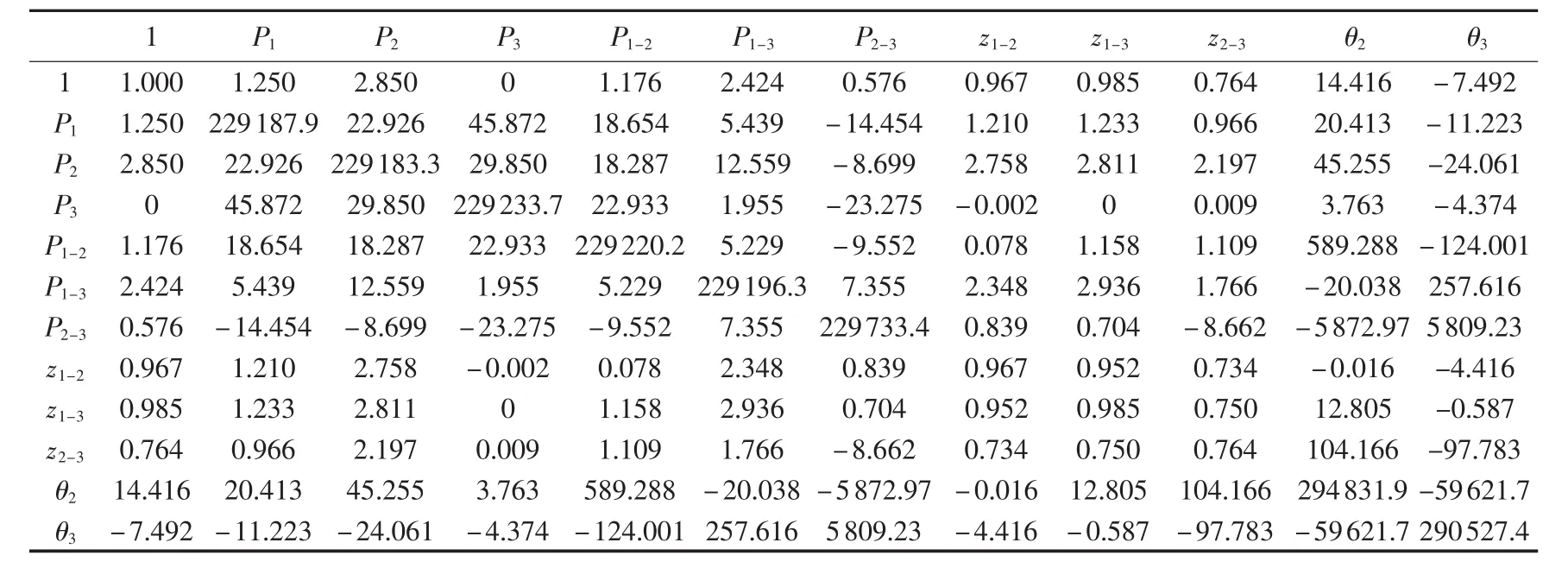
表5 算例1半定松弛矩阵M1（y）Table 5 Semi-definite relaxation matrix M1（y） of Case 1

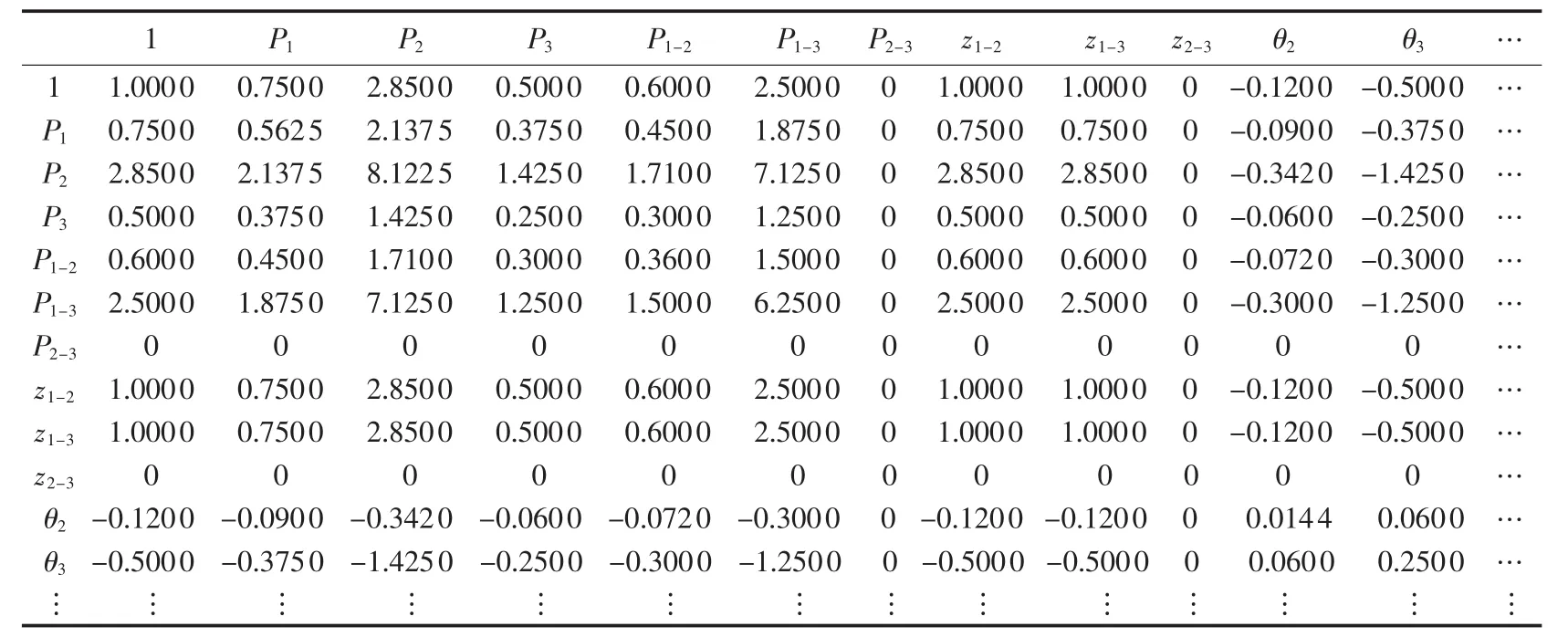
表6 算例1二阶矩量矩阵M2（y）Table 6 Second-order moment matrix M2（y） of Case 1

图3 3节点系统源网间协同的经济调度模式运行图Fig.3 Operational chart of economic dispatch pattern with source-network synergy for 3-bus power system

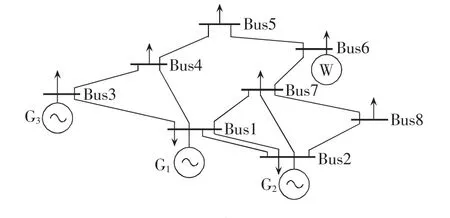
图4 实际电网接线图Fig.4 Diagram of an actual power system

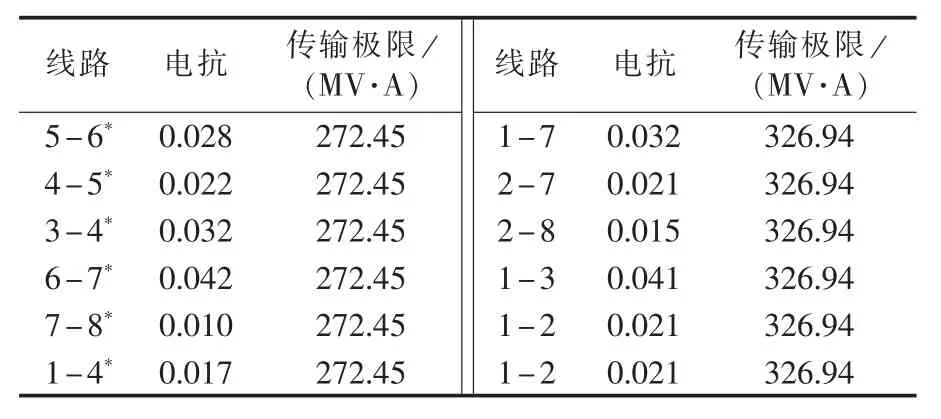
表7 实际系统电网元件参数Table 7 Line parameters of an actual power system

表8 实际系统机组参数Table 8 Generator parameters of an actual power system

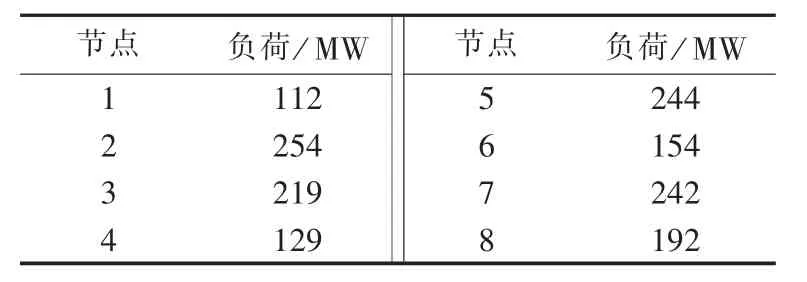
表9 实际系统负荷数据Table 9 Load data of an actual power system

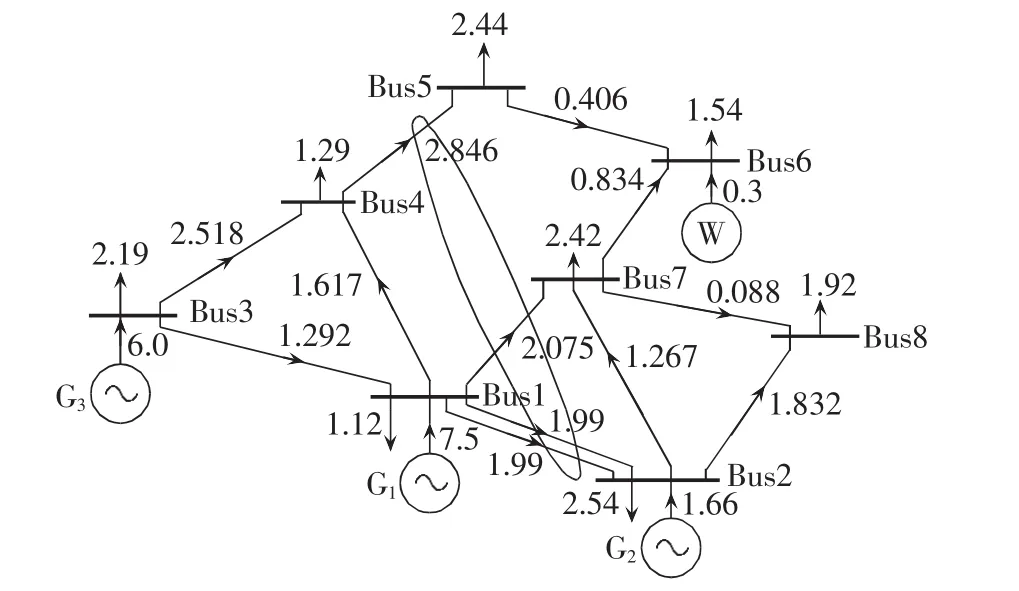
图5 实际系统最经济源平衡方式图Fig.5 Most economic pattern of source-balancing for an actual power system

表10 算例2二阶矩量矩阵M2（y）Table 10 Second-order moment matrix M2（y） of Case 2

由表10可看出，二阶矩量矩阵M2（y）中任意2行之间存在倍数关系，因此其秩为1，由此可得考虑电网制约的系统最优运行方式如图6所示。由图6可看出，最优状态下，开断支路5-6，释放了发电机组G3的发电外送能力，最经济源平衡方式得以实现。

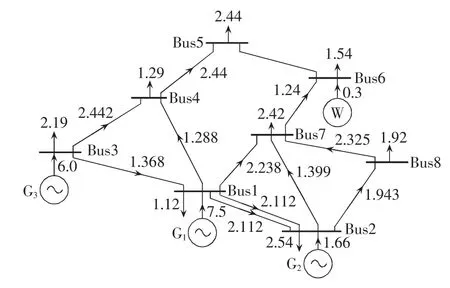
图6 实际系统源网间协同的经济调度模式运行图Fig.6 Operational chart of economic dispatch pattern with source-network synergy for an actual power system

3.3 计算性能分析和讨论

MSDP的优点在于其全局寻优能力，但其是以扩展变量的形式实现的，势必会降低计算效率，表11和表12分别给出了本文两算例的计算性能以及算例2计算性能随可控支路个数变化情况。

表11 算例计算性能Table 11 Computational performance of cases

表12 算例2计算性能随可控支路个数变化情况Table 12 Computational performance of Case 2 for different controllable line quantities

由表11和表12可以看出，由于MSDP松弛对变量进行了扩展，随着原问题变量个数的增大，MSDP求解时占用的内存以及计算时间非线性增加，计算复杂度非线性增加。对于算例2而言，其计算复杂性已非常高，因此，MSDP求解难以满足更大规模系统的应用需求。由此本文模型及其求解性能需要进一步提高以满足实际系统应用需求。

关于如何提高求解源网间协同的经济调度问题的MSDP法的计算性能，笔者打算从以下几个方面着手予以解决：首先，就问题本身特点出发给定一定规则进行约束缩减，如保证电网连通性［31］，则可缩小电网可控范围，以减小问题求解规模；其次，从SDP数值计算领域［32］出发，利用成熟的稀疏处理技术以提高算法的计算效率，并将其应用于源网间协同的经济调度问题的求解；此外，电力系统计算本身也有可以挖掘的稀疏处理的空间［33］，如对原问题变量的排列顺序进行优化，可一定程度上提高计算效率。受篇幅所限，以上思路的具体实现笔者将另文详细探讨。

4 结论

新形势下源网间呈现日趋交织纠结的矛盾，对此，本文提出一种电力系统源网间协同的经济调度模型，模型中将电网设备状态纳入调度决策，能够扩大调度决策解的空间，提高电力系统源平衡能力以及电网运行的经济性；针对源网间协同的经济模型求解困难、难以求得全局最优解的情况，本文首次将MSDP法引入考虑电网拓扑优化的源网间协同的经济调度研究中，算例分析表明该方法具有全局寻优能力，对最大化系统源平衡能力和电网运行经济性具有重要意义。

本研究是电力系统协同调度的重要组成部分。进一步会将这一方法拓展到考虑机组启停决策的源网间协同的经济调度优化之中，以在长时间尺度内揭示源网间协同的经济调度的价值，预期会促进新形势下电网调度理论的进展。此外，如何保证系统满足一定的可靠性指标以及提高所提方法的求解效率以使其能够满足实际大规模系统应用需求仍需要进一步的深入研究。

［1］WOOD A J，WOLLENBERG B F．Power generation，operation，and control［M］．影印版.北京：清华大学出版社，2003：29-123，209-230.

［2］CARPENTIER J.Contribution a l’etude du dispatching economique［J］.Bulletin de la Societe Francaise des Electriciens，1962，3（8）：431-447．

［3］XU G，GALIANA F D，LOW S.Decoupled economic dispatch using the participation factors load flow［J］.IEEE Trans on Power Apparatus and Systems，1985，PAS-104（6）：1377-1384.

［4］韩学山．动态优化调度的积留量法［D］．哈尔滨：哈尔滨工业大学，1994．HAN Xueshan.Accumulation variable method in dynamic optimal dispatch［D］.Harbin：Harbin Institute of Technology，1994.

［5］张伯明，吴文传，郑太一．消纳大规模风电的多时间尺度协调的有功调度系统设计［J］．电力系统自动化，2011，35（1）：1-6.ZHANG Boming，WU Wenchuan，ZHENG Taiyi.Design of a multitime scale coordinated active powerdispatching system for accommodating large scale wind power penetration［J］.Automation of Electric Power Systems，2011，35（1）：1-6.

［6］钟世民，韩学山，刘道伟．计及校正控制的安全约束最优潮流的奔德斯分解算法［J］. 中国电机工程学报，2011，31（1）：65-71．ZHONG Shimin，HAN Xueshan，LIU Daowei.Benders decomposition algorithm for corrective security-constrained optimal power flow［J］.Proceedings of the CSEE，2011，31（1）：65-71.

［7］谢俊，陈凯旋，岳东，等.基于多智能体系统一致性算法的电力系统分布式经济调度策略［J］.电力自动化设备，2016，36（2）：112-117.XIE Jun，CHEN Kaixuan，YUE Dong，et al.Distributed economic dispatch based on consensus algorithm of multi agent system for power system［J］.Electric Power Automation Equipment，2016，36（2）：112-117.

［8］LI M，LUH P B，MICHEL L D.Corrective line switching with securityconstraintsforthe base and contingency cases ［J］.IEEE Trans on Power Systems，2012，27（1）：125-133.

［9］GOU B，ZHANG H.Fast real-time corrective control strategy for overload relief in bulk power systems［J］.IET Generation，Transmission&Distribution，2013，7（12）：1508-1515.

［10］O’NEILL R P，BALDICK R，HELMAN U.Dispatchable transmission in RTO markets［J］.IEEE Trans on Power Systems，2005，20（1）：171-179.

［11］FISHER E B，O’NEILL R P，FERRIS M C.Optimal transmission switching［J］.IEEE Trans on Power Systems，2008，23（3）：1346-1355.

［12］HEDMAN K W，O’NEILL R P，FISHER E B，et al.Optimal transmission switching with contingency analysis［J］.IEEE Trans on Power Systems，2009，24（3）：1577-1586.

［13］HEDMAN K W，FERRIS M C，O’NEILL R P，et al.Co-optimization of generation unit commitment and transmission switching with N-1 reliability［J］.IEEE Trans on Power Systems，2010，25（2）：1052-1063.

［14］李文沅，周家启，谢开贵.在输电线和变电站组合联结网络中的非同调现象［J］. 中国电机工程学报，2006，26（14）：7-11.LI Wenyuan，ZHOU Jiaqi，XIE Kaigui.Non-coherence phenomenon in combinative transmission line and substation configurations［J］.Proceedings of the CSEE，2006，26（14）：7-11.

［15］刘国静，韩学山，杨明.经济调度中源网间的三种状态分析及验证［J］. 电网技术，2013，37（2）：431-437.LIU Guojing，HAN Xueshan，YANG Ming.Analysis and verification on three states between source and network in economic dispatch［J］.Power System Technology，2013，37（2）：431-437.

［16］WOLKOWICZ H，SAIGAL R，VANDENBERGHE L.Handbook of semidefinite programming：theory，algorithms，and applications［M］.New York，USA：Springer，2000：29-65.

［17］MADRIGAL M，QUINTANA V H.Semi-definite programming relaxations for ｛0，l｝ power dispatch problems［C］∥IEEE Power Engineering Society Summer Meeting，IEEE Conference Proceedings.Edmonton，Canada：［s.n.］，1999：697-702.

［18］白晓清，韦化.求解最优潮流问题的内点半定规划法［J］.中国电机工程学报，2008，28（19）：56-64.BAI Xiaoqing，WEI Hua.Solution of optimal power flow problems by semi-definite programming［J］.Proceedings of the CSEE，2008，28（19）：56-64.

［19］LAVAEI J，LOW S H.Zero duality gap in optimal power flow problem［J］.IEEE Trans on Power Systems，2012，27（1）：92-107.

［20］张宁宇，高山，赵欣.一种求解机组组合问题的内点半定规划GPU 并行算法［J］. 电力自动化设备，2013，33（7）：126-131.ZHANG Ningyu，GAO Shan，ZHAO Xin.GPU parallel algorithm of interior point SDP for unit commitment［J］.Electric Power Automation Equipment，2013，33（7）：126-131.

［21］王雅婷，何光宇，刘铠诚.求解状态估计问题的内点半定规划法［J］. 电网技术，2012，36（10）：209-215.WANG Yating，HE Guangyu，LIU Kaicheng.An semi-definite programming method for state estimation problem［J］.Power System Technology，2012，36（10）：209-215.

［22］ZHANG B，TSE D.Geometry of injection regions of power networks［J］.IEEE Trans on Power Systems，2013，28（2）：788-797.

［23］LESIEUTRE B C，MOLZAHN D K，BORDEN A R.Examining the limits of the application of semi-definite programming to power flow problems［C］∥49th Annual Allerton Conference on Communication，Control，and Computing，IEEE ConferenceProceedings.Monticello，IL，USA：［s.n.］，2011：1492-1499.

［24］MOLZAHN D K，LESIEUTRE B C，DEMARCO C L.A sufficient condition for global optimality of solutions to the optimal power flow problem［J］.IEEE Trans on Power Systems，2014，29（2）：978-979.

［25］田君杨.基于矩量理论的电力系统全局优化算法研究［D］.南宁：广西大学，2014.TIAN Junyang.Study on global optimization for power system based on theory of moment［D］.Nanning：Guangxi University，2014.

［26］LASSERRE J B.Global optimization with polynomials and the problem of moments［J］.SIAM Journal on Optimization，2001，11（3）：796-817.

［27］LASSERRE J B.A semidefinite programming approach to the generalized problem of moments［J］.Mathematical Programming，2008，112（1）：65-92.

［28］LASSERRE J B.Moments，positive polynomials and their applications［M］.London，UK：Imperial College Press，2009：15-102.

［29］SDPA.Available online［EB/OL］. （2014-12-20）［2014-12-26］.http：∥sdpa.indsys.chuo-u.ac.jp/sdpa/2010.

［30］李滨，韦化，李佩杰.电力系统无功优化的内点非线性互补约束算法［J］. 电力自动化设备，2010，30（2）：53-58.LI Bin，WEI Hua，LI Peijie.Interior-point nonlinear algorithm with complementarity constraints for reactive-power optimization［J］.Electric Power Automation Equipment，2010，30（2）：53-58.

［31］GÜLER T，GROSS G.Detection of island formation and identification ofcausalfactorsundermultiplelineoutages ［J］.IEEE Trans on Power Systems，2007，22（2）：505-513.

［32］KIM S，KOJIMA M，MEVISSEN M，et al.Exploiting sparsity in linearand nonlinearmatrix inequalitiesvia positive semidefinite matrix completion［J］.Mathematical Programming，2011，129（1）：33-68.

［33］西安交通大学.电力系统计算［M］.北京：水利电力出版社，1978：93-101.