基于节点重要度评价矩阵的网络重构双层优化策略

傅子昊 ，孙 磊 ，林振智 ，文福拴 ，2，朱炳铨 ，徐立中

（1.浙江大学 电气工程学院，浙江 杭州 310027；2.文莱科技大学 电机与电子工程系，文莱 斯里巴加湾 BE1410；3.国网浙江省电力公司，浙江 杭州 310007）

0 引言

近几年国内外发生了多起大面积停电事故，如 2003年“8·14”美加大停电、2005年中国海南电网“9·26”大停电事故、2006 年西欧互联电网“11·4”大停电事故以及2008年1月至2月中国南方部分省份电网受冰雪天气影响引起的停电事故等［1-3］，为电力系统的安全稳定运行敲响了警钟。一旦发生大面积停电，如果没有事先制定恢复预案，就会造成重大的经济损失。因此，有必要深入而系统地研究电力系统的事故处理及完全或部分停电后的系统恢复问题，这对减少故障影响和停电损失，确保事故发生后系统能安全、快速、智能地恢复供电，具有十分重要的理论和实际意义［4-6］。

大停电后的电力系统恢复可分为黑启动阶段、网络重构阶段和负荷恢复阶段。网络重构阶段的主要任务是尽快为失电机组送电并逐步建立起一个稳定的网架结构，为下一阶段全面恢复负荷打下坚实的基础［7-8］。近年来随着复杂网络理论研究的不断深入，由于电网具有的“小世界”效应，这方面的研究成果也被应用到网络重构的研究中。文献［9］采用节点收缩后的网络凝聚度来评价节点重要度，并基于此制定骨架网络重构策略，但该方法并未考虑线路的权重。文献［10］在文献［9］的基础上提出了一种综合考虑节点重要度和线路介数的网络重构策略，但当节点收缩后，与节点相连的带权重的线路也一并被收缩，从而导致收缩后的网络无法体现节点间的电气联系。文献［11］基于改进的节点收缩法制定网络重构策略，但该方法忽略了邻接节点对节点重要性的贡献以及节点间的依赖关系。文献［12］基于介数法提出了一种兼顾拓扑优先与路径电气影响的网络重构方法，但该方法只考虑了节点的全局重要性（位置信息），却忽略了节点的局部重要性（相邻节点信息）。

在上述背景下，本文基于相邻节点间重要度的贡献关系（即节点重要度评价矩阵）［13］提出了新的加权网络节点重要度的评价方法，并综合考虑了网络节点的位置和邻接节点的贡献信息；然后，在此基础上，针对文献［14］提出的网络重构两步策略没有考虑线路操作时间的弊端，发展了改进的网络重构双层优化模型，上层优化模型以最大化系统发电量为目标确定机组的最优启动时刻，下层优化模型以最大化恢复路径平均节点重要度为目标确定发电机节点的恢复路径，且通过调节系数改变线路权重中线路电容与操作时间的比重，以避免恢复路径所需的时间过长而延迟恢复待恢复的机组。

1 基于节点重要度评价矩阵的节点重要度评价方法

无权网络虽能反映网络的拓扑结构，但在电力网络中无法反映节点间的电气联系，而计及线路权值的加权电力系统拓扑模型在反映节点重要程度和实际电力系统运行状态等方面都优于无权模型［15］。本文对于线路权值的选取，一方面要考虑线路投运过程中的过电压风险，该风险可用线路电容表征；另一方面要尽可能减少线路恢复时间，尽量保证机组在热启动时限内启动。综合上述考虑，线路权值可由线路的充电电容和操作时间共同决定，即线路权值 wij= （1-v）Cij+vtij。 其中，wij为节点 vi和节点 vj之间线路的权值；Cij为节点vi和节点vj之间线路的充电电容；tij为节点vi和节点vj之间线路的操作时间（本文取值为恢复线路所需操作时间的期望值［16］）；v为调节系数，其选取方式将在下一节中详细阐述。

目前评价复杂网络节点重要度的经典方法有节点删除法、介数法、节点收缩法等，但这些方法都存在一定程度上的缺陷。对于节点删除法和介数法，它们都只考虑了节点的全局重要性（位置信息），而忽略了节点的局部重要性（相邻节点信息）。对于节点收缩法，一方面，如果某几个节点收缩后具有相同的拓扑结构，那这几个节点就具有相同的节点重要度；另一方面，当将该方法应用于加权网络［17］时，如果某节点与被收缩区域有多条线路相连，此时保留权值最小线路用于计算会导致这样的问题：假设某节点与被收缩区域有两条线路相连，则在互换这两条线路权值的情况下，该节点的节点重要度不会发生任何变化，这显然是不符合实际情况的。综上所述，现有方法没有考虑邻接节点对节点重要性的贡献，忽略了节点间的依赖关系，且大多都是基于无权网络提出的。在此背景下，本文提出了基于相邻节点间重要度的贡献关系（即节点重要度评价矩阵）［13］的加权网络节点重要度的评价方法，并综合考虑了节点自身在网络中所处位置（即全局重要性）及其相邻节点的重要度贡献（即局部重要性），使得节点评价更加准确。

1.1 理论基础

定义 1：加权图 G=｛V，E｝，其中，V=｛v1，v2，…，vn｝是网络中所有节点的集合，vi表示第i个节点，n为网络中节点的数目；E= ｛e1，e2，…，em｝代表节点间边的集合，且E⊆V×V，ei表示第i条边，m为网络中边的数目。 设邻接矩阵 W=［wij］n×n，其元素 wij的取值如下：若 vi和vj为相邻节点，则 wij等于 vi和 vj之间边的权值；若vi和vj为不相邻的节点，则wij=0；若i=j，则wij为无穷大。本文主要研究无向图，故wij=wji。

定义2：节点vk的效率Pk指该节点到网络中其他节点难易程度的平均值，即：

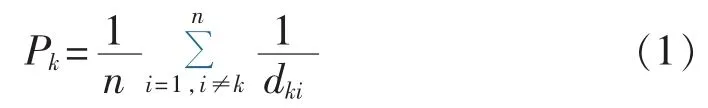
其中，n为网络中节点个数；dki为节点vi和节点vk之间权值总和最小的路径的总权值。

定义3：节点vi的点权Si定义为与节点vi直接相连的线路的权值和，即：

其中，ηi为与节点vi直接相连的节点的集合；wij为连接节点vi和节点vj的线路的权值。

1.2 节点重要度贡献矩阵

彼此孤立的节点之间原本并不存在重要度的依赖关系，但节点间一旦互相连接起来，节点的重要度就可能会发生变化。因此，互连节点的重要度相互影响/贡献，并与拓扑有关，该拓扑是实际网络拓扑的一个映射。本文用节点重要度贡献矩阵［13，18］来表示节点间这种重要度相互影响/贡献的拓扑关系。

定义4：节点重要度贡献矩阵。在n节点有权无向网络中，若节点vi的点权为Si，则vi将自身重要性的1/（wijSi）贡献给其相邻节点vj，将所有节点对其相邻节点的重要度贡献比例值用矩阵的形式表示出来，就形成了节点重要度贡献矩阵，记为 HI=［hij］n×n，其元素hij表示节点vj对节点 vi的重要度贡献比例值，并且取值如下：若 i=j，则 hij=1；若 i≠j，则 hij=1 /（wijSj）。 一方面，由点权的定义可以看出点权既考虑了节点的近邻数，也计及了节点与其邻接节点间的权重，这是节点局部信息的综合体现；另一方面，线路权值表征了2个节点间联系的紧密程度。 由 hij=1/（wijSj）可知，节点 vj与节点 vi间线路的权值越小，节点vj的点权Sj越小，则节点vj对节点vi的重要度贡献就越大。

1.3 节点重要度评价矩阵

由于节点的重要性取决于节点的位置信息和相邻信息。由定义2可以看出节点效率值越大，表明该节点在网络传输中所起的作用越大，故节点效率值可在一定程度上反映节点的位置信息。因此，将节点的效率值融合进节点重要度贡献矩阵HI，可得到节点重要度评价矩阵 HE=［qij］n×n，其元素 qij表示节点vj对节点vi的重要度贡献值且取值如下：若i=j，则qij=Pi；若 i≠j，则 qij=Pj/（wijSj）。 由 qij的定义可知，加权网络中某一节点对其相邻节点的重要度贡献值与自身的点权、效率值和与相邻节点间直接相连的线路的权值有关。节点效率用于表征一个节点到达网络中其他节点的难易程度，点权是节点局部信息的综合体现，线路权值用于表征2个节点间联系的紧密程度。 因此，由 qij=Pj/（wijSj）可知，节点 vj的效率 Pj越大，节点vj与节点vi间线路的权值越小，节点vj的点权Sj越小，则节点vj对节点vi的重要度贡献就越大。

运用节点重要度评价矩阵HE，综合考虑节点自身的效率和相邻节点的重要度贡献，可以定义节点i的重要度Ki为∶

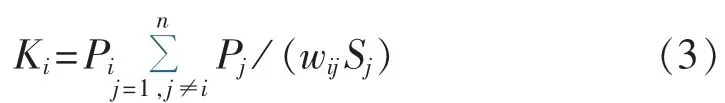
其中，Ki表示节点i所有的邻接节点对节点i的重要度贡献值之和与节点i自身效率的乘积。

2 网络重构的双层优化模型

确定机组的恢复顺序和优化恢复路径是网络重构需要解决的2个问题。本文在文献［14］提出的网络重构两步策略的基础上，提出了新的网络重构双层优化模型。在新的模型中，上层优化模型以最大化待恢复系统的发电量为目标，下层模型以最大化恢复路径的节点平均重要度为目标。本文主要改进之处为：针对文献［14］没有考虑线路操作时间的缺陷，定义了线路权值wij=（1-v）Cij+vtij，即其值由线路充电电容和操作时间共同决定，通过调整系数v即可调整线路权值中线路操作时间所占的比重，影响线路权值，进而改变节点重要度，最终决定了线路电容和线路操作时间这2个参数对恢复路径选择的影响程度。

2.1 确定非黑启动机组恢复顺序的上层优化模型

上层模型以最大化待恢复系统的发电量为目标，优化变量为非黑启动机组获得启动功率的时间，优化模型可表示为：

其中，［0，T］为所研究的时间区间；Nsnb为系统内非黑启动机组的数目；Pigen（t）为t时刻机组i的输出功率；Pistart为机组 i启动所需功率；ui（t）表示机组 i的恢复状态；Wtotal为研究时间区间内系统的发电量；ti，nes为机组i获得功率的时刻；ti，c为机组i启动所需时间；Ri为机组i的爬坡速率；Pi，max为机组i的最大输出功率。此外，在恢复过程中还应满足发电机出力约束、功率平衡约束、机组热启动和冷启动的时间约束等。

除上述约束条件之外，本文还须新增一个约束条件，即将上层优化模型求得的最优启动时刻代入到下层优化模型中，如果在机组i的恢复路径搜索的步骤中v=1，那么应把机组i通过该搜索路径获得启动功率的时刻回代到上层优化模型中，并作为机组i的最小启动时刻，即：

其中，ti，min为下层优化模型传递到上层优化模型中的值，即在下层优化模型计算中，如果机组i的恢复路径搜索步骤结束后v=1，则将启动功率通过v=1时的恢复路径送至机组i的时刻赋值给ti，min；否则，如果 v＜1，则 ti，min赋值为 0。

在上层优化模型的优化过程中，若当前已恢复的电源功率足以启动多个机组，则可采用并行恢复策略；否则，采用串行恢复策略依次恢复相关机组。

2.2 确定恢复路径的下层优化模型

在上层优化模型确定了机组的启动时刻之后，下层模型以最大化恢复路径的节点平均重要度为目标来选择发电机节点的恢复路径。恢复路径的节点平均重要度定义如下：

其中，Γ为恢复路径所经过的未恢复供电的节点集合；Ki为节点i的重要度；NΓ为恢复路径所经过的未恢复供电的节点数目。

可供选择的恢复路径是从已恢复的带电区域到待恢复机组之间的恢复路径。确定恢复路径的优化目标为：

式（9）为恢复路径寻优的目标函数，即从带电区域到待恢复机组的路径中选择节点平均重要度最大的路径作为恢复路径。每恢复一条线路，就将该线路及其两端节点合并到带电区域中。

在恢复路径寻优过程中，还需注意所选择路径必须是非冗余路径。如果一条路径中含有2个或2个以上已充电节点（包括起始节点），则该条路径即为冗余路径。

为避免恢复路径所需的时间过长而延迟恢复待恢复的机组，本文在计算节点重要度时不仅考虑了线路电容的影响，还考虑了线路操作时间的影响。

对于线路权值 wij=（1-v）Cij+vtij，在初始状态下取v=0，此时线路权值完全由线路电容决定。当把上层优化模型求得的机组恢复顺序代入到下层优化模型中并求得恢复路径之后，若待恢复机组i获得启动功率的时间大于上层优化模型计算出的机组i的启动时刻ti，nes，则逐步增大v的值得到新的线路权值，然后重新以最大化节点平均重要度为目标搜索机组i的恢复路径，直至满足i获得启动功率的时间不大于ti，nes或v=1为止。当v=1时，线路权值完全由操作时间决定，则优化结果为线路操作时间最短的恢复路径。

3 求解方法与步骤

本文采用改进的粒子群算法［19］来求解改进的网络重构双层优化模型，求解步骤如下。

步骤1：输入粒子群算法的初始参数，包括种群规模M、学习因子c1和c2、惯性权重ω和粒子群繁殖代数Mc。

步骤2：随机生成M个待恢复机组的启动顺序，以此作为初始粒子群。

步骤3：针对每一个粒子，调用双层优化模型，求解上层模型得到机组的启动时刻并计算出系统的发电量，再求解下层模型得到发电机节点的恢复路径，从而得到每个粒子的目标函数值。

步骤4：根据目标函数值计算各个粒子的适应度，该适应度定义为系统发电量。

步骤5：更新粒子的位置和速度，得到新的粒子。

步骤6：重复步骤3—5，直到达到粒子群繁殖代数Mc。

步骤7：选出最优粒子，其对应的上层模型的解即为最优的机组启动时刻，下层模型的解即为恢复路径。

4 算例与分析

以新英格兰10机39节点系统［14］为例来说明本文所提出的方法。假设节点33为黑启动机组所在节点，节点 30、31、32、34、35、36、37、38、39 为待恢复的发电机所在节点，且每个发电节点只有一台发电机组。各线路参数和发电机组参数可参见文献［14］。给定粒子群种群规模M=20，粒子群繁殖规模Mc=50，学习因子c1、c2和惯性权重ω按文献［19］所述方法确定初值并动态调整。

采用改进的粒子群算法求解网络重构的双层优化问题，得到发电机节点恢复时刻的最终优化结果如下（括号中为机组相应的恢复时刻）：33（0 min）、34（10 min）、30（17 min）、37（26 min）、36（37 min）、35（44 min）、32 （49 min）、38 （55 min）、31 （70 min）、39（70 min）。发电机组恢复时刻的计算采用了文献［20］所述的方法，这里不再赘述。

为验证本文方法的有效性，将本文方法与文献［14］方法进行比较，对比结果如表1所示。由表1可以看出，本文方法与文献［14］方法的差别主要体现在对节点30所在机组恢复路径的选择上。采用文献［14］的恢复路径，到第55 min时系统的机组输出功率为36MW，而节点38所在机组启动所需功率为37 MW，此时系统提供的功率不足以启动该机组，而该发电机的最大热启动时限为55 min，所以在文献［14］的恢复路径下，该机组无法在最大热启动时限内进行热启动，只能在几小时后选择冷启动；而由于节点38所在机组无法热启动，导致后续待恢复的机组进一步推迟恢复。采用本文方法得到的恢复路径进行机组的恢复，则第55 min时系统提供的功率为41.4 MW，大于节点38所在机组启动所需的功率，所以该机组能够在热启动时限内热启动。

表1 2种方法求得的各发电节点恢复路径Table 1 Generator node restoration paths by two methods

最后对研究时段终点的机组输出功率和发电量进行比较，对比结果如图1所示。

由图1可以看出，在第180 min时，采用本文方法和文献［14］的方法所得到的机组输出功率分别为2091 MW和1935 MW，研究时间段内的发电量分别为1650 MW·h和1604 MW·h，可见采用本文方法可以更快地实现电力系统的恢复。

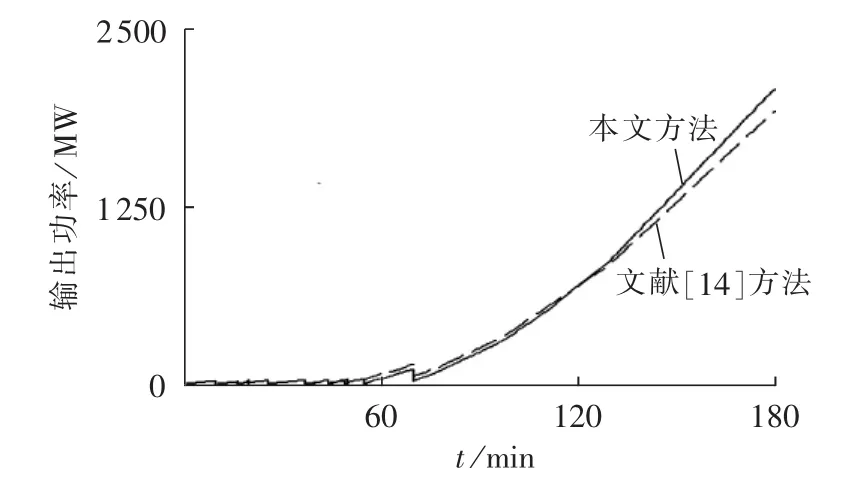
图1 采用2种方法得到的机组输出功率Fig.1 Unit output power curves by two methods

5 结语

本文首先提出了利用节点重要度评价矩阵评价加权网络节点重要度的方法，该方法对节点的评价更加全面。之后发展了一种基于该节点重要度评价方法的改进的网络重构双层优化模型。在该双层优化模型中，上层优化模型以非黑启动机组获得启动功率的时间为优化变量，并以最大化系统发电量为目标；下层优化模型以最大化恢复路径平均节点重要度为目标确定发电机节点的恢复路径，并将可调节线路电容和线路操作时间所占比重的线路权值引入到节点重要度评价中，有效避免了在系统有足够功率启动某台机组时却由于恢复路径所需时间过长导致该机组延迟恢复的情况发生。算例结果表明了所提出的方法的基本特征，为大停电后的系统恢复提供了新的思路。值得指出的是，实际上系统恢复过程是一个动态过程，部分节点恢复后会对剩余节点重要度产生影响，研究节点数量发生变化后的动态网络节点重要度计算方法，以得到更为准确的网络重构策略是下一步值得研究的问题。

［1］ANDERSSON G，DONALEK P，FARMER R，et al.Causes of the 2003 major grid blackouts in North America and Europe，and recommended means to improve system dynamic performance［J］.IEEE Transactions on Power Systems，2005，20（4）：1922-1928.

［2］唐斯庆，张弥，李建设，等.海南电网“9·26”大面积停电事故的分析与总结［J］. 电力系统自动化，2006，30（1）：1-7，16.TANG Siqing，ZHANG Mi，LI Jianshe，et al.Review of blackout in Hainan on September 26th-causes and recommendations［J］.Automation of Electric Power Systems，2006，30（1）：1-7，16.

［3］刘有飞，蔡斌，吴素农.电网冰灾事故应急处理及反思［J］.电力系统自动化，2008，32（8）：10-13.LIU Youfei，CAI Bin，WU Sunong.Emergency management for the ice disaster in power grids and some suggestions［J］.Automation of Electric Power Systems，2008，32（8）：10-13.

［4］孙磊，张璨，林振智，等.大停电后电力系统黑启动分区的两步策略［J］. 电力自动化设备，2015，35（9）：14-21.SUN Lei，ZHANG Can，LIN Zhenzhi，et al.Two-step strategy for black-start zone partitioning of power system after blackout［J］.Electric Power Automation Equipment，2015，35（9）：14-21.

［5］梁博淼，林振智，文福拴，等.发电机组并行恢复动态决策的熵权方法［J］. 电力自动化设备，2015，35（5）：119-125，159.LIANG Bomiao，LIN Zhenzhi，WEN Fushuan，et al.Dynamic strategy based on entropy weight theory for parallel restoration of generators［J］.Electric Power Automation Equipment，2015，35（5）：119-125，159.

［6］李从善，刘天琪，李兴源.停电应急预案快速匹配与智能生成方法［J］. 电力自动化设备，2014，34（1）：32-36，42.LI Congshan，LIU Tianqi，LI Xingyuan.Fast matching of power outage event and intelligent generation of power recovery plan［J］.Electric Power Automation Equipment，2014，34（1）：32-36，42.

［7］陈亮，顾雪平，贾京华.考虑后续恢复影响的扩展黑启动方案多目标优化与决策［J］. 电力自动化设备，2014，34（2）：137-143，150.CHEN Liang，GU Xueping，JIA Jinghua.Multi-objective optimization and decision making of extended black-start scheme considering subsequent restoration influence［J］.Electric Power Automation Equipment，2014，34（2）：137-143，150.

［8］杨可，刘俊勇，贺星棋，等.黑启动中考虑动态过程的负荷最优恢复［J］. 电力自动化设备，2009，29（10）：88-92.YANG Ke，LIU Junyong，HE Xingqi，et al.Optimal load restoration considering dynamic constraints during black-start［J］.Electric Power Automation Equipment，2009，29（10）：88-92.

［9］LIU Y，GU X P.Skeleton-network reconfiguration based on topological characteristics of scale-free networks and discrete particle swarm optimization［J］.IEEE Transactions on Power Systems，2007，22（3）：1267-1274.

［10］王亮，刘艳，顾雪平，等.综合考虑节点重要度和线路介数的网络重构［J］. 电力系统自动化，2010，34（12）：29-33.WANG Liang，LIU Yan，GU Xueping，et al.Skeleton-network reconfiguration based on node importance and line betweenness［J］.Automation of Electric Power Systems，2010，34（12）：29-33.

［11］杨丽君.电力系统大停电后恢复算法研究［D］.秦皇岛：燕山大学，2010.YANG Lijun.Research on restoration algorithms in power system after wide area blackout［D］.Qinhuangdao：Yanshan University，2010.

［12］张国松，刘俊勇，魏震波，等.兼顾拓扑优先与路径电气影响的骨架网络重构［J］. 电力系统保护与控制，2011，39（17）：1-6.ZHANG Guosong，LIU Junyong，WEIZhenbo，etal.Skeletonnetwork reconfiguration based on topology priority and path electrical effects［J］.Power System Protection and Control，2011，39（17）：1-6.

［13］姜志鹏，张多林，马婧，等.权重演化的加权网络节点重要性评估方法［J］.空军工程大学学报（自然科学版），2015，16（2）：19-23.JIANG Zhipeng，ZHANG Duolin，MA Jing，et al.Research on evaluation method for node importance based on weighted-evolution network mode［J］.Journal of Air Force Engineering University（Natural Science Edition），2015，16（2）：19-23.

［14］张璨，林振智，文福拴，等.基于后悔思想的网络重构两步策略［J］. 电力系统自动化，2013，37（8）：46-52，75.ZHANG Can，LIN Zhenzhi，WEN Fushuan，et al.A two-stage strategy for network reconfiguration based on the concept of regret［J］.Automation of Electric Power Systems，2013，37（8）：46-52，75.

［15］丁明，韩平平.加权拓扑模型下的小世界电网脆弱性评估［J］.中国电机工程学报，2008，28（10）：20-25.DING Ming，HAN Pingping.Vulnerability assessment to smallworld power grid based on weighted topological model［J］.Proceedings of the CSEE，2008，28（10）：20-25.

［16］曾顺奇，文福拴，薛禹胜，等.计及操作时间不确定性的电力系统网络重构优化策略［J］. 电力系统自动化，2011，35（23）：16-20.ZENG Shunqi，WEN Fushuan，XUE Yusheng，et al.Optimization ofnetwork reconfiguration strategy forpowersystems considering operating time uncertainty［J］.Automation of Electric Power Systems，2011，35（23）：16-20.

［17］朱涛，张水平，郭戎潇，等.改进的加权复杂网络节点重要度评估的收缩方法［J］.系统工程与电子技术，2009，31（8）：1902-1905.ZHU Tao，ZHANG Shuiping，GUO Rongxiao，et al.Improved evaluation method for node importance based on node contraction in weighted complex networks［J］.Systems Engineering and Electronics，2009，31（8）：1902-1905.

［18］周漩，张凤鸣，李克武，等.利用重要度评价矩阵确定复杂网络关键节点［J］. 物理学报，2012，61（5）：050201.1-050201.7.ZHOU Xuan，ZHANG Fengming，LI Kewu，et al.Finding vital node by node importance evaluation matrix in complex networks［J］.Acta Physica Sinica，2012，61（5）：050201.1-050201.7.

［19］卢志刚，董玉香.基于改进二进制粒子群算法的配电网故障恢复［J］. 电力系统自动化，2006，30（24）：39-43.LU Zhigang，DONG Yuxiang.Distribution system restoration based on improved binary particle swarm optimization［J］.Automation of Electric Power Systems，2006，30（24）：39-43.

［20］LIU C C，LIOU K L，CHU R F，et al.Generation capability dispatch for bulk power system restoration：a knowledge-based approach［J］.IEEE Transactions on Power Systems，1993，8（1）：316-325.