含VSC-MTDC的交直流混合电网潮流计算模型及稀疏性处理技术

鲍 威 ，凌卫家 ，张 静 ，王 栋 ，张 磊 ，田 晖 ，郭瑞鹏

（1.浙江大学 电气工程学院，浙江 杭州 310027；2.国网浙江省电力公司，浙江 杭州 310007；3.国网舟山供电公司，浙江 舟山 316021）

0 引言

柔性直流输电（VSC-HVDC）技术使用电压源换流器（VSC）替代传统的整流器与逆变器，具有双向可控、换相不依赖电网过零、谐波水平低［1］、无功有功独立调节［2］、可向无源网络供电［3-4］等特点，其灵活的控制方式和理想的运行特性在解决大规模可再生能源并网、大容量远距离电能输送、输电走廊紧缺等问题时有着较大的技术优势［5］。随着可再生能源的不断发展，我国大规模新能源系统并网问题日益突出，多端直流输电（MTDC）系统拓扑在电网建设经济上的优势逐渐显现［6-8］，而VSC-HVDC技术的发展为MTDC系统的实现提供了条件。多端柔性直流（VSCMTDC）因其能够实现多电源供电、多落点受电的特点，为我国分散的可再生能源提供了一种更为灵活、快捷、经济的输电方式［9-10］。随着全控型器件生产技术的不断成熟，其制作成本明显降低，且器件容量以及耐压能力显著提高，VSC-HVDC的需求及应用呈现出上升态势。在此背景下，对于VSC-HVDC的运行、控制等方面的研究也受到越来越多的关注。

潮流计算是电力系统分析的根本，然而对于含VSC-MTDC的电力系统，传统的潮流计算已不再适用。因此，自HVDC技术面世以来，许多的学者与研究人员投身于交直流混合电网潮流计算的研究。目前，传统交直流混合系统的潮流计算方法已比较成熟，但仍然缺少一种成熟的含VSC-MTDC的交直流混合系统统一潮流计算算法。由于VSC-MTDC独特的网络拓扑使得其在控制策略上与两端VSC-HVDC及传统HVDC有着较大区别，VSC-MTDC的控制策略一直是学者研究的热点之一［6，11-15］。在进行含VSCMTDC交直流混合系统潮流计算建模时，需要构建不同的控制方程来对应不同的控制策略，而这些控制方程的引入，可能会破坏潮流雅可比矩阵的结构对称性及对角占优性而导致潮流计算求解失败。因此，对于潮流稀疏矩阵的处理也是含VSC-MTDC的交直流混合系统潮流计算算法的重点之一。

文献［16］使用交替法进行潮流计算求解，但忽略了VSC的有功损耗，且对控制策略的讨论较少，因此不具有一般性。文献［17］仅讨论了双端VSC-HVDC的一种控制策略，且未讨论潮流计算求解的难点，较难实用化。文献［18-22］考虑了双端VSC-HVDC的4种控制策略，但都未考虑VSC-MTDC的控制策略组合，其中文献［18］将自动微分技术应用到最优潮流算法中；文献［19］使用了一种基于差分进化和原-对偶内点法的混合算法；文献［20］则比较了原-对偶内点法与预测-校正内点法在含VSC-HVDC系统最优潮流计算中的优劣；文献［21］使用了交替法进行潮流计算求解，该方法可以规避潮流雅可比矩阵结构不对称及零对角元的问题，但由于模型不是统一模型，可扩展性较差；文献［22］使用了统一求解模型，但未考虑到含VSC-MTDC系统潮流雅可比矩阵可能出现的结构不对称及零对角元情况，算法的效率和收敛可靠性都有待检验。

本文给出了一种含VSC-MTDC的交直流混合电网的潮流计算统一模型，根据VSC的电气特性推导出统一的节点功率方程，并提出了9种不同VSC控制模式的等效数学方程。由于含VSC的潮流雅可比矩阵可能不具有结构对称性和对角元占优性，本文提出了几种稀疏性处理方法，恢复了雅可比矩阵的结构对称性，并保证了三角分解时不会遇到零主元。经含VSC-MTDC的实际交直流混合电网验证了本文方法的正确性与实用性。

1 交直流混合电网的元件稳态等值模型

1.1 VSC模型

VSC是VSC-MTDC系统的关键元件，是直流系统与交流系统之间联系的纽带。各VSC一侧连接于直流网络，另一侧连接于交流网络，是直流网络与交流网络功率交换的桥梁。

本文将实际VSC等值为理想电压源换流串联等值阻抗，记电网中的第k个VSC为VSCk，相关物理量以及其参考方向如图1所示。图1中，ak、dk分别表示VSCk直流侧和交流侧节点的节点编号；Rk、Xk分别表示VSCk的等值电阻及等值电抗；Uck∠θck、Uak∠θak、Udk分别表示 VSCk的等值内电势相量、交流侧电压相量及直流侧电压幅值；Pak、Qak、Pdk分别表示VSCk的交流侧有功、无功及直流侧有功。

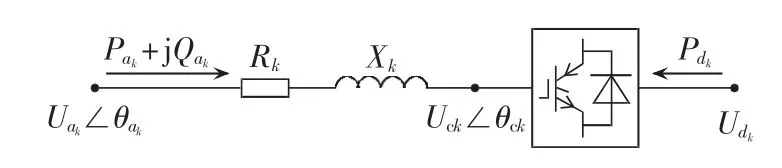
图1 电压源换流器等值电路Fig．1 Equivalent circuit of VSC

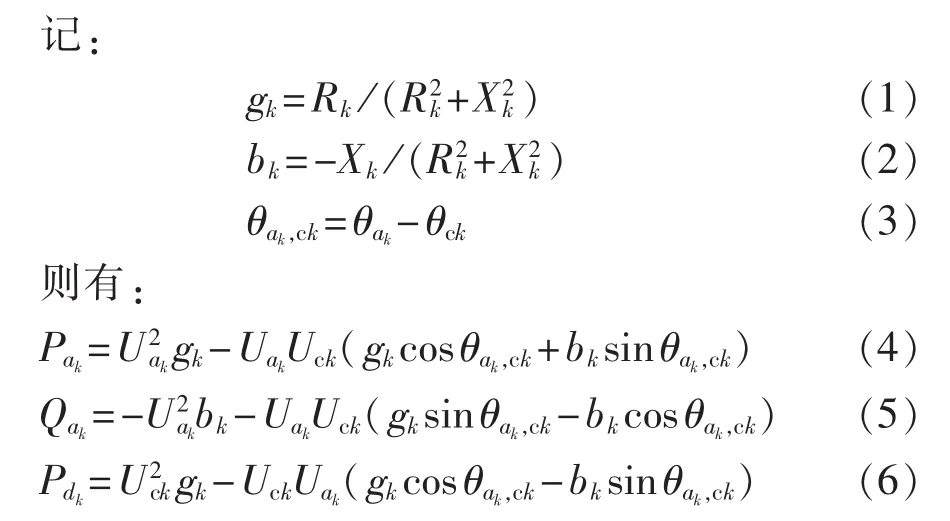
1.2 直流线路模型

对于电网中第g条直流线路，设其始、末端节点号分别为 i、j，相关物理量及其参考方向见图2。直流线路的模型公式不再赘述。

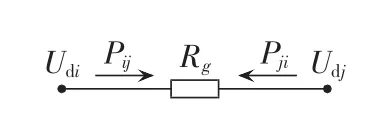
图2 直流线路等值电路Fig．2 Equivalent circuit of DC line

2 潮流计算模型

状态量定义是潮流计算的基础，本文的交直流混合系统潮流计算模型对于交流节点，取电压幅值及相位作为状态量；对于直流节点，取电压幅值作为状态量；对于VSC，取等值电源内电势幅值及相位作为状态量。对于含MTDC的交直流混合系统，若PQ节点数为NPQ，PV节点数为NPV，直流节点数为NDC，VSC数为NVSC，且VSC控制目标均以控制方程的方式引入（而非将某一状态量处理为常量），则状态量的数量为2NPQ+NPV+NDC+2NVSC。从建模对象方面，该潮流计算模型主要包括3类方程：交流节点的有功及无功潮流平衡方程；直流节点的有功潮流平衡方程；与机组或VSC控制模式各类设定值对应的方程。其中，NPQ个交流节点电压幅值状态量对应于相应交流节点的无功潮流平衡方程；NPQ+NPV个交流节点电压相位状态量对应于相应交流节点的有功潮流平衡方程；NDC个直流节点电压幅值状态量对应于相应直流节点的有功潮流平衡方程；NVSC个VSC等值电源内电势相位状态量对应于相应VSC的有功类控制方程，NVSC个VSC等值电源内电势幅值状态量对应于相应VSC的无功类控制方程；VSC的交流节点及换流变并网节点的状态量也可能涉及于某些控制方程中。

2.1 交流节点的有功及无功潮流平衡方程

交直流混合系统中的交流节点可分为2类。若某交流节点为VSC元件的交流侧节点，则称为混合交流节点，反之则称为传统交流节点。对于传统交流节点，其功率方程即传统潮流计算节点功率平衡方程；而对于混合交流节点，则需要考虑VSC的模型特性。因此，引入以下数学概念辅助建立统一的潮流平衡方程：令为与节点i相邻的传统交流节点编号集；令为与节点i相邻的VSC编号集，若节点i不是任一VSC的交流侧或直流侧节点，则为空集。则交直流混合系统中交流节点潮流平衡方程如下：

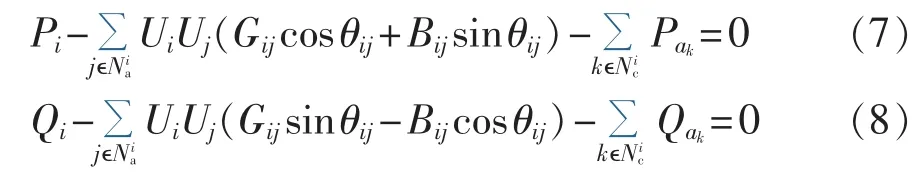
其中，Gij及Bij分别表示节点导纳矩阵第i行第j列元素的实部及虚部；θij表示节点i与节点j之间的相位差；Pi及Qi分别表示节点i的有功及无功注入功率；Ui及Uj分别表示节点i及节点j的电压幅值。

2.2 直流节点的有功潮流平衡方程

考虑到直流电源，将直流节点也类似地分为2类。若某直流节点为VSC元件的直流侧节点，则称为混合直流节点，反之则称为传统直流节点。同样引入数学概念辅助建立统一的潮流平衡方程：令Nid为与节点i相连的直流节点编号集。交直流混合系统的直流节点潮流平衡方程如下：

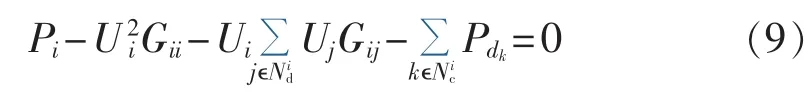
2.3 控制设定值方程

交直流混合系统潮流计算中的控制设定值方程主要可分为2类，其中平衡机及PV节点的控制方程与传统潮流计算一样，不再赘述。下面主要介绍VSC元件的控制方程。

2.3.1 VSC有功类控制方程

VSC有功类控制目标主要有5类，控制方程如下。

（1）定直流电压控制方程。

（2）定换流器直流有功控制。

（3）定换流器交流有功控制。

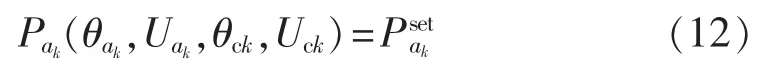
（4）定换流变并网有功控制。

VSC一般通过换流变接入交流电网，结构见图3。

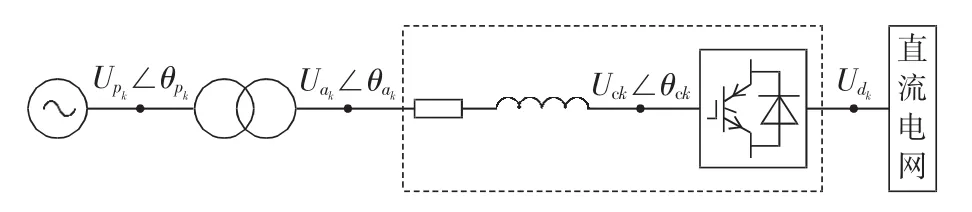
图3 带换流变的电压源换流器等值电路Fig．3 Equivalent circuit of VSC with transformer

则定并网点功率控制方程为：

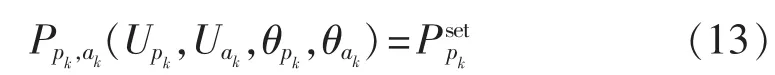
其中，pk表示 VSCk的并网侧节点编号，Upk、θpk分别表示该节点的电压幅值与相位。

（5）向孤岛供电的定频率控制。

VSC向交流孤岛供电时，实际上充当了孤岛平衡电源的角色，故需为孤岛内的电压选择相位参考点。本文直接选择换流器内电势相位作为参考点，即：

2.3.2 VSC无功控制方程

VSC无功类控制目标主要有4类，控制方程如下。

（1）定换流器交流电压控制。

（2）定并网点电压控制。

（3）定换流器无功控制。

（4）定换流变并网无功控制。

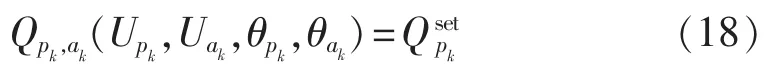
显然，交流节点的有功潮流平衡方程对应于相应的电压相位状态量，交流节点的无功潮流平衡方程对应于相应的电压幅值状态量，直流节点的有功潮流平衡方程对应于相应的直流电压状态量。对于VSC，有功类控制目标约束方程对应于内电势相位，无功类控制目标约束方程对应于内电势幅值。

2.4 平衡节点的选取

首先讨论对直流系统平衡节点的选取。对于任一MTDC系统，必须且只能选择一个VSC采用定直流电压控制，采用定直流电压控制的VSC事实上充当着该直流系统平衡电源的角色，其各侧的有功功率在潮流计算收敛前是未知的，这就要求其所连接的交流系统拥有平衡电源。理论上，只要VSC所连接的交流系统有平衡电源，即可将其设为定直流电压控制模式，实用中通常选择其中容量最大的VSC采用定直流电压控制模式。因此，定直流电压控制模式VSC的直流侧节点即为相应MTDC系统的电压参考节点，参考节点电压的大小可以由用户设定。实用中，由于直流系统一般不考虑升压或降压运行，故参考节点电压一般直接设为1.0 p.u.。

下面讨论交流系统平衡节点的选取。MTDC系统向一个有源交流系统供电时可能存在2种情况。一种情况是该有源交流系统没有平衡机（即各电源的有功控制均采用定功率控制模式，如处理为PV或PQ节点），MTDC连接该交流系统侧VSC采用定频率控制模式。这种情况的本质是以MTDC作为该交流系统的平衡电源，但理论上可取交流系统任一节点作为相位参考点，也可取相应VSC等值电源内电势相位作为相位参考点，本文取VSC内电势相位作为相位参考点。另一种情况则是交流系统本身有平衡机，MTDC连接该交流系统侧换流阀采用除定频率控制模式之外的有功控制模式（如定并网点有功控制模式、定阀交流侧有功控制模式、定阀直流侧有功控制模式或定直流电压控制模式），该情况下选择该平衡机所在节点作为相位参考点。

3 含VSC的潮流计算稀疏矩阵处理技术

在传统交流潮流计算中，由于节点有功潮流平衡与节点电压相位关系密切，节点无功潮流平衡方程与节点电压幅值关系密切。取节点有功潮流平衡方程的行号作为相应节点电压相位的变量号，取节点无功潮流平衡方程的行号作为相应节点电压幅值的变量号，则潮流雅可比矩阵具有结构对称性及对角占优性两大特点，这事实上是电力系统潮流计算采用节点编号优化进行稀疏矩阵处理的理论基础。

对于含VSC的交直流混合电网，除了交流节点之外，还有直流节点，相应地有节点有功潮流平衡方程，而直流节点的状态量则为直流电压幅值。由于直流节点的功率平衡方程与直流节点的电压幅值关系密切，故可以取有功潮流平衡方程的行号作为相应节点直流电压幅值的变量号，其对角元素值非零，且一般具有对角占优性。

对于VSC，将有功类控制方程的行号作为等值电源内电势相位的变量号，将无功类控制方程的行号作为等值电源内电势幅值的变量号。然而，VSC控制方程与具体的控制模式有关，潮流雅可比矩阵与VSC对应的行及列间一般不具有结构对称性。此外，有功类控制方程不一定与等值电源内电势相位有直接关系，无功类控制方程也不一定与等值电源内电势幅值有直接关系，即潮流雅可比矩阵与VSC控制方程对应的对角元素值可能为零。VSC的引入增广了潮流修正方程，使得潮流雅可比矩阵不再具有结构对称性和对角占优性，且对角元素可能为零，难以直接采用传统的纯交流系统潮流计算的稀疏矩阵技术。

3.1 非结构对称性的处理

对于不具有结构对称性的潮流雅可比矩阵，最直接的处理办法便是将其直接视为非结构对称矩阵处理，采用选主元或部分选主元的方法进行三角分解。但由于潮流雅可比矩阵不是常数矩阵，每次迭代时都需重新进行三角分解，因而需要付出高昂的计算代价，在实用中不可取。

本文使用了一个简单的规则来解决这个问题：当潮流雅可比矩阵的i行、j列为非零元素时，则认为j行、i列也为非零元素（即使其实际数值可能为零）。由于VSC扩展行及扩展列的稀疏性均很好，且有部分非零元素本身就是结构对称的，该规则引入的附加非零元素数量是微不足道的。

3.2 零对角元素的处理

对于VSC扩展行及扩展列中可能出现的零对角元素问题，若在稀疏矩阵处理上不加特殊处理，潮流雅可比矩阵三角分解时可能遇到零对角元，将直接导致潮流计算失败。一种简单的处理方法是在三角分解遇到零对角元时将其替换为某一较小正值ε，使潮流雅可比矩阵的三角分解过程能够正常进行。替换法存在一定的隐患，可能会存在潜在的数值问题：ε取得过小，可能因潮流雅可比矩阵左上角部分子矩阵的严重病态而导致潮流计算不收敛或收敛速度变慢；ε取得过大，可能因潮流雅可比矩阵的偏差导致潮流计算的收敛性变差。此外，替换法在潮流雅可比矩阵引入了偏差项，可能影响基于潮流雅可比矩阵的灵敏度分析结果。本文在节点编号优化中引入限制条件，使潮流雅可比矩阵三角分解时不遇到零对角元素，从而避免在潮流雅可比矩阵中引入偏差项，克服潮流雅可比矩阵零对角元素可能给潮流计算带来的数值困难，提高潮流计算的收敛速度。下面按VSC的不同控制模式讨论节点编号优化方法。

3.2.1 不需特殊处理的控制模式

对于向孤岛供电的定频率控制模式，由式（14）可以发现，直接取VSC内电势作为相位参考点时，其对角元非零，故不需进行特殊处理。

对于定换流器交流有功、定换流器交流无功与定直流有功控制，由于控制目标方程（11）、（12）及（17）都与VSC内电势状态有关，其对角元非零，也不需进行特殊处理。

3.2.2 常量替代法

对于定直流电压控制模式，观察控制目标方程（10）可以发现，只要将Udk当成状态变量，并保证直流电压的变量编号位于VSCk内电势相位θck编号之前，即可保证不出现零对角元。但为了尽量减少变量编号的调整，本文方法将Udk直接替换为常量Usetdk代入方程，并将该直流节点的有功潮流平衡方程作为控制模式对应方程，由于直流节点的有功平衡方程与VSC内电势相位有关，故可保证对角元非零。

3.2.3 优先排序法

对于定换流器交流电压、定并网点电压、定换流变并网有功与定换流变并网无功控制模式，由于控制目标方程（13）、（15）、（16）及（18）都与 VSC 内电势状态无关，故控制模式对应的雅可比矩阵对角元素为零，由于控制目标方程的稀疏性较好，如果不进行特殊处理，其行编号在稀疏性结构优化时将排在较为靠前的位置，三角分解时可能出现零对角元的情况，导致潮流计算失败。因此，在进行变量编号时，将VSC控制模式相关变量优先进行编号，保证其编号位于内电势相应变量编号之前。

假设VSCk采用定并网点有功及无功控制模式，则其交流侧相关部分的稀疏矩阵结构如下：

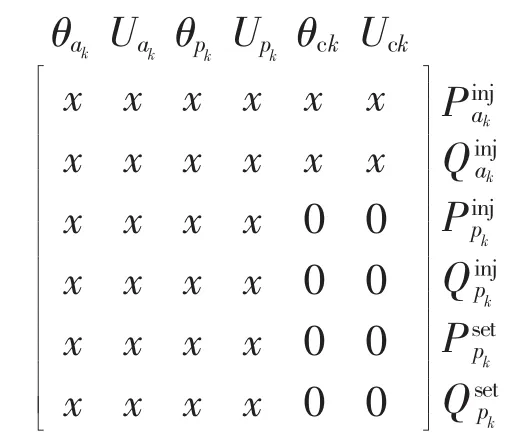
其中，x表示非零元素。可见，只需保证变量θak位于变量θck之前，变量 Uak位于变量Uck之前，即可保证三角分解过程不遇到零对角元。

假设VSCk采用定并网点有功及电压控制模式，则其交流侧相关部分的稀疏矩阵结构如下：

可见，只需保证变量θak位于变量θck之前，变量及位于变量Uck之前，即可保证三角分解过程不遇到零对角元。

假设VSCk采用定交流侧有功及电压控制模式，则其交流侧相关部分的稀疏矩阵结构如下：

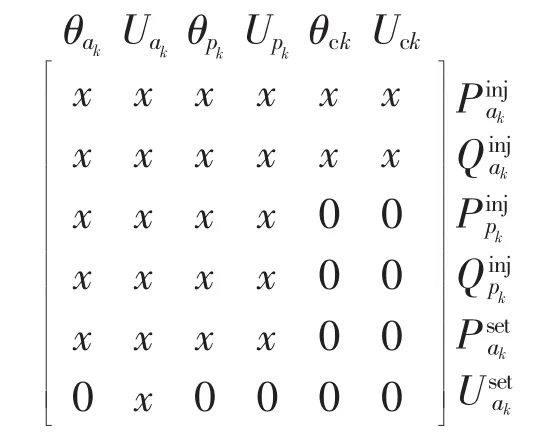
可见，只需保证变量θak位于变量θck之前，变量Uak位于变量Uck之前，即可保证三角分解过程不遇到零对角元。

由于VSC交流侧节点及并网点一般均具有很好的稀疏性（节点的度一般为2），优先排序法可能引入的附加非零注入元素数量非常有限。当然，对于定换流器交流电压控制，也可以使用常量替代法，将交流侧无功潮流平衡方程处理为控制模式方程，由于交流侧无功潮流平衡方程与内电势相关，故对角元非零。对于实际电网，由于VSC的数量较为有限，以上不同处理方法执行进度的差异非常小，因此在选择方法时无需考虑对计算机性能的影响。

4 算例分析

采用本文方法对含舟山五端VSC-HVDC的浙江电网某运行方式进行了仿真计算，电网的计算规模如下：交流节点数为6031，交流支路数为8587，直流节点数为5，直流线路数为5，VSC数为5。

采用半动态法优化变量编号，表1为不同有功及无功控制模式下潮流计算雅可比矩阵的稀疏性信息。表中非零元数量及非零注入元数量指雅可比矩阵的上三角部分，不包括下三角部分及对角部分。可见，限定变量编号顺序对非零注入元数量的影响很小，表中第2、3行算例，非零注入元数量不增反减。

表1 各控制模式潮流雅可比矩阵的稀疏性比较Table1 Comparison of Jacobi matrix sparsity among different control modes

此外，对于表1各算例，潮流计算迭代次数均为5次，所花费的CPU时间均约为34 ms（仅指创建导纳矩阵、创建并优化雅可比矩阵稀疏性、算法启动、迭代计算及支路潮流计算等花费的时间，不包括数据文件解析、网络拓扑分析及潮流计算结果保存等花费的时间）。这是由于算例中的非零注入元数量变化很小，不同控制模式之间的单次迭代计算性能差别也很小，说明本文算法对电网方式中VSC的不同控制模式都具有良好的效果。

5 结论

本文推导了VSC目前常见的9种控制模式的潮流约束方程，基于极坐标牛顿-拉夫逊法，提出了一种统一的含VSC-MTDC交直流混合电网潮流计算模型。进而针对VSC元件可能引起的潮流雅可比矩阵的非结构对称性及零对角元问题，给出了相应的稀疏矩阵处理技术。实际电网的仿真结果验证了所提方法的正确性及效率。

本文算法是一种实用性极强的成熟算法，可直接对含VSC-MTDC的大规模实际电网进行潮流计算。本文使用了一个理想电阻等效表示换流器的有功损耗，下一步研究考虑使用百分比来表示有功损耗，以更贴近电网实际。

［1］张凯，李庚银，梁海峰，等.基于电压源换流器HVDC系统稳态控制及仿真［J］. 电力自动化设备，2005，25（3）：79-82.ZHANG Kai，LIGengyin，LIANG Haifeng，etal.Steady-state control strategy and simulation of VSC-HVDC［J］.Electric Power Automation Equipment，2005，25（3）：79-82.

［2］陈谦，唐国庆，胡铭，等.采用dq0坐标的VSC-HVDC稳态模型与控制器设计［J］. 电力系统自动化，2004，28（16）：61-66.CHEN Qian，TANG Guoqing，HU Ming，et al.Steady-state model and controller design of a VSC-HVDC converter based on dq0-axis［J］.Automation of Electric Power Systems，2004，28（16）：61-66.

［3］梁海峰，李庚银，李广凯，等.向无源网络供电的VSC-HVDC系统仿真研究［J］. 电网技术，2005，29（8）：45-50.LIANG Haifeng，LI Gengyin，LI Guangkai，et al.Simulation study of VSC-HVDC system connected to passive network［J］.Power System Technology，2005，29（8）：45-50.

［4］邹超，王奔，李泰.向无源网络供电的VSC-HVDC系统控制策略［J］. 电网技术，2009，33（2）：84-88，110.ZOU Chao，WANG Ben，LI Tai.Control strategy of VSC-HVDC system supplying power for passive networks［J］.Power System Technology，2009，33（2）：84-88，110.

［5］徐政.柔性直流输电系统［M］.北京：机械工业出版社，2012：2-9.

［6］胡永瑞.多端直流输电系统若干问题研究［D］.杭州：浙江大学，2013.HU Yongrui.Research on several issues in MTDC transmission system［D］.Hangzhou：Zhejiang University，2013.

［7］汤广福，罗湘，魏晓光，等.多端直流输电与直流电网技术［J］.中国电机工程学报，2013，33（10）：8-17.TANG Guangfu，LUO Xiang，WEI Xiaoguang，et al.Multi-terminal HVDC and DC-grid technology［J］.Proceedings of the CSEE，2013，33（10）：8-17.

［8］张文亮，汤涌，曾南超.多端高压直流输电技术及应用前景［J］.电网技术，2010，34（9）：1-6.ZHANG Wenliang，TANG Yong，ZENG Nanchao.Multi-terminal HVDC transmission technologies and its application prospects in China［J］.Power System Technology，2010，34（9）：1-6.

［9］范心明，管霖，夏成军，等.多电平柔性直流输电在风电接入中的应用［J］. 高电压技术，2013，39（2）：497-504.FAN Xinming，GUAN Lin，XIA Chengjun，et al.Multilevel VSCHVDC applied in wind power integration［J］.High Voltage Engineering，2013，39（2）：497-504.

［10］刘亚磊，李兴源，朱静，等.多端柔性直流输电系统在海上风电场并网中的应用［J］. 华东电力，2013，41（10）：2019-2022.LIU Yalei，LI Xingyuan，ZHU Jing，et al.Application of VSCMTDC in grid integration of offshore wind farms［J］.East China Electric Power，2013，41（10）：2019-2022.

［11］张静.VSC-HVDC控制策略研究［D］.杭州：浙江大学，2009.ZHANG Jing.Research on control strategies for VSC-HVDC［D］.Hangzhou：Zhejiang University，2009.

［12］张明兴.基于VSC的多端直流输电系统的运行控制研究［D］.成都：西南交通大学，2012.ZHANG Mingxing.Research ofVSC-MTDC operation and control［D］.Chengdu：Southwest Jiaotong University，2012.

［13］张桂斌，徐政，王广柱.基于VSC的直流输电系统的稳态建模及其非线性控制［J］. 中国电机工程学报，2002，22（1）：18-23.ZHANG Guibin，XU Zheng，WANG Guangzhu.Steady-state model and its nonlinear control of VSC-HVDC system［J］.Proceedings of the CSEE，2002，22（1）：18-23.

［14］付媛，王毅，张祥宇，等.多端电压源型直流系统的功率协调控制技术［J］. 电力自动化设备，2014，34（9）：130-136.FU Yuan，WANG Yi，ZHANG Xiangyu，et al.Coordinated power control of VSC-MTDC system［J］.Electric Power Automation Equipment，2014，34（9）：130-136.

［15］喻锋，王西田，解大，等.多端柔性直流下垂控制的功率参考值修正方法［J］. 电力自动化设备，2015，35（11）：117-122.YU Feng，WANG Xitian，XIE Da，et al.Power reference correction method for droop control of VSC-MTDC system［J］.Electric Power Automation Equipment，2015，35（11）：117-122.

［16］陈谦，唐国庆，王浔，等.多端VSC-HVDC系统交直流潮流计算［J］. 电力自动化设备，2005，25（6）：1-6.CHEN Qian，TANG Guoqing，WANG Xun，et al.AC-DC power flow algorithm for multi-terminal VSC-HVDC systems［J］.Electric Power Automation Equipment，2005，25（6）：1-6.

［17］郑超.实用柔性直流输电系统建模与仿真算法［J］.电网技术，2013，37（4）：1058-1063.ZHENG Chao.Studyonpracticalmodelingandsimulation algorithm for VSC-HVDC power transmission［J］.Power System Technology，2013，37（4）：1058-1063.

［18］季聪，卫志农，汤涌，等.基于自动微分技术的VSC-HVDC内点法最优潮流［J］. 电网技术，2012，36（10）：184-189.JI Cong，WEI Zhinong，TANG Yong，et al.A primal-dual interior point method-based algorithm adopting automatic differentiation for optimal power flow of AC/DC power grid containing VSC-HVDC system［J］.Power System Technology，2012，36（10）：184-189.

［19］卫志农，季聪，郑玉平，等.计及VSC-HVDC的交直流系统最优潮流统一混合算法［J］. 中国电机工程学报，2014，34（4）：635-643.WEI Zhinong，JI Cong，ZHENG Yuping，et al.Optimal power flow of AC-DC systems with VSC-HVDC based on a novel unified hybrid algorithm［J］.Proceedings of the CSEE，2014，34（4）：635-643.

［20］卫志农，季聪，孙国强，等.含VSC-HVDC的交直流系统内点法最优潮流计算［J］. 中国电机工程学报，2012，32（19）：89-95，190.WEI Zhinong，JI Cong，SUN Guoqiang，et al.Interior-point optimal power flow of AC-DC system with VSC-HVDC［J］.Proceedings of the CSEE，2012，32（19）：89-95，190.

［21］郑超，周孝信，李若梅，等.VSC-HVDC稳态特性与潮流算法的研究［J］. 中国电机工程学报，2005，25（6）：4-8.ZHENG Chao，ZHOU Xiaoxin，LI Ruomei，et al.Study on the steady characteristic and algorithm of power flow for VSC-HVDC［J］.Proceedings of the CSEE，2005，25（6）：4-8.

［22］郑超，盛灿辉.含VSC-HVDC的交直流混合系统潮流统一迭代求解算法［J］. 中国电力，2007，40（7）：65-69.ZHENG Chao，SHENG Canhui.Uniform iterative power flow algorithm for systems equipped with VSC-HVDCs［J］.Electric Power，2007，40（7）：65-69.?