CPS短路分断能力仿真及试验

黄世泽，郭其一 ，陈 杨，屠瑜权

（1.同济大学 道路与交通工程教育部重点实验室，上海 200331；2.同济大学 电子与信息工程学院，上海 200331；3.浙江中凯科技股份有限公司，浙江 杭州 325604）

0 引言

控制与保护开关电器（CPS）是一种同时具有控制与保护功能的集成式模块化多功能低压电器。KB0系列CPS作为填补国内空白的第一代CPS大类产品，采用模块化的单一产品结构型式，将主体三大组成部件即电磁传动机构、主电路接触组和操作机构有机地装配于一体，通过构件之间的关联动作以及部件之间的相互配合，解决了传统分立元件之间较难协调等被动问题，将分立元件的控制或保护功能完善可靠地集成统一于产品内部［1］。

短路分断过程在KB0系列CPS中对触头的分断能力、电寿命以及失效机理有很重要的作用。通常对短路分断过程的认识都是基于试验，对其中涉及到的电、磁、温度场及机械运动变化过程很难把握［2］。而通过对CPS短路分断过程的仿真研究，不仅能了解短路分断过程中导电回路的电动斥力、触头间的霍姆力、短路脱扣器的电磁吸力的大小和变化，通过理论分析得到短路分断过程中受力情况，形成完整的分断过程描述；还能分析电弧从触头到灭弧室的运动过程，从不同角度了解电弧的整体运动情况［3］。

目前，研究人员大多致力于通过微分方程建立电弧仿真模型的方式来加深对低压电器设备分断过程的认识［4］。而如何实现对CPS的动态分断过程进行较为完整的仿真研究是研究低压电器的一大难点［5］。

本文将虚拟样机仿真分析与数字化设计技术应用于KB0系列CPS的短路分断性能分析与优化设计中，采用有限元分析软件ANSYS计算短路分断过程中的作用力，结合触头系统机构运动数学模型与电弧模型，利用数值分析与计算软件MATLAB仿真执行短路分断时的构件关联及部件匹配动作过程，并通过仿真获取短路分断过程的动态特性，实现对整个CPS分断过程的研究，用于CPS短路保护装置的分析与优化设计［6-8］。

1 CPS接触组结构及分断原理

1.1 CPS接触组结构介绍

KB0系列CPS的主电路接触组主要由触头系统、容纳动/静触头的耐弧罩壳和设于其内的灭弧栅片组构成的灭弧室等构成［9］。触头系统既能接通、承载和分断正常条件下的电流，还能够接通、在规定时间内承载并分断规定的非正常条件下的电流，如短路电流。主电路接触组的构成示意图如图1所示。

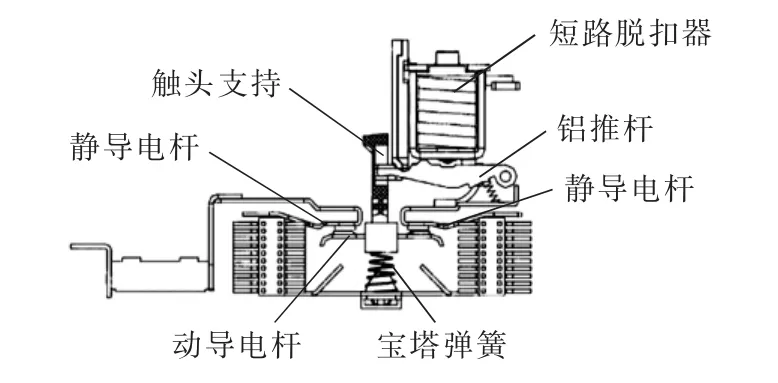
图1 主电路接触组构成示意图Fig．1 Schematic diagram of contact group for main circuit

短路脱扣装置主要由磁轭、设置于磁轭内部的动/静铁芯及弹簧等构成，用于检测短路电流，在过阈值时发出动作指令，并通过铝推杆将脱扣信号传递至触头系统。触头系统主要由动/静导电杆及其上的动/静触头、触头支持、宝塔弹簧等构成。当短路故障出现时，短路脱扣器内部动铁芯在短路电流产生的强大电磁场的作用下与静铁芯吸合，同时带动顶杆碰撞铝推杆，铝推杆联动触头支持向下移动加速分开触头，铝推杆下移一定距离时对锁扣的限位消失，锁扣在扭簧的作用下旋转至一定角度，旋转过程中带动操作机构内部的短路推杆滑移，从而引起操作机构的脱扣动作。在电弧熄灭后，短路脱扣器内磁场消失，动铁芯在压簧作用下回弹至磁轭板限位，铝推杆在压簧作用下返回旋转至锁扣限位，动导电杆携动触头在宝塔弹簧作用下往静触头方向回移直至触头支持被铝推杆限位，至此接触组内短路保护过程完成。操作机构脱扣致使电磁传动机构动铁芯释放，顶杆下移，使得触头保持在断开状态［10］。

1.2 CPS接触组的限流分断原理

接触组的分断能力是一个十分重要的性能指标，提高分断能力最重要的技术是限流技术。限流是指当短路电流通过该断路器时，其电流幅值和电流流过的时间应远小于预期短路电流，如图2所示。

本文利用断路器的等效电路图来分析它的限流分断原理，如图3所示。

图2 限流特性Fig．2 Characteristic of current limiting

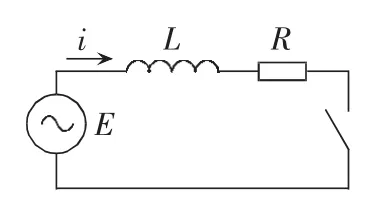
图3 断路器等效电路图Fig．3 Equivalent circuit of breaker

当电路发生短路时，有：

其中，L为线路电感；i为电弧电流；Uarc为电弧电压；E为电源电压；R为线路电阻。

为了简单说明问题，假定线路的电感值远大于线路电阻值，即 L≫R，则有 iR≈0，式（1）变为：

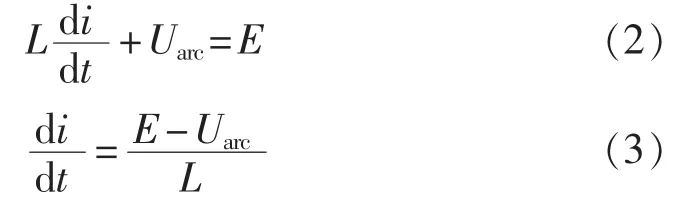
当 E-Uarc＞0 时，di/dt＞0，这表示电源电压大于电弧电压时，电弧电流处于上升阶段；当E-Uarc=0时，di/dt=0，这表示电源电压等于电弧电压时，电弧电流停止上升，达到最大值；当 E-Uarc＜0 时，di/dt＜0，这表示电源电压小于电弧电压时，电弧电流处于下降阶段。

所以，限制电流开始下降的条件是电弧电压大于电源电压。

2 CPS接触组短路分断过程及数学模型

本文研究对象为KB0系列CPS中的双断点限流触头系统。图4给出了系统的受力情况，整个触头系统包括3个反力弹簧，它们产生的反力分别是短路脱扣器内压力弹簧的反力、铝推杆的压力弹簧反力和动导电杆上的宝塔弹簧反力。系统的作用力为冲击电磁铁的吸力、触头间的电动斥力（只存在于触头闭合时）及导电回路的电动斥力。CPS短路分断可分为2个过程，第1个过程是机构动作过程，第2个过程是电弧运动过程和熄弧过程，前者主要由触头系统机构的机械动态方程来描述，后者主要决定于开断电弧的数学模型。

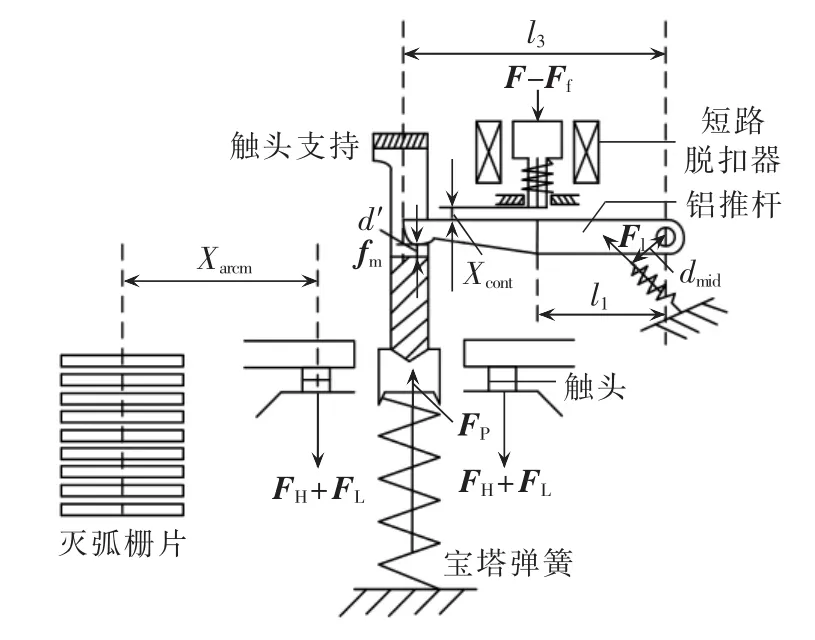
图4 双断点触头系统结构及受力图Fig．4 Structure and force diagram of double-break contact system

2.1 触头系统机构运动数学模型

a.短路脱扣器触动阶段：这一阶段从短路电流产生开始到短路脱扣器电磁吸力克服压缩弹簧的反力而使动铁芯开始动作瞬间结束。这一阶段电弧尚未出现，Uarc=0，但若短路电流通过触头回路产生的电动斥力足够大，就会使动、静触头斥开，产生电弧，这时电弧电压就不为零，而认为它约等于近极压降2U0=2×25=50（V）（U0是 1 对触头上的近极压降，由于是双断点所以乘2）。此时，机构尚未动作，只有电路瞬态方程：

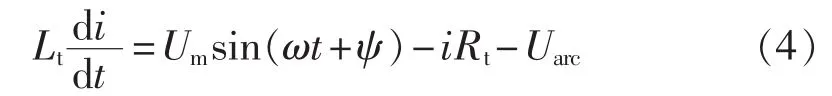
其中，Rt、Lt分别为短路回路的总电阻和总电感；ψ为电路合闸相角；Uarc为电弧电压；Um为电源电压的峰值。

b.动铁芯空载运动阶段：这一阶段从动铁芯开始运动开始到动铁芯顶杆碰到铝推杆瞬间结束。

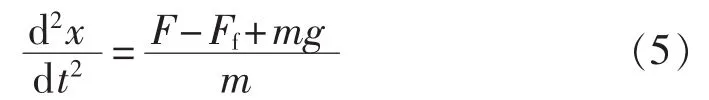
其中，F为冲击电磁铁的吸力；Ff为短路脱扣器内压缩弹簧的反力；x为铁芯行程；m为动铁芯质量；g为重力加速度。

c.动铁芯负载运动阶段：这一阶段从铝推杆开始转动开始到其顶端碰到触头支持瞬间结束。这一阶段的铁芯运动方程应计及铝推杆所受反力Fl，它的顶端所受摩擦力fm和转动惯量J作用，见式（6）。

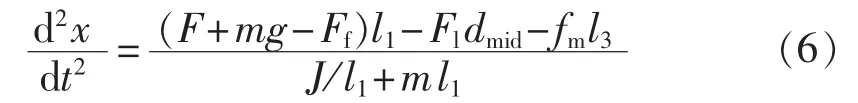
其中，l1为F-Ff的力臂；l3为宝塔弹簧力fm的力臂；dmid为铝推杆所受反力Fl的力臂。

d.电弧停滞阶段：这一阶段从动静触头分开开始到电弧达到某一长度结束。虽然此时电弧随着触头打开而产生，但其基本保持不变，所以这一阶段也称为电弧停滞阶段。这一阶段铁芯运动方程还应计及宝塔弹簧的反力作用：

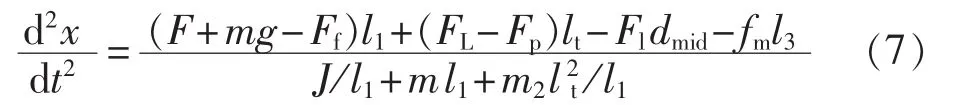
其中，FL为导电回路的电动斥力；Fp为作用于动触头杆的宝塔弹簧反力；m2为动触头杆质量；lt=l3cosθ，θ为转动杆的转角。

这一阶段的电弧电压为：

其中，garc为电弧电压梯度；d为触头的开距；xcont为短路脱扣器的顶杆与铝推杆之间的距离；d′为铝推杆与触头支持之间的距离。因为是双断点结构，所以电弧电压需要乘2。

2.2 电弧运动与熄灭过程的数学模型

a.电弧的运动阶段。

若忽略电弧的质量，认为电弧在运动过程中受电磁力和空气阻力的作用，在二力平衡条件下，应用经典的激波理论，电弧运动速度可用下式计算［11］：

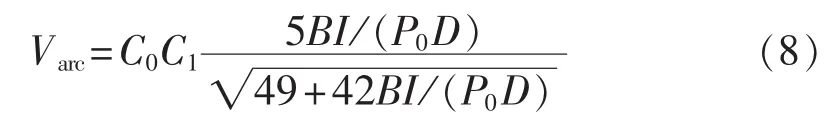
其中，C0=331.2 m/s，为空气中的声速；D为电弧直径；C1为考虑电弧反向转移现象后等效的电弧速度降低率，按实验数据C1取值为0.33；B为触头区自励磁场的磁场强度，本文通过ANSYS有限元仿真计算；I为电弧电流有效值；P0=0.101 3 MPa，为大气压力。

式（8）中电弧直径D是一个未知量，根据柯西电弧模型，从能量平衡出发，有：

其中，dQ/dt为单位长度电弧弧柱储能的变化；P为单位弧长的输入功率；Ps为单位弧长的功率损失。

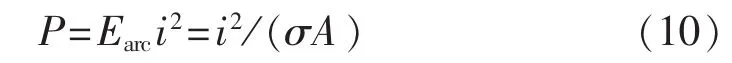
其中，Earc为电弧柱电场强度；i为电弧电流；σ为弧柱的导电率（（Ω·m）-1）；A=πD2/4，为弧柱的横截面积。

采用柯西电弧数学模型，认为单位体积弧柱中存储的能量为一常数，则单位长度电弧弧柱储能为：

能量的散出是由对流造成，Ps可由式（12）计算：

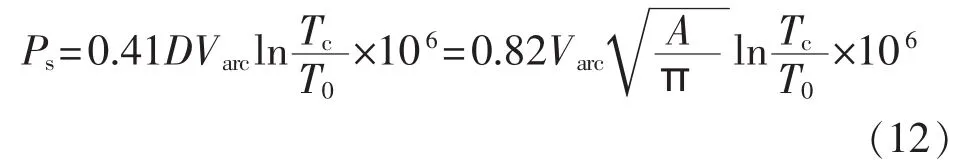
其中，Varc为电弧的运动速度（m /s）；Tc、T0分别为周围环境温度和电弧平均温度，计算中分别取237 K和15000 K。

将式（10）—（12）代入式（9），得到：

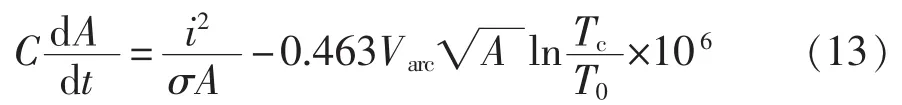
在电弧停滞阶段弧柱是很短的，可认为该阶段内无能量损失，输入的能量即为电弧储能量Q，因而Q可用数值积分求出：

认为t=ts时，电弧电流is与D的平方根成正比，即，考虑该瞬间弧柱长2mm，则有：

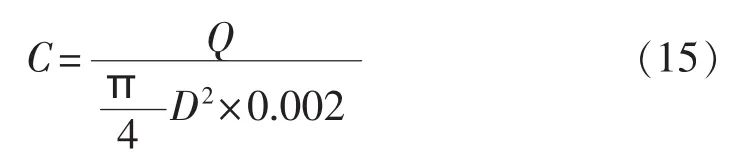
根据文献［12］，在 T0=15000 K 时，式（13）中的σ=10000（Ω·m）-1。

在电弧运动阶段，电弧电压Uarc为：

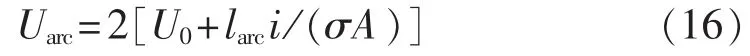
其中，larc为电弧长度，取为椭圆上弧线的1/4，椭圆的长短轴分别为触头开距和电弧弧根在与静触头相连的导弧板上的位移。

联立方程（4）、（8）、（13）、（16），即为电弧运动阶段的数学模型。求解联立方程组，就可获得电弧运动阶段的电弧电压Uarc、电流i、电弧运动速度Varc和电弧直径D。通过以上推导，得到了用微分方程描述的体现非线性的确定性电弧模型，它以能量守恒理论为基础，体现了电弧的主要物理特征。

b.电弧熄灭阶段。

电弧进入灭弧栅片后，即被分割成许多串联的短弧，若每一断口上有n片栅片（样机为10片），则电弧电压峰值为：

求解方程（4）、（17），直至 i=0，此时电弧熄灭，整个开断过程结束。

3 短路分断仿真分析

3.1 模型参数及主程序流程

由产品手册可知，C框架KB0产品短路脱扣器动铁芯的质量m=0.003 2 kg，动触头杆的质量m2=0.039 kg，其工作的额定电压为交流380 V或690 V，额定电流为45 A。仿真参数中，分断电压为380 V，预期分断电流为80 kA，功率因数为0.2，短路电流产生瞬间的电压导通角即电路合闸相角为105°［12］。

进行短路分断过程仿真时，需要确定触头系统的反力特性及一定气隙电流条件下系统作用力的二维表格，作用力由ANSYS软件获得。利用四阶龙格-库塔法求解上述数学模型中的微分方程组，可得到短路分断过程的动态特性。主程序流程如图5所示。

3.2 短路分断仿真结果

由ANSYS仿真可得分断电流的变化曲线如图6所示。动触头位移与速度变化曲线如图7所示。

从图6短路分断电流变化曲线中可以看出短路分断时间为2.335 ms，其中燃弧时间为1.515 ms，从短路电流产生到触头分开产生电弧的触动时间为0.82 ms，电弧停滞时间为0.404 ms。在电弧向灭弧栅片运动的过程中，短路电流达到峰值14.23 kA。从图7动触头位移与速度变化曲线中可以看出由于触头支撑杆的作用，动触头的最大位移为6 mm，而触头开距为3.5mm，动触头的最大速度可达到37.663m/s。

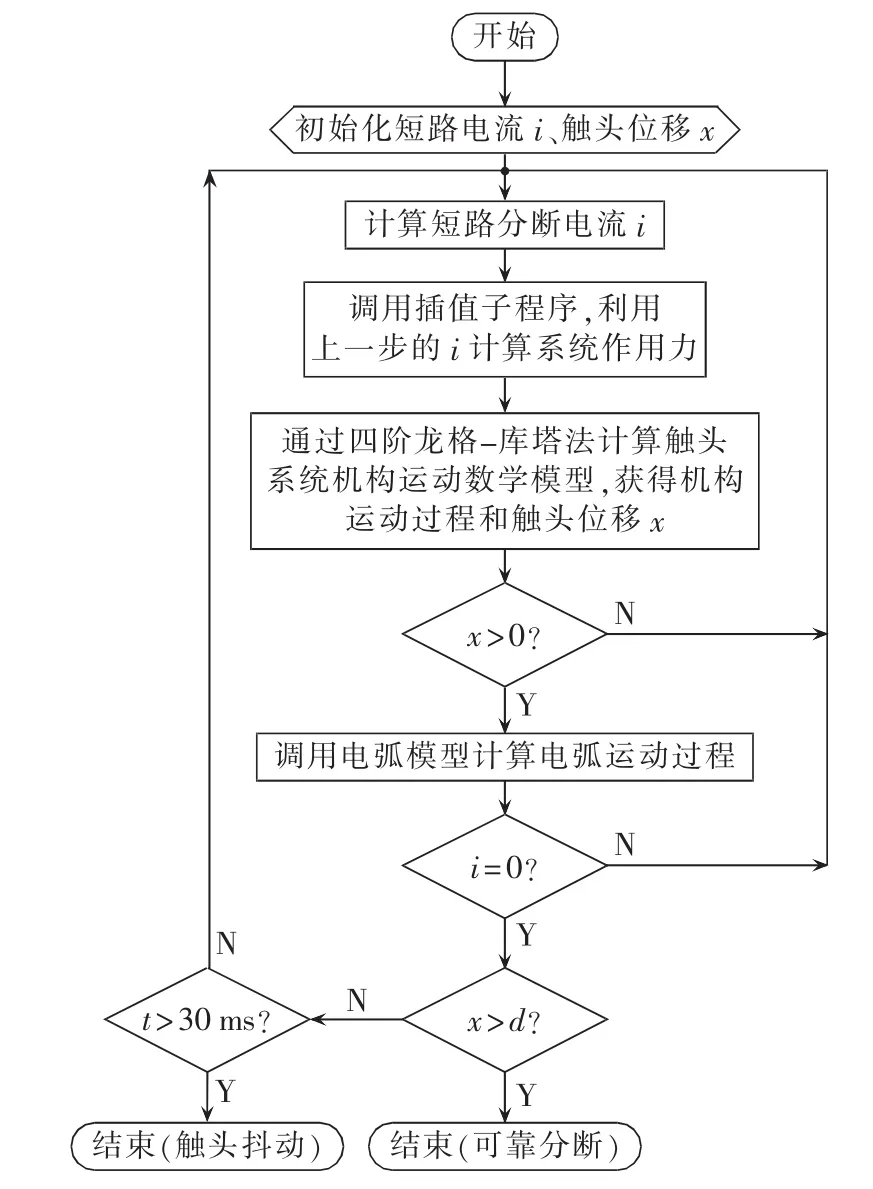
图5 短路分断仿真主程序流程图Fig．5 Flowchart of main program of short circuit breaking simulation

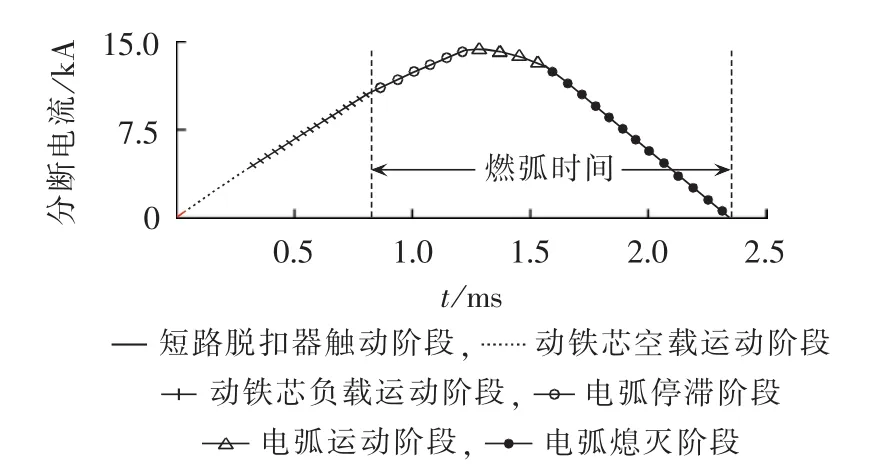
图6 短路电流仿真结果Fig．6 Simulative short circuit current

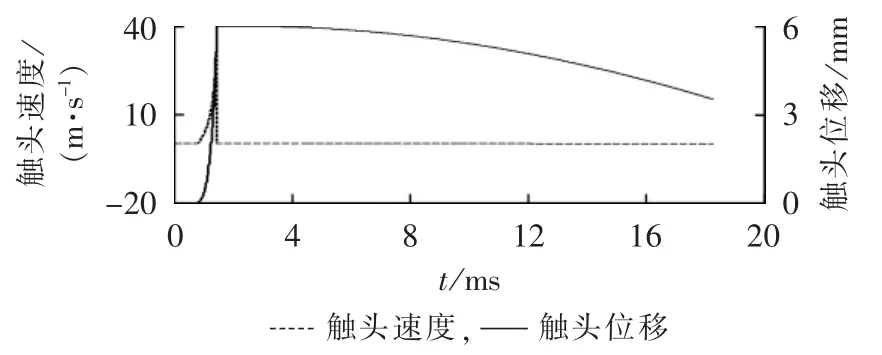
图7 动触头位移与速度的仿真结果Fig．7 Simulative displacement and velocity of movable contact

4 试验验证

4.1 额定运行短路分断能力（ICS）试验

对于CPS在自由空气中进行额定运行短路分断能力试验。对于额定运行短路分断能力试验，应在CPS可能会发生击穿现象的各个位置上按制造厂规定的距离及位置布置金属箔。试验电路如图8所示。图中，S1—S6表示电压传感器；D表示被试电器（包括连接电缆）；B表示整定用临时连接线。

图8 短路分断试验电路Fig．8 Circuit of short circuit breaking test

4.2 试验结果分析与验证

额定运行短路分断能力（ICS）试验电流波形如图9所示。

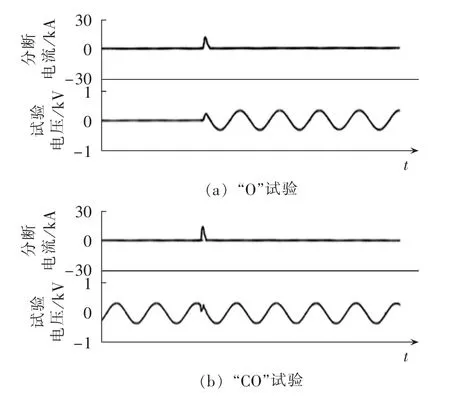
图9 试验电流波形Fig．9 Experimental current waveforms

在本次试验中，当试验电压为420 V、预期分断电流为81.4 kA时，“O”试验的A相分断电流峰值为9.86 kA，分断时间为 3.52 ms，燃弧时间为 3.69 ms；“CO”试验的A相分断电流峰值为13.7 kA，分断时间为2.64 ms，燃弧时间为1.73 ms，与仿真结果相似。

为了进一步验证仿真结果的正确性，表1详细列出了不同参数下的仿真结果与试验结果。

从表1中可以看出，仿真结果与试验结果存在一定的误差，但是整体上无论分断电流波形还是分断时间等都与仿真结果相似，其误差可能是由以下几个因素造成的：

a.仿真计算时，忽略了机构与机构之间摩擦力的影响；

b.在进行额定运行短路分断能力试验时，由于样机零件的分散性，实际接通电压、实际分断电流等与理论参数不一致。

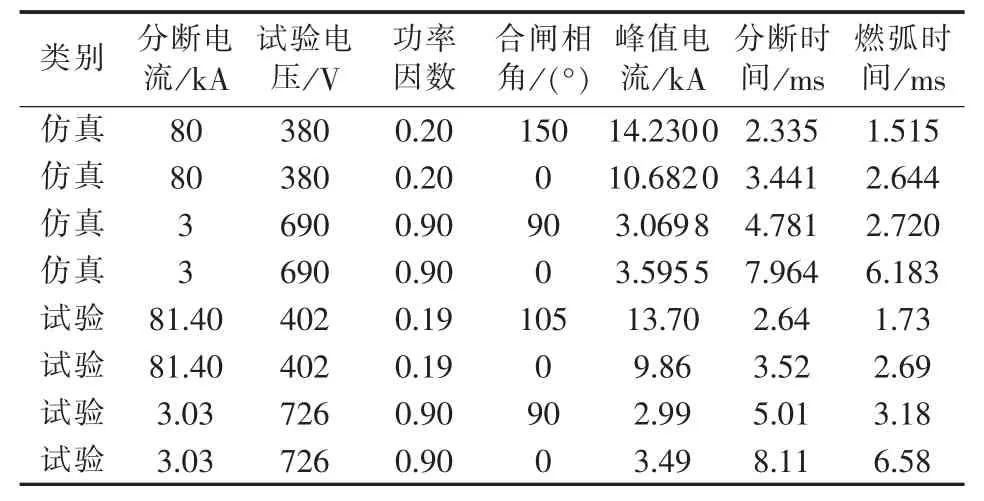
表1 不同参数下的仿真结果与试验结果比较Table1 Comparison of simulative and experimental results among different parameters

5 结论

控制与保护集成化是低压电器发展方向之一，短路分断是CPS的难点。本文针对KB0系列CPS的双断点限流触头系统的分断机理，将短路分断过程分为短路脱扣器触动阶段、铁芯空载运动阶段、铁芯负载运动阶段、电弧停滞阶段、电弧运动阶段及电弧熄灭阶段，并对各个阶段分别建立不同的数学模型。对380 V电压、80 kA电流情况下的电弧电流、触头速度、触头位移等进行仿真，同时也进行了额定运行短路分断试验，并对试验结果与仿真结果进行比较，验证仿真结果的正确性，为产品的设计提供科学依据。

［1］曾萍，胡景泰.新型电器——多功能集成化的“KB0系列控制保护开关”［J］. 电气传动，2001，31（6）：49-52.ZENG Ping，HU Jingtai.New type electrical apparatus-multifunctional and integrative“KB0 series control and protective switching devices”［J］.Electric Drive，2001，31（6）：49-52.

［2］GREGORY G D，HALL W M.Predicting molded-case circuit breaker let-through characteristics in an electrical system under short-circuit conditions［J］.IEEE Transactions on Industry Applications，1993，29（3）：548-556.

［3］WU Y，WU Y，RONG M，et al.Research on a novel two-stage direct current hybrid circuit breaker［J］.Review of Scientific Instruments，2014，85（8）：084707.

［4］XIANG B，LIU Z，GENG Y，etal.DC circuitbreakerusing superconductor for current limiting［J］.IEEE Transactions on Applied Superconductivity，2015，25（2）：1-7.

［5］HASSANPOOR A，HAFNER J，JACOBSON B.Technical assessment of load commutation switch in hybrid HVDC breaker［C］∥2014 International Power Electronics Conference（IPEC-Hiroshima 2014-ECCE-ASIA）.Hiroshima，Japan：IEEE，2014：3667-3673.

［6］SADI M A H，ALI M H.Transient stability enhancement by bridge type fault current limiter considering coordination with optimal reclosing of circuit breakers［J］.Electric Power Systems Research，2015（124）：160-172.

［7］MESSAL O，SIXDENIER F，MOREL L，et al.Simulation of low nickel content alloys for industrial ground fault circuit-breaker relays［J］.IEEE Transactions on Magnetics，2014，51（6）：1-9.

［8］NIAYESH K.Failure modes of synthetic test circuits used to evaluate the current interruption capability of high-voltage circuit breakers［J］.International Transactions on Electrical Energy Systems，2014（51）：4973-4984.

［9］LIU Y，YUAN H，CHEN D，et al.Experiment and simulation research on the influence of different main contact system on the interruption performance of control and protective switch［J］.IEEE Transactions on Power Delivery，2010，25（3）：1556-1563.

［10］邱建洪，潘礼纲，李华民，等.一种带短路保护功能的触头系统：CN101656178［P］.2010-02-24.

［11］BIZJAK G，POVH D.Circuit breaker model for digital simulation based on Mayr’s and Cassie’s differential arc equations［J］.IEEE Transactions on Power Delivery，1995，10（3）：1310-1315.

［12］BELBEL E M，LAURAIRE M.Behavior of switching arc in low-voltage limiter circuit breakers［J］.IEEE Transactions on Components，Hybrids，and Manufacturing Technology，1985，8（1）：3-12.