基于协同效应分析的输电线路脆弱评估方法

刘利民 ，刘俊勇 ，魏震波 ，龚 辉

（1．四川大学 电气信息学院，四川 成都 610065；2．国网长沙供电公司，湖南 长沙 410015）

0 引言

现代电力系统日益复杂化、扩大化和互联化，各区域装机容量快速增长，以满足高速发展的经济负荷需求。庞大电力网络能一定程度上提高系统运行效率，但自身的安全问题却日渐暴露。连锁故障大停电问题已成为现代电力系统安全稳定问题的主要威胁［1-3］。电网脆弱性对于研究连锁故障的引发和演变过程有着举足轻重的作用［4］。目前，脆弱性研究主要从结构脆弱性［5-11］与状态脆弱性［12-17］两方面展开。

电力系统结构脆弱性是指电网中某一元件或某一些元件退出或者相继退出后，系统保持其网络拓扑结构稳定的能力［5］。文献［6］将复杂网络理论应用到电网结构脆弱性分析上，并定义了带权重的介数用以评估结构脆弱性。文献［7］考虑了电力系统实际物理特性，定义了以电抗为权重的最短路径和失负荷百分比及输电效率，研究了小世界电网连锁故障发展的广度和深度。文献［8］对介数指标作出改进，提出了适合电力系统的输电介数评估指标，结合网络能力评估了母线重要性。更进一步，文献［9］以网络最大流为基础，结合功率传输分布因子（PTDF），分别构建了线路和节点的传输贡献度指标以衡量线路的节点的关键性。

电力系统状态脆弱性是指系统在遭受扰动或故障后，元件状态变量发生变化，并可能向临界值逼近的特性［10］。文献［11］基于事故链模型推导了事故发生的概率，结合事故发生引起的电压、频率和功率等变化的后果严重度，构建了系统的输电脆弱度风险评估模型。文献［12］将熵引入电力系统，利用熵将故障扰动给系统元件带来的功率冲击结合到一起，量化了扰动给不同元件带来的冲击不均衡性，并建立了潮流熵的脆弱元件辨识模型。文献［13］深度挖掘电力系统本身特性，定义了节点的电气耦合连接度以评价电网节点的关键性。文献［14］基于潮流追踪，集合功率输送、网络结构和运行状态等，分别提出了线路功率介数和节点功率介数等元件关键性辨识指标。文献［15］为弥补潮流熵、节点电压偏移和节点重要度3种评价指标的不足，提出一种综合脆弱性指标，并以长沙电网和IEEE39节点系统仿真验证了指标的合理性。

然而在实际情况中，电网网络结构和运行状态两者是相互关联的，共同决定系统安全［8］。单一从其中一个角度评价电力系统的脆弱性存在不足［12］。而上述关于结构脆弱性的研究并没有充分兼顾考虑运行状态带来的影响；关于状态脆弱性的研究多数也仅从电网运行状态视角评估系统的脆弱性。仅有少数文献能够同时考虑两者，如文献［10，14-17］等。其中，文献［16］提出了从全局和局部、有功和无功两方面综合衡量输电线路脆弱度的方法；文献［17］中则提出了网络元件受扰动后所表现出的脆弱程度是自身抗干扰能力与网络传导能力的综合表现的观点，分别采用负荷水平与线路潮流分布给予量化，并以两者乘积作为评估结果。这些文献在一定程度上兼顾了电网结构与运行状态，但并未对结构脆弱性和状态脆弱性之间的关联关系进行充分的研究和阐述。

为解决上述问题，本文首先在结构性视角下，基于复杂网络理论，挖掘电力系统实际特性，提出电网的结构脆弱性评估指标；然后，利用功率传输裕度和过载，结合线路开断功率分布因子，构建电网的状态脆弱性评估指标；再次，研究结构脆弱性与状态脆弱性之间的关联关系，指出两者之间存在的协同效应，并建立线路的综合脆弱性评估模型；最后，通过对新英格兰39节点系统仿真计算，验证本文所提改进模型的正确性和合理性。

1 电网结构脆弱性指标

电网结构脆弱性的研究主要采用复杂网络理论工具［5-9］。而由于电力系统的实际特性所在，复杂网络中的度数、介数等概念并不完全适用于电力系统。比如，度数反映的是网络局部结构特征，与实际电网的全局联系不大；介数假定潮流在任意2个节点间沿最短路径传输，与电力系统实际特性相违背。

电网的网架结构决定了系统的传输能力，系统的传输能力与实时运行状态无关。本文从输电线路的输电容量出发，结合PTDF，基于介数概念，以建立电网结构脆弱性指标。

设输电通道gd由发电机g、负荷d和若干线路li（i=1，2，…，n，其中 n 为发电机 g 到负荷 d 的输电通道的线路总数）组成。线路集｛li｝的最大传输功率为 Plimax，其相对于发电机g和负荷d的 PTDF［9］为Fli，gd，那么输电通道gd的传输容量为：

由于PTDF量化的是节点对（g，d）间的功率传输对各支路的利用情况，即各支路对潮流传输贡献的灵敏度，因此，上式物理意义在于：输电通道gd间的实际传输容量应为线路集｛li｝中有线路达到传输容量上限时所对应的潮流分布。显然，当系统网架结构一定时，系统的输电能力亦确定，它不会随系统运行状态变化而变化。

值得注意的是，电力系统是一个具有高度非线性特征的有权网络；潮流并不沿着最短路径流动，而是所有线路都可能有流动；潮流不是在网络中任意2个节点间随意流动，而是从发电机节点流向负荷节点。故复杂网络中的介数定义，包括文献［8］中所定义的介数并不完全适用于电力系统。因此，本文提出由式（1）中的输电容量来重新定义线路介数。

定义线路li在输电通道gd之间的源荷介数为：

上式物理含义在于：对于源荷节点对gd，当源点g与负荷点d之间传输的功率达到网络容许的最大值时线路li所承载的潮流。那么，在整个系统Ω中，线路li的源荷介数应是所有输电通道在线路li上的叠加，即有：

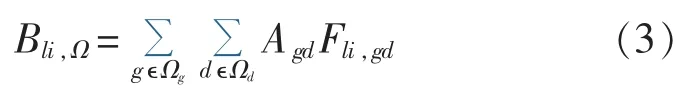
其中，Ωg为网络Ω中的发电机节点集；Ωd为网络Ω中的负荷节点集。

显然，上式中线路li源荷介数的实质是支撑多个源荷通道传输功率的线路li的传输容量。进一步考虑情况如图1所示。

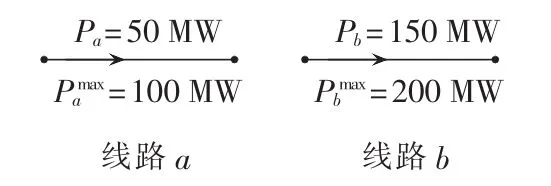
图1 线路传输功率示意图Fig.1 Schematic diagram of power transmission lines

图中，线路a和线路b的传输绝对裕度均为50 MW，但线路a负载率0.5低于线路b的0.75，从安全性角度而言，a较b好。因此，为修正绝对传输容量表征上的缺陷，将式（3）作如下处理：

其中，αstructure（li）为线路 li的结构脆弱性指标。

该定义不仅刻画了潮流分布情况（Fli，gd因子作用），且弥补了以往介数潮流只沿最短路径流动和潮流在任意两节点间流动的不足，同时消除了因线路传输容量不同带来的影响。其中需要指出的是，该指标中，源荷点对是平权的。但在实际电网中，并不是所有源荷点对的传输需求都一样，而是视运行方式而有所侧重。但为了该指标只与系统的网架结构发生关系，故未加入运行方式的影响，即与系统运行状态无关，因此，该指标属于一个典型的结构性脆弱指标，符合结构脆弱性评估要求。

2 电网状态脆弱性指标

状态脆弱性通常采用功率、电压、相角等物理电气量的变化进行刻画。为了与前文中结构指标考虑角度一致，本文选择功率状态变量。

根据状态脆弱性与功率分布因子定义，线路y相对于线路x的线路停运功率分布因子为Fy-x。在t时刻，若线路y停运后造成系统功率损失Py，则其中线路y停运对线路x造成的功率冲击为：

那么t+1时刻，线路x的传输功率为：

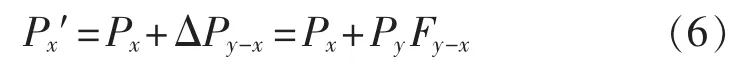
显然，当t+1时刻支路x的传输功率Px′小于最大传输功率Pxmax时，不会对系统造成影响；但是，当传输功率Px′大于等于Pxmax时，其停运概率随功率增加而增加，且有近似线性关系［18］，如图2所示。图中，px为支路x的停运概率；为支路x处于正常潮流水平运行时的停运概率，可由历史数据统计得到。线路y故障给支路x造成的功率过载量为：

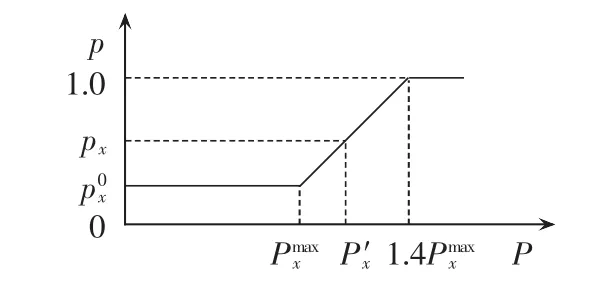
图2 线路停运概率模型Fig.2 Probability model of line failure

进一步，将上式进行归一化：

其中，SB为基准功率。

那么，线路y停运给其他线路造成的功率过载量为：

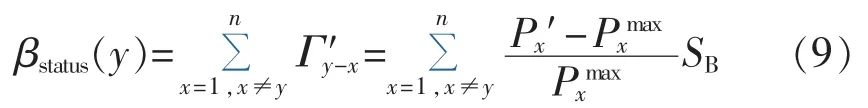
其中，n为系统线路总数。

选取上式功率过载量βstatus（y）作为电网状态脆弱性评价指标。不难发现：该值越大，说明线路停运后给系统其他线路的造成传输功率转移影响相对较大，即越逼近线路或系统极限传输功率，发生过载或相继过载停运概率就越高，因此系统越脆弱。

3 协同效应及综合脆弱模型

前文研究表明：结构和状态是评估系统脆弱性的2个不同角度，但单一从其中一个角度评价系统脆弱性势必存在不足［10］。如何兼顾两者是关键。

首先，利用“木桶原理”来阐释结构与状态间的关联关系。一个木桶盛水的最大容量取决于木桶的结构，木桶容积可以类比为电网的传输容量。木桶上最短的那块木板实际是盛水多少的决定性因素，可称之为结构性缺陷。木桶里面盛水的多少可类比为电网线路上的潮流水平。装水量太多，超过了木桶的承受能力会溢出，类比为系统的潮流水平过高，会使得输电线路过载停运。显然，木桶是否漏水是由木桶结构和状态同时决定的。结构性缺陷固然会制约电网的实际输电能力，但实际运行状态也对电网的传输功率能力有着重要影响。外界影响因素不能从根本上改变本身固有的结构脆弱性，但合理安排电网的结构将更有助于提高电网的可靠性和稳定性水平［7］。

一般地，合理地倾斜木桶，避开最短木板，就能够装更多的水。即有效降低短板处实际水平面高度，类比为降低传输容量裕度最小线路的负载水平，则可传输更多功率。但值得注意的是，“倾斜”（即改变运行方式）的前提是功率转移不会造成其他线路越限，即系统其他线路需有一定裕量承担“倾斜”带来的功率转移。因此，这就要求原系统负载水平不能太高。显然，当系统负载水平越低时，“倾斜”影响就越小，反之越大。这表明：结构（系统传输极限）与状态（实际传输容量）之间是相互关联的，存在协同效应［19］。特别是在系统满载时，两者的协同效应最强，表现出的共同作用最强，微小的干扰会被放大很多倍（级联效应），且可能导致系统整体的崩溃。

因此，考虑到系统结构和状态之间的这种协同效应，提出基于协同效应的电网线路脆弱性的综合评估模型如下：

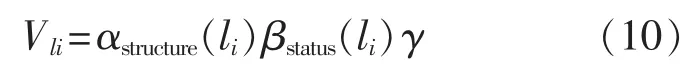
其中，γ为结构与状态关联因子，取为γ=P/Pmax，P为实时功率，γ的物理意义为线路负载率。

4 算例分析

4.1 标准节点系统仿真分析

选取新英格兰10机39节点系统为例（如图3所示）。系统参数见文献［20］。

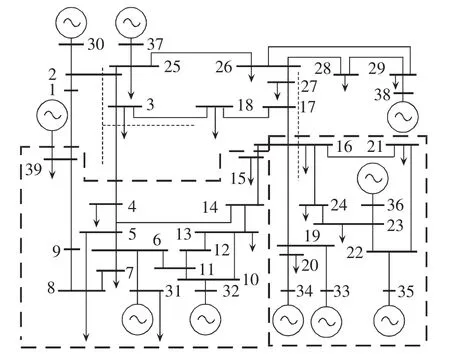
图3 新英格兰39节点系统Fig.3 New England 39-bus system

4.1.1 结构脆弱度

利用式（1）—（4）计算系统46条线路的源荷介数，结果展示于图4，线路编号见表1。

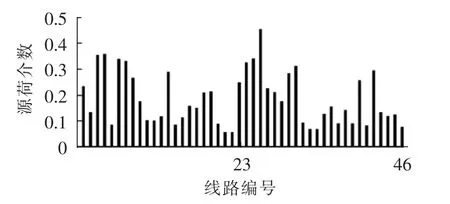
图4 线路结构脆弱强度值Fig.4 Structural vulnerability for lines

不难发现，源荷介数较高的前9条线路线路全部集中在图3中的细虚线区域。该虚线区域为整个网络的核心汇集区域，是发电机外送功率的重要通道，起着中枢连接作用，结构重要性不言而喻。这些线路的故障将直接造成发电机与负荷间脱节，发电机无法输送功率，负荷无法获得足够的功率支撑。线路16-17、15-16和14-15等是图3中右下方粗虚线框的发电机密集区域与中部3号和18号负荷节点及左下方粗虚线框重负荷区域之间的重要联络线。这些线路的断开将直接导致33号、34号、35号和36号发电机的功率无法外送，甚至导致图3中右下方粗虚线框与系统脱离，形成孤岛。而线路2-25、2-3、3-4、3-18 和 26-27 则是 30 号、37 号和38号发电机向负荷区域外送功率的重要通道，一旦故障，将导致3和18号负荷节点以及左下方的粗虚线框负荷区域无法获得足够的功率支撑。

进一步，将结构脆弱值排序前10位的线路与文献［9］结果对比，如表2所示。

表1 IEEE 39节点系统线路编号Table 1 Number for lines of IEEE 39-bus system

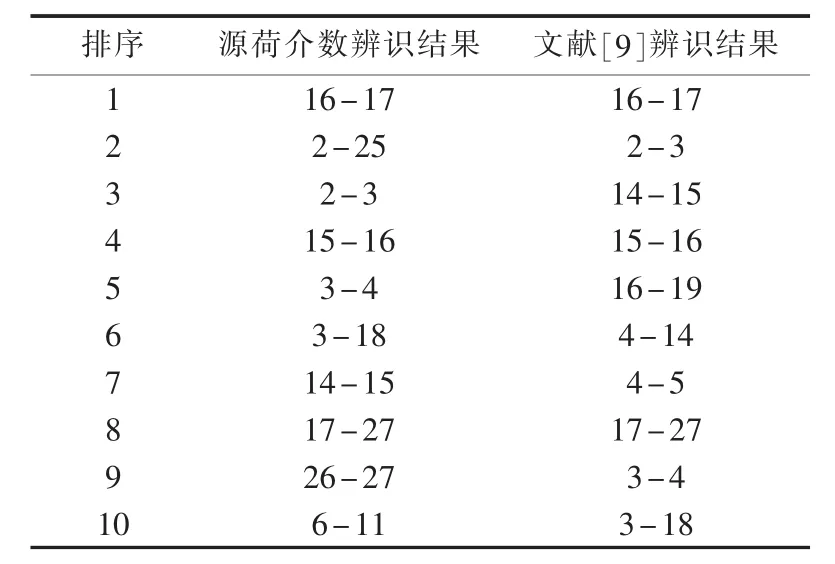
表2 结果对比（I）Table 2 Top 10 of structurally vulnerable line（I）

可看出，源荷介数和最大流传输贡献度的辨识结果大同小异，前10条线路中有7条相同，这说明了源荷介数作为电网结构脆弱线路彼辨识的有效性。 在源荷介数辨识结果中，有线路2-25、26-27、6-11未出现在最大流传输贡献度的辨识结果中，这主要是由源荷介数与最大流传输贡献度的指标构建的不同造成的。最大流为所有输电通道中最小线路容量的累加，而源荷介数是每条输电通道最大输送功率时各线路承担功率的叠加，并有效消除了不同线路传输容量带来的影响，更贴近电力系统实际，故认为源荷介数用于结构脆弱性更为合理。

4.1.2 状态脆弱度

据式（5）—（10）计算每条线路的状态脆弱性，取值排序前10位线路如表3所示。

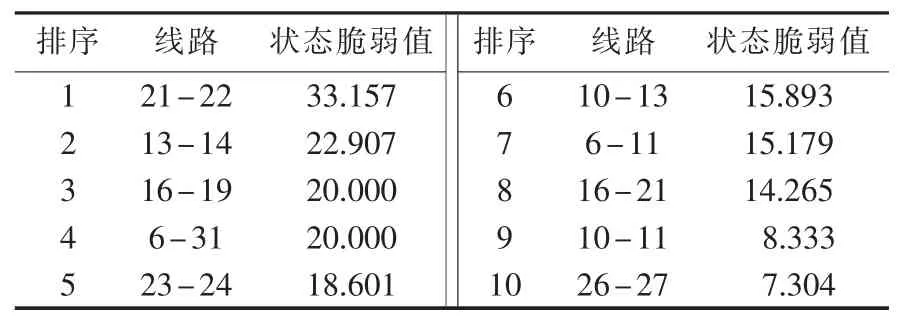
表3 线路状态脆弱强度值Table 3 Top 10 of conditionally vulnerable line

结合IEEE 39节点稳态数据分析发现，表3中的线路多数承担着较大的功率，其中以线路21-22和6-31承担功率最大，分别承担着604MW和668 MW的功率。如此大的功率承载，在线路故障后，将导致系统其他线路功率过载。如线路21-22故障导致线路16-24过载28.9 MW，线路22-23过载50 MW，线路23-24过载358.5 MW，根据各线路的传输容量限制与图2的线路停运概率模型，线路23-24将直接因过载过多而断开，进一步演变将是线路22-23和23-36过载断开，系统失去35号和36号发电机；同时，线路23-24故障后会引起线路4-5、10-13和13-14的故障概率剧增，若线路4-5、10-13和13-14中有一条线路故障将会导致发电机跑飞、潮流畸变，引起大停电。若线路6-31故障，将导致系统直接失去31号发电机，同时为满足系统负荷需求，其他发电机（如30号）不得不增加出力，从而导致潮流变化，线路6-11过载104 MW，据图2的线路停运概率模型，线路6-11将直接过载断开，从而引起包括线路16-17（结构脆弱值最高）和21-22（状态脆弱值最高）等在内的多条线路停运，导致系统解列。稳态时，线路13-14承担功率为317 MW，虽然不如线路21-22和6-31多，但由于支路开断功率分布因子的缘故，使得线路13-14故障将导致线路6-11过载137 MW和线路10-11过载17 MW。据图2的线路停运概率模型，线路6-11亦直接过载断开，系统失去32号发电机和12、13号节点负荷，其他发电机不得不弥补32号发电机的650 MW功率缺额，造成线路10-11与10-13严重过载，发电机出力透支而停运，进而导致更多线路停运（如线路2-3和3-4等）和发电机停运（如30号等），引起大停电。同排在表3中第3的线路16-19承担着451MW的功率，是33号和34号发电机与系统其他元件相连的唯一通道，其重要程度不言而喻。表3中排名第10的线路26-27在稳态时承担功率257MW，为表3中所有线路中承担功率最低。其故障断开将引起线路2-3功率过载36.5 MW，加大了线路2-3的故障概率，给系统带来了更大的危险和隐患。上述分析说明，状态脆弱性指标是有效的。

4.1.3 基于协同效应的综合脆弱度

从4.1.1和4.1.2节的结果可以看出，结构脆弱性与状态脆弱性的辨识结果并不相同。这主要是因为两者评估角度不同，结构主要体现在系统保持网络拓扑稳定性的能力上，而状态主要为系统的状态量的变化，并向临界值逼近的特性。

据式（10）评估每条线路的综合脆弱强度，结果如图5所示。

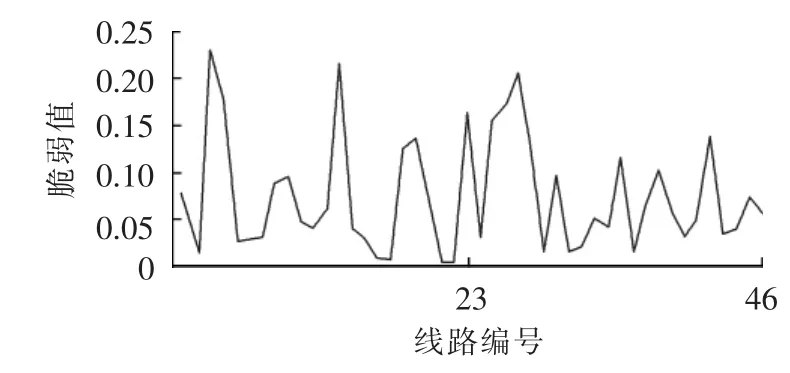
图5 IEEE 39节点系统线路脆弱强度值Fig.5 Line vulnerabilities of IEEE 39-bus system

以图5中3个尖峰3、13和27（分别代表线路2-3、6-11和16-19）为例分析说明。线路2-3为30号和37号发电机外送功率的通道，结构上很重要；其故障没有造成其他支路过载故障，但是其0.64的负载率，即结构与状态之间较高的协同效应使线路2-3为最为脆弱的线路；线路6-11在表2中排列第10，其故障会造成线路10-13、4-14和13-14等过载，且0.65的负载率使状态与结构之间的协同效应较强；线路16-19在结构脆弱性上排列不靠前，但其0.75的负载率承担着451 MW的功率，为33号和34号发电机与系统其他元件相连的唯一通道，模拟发现，断开线路16-19，将直接导致系统失去33号和34号发电机，为满足负荷需求，系统需加大其他发电机的出力，31号发电机需增加出力455 MW，这超过了31号发电机的额定功率（750 MW）382 MW，会造成31号发电机停运，进而引起系统更大的功率缺额，导致大停电。线路3-4和14-15分别是图3中上方区域和右下方粗线框区域向左下方粗线框区域输送电能的通道，在表2中分列第5和第7，但是两者断开都不会造成其他线路过载，分别只有0.075和0.084的负载率，结构与状态之间的协同效应弱，所以并未进入综合脆弱性前列。

选取脆弱值前10的线路列于表4中，并与文献［6］和［15］的结果进行对比，来验证本文所提方法的有效性和合理性。

从表4可看出，本文方法识别出的脆弱线路与文献［6］识别出的脆弱线路有6条相同（2-3、16-19、2-25、16-17、15-16 和 16-21），且 2-25、16-17 和15-16等脆弱线路在本文方法中排列4、5和7，说明了本文所提方法的有效性。本文所提方法与文献［6］结果不同的原因在于文献［6］是从结构性视角出发，定义了带权重的介数以评估结构脆弱性。而本文方法充分考虑了结构与状态之间的协同效应，兼顾两者而定义的综合脆弱指标较于文献［6］更合理有效。文献［15］综合了潮流熵、电压和节点重要度，从状态和结构方面评估了电网线路脆弱性，结果如表4所示。从结果可看出，本文方法与其有相同之处，如线路2-3、2-25、16-17和15-16这4条脆弱线路。两者的不同之处主要是指标的构建方式不同，文献［15］通过设置修正系数将状态与结构结合到一起，而本文方法深度挖掘了结构与状态之间的关系，指出两者之间的协同效应，根据协同效应构建的综合脆弱指标，结果更符合电力系统实际情况。

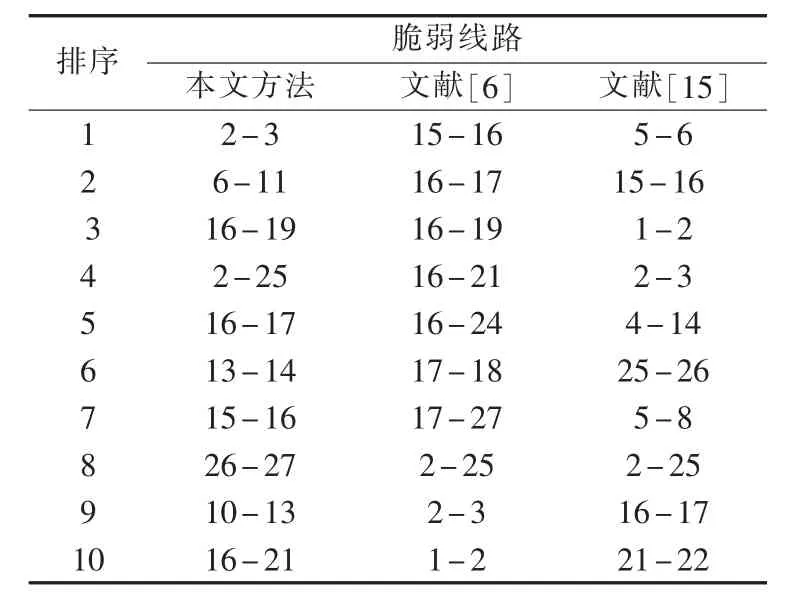
表4 结果对比（Ⅱ）Table 4 Top 10 of vulnerable line（Ⅱ）

4.2 某省网500 kV网架实例分析

图6为某省500 kV网架系统简化拓扑。该省水电资源丰富，水电装机容量占总装机容量70%，主要集中在西部高海拔地区，需经过长距离输送达到负荷中心。根据2013年丰水期系统数据，计算线路的结构、状态和综合脆弱度，且作归一化处理，分别取各排序前10位列于表5。

图6 某500 kV网架拓扑结构Fig.6 Topology of a 500 kV system

结合图6和表5可以看出，在结构上比较脆弱的线路主要为中枢连接通道，是连接发电机和负荷的重要通道，如线路23-29、12-14和38-43等。结果与新英格兰39节点系统仿真结果基本一致，说明了源荷介数用于评估线路结构脆弱性的有效性。这些线路一旦故障断开，将直接导致电源与负荷失联，功率无法外送，负荷无法得到足够功率支撑而被切除，使得系统失去更多的发电机和负荷。线路1-2为发电机输出线，其排序较高，结构上比较脆弱是因为在丰水期，1号水电厂满发，承担着580 MW的功率外送，一旦唯一的功率输送通道1-2故障断开，将导致2、3、4等负荷节点580 MW的功率缺额，为满足负荷需求，不得不加大6号、11号等其他电厂的出力，一旦这些电厂出力无法增加满足，系统将失去更多负荷。

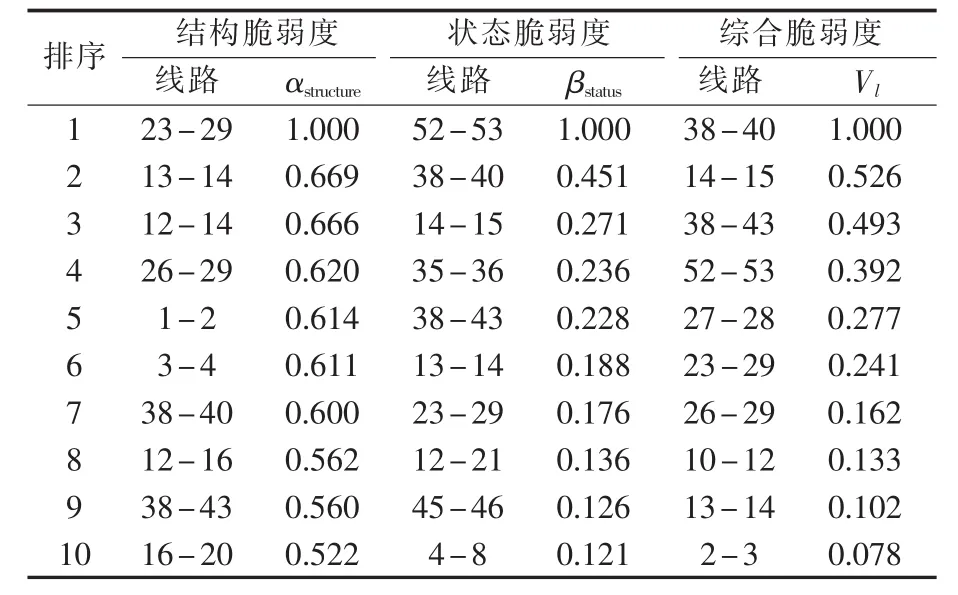
表5 某500 kV网架脆弱线路Table 5 Top 10 vulnerable lines of 500 kV system

结合系统稳态数据，从图6和表5知，状态脆弱值较高的线路都承载着较大的功率输送，多集中在大型发电厂功率输送通道，如线路52-53、38-40、14-15和35-36等。计算结果与新英格兰39节点系统结果大致相同，证明了本文状态脆弱性指标用于评估线路状态脆弱性的有效性。线路52-53为53号火电厂功率外送的唯一通道。计算结果表明，该线路断开，系统失去955MW的功率出力，引起1号、6号和11号发电厂增加出力，造成线路4-49过载发热故障，导致进一步的连锁反应。线路38-40是37号水电厂往系统输送功率的主要通道，承载着1973 MW的功率输送；线路38-43是35号和37号水电厂西电东送的必经通道，承载着2 465.6 MW的功率外送；线路14-15承担着15号发电厂981.6MW的功率外送。

表5脆弱排序显示，结构脆弱性、状态脆弱性和综合脆弱性排序前10的共同线路有4条，分别是线路23-29、线路13-14、线路38-40和线路38-43。上述分析中，线路38-40是31号大型水电厂供电的主要通道，结构上比较重要，承载着1973 MW的功率外送，加上其0.62的较高负载率，使得结构与状态之间的协同效应较强，成为最为脆弱的输电线路。线路38-43则是该省西电东送的重要通道，也有着较强的协同效应（负载率0.63），是比较脆弱的线路之一。线路23-29结构上最为脆弱，承载功率842.7 MW，但是其设计时，额定容量较大，在当前运行方式下负载率仅为0.26，结构脆弱性与状态脆弱性之间的协同效应较弱，导致综合脆弱排名不高。同样，因为额定容量较大，15号发电厂满发时线路 13-14的负载率亦只有0.14，此时结构状态之间的协同效应较弱，因此其综合脆弱度不高。

进一步，对综合脆弱排序前10的线路分别进行N-1系统稳定性分析。在线路设置三相接地短路故障，0.2 s解除，观察发电机功角和电压稳定。仿真实验结果如表6所示，可以发现，线路38-40、14-15、23-29、52-53和 27-28故障，电源功率无法外送，系统功率大量短缺，造成系统功角失稳；而线路38-40、38-43、23-29、26-29 和 13-14 故障使得区域功率支撑不足，造成系统电压失稳，其中线路38-40与38-43故障为双失稳；另外较为明显的是，随着线路综合脆弱度的降低，系统失稳现象显著改变，从双失稳到单失稳，从失稳到不失稳，趋势明显。如线路10-12与2-3故障已不会造成系统失稳。该结果表明综合脆弱度能较准确地刻画系统线路的实时运行状况，验证了本文方法的合理性与有效性。

表6 线路故障失稳类型Table 6 Instability types by line fault

5 结论

本文通过分析结构与状态及其关联关系对电网脆弱特性的影响，提出计及三方面因素的电网综合脆弱评估模型。研究结果表明，综合脆弱评估思想更符合现代电网属于复杂性系统的特征。为探索其脆弱本质和定位薄弱环节，需要有效量化个体与整体间的关联关系。其次，较现有方法，它克服了过去结构或状态脆弱评估考虑因子不全面的弊端，且通过协同效应因子量化了的两者关联关系，提升了综合脆弱辨识能力与精度。下一步，将系统动态过程考虑其中，实现电力系统薄弱环节全过程评估是研究重点。

［1］IAN D.Estimating the propagation and extent of cascading line outages from utility data with a branching process［J］.IEEE Transactions on Power Systems，2012，27（4）：2146-2155.

［2］PIERRE H，PIERRE-ETIENNE L，JEAN-CLAUDE M.Blackout probabilistic risk assessmentand thermaleffects：impacts of changes in generation［J］.IEEE Transactions on Power Systems，2013，28（4）：4722-4731.

［3］李扬，苏慧玲.N-k故障下影响电力系统脆弱性的关键线路研究［J］. 电力自动化设备，2015，35（3）：60-67 LI Yang，SU Huiling.Criticalline affecting power system vulnerability under N-k contingency condition［J］.Electric Power Automation Equipment，2015，35（3）：60-67.

［4］苏慧玲，李扬.基于电力系统复杂网络特征的电路脆弱性风险分析［J］. 电力自动化设备，2014，34（2）：101-107.SU Huiling，LI Yang.Line vulnerability risk analysis based on complex network characteristics of power system［J］.Electric Power Automation Equipment，2014，34（2）：101-107.

［5］魏震波，刘俊勇，朱国俊，等.基于可靠性加权拓扑模型下的电网脆弱性评估模型［J］. 电工技术学报，2010，25（8）：131-137.WEI Zhenbo，LIU Junyong，ZHU Guojun，et al.Vulnerability evaluation model to power grid based on reliability-parameter-weighted topological model［J］.Transactions of China Electrotechnical Society，2010，25（8）：131-137.

［6］曹一家，陈晓刚，孙可.基于复杂网络理论的大型电力系统脆弱线路辩识［J］. 电力自动化设备，2006，26（12）：1-5，31.CAO Yijia，CHEN Xiaogang，SUN Ke.Identification of vulnerable lines in power grid based on complex network theory［J］.Electric Power Automation Equipment，2006，26（12）：1-5，31.

［7］丁明，韩平平.加权拓扑模型下的小世界电网脆弱性评估［J］.中国电机工程学报，2008，28（10）：20-25.DING Ming，HAN Pingping.Vulnerability assessment to smallworld powergrid based on weighted topologicalmodel［J］.Proceedings of the CSEE，2008，28（10）：20-25.

［8］BOMPARD E，PONS E，WU Di.Extended topological metrics for the analysis of power grid vulnerability［J］.IEEE Systems Journal，2012，6（3）：481-487.

［9］鞠文云，李银红.基于最大流传输贡献度的电力网关键线路和节点辩识［J］. 电力系统自动化，2012，36（9）：6-12.JU Wenyun，LIYinhong.Identification ofcriticallinesand nodesin powergrid based on maximum flow transmission contribution degree［J］.Automation of Electric Power Systems，2012，36（9）：6-12.

［10］魏震波，刘俊勇，朱国俊，等.基于电网状态与结构的综合脆弱评估模型［J］. 电力系统自动化，2009，33（8）：11-14，55.WEI Zhenbo，LIU Junyong，ZHU Guojun，et al. A new integrative vulnerability evaluation model to power grid based on running state and structure ［J］.Automation of Electric Power Systems，2009，33（8）：11-14，55.

［11］WANG Ansi，LUO Yi，TU Guangyu，et al.Vulnerability assessment scheme for power system transmission networks based on the fault chain theory［J］.IEEE Transactions on Power Systems，2011，26（1）：442-450.

［12］李勇，刘俊勇，刘晓宇，等.基于潮流熵的电网连锁故障传播元件的脆弱性评估［J］. 电力系统自动化，2012，36（19）：11-16.LI Yong，LIU Junyong，LIU Xiaoyu，et al.Vulnerability assessment in power grid cascading failures based on entropy of power flow［J］.Automation of Electric Power Systems，2012，36（19）：11-16.

［13］谭玉东，李欣然，蔡晔，等.基于电气距离的复杂电网关键节点识别［J］. 中国电机工程学报，2014，34（1）：146-152.TAN Yudong，LI Xinran，CAI Ye，et al.Critical node identification for complex power grid based on electrical distance［J］.Proceedings of the CSEE，2014，34（1）：146-152.

［14］王涛，高成彬，顾雪平，等.基于功率介数的电网关键环节辩识［J］. 电网技术，2014，38（7）：1907-1913.WANG Tao，GAO Chengbin，GU Xueping，et al.Power betweenness based identification of power grid critical links［J］.Power System Technology，2014，38（7）：1907-1913.

［15］蔡晔，曹一家，李勇，等.考虑电压等级和运行状态的电网脆弱线路辩识［J］. 中国电机工程学报，2014，34（13）：2124-2131.CAI Ye，CAO Yijia，LI Yong，et al.Identification of vulnerable lines in urban power grid based on voltage grade and running state［J］.Proceedings of the CSEE，2014，34（13）：2124-2131.

［16］倪向萍，梅生伟，张雪敏.基于复杂网络理论的输电线路脆弱度评估方法［J］. 电力系统自动化，2008，32（4）：1-5.NIXiangping，MEIShengwei，ZHANG Xuemin.Transmission lines vulnerability assessment based on complex network theory［J］.Automation of Electric Power Systems，2008，32（4）：1-5.

［17］雷成，刘俊勇，魏震波，等.积极网络传导能力与抗干扰能力的节点综合脆弱评估模型［J］. 电力自动化设备，2014，34（7）：144-149.LEI Cheng，LIU Junyong，WEI Zhenbo，et al.Node integrative vulnerability evaluation model considering network transmission ability and anti-interference ability［J］.Electric Power Automation Equipment，2014，34（7）：144-149.

［18］CHEN J，THORP J S，DOBSON I.Cascading dynamics and mitigation assessment in power system disturbances via a hidden failure model［J］.Electrical Power and Energy Systems，2005，27（4）：318-326.

［19］陈丹宇.长三角区域创新系统中的协同效应研究［D］.杭州：浙江大学，2009.CHEN Danyu.Research on synergy effects in regional innovation systems of the Yangtze-Delta［D］.Hangzhou：Zhejiang University，2009.

［20］PAI M A.Energy function analysis for power system stability［M］.Boston，USA：Kluwer Academic Publishers，1989.