基于CLARA算法的考虑时序特性分布式电源规划

白晓清，赵 瞻，鲍海波

（广西大学 广西电力系统最优化与节能技术重点实验室，广西 南宁 530004）

0 引言

分布式电源 DG（Distributed Generator）在配电系统的大量接入，会引起电网结构、潮流分布的显著改变［1］。DG配置不合理不仅无法发挥其节能降损、改善电能质量的作用，还直接威胁电网安全［2］。作为分布式发电理想形式的光伏发电和风力发电，具备清洁、可再生等优点的同时，其出力也存在较强的随机性和间歇性［3］，从而加大了DG的规划难度。此外，不同类型DG出力还具有显著的时序特性，与负荷波动水平在时序上的匹配程度也不尽相同［4］。因而，更为全面地考虑DG出力特性，充分发挥其积极效益、抑制负面影响，成为科学规划DG安装位置及容量的关键。

针对DG规划问题，国内外专家学者已经进行了大量的研究工作。文献［5］在假定DG总接入容量已知、安装位置和各节点安装容量未知的情况下对其优化，不考虑风机等DG容量不可连续调节的特性，将其作为传统电源处理。文献［6］以配电网年费用最小为目标，应用遗传算法对DG的位置和容量进行优化。文献［7］提出一种基于“负荷质心”的DG优化配置方法。文献［8-11］提出了多目标DG选址、定容规划模型。以上研究基于DG出力以及负荷的某一静态时刻值，不计及出力波动性和时序特性对规划结果的影响。文献［12-14］考虑DG出力的极端场景，例如在DG出力最大/负荷最小或者DG出力最小/负荷最大的情形下对其安装位置及容量进行优化。文献［15-16］研究光伏电源的选址定容问题，在每个时段对光伏发电出力以及负荷建立多状态模型。文献［17-19］利用典型日的风、光量测数据绘制出DG出力时序特性曲线，并在此基础上对其进行规划，考虑了DG出力的时序特性，但未考虑其随机性。

基于上述分析，DG出力同时具备时序性和随机性。本文尝试同时考虑这2个特性，针对DG选址和定容问题，建立基于长时间序列的混合整数非线性随机规划模型，使得DG规划更为符合实际情况。计及风电、光电出力水平在时序上的差异，构造各时段风速以及太阳光照强度的概率分布，并利用蒙特卡洛模拟法生成描述全年DG出力情况的多个序列场景。通过IEEE 14和IEEE 33节点标准系统测试表明，考虑时序特性有利于发挥风、光资源的互补优势，提高DG出力与负荷水平在时序上的匹配程度，进而达到较好的降损效果。

将DG出力的时序特性引入到规划研究中往往会引起场景数目的大量增加，模型求解难度随之加大。文献［20-21］采用场景最优消减技术对原始场景进行压缩。文献［22］利用K-Mediods聚类算法对风功率序列场景进行缩减。这些方法虽然易于实现，但计算量会随着场景数目的增加而显著加大，难以缩减本文所提方法产生的基于时间跨度较长的大量序列场景。为了解决大量序列场景缩减计算困难的问题，本文利用改进的CLARA（Clustering LARge Application）算法［23］对描述每一场景各时段 DG出力及负荷波动水平的样本点进行聚类。改进的CLARA算法在传统算法的基础上引入K-Means方法选择类的初始中心点，避免传统方法中初始点选取的盲目性，能显著缩短计算时间；此外，借助三角形三边约束消除准则减少了归类过程中的重复计算，提高了计算效率。相比其他方法，该算法具有较强的鲁棒性，适用于大规模数据集的聚类问题。本文最后验证了该方法处理DG随机出力数据的适用性和有效性。该方法能够保证优化结果的近似误差在允许范围内的同时，显著减小模型的求解难度和计算时间。

1 DG出力模型

1.1 风机出力模型

经大量实测风速数据表明，风速变化规律服从Weibull分布［24］，本文采用曲线形状与实际情况匹配较好的Rayleigh分布（即k=2的Weibull分布）来描述风速的变化规律，分布函数为：

其中，v为风机叶轮轮毂风速；k为形状参数；c为尺度参数；UW为［0，1］区间均匀分布的随机数。参照文献［13］取 c=1.128 vm，vm是风速的平均值。 式（1）整理可得：

风机输出功率与风速之间的关系可近似用分段函数表达：

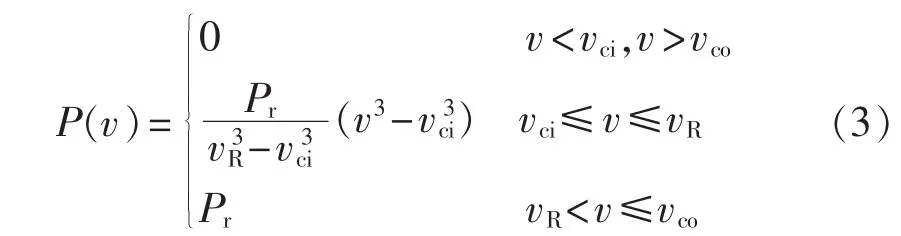
其中，P为风机输出功率；vci为切入风速；vR为额定风速；vco为切出风速；Pr为风机额定功率。联立式（2）和式（3）得：

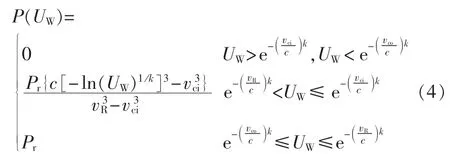
风机发生故障出现停运状态为随机事件［25］，Pfo为发生停运的概率，在［0，1］区间抽取均匀分布的随机数UR确定风机的运行状态，故考虑故障退出情况的出力模型为：

1.2 光伏电源出力模型

采用与实际太阳辐射情况拟合较好的Beta分布来描述各时段光照强度的变化规律［26］，式（6）为其概率密度函数。

其中，s为光照强度；α、β为Beta分布的参数。

光伏电源出力依赖于设备自身的实际特性、光照强度和周围环境的温度。已知光照强度、环境温度，可根据式（7）计算出光伏电源的实际输出功率。

其中，Tcy为光伏电源温度；TA为环境温度；say为该状态下的光照强度；NOT为设备的额定温度；Isc为额定短路电流；Uoc为额定开路电压；Iy、Uy分别为该状态下电源的短路电流及开路电压；Ki为短路电流温度系数；KU为开路电压温度系数；FF为太阳能电池的填充因数；UMPP、IMPP分别为光伏电源输出最大功率时的电压值与电流值；PSy为光伏电源实际输出功率。

1.3 DG的时序特性

风机及光伏电源出力具有显著的时序特性，伴随季节和时间变化有较大差异［18］。本文计及全年各时段风速以及光照强度水平的不同，以1 h为一个时段，分别采用概率密度分布对各时段风速及光照强度进行描述。由于同一季节相同时刻风速的平均水平基本相同，且影响风速的因素相差不大，可以认为这些时段的风速服从同一概率分布［27］。同样，相同时刻的光照强度也服从同一分布［28］。因此，全年每一季度的风速情况、光照强度可以分别用24个不同时段的概率分布进行描述，即全年共需96个不同时段的概率分布。收集某地区近3年风速的历史数据［29］，图1是该地96个不同时段风速的概率密度曲线，图2是各对应时段风速的平均值及标准差。

图1 96个不同时段风速概率密度曲线Fig.1 PDF curve for 96 periods

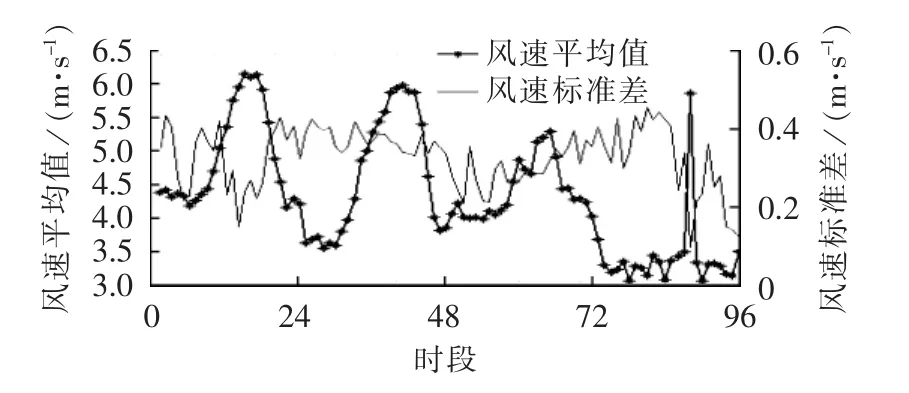
图2 对应时段风速平均值及标准差Fig.2 Mean and standard variation of wind speed for 96 periods

由图可看出，不同季节不同时段风速的概率密度分布曲线有较大差异，平均水平也各不相同，验证了考虑时序特性对真实反映风速变化规律的必要性。另外，根据同一时段风速的标准差数值较小可判断其离散程度较小，表明同季节同时段风速水平相差不大，特征相近，可利用同一分布描述。该结论对光照数据同样适用，此处不再赘述。

2 DG规划模型

2.1 随机规划数学模型

考虑出力波动性的DG规划问题是一个包含随机变量、多变量、多约束的随机优化问题。寻求随机环境下极小化目标问题可通过如下模型表示：

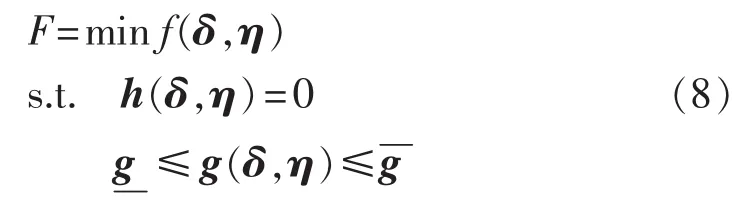
其中，δ为概率分布已知的随机向量；η为决策变量；f（δ，η）为目标函数；h（δ，η）、g（δ，η）分别为等式约束和不等式约束。

2.2 基于聚类缩减模型的多场景多时段DG规划

随机规划问题的求解需要对随机变量进行详细描述，可利用随机变量的离散概率分布近似表达其连续概率分布，进而将随机优化问题转化为确定性优化问题。可以采用场景法［30］实现该方法。通过获取随机变量δ的离散场景，将随机规划模型式（8）转换为基于抽样场景的确定性优化模型。

蒙特卡洛模拟是获取随机变量离散场景的有效方法［31］，模拟次数越多，仿真结果越准确。 文献［32］验证对风速经过5000次蒙特卡洛模拟，仿真结果趋于稳定。本文生成描述全年DG出力及负荷水平的100个全场景，各场景相同时段采样次数90次，则每时段有9 000次蒙特卡洛模拟，可满足模拟精度要求。

然而，使用混合整数规划方法求解本文基于蒙特卡洛仿真的随机模型时，随着仿真次数的增多，求解时间将呈指数形式上升［33］。因此，将上述所提方法产生的全部场景直接耦合形成全场景模型，会造成问题的规模过大、求解困难。

聚类分析是研究如何将对象按照多个特性进行综合分类的一种统计方法，它根据对象相似程度进行分类，使同类对象在某些性质上最为相近［34］。通过聚类确定质量最佳的归类方案，并由中心点代表整个类的随机变量水平。本文将全场景归入各自的代表类中，把对全场景模型的求解问题转化为基于类的求解，将对所有场景的约束转换为基于类的约束，提出聚类缩减模型。其求解难度与类的个数相关，类的个数一经确定求解难度不会随着场景数目的增加而加大。建立目标函数为：

其中，第a类中心点对应的能量损耗用Plossa表示，共计 A 个类，表示为向量［Ploss］A×1，即［Ploss］A×1=［Ploss1，…，Plossa，…，PlossA］T；Ny为场景数；［Lj］用来描述第 j个场景各时段DG出力及负荷波动水平归属的类，包含有8640个行向量lline，依次描述1—8640时段随机状况归属类的情况，每一行向量均有A-1个0元素、1个1元素，1元素所在位置对应于该时段所属的类，例如某场景第i时段从属于第1个类，即有描述该时段的行向量为［1，0，0，…］，对应的损耗值为Ploss1。

所需满足的约束条件为：

其中，bi、ni分别为风机、光伏电源安装位置的0、1变量；wi、ri为安装组数的整数变量；和分别为类s表征状态下节点i处常规电源的有功和无功出力；和分别为其有功和无功负荷；和分别为该状态下节点i处单位风机、光伏电源的实际出力。式（12）表述了各节点安装DG的组数约束。

其中，Umin为节点电压的下限；Umax为节点电压的上限；Prw和Prs分别为单位风机以及单位光伏电源的额定功率；MB和MN分别为风机以及光伏电源总布点个数的最大限制。式（15）为DG接入容量的最大限制，认为接入总容量不得超过常规电源出力的γ1倍与负荷的γ2倍之和，实际应用中可以根据当地政策的限制对倍数进行调整。

2.3 考虑时序特性的多场景模拟

假定各季度均为90 d，全年共计8640 h。依照时间序列，用蒙特卡洛法对风速以及光照强度进行概率抽样。采样间隔为1 h，各场景以1—8640时段为一时间序列，生成考虑时序特性的多个场景。同场景同一时段的风速以及光照强度由［0，1］区间内同一随机数代入各自概率分布的反函数求解得到。其流程见图3。

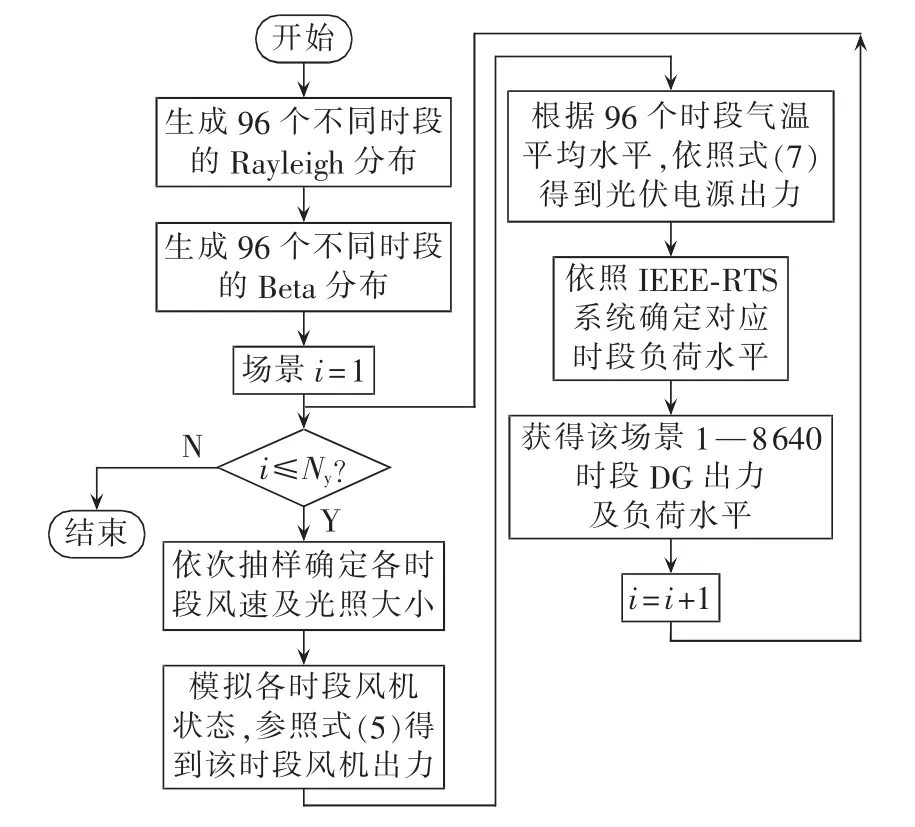
图3 场景生成流程图Fig.3 Flowchat of scene generation

3 基于CLARA聚类的场景处理

3.1 基本思路

目前被用于解决场景缩减的聚类方法一般有K-Means算法、K-Medoids算法和基于这2种算法的改进算法［35］。 文献［36-37］利用 K-Means 算法对描述DG出力及负荷不确定性的场景进行缩减。PAM（Partitioning Around Medoids）是 K-Medoids 算法的一种，区别于K-Means等算法，该方法的中心点为数据集中的数据，有效消除了离群点对聚类效果的影响，具有较强的鲁棒性和较高的准确性［38］。但其时间复杂度高，难以解决大规模数据的聚类问题。为了能够处理大规模数据集的聚类问题，Kaufmann和Rousseeuw在PAM方法基础上添加了抽样思想，提出了有效的CLARA聚类法［39］。

CLARA算法的基本思想为对原始样本进行随机抽样，通过抽取部分数据来代表整体数据。然后利用PAM算法进行聚类，反复用非代表对象替换代表对象，通过代价函数确定好的替换方式以及质量最佳的聚类方案。为了减少样本偏斜对聚类结果产生的影响，CLARA算法对原始数据进行多次抽取，重复聚类过程，并选择效果最优的方案。

CLARA算法采用抽样的思想可降低数据规模。当采样方式完全随机且抽样规模达到一定要求时，抽取后的数据能够在允许偏差范围内还原原始数据信息［23］。针对间歇性较强的分布式电源出力数据，CLARA算法同样适用，在本文算例分析中将对其适应性做进一步检验。

描述风机、光伏电源出力水平以及负荷水平的采样点可以看作三维空间中的向量，如图4所示，利用欧氏距离表示任意2点x和y之间的距离，即：

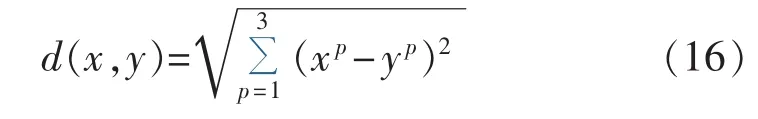
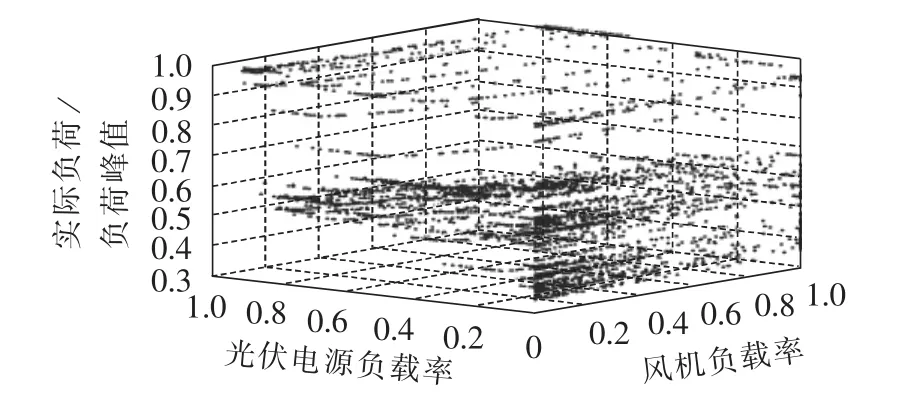
图4 各时段DG出力及负荷波动水平分布Fig.4 Distribution of DG output and load fluctuation in a period

非中心点替换中心点时，利用代价函数判断该替换是否能够改善聚类质量；以xh替代xi时，根据式（17）可得代价函数：

其中，cjih为xh替换xi时非代表点xj的替换代价，其取值分以下2种情况讨论，其中记xj，sub为xj的次近中心点。

a.xj属于 xi存在的一类，当 d（xj，xh）＜d（xj，xj，sub）时，cjih=d（xj，xh）-d（xj，xi），否则，cjih=d（xj，xj，sub）-d （xj， xi） 。

b.xj属于中心点为 xl（l≠i）的一类，当 d（xj，xl）＜d（xj，xh）时，cjih=0；否则，cjih=d（xj，xh）-d（xj，xl）。

替换代价数值为负表明执行该替换有利于聚类质量的提高，反之，并非为有利的替换。

3.2 实现步骤

3.2.1 三角形三边约束消除准则

PAM算法耗时的关键在于反复地在非中心点与中心点之间进行搜索和替换，进而产生大量的重复计算。本文对传统算法进行改进，利用三角形三边之间的距离约束关系消除部分计算，从而有效降低了计算的复杂度。

已知满足距离约束关系：

假如：

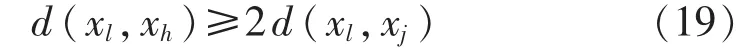
则有：

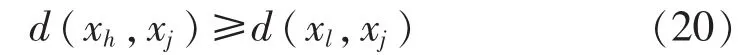
若满足式（19），即点xj与其中心点xl的距离不足xl与替换点xh距离的一半时，可直接判断点xj离xl更近。 d（xl，xh）与 d（xl，xj）在前面的步骤中已计算并保存，利用该准则可省去d（xh，xj）的计算，减少了计算量。

3.2.2 具体步骤

采用改进CLARA算法聚类的一般步骤如下。

（1）对于 t=1，2，…，96（即对各时段采样点分别进行聚类），重复执行下列步骤。

（2）对于 i=1，2，…，V（V 取值为 10，即为减小抽样偏差，重复聚类的次数），重复步骤（3）—（5），选择质量最好的聚类方案代入规划模型中计算。

（3）从t时段不确定变量的数据集中随机抽取样本，将聚类规模降至原来的1/M，由此形成包含N个对象的样本。

（4）利用K-Means算法获得样本的粗糙中心，取样本数据中距离粗糙中心最近的数据作为初始中心，将非中心点归入距离最近中心点所在类中。

（5）计算每一个非中心点替换中心点的代价，利用三角形三边约束消除准则减小计算量。执行代价为负值且绝对值最大的替换，并形成新的中心点集以及新的分类。重复替换直到全部代价均为非负值为止。

本文利用总误差对聚类质量进行度量，即为所有非代表对象与其代表对象的距离之和，如式（21）所示。

其中，xi为非代表对象；xi，dep为其所属类的代表对象。总误差数值越小，表明聚类效果越佳。

4 算例分析

4.1 参数设置及算例设计

系统参数设置为：停运状态发生概率Pfo=0.005，模拟全年情况的场景数Ny=100，接入点安装风机最小组数wmin=1，最大组数wmax=200，接入点安装光伏电源最小组数rmin=1，最大组数rmax=200，风机单位机组的额定功率Prw=0.01 MW，光伏电源单位机组额定功率Prs=0.01 MW。风机、光伏电源布点之和最大值分别为MB=5、MN=5。当接入风、光发电设备时，γ1=0.6，γ2=0.3；当仅接入风力发电设备或光伏发电设备时，γ1=0.3，γ2=0.15，基准值为 100 MW。

每一场景共有模拟点8640个，相同季节相同时段的样本个数为8640/96=90，计及多场景，各时段样本9000个。M=3，N=3 000，分别聚为10类，总计 A=96×10=960。

选取IEEE14和IEEE33节点标准系统验证本文模型的正确性以及改进CLARA算法的有效性，测试算例如表1所示。

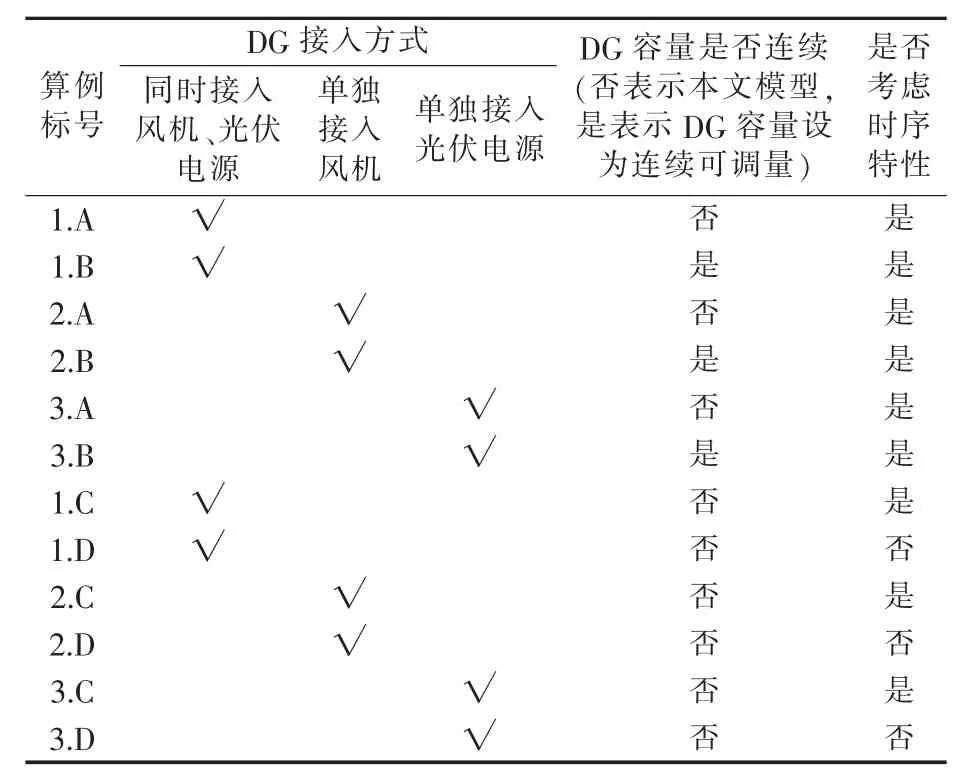
表1 测试算例Table 1 Test cases

4.2 DG接入影响

考虑IEEE 14节点标准系统的DG选址定容，表2为各算例的优化策略及损耗（标幺值，后同）对比。由于DG实际容量不连续可调，本文模型在利用0-1变量表达其布点位置的同时，引入整数变量描述其配置容量。由表2可以看出，本文模型与将DG安装容量视为连续可调量模型相比，降损效益损失低于1%。即本文模型能同时兼顾系统实际情况和经济效益。

表2 优化策略及损耗对比Table 2 Comparison of optimization strategy and power loss among cases

节点8、9负荷较重，分别占整个系统总负荷的17.4%、15.68%。表2结果显示，各类型DG均会选择在这2个负荷较重的节点处接入，进而有效地实现重负荷的就地平衡，减少功率流动，降低配电网损耗。图5展示单独接入风机、光伏电源以及同时接入这2种类型DG时，本文模型优化配置下的系统损耗与无DG系统的损耗（标幺值）对比。不接入DG时，损耗电量为17.768p.u.，接入DG后系统损耗得到显著降低。

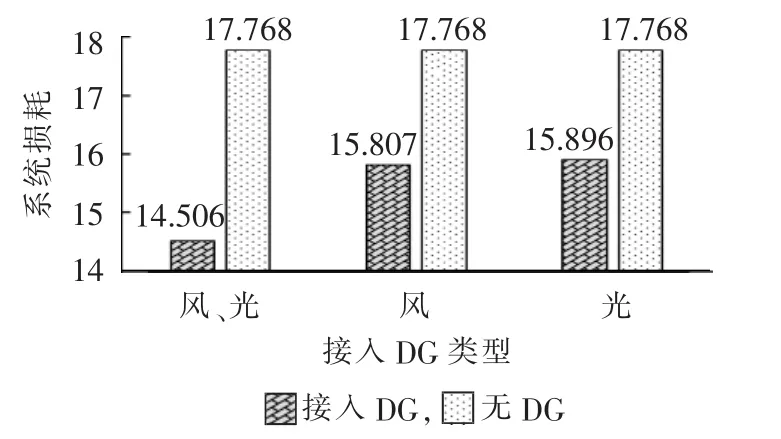
图5 DG接入前后系统损耗对比Fig.5 Comparison of power loss between with and without DGs

图6展示风机实际出力占额定功率81.42%、光伏电源出力为额定功率21.05%、负荷波动为峰值的64%时配电网络各节点电压的分布情况（图中电压幅值为标幺值）。可见，DG接入配电网，电压水平得到提高，其中以DG接入点的电压升高最为显著。DG的接入能够有效减小馈线上的传输功率，抬升过低电压，提高电压水平。

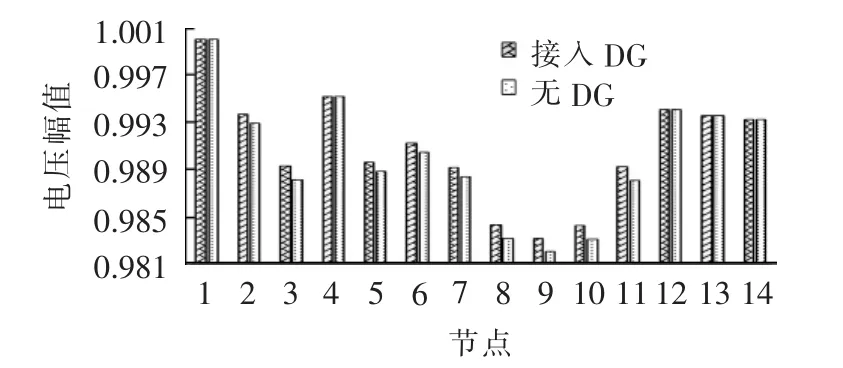
图6 各节点电压分布情况Fig.6 Comparison of node voltage distribution between with and without DGs

为了进一步验证本文模型与方法，以文献［40］提供的33节点配电网为算例，对DG布点及容量配置进行优化，优化结果如表3所示，表中损耗为标幺值，后同。该系统与 IEEE 14节点系统相比，负荷较轻，DG投入量小，但降损效益显著，达19.26%。结果表明，该模型对求解轻负荷系统的DG优化配置问题同样具有较好的效果。

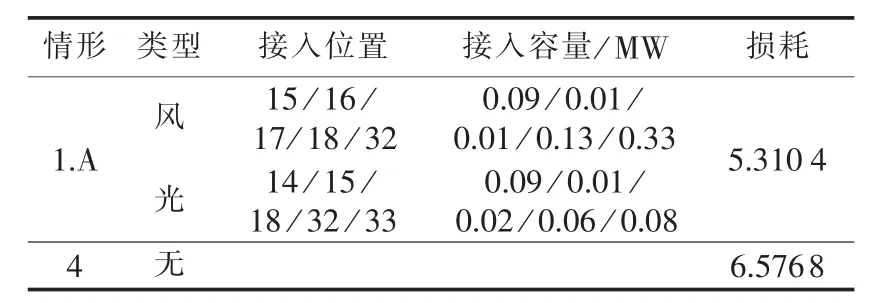
表3 33节点系统DG优化策略Table 3 DG optimizaiton strategy of 33-bus system

4.3 时序特性的影响

为了展示DG出力及负荷的时序特性对规划结果的显著影响，本节采用随机排列生成风机以及光伏电源出力水平的顺序以产生忽略时序特性的DG出力算例，并与前述考虑时序特性的DG出力算例的结果进行比较。表4分别为考虑以及忽略时序特性时DG的配置方案。

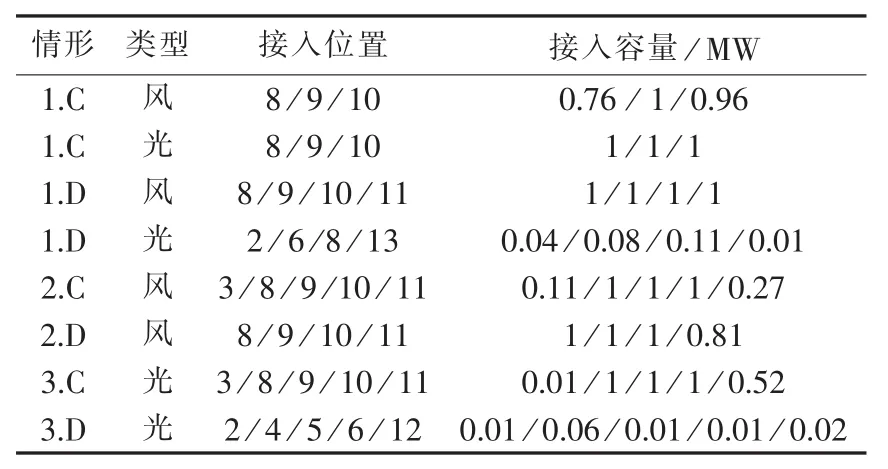
表4 考虑与忽略时序特性时DG配置方案Table 4 Comparison of DG planning among cases with and without consideration of timing-series characteristics

不考虑时序特性时，风、光发电除了效率以外无差别，从表2结果可知，较风力发电，光伏发电利用率稍低。如表4所示，忽略时序特性同时引入风、光发电设备时，光伏电源引入比重较小，效率较高的风电设备得到了优先投入；考虑时序特性后，基于风、光资源在时序上的互补作用，风力较弱时，光伏发电是风力发电的有益补充，投入量得到增加。忽略时序特性会造成风、光机组组合出力水平在数值上与实际情况偏差较大，导致规划结果不准确。另外，由考虑时序特性以及忽略时序特性时DG配置结果对比可知，考虑时序特性有利于发挥风、光资源在时序上的互补作用，提高对自然资源的利用率。

图7分别展示了无DG接入、单独接入风机、单独接入光伏电源以及同时接入上述2种设备时各季节每一时段的损耗电量。其中，每时段损耗电量为该季节共计90 d相同时段损耗电量之和，共展示96个不同时段。

图7 1—96时段各时段配电网损耗电量Fig.7 Power losses for 96 periods

各时段电量的损耗情况充分表明了风机以及光伏电源出力在时序上的互补优势。以1—24时段曲线为例，该时段展示了春季各时段的电量损耗。其中，01∶00—05∶00 光照强度为 0，当仅考虑接入光伏电源时，其损耗曲线与不接入DG的损耗曲线相吻合；08∶00—13∶00，风力较弱，光照相对较强，该时段内，光伏发电的作用较为显著，接入风机情形下的电量损耗高于接入光伏电源；之后光照变弱，风力较强，风力发电的降损效果更为显著。同时接入风、光2种发电设备，可以有效弥补独立发电的不足，达到较好的降损效益。

4.4 CLARA有效性测试

选择IEEE 14节点标准系统，通过对比将全部场景直接代入模型联立计算的结果，验证本文所提改进CLARA算法的有效性。该算例中，场景数为1，改变每一相同时段的模拟点数，分别通过36次、72次等次数的概率抽样模拟对应时段的随机变量。2种场景处理方法下模型的求解情况如表5所示，其中，近似误差为以上2种处理方法所得损耗差值与全场景代入所得结果百分比；提速比为全场景法耗时大小与CLARA算法耗时大小之比。设置3000 min为阈值，求解时间超过该阈值则认为该方法失效。

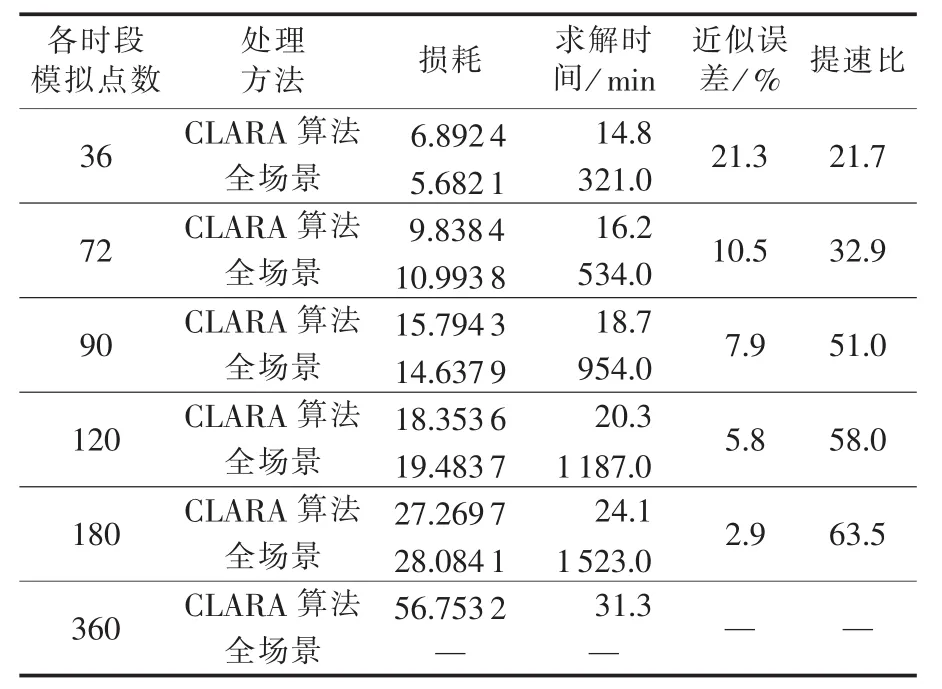
表5 CLARA聚类与直接代入结果对比Table 5 Comparison between CLARA clustering and direct method

由表5知，采样点数量较少时，2种处理方法下优化结果差异较大；随着原始数据规模不断变大，利用CLARA算法聚类与将全部场景直接代入模型计算的结果相比，近似误差不断缩小。单场景单时段采样点个数为180时，近似误差不超过3%，根据趋势可推论，本文场景数为100时，利用CLARA算法得到的结果与全场景优化效果将会更为逼近。此外，随着计算规模的扩大，求解时间增加缓慢，有效解决为提高模拟精度增加仿真次数时，全场景直接代入模型将出现求解时间过长或者模型不可求解的问题。

本文计及多场景，利用CLARA算法聚类先将描述各时段分布式电源出力的采样点由9000个降至3000个，为验证对于间歇性较强的数据，抽样后得到的部分数据仍能有效还原原始样本信息，采用均值、方差、偏度和峰度作为衡量指标进行说明。图8为96个时段随机抽取后得到的样本与原始样本4个数字特征指标的百分比堆积柱形图。曲线以下部分代表随机抽取后所得样本所占比例，上部分代表原始样本所占比例，曲线代表两者之间的差异，波动越为平缓，差异越小，波动越大，差异越大。由图8可知，各个时段两者差异较小，相当程度上说明，随机抽取得到的数据能够较好地保留原始数据的特征，验证了CLARA算法适用于解决不确定性较强的分布式电源出力数据的聚类问题。

为了进一步验证较PAM算法，CLARA算法抽取的样本能够反映原始样本的数据信息，引入采用PAM聚类的优化结果进行对比。设定场景数为100，通过改变各时段的模拟点数进行对比计算，如表6所示，近似误差为2种算法所得损耗差值与PAM算法所得结果的百分比，设置50 h（3000 min）为阈值，超过该阈值认为该方法失效。

据表6可知，2种聚类方法处理下优化结果相差不大。随着采样点规模的扩大，CLARA算法得到的优化结果与PAM算法不断逼近，近似误差不足1%，表明随机抽取的数据能较为完整地还原初始数据的信息，CLARA算法对解决不确定性数据的聚类问题行之有效。当数据规模较大，原有的PAM算法因为执行时间过长而不再适用时，CLARA算法仍能在相对较短的时间内完成计算。该方法适于解决大规模数据的聚类问题，能有效克服仿真次数增多模型求解难的问题，对工程实践有较好的使用价值。

图8 统计特征对比图Fig.8 Comparison of statistical indexes

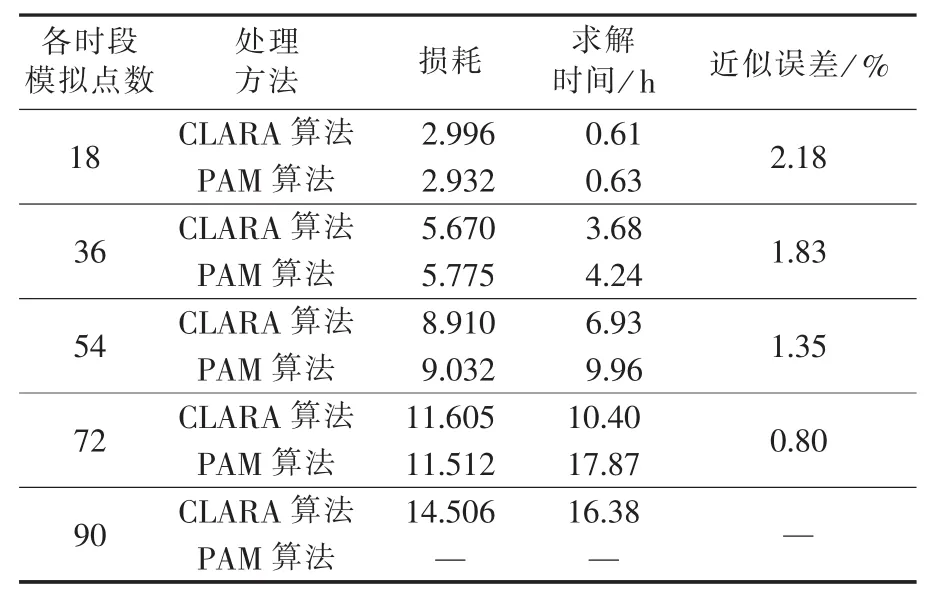
表6 CLARA聚类与PAM聚类结果对比Table 6 Comparison between CLARA clustering and PAM clustering

5 结论及展望

本文基于负荷以及DG出力的时序特性，建立以年损耗电量最小为目标的多场景多时段DG规划模型，并在GAMS环境下进行建模。结果表明：

（1）考虑DG出力的时序特性，能够更为真实地反映系统的运行情况，得到的规划方案也更具有实际意义；

（2）太阳能与风能在时序上具有互补优势，这2种DG同时接入可以弥补风力发电或光伏发电独立系统的缺陷；

（3）利用改进CLARA算法对各时段随机模拟量进行聚类，在保证优化结果近似误差较小的同时有效降低了模型的计算量，该方法对工程实践有较好的实用价值。

本文所提改进的CLARA算法对处理大规模DG出力随机样本的缩减问题具有通用性。针对DG随机规划问题，下一步研究将着重目标函数多样化，如考虑系统总成本最小化、投资净收益最小化、系统供电可靠性最大化、单位电能成本最小化等。

［1］栗然，马慧卓，祝晋尧，等.分布式电源接入配电网多目标优化规划［J］. 电力自动化设备，2014，34（1）：6-13.LI Ran，MA Huizhuo，ZHU Jinyao，et al.Multi-objective optimization for DG integration into distribution system ［J］.Electric Power Automation Equipment，2014，34（1）：6-13.

［2］文升，顾洁，程浩忠，等.分布式电源的准入容量与优化布置的实用方法［J］. 电力自动化设备，2012，32（10）：109-114.WEN Sheng，GU Jie，CHENG Haozhong，et al.Maximum penetration level and optimal placement of distributed generation［J］.Electric Power Automation Equipment，2012，32（10）：109-114.

［3］徐林，阮新波，张步涵，等.风光蓄互补发电系统容量的改进优化配置方法［J］. 中国电机工程学报，2012，32（25）：88-98.XU Lin，RUAN Xinbo，ZHANG Buhan，etal.An improved optimal sizing method for wind-solar-battery hybrid power system［J］.Proceedings of the CSEE，2012，32（25）：88-98.

［4］丁明，王伟胜，王秀丽，等.大规模光伏发电对电力系统影响综述［J］. 中国电机工程学报，2014，34（1）：1-14.DING Ming，WANG Weisheng，WANG Xiuli，et al.A review on the effect of large-scale PV generation on power systems ［J］.Proceedings of the CSEE，2014，34（1）：1-14.

［5］RAU N S，WAN Y H.Optimum location of resources in distributed planning［J］.IEEE Transactions on Power Systems，1994，9（4）：2014-2020.

［6］王成山，陈恺，谢莹华，等.配电网扩展规划中分布式电源的选址和定容［J］. 电力系统自动化，2006，30（3）：38-43.WANG Chengshan，CHEN Kai，XIE Yinghua，et al.Siting and sizing of distributed generation in distribution network expansion planning［J］.Automation of Electric Power Systems，2006，30（3）：38-43.

［7］唐小波，徐青山，唐国庆.基于“负荷质心”的分布式电源并网优化配置［J］. 电力自动化设备，2011，31（2）：12-16.TANG Xiaobo，XU Qingshan，TANG Guoqing.Optimal configuration based on load centroid for distributed generation grid-connection［J］.Electric Power Automation Equipment，2011，31（2）：12-16.

［8］WANG Caisheng，NEHRIR M H.Analyticalapproachesfor optimal placement of distributed generation sources in power systems［J］.IEEE Transactions on Power Systems，2004，19（4）：2068-2076.

［9］王瑞琪，李珂，张承慧，等.基于多目标混沌量子遗传算法的分布式电源规划［J］. 电网技术，2011，35（12）：183-189.WANG Ruiqi，LI Ke，ZHANG Chenghui，et al.Distributed generation planning based on multi-objective chaotic quantum genetic algorithm［J］.Power System Technology，2011，35（12）：183-189.

［10］曾鸣，杜楠，张鲲，等.基于多目标静态模糊模型的分布式电源规划［J］. 电网技术，2013，37（4）：954-959.ZENG Ming，DU Nan，ZHANG Kun，et al.Distributed generation planning based on multiobjective static fuzzy model［J］.Power System Technology，2013，37（4）：954-959.

［11］栗然，申雪，钟超，等.考虑环境效益的分布式电源多目标规划［J］. 电网技术，2014，38（6）：1471-1478.LI Ran，SHEN Xue，ZHONG Chao，et al.Multi-objective planning of distributed generation considering environmental benefit［J］.Power System Technology，2014，38（6）：1471-1478.

［12］ATWA Y M.Optimal renewable resources mix for distribution system energy loss minimization［J］.IEEE Transactions on Power Systems，2010，25（1）：360-370.

［13］ALABRIRS，EL-SAADANYEF，ATWAYM.Optimal placement and sizing method to improve the voltage stability margin in a distribution system using distributed generation［J］.IEEE Transactions on Power Systems，2013，28（1）：326-334.

［14］唐念，夏明超，肖伟栋，等.考虑多种分布式电源及其随机特性的配电网多目标扩展规划［J］.电力系统自动化，2015，39（8）：45-52.TANG Nian，XIA Mingchao，XIAO Weidong，et al.Multi-objective expansion planning of active distribution systems considering distributed generator types and uncertainties［J］.Automation of Electric Power Systems，2015，39（8）：45-52.

［15］张璐，唐巍，丛鹏伟，等.含光伏发电的配电网有功无功资源综合优化配置［J］. 中国电机工程学报，2014，34（31）：5525-5533.ZHANG Lu，TANG Wei，CONG Pengwei，et al.Optimal configuration of active-reactive power sources in distribution network with photovoltaic generation［J］.Proceedings of the CSEE，2014，34（31）：5525-5533.

［16］LI Ruihuan，GAO Yajing，CHENG Huaxin.Two step optimal dispatch based on multiple scenarios technique foractive distribution system with the uncertainties of intermittent distributed generation and load considered［C］∥2014 International Conference on Power System Technology.Chengdu，China：IEEE，2014：3303-3308.

［17］段建民，王志新，王承民，等.考虑碳减排效益的可再生能源规划［J］. 电网技术，2015，39（1）：11-15.DUAN Jianmin，WANG Zhixin，WANG Chengmin，et al.Renewable power planning considering carbon emission reduction benefits［J］.Power System Technology，2015，39（1）：11-15.

［18］徐迅，陈楷，龙禹，等.考虑环境成本和时序特性的微网多类型分布式电源选址定容规划［J］. 电网技术，2013，37（4）：914-921.XU Xun，CHEN Kai，LONG Yu，et al.Optimal site selection and capacity determination of multi-types of distributed generation in microgrid considering environment cost and timing characteristics［J］.Power System Technology，2013，37（4）：914-921.

［19］赵渊，何媛，宿晓岚，等.分布式电源对配网可靠性的影响及优化配置［J］. 电力自动化设备，2014，34（9）：13-20.ZHAO Yuan，HE Yuan，SU Xiaolan，et al.Effect of distributed generation on powerdistribution system reliability and its optimal allocation［J］.Electric PowerAutomation Equipment，2014，34（9）：13-20.

［20］DUPACOVA J，GROWE K N，ROMISH W.Scenario reduction in stochastic programming an approach using probability metrics［J］.Math Program，2003，95：493-511.

［21］RAZALI N M M，HASHIM A H.Backward reduction application for minimizing wind power scenarios in stochastic programming［C］∥Power Engineeringand Optimization Conference，2010 4th International.Shah Alam，Malaysia：IEEE，2010：430-434.

［22］SUMALILI J，KEKO H，MIRANDA V.Clustering-based wind power scenario reduction technique［C］∥17th Power System Computation Conference.Stockholm，Sweden：PSCC，2011：653-658.

［23］TAN Pangning，STEINBACH M，KUMAR V.Introduction to date mining［M］.Boston，USA：Pearson Addison Wesley，2006：231-252.

［24］苏小玲，韩民晓，赵正奎，等.配电网中分布式电源最大准入容量分析［J］. 电网技术，2012，36（10）：87-92.SU Xiaoling，HAN Minxiao，ZHAO Zhengkui，et al.Research on maximum capacity of grid-connected distributed generation in distributed network［J］.Power System Technology，2012，36（10）：87-92.

［25］汪海瑛，白晓民，许婧.考虑风光储协调运行的可靠性评估［J］.中国电机工程学报，2012，32（13）：13-20.WANG Haiying，BAI Xiaomin，XU Jing.Reliability assessment considering the coordination of wind power，solar energy and energy storage［J］.Proceedings of the CSEE，2012，32（13）：13-20.

［26］ATWA Y M，EL-SAADANY E F，SALAMA M M A，et al.Optimal renewable resources mix for distribution system energy loss minimization［J］.IEEE Transactions on Power Systems，2010，25（1）：360-370.

［27］李亮，唐巍，白牧可，等.考虑时序特性的多目标分布式电源选址定容规划［J］. 电力系统自动化，2013，37（3）：58-63.LI Liang，TANG Wei，BAI Muke，et al.Multi-objective locating and sizing of distributed generators based on time-sequence characteristics［J］.Automation of Electric Power Systems，2013，37（3）：58-63.

［28］陈丽，张晋国，苏海锋.考虑并网光伏电源出力时序特性的配电网无功规划［J］. 电工技术学报，2014，29（12）：120-127.CHEN Li，ZHANG Jinguo，SU Haifeng.Reactive power planning for distribution system with grid-connected photovoltaic system considering time-sequence characteristics［J］.Transactions of China Electrotechnical Society，2014，29（12）：120-127.

［29］Historical Data.Western regional climate center［EB/OL］. ［2014-11-23］.http：∥www.wrcc.dri.edu/.

［30］叶荣，陈皓勇，王钢，等.多风电场并网时安全约束机组组合的混合整数规划解法［J］. 电力系统自动化，2010，34（5）：29-33.YE Rong，CHEN Haoyong，WANG Gang，et al.A mixed integer programming method for security-constrained unit commitment with multiple wind farms［J］.Automation of Electric Power Systems，2010，34（5）：29-33.

［31］黎静华，韦化，莫东.含风电场最优潮流的Wait-and-See模型与最优渐近场景分析［J］. 中国电机工程学报，2012，32（22）：15-23.LI Jinghua，WEI Hua，MO Dong. Asymptotically optimal scenario analysis and Wait-and-See model for optimal power flow with wind power［J］.Proceedings of the CSEE，2012，32（22）：15-23.

［32］鲍海波，韦化.考虑风电的电压稳定概率评估的随机响应面法［J］. 中国电机工程学报，2012，32（13）：77-85.BAO Haibo，WEI Hua.A stochastic response surface method for probabilistic evaluation of the voltage stability considering wind power［J］.Proceedings of the CSEE，2012，32（13）：77-85.

［33］BIXBY E R，FENELON M，GU Zonghao，et al.MIP：theory and practice-closing the gap［M］.Boston，USA：Springer，2000：332-335.

［34］孙吉贵，刘杰，赵连宇. 聚类算法研究［J］. 软件学报，2008，19（1）：48-61.SUN Jigui，LI Jie，ZHAO Lianyu.Clustering algorithms research［J］.Journal of Software，2008，19（1）：48-61.

［35］韩忠明，陈妮，乐嘉锦，等.面向热点话题时间序列的有效聚类算法研究［J］. 计算机学报，2012，35（11）：2337-2347.HAN Zhongming，CHEN Ni，LE Jiajin，et al.An efficient and effective clustering algorithm for time series of hot topics［J］.Chinese Journal of Computers，2012，35（11）：2337-2347.

［36］彭春华，于蓉，孙惠娟，等.基于K-均值聚类多场景时序特性分析的分布式电源多目标规划［J］.电力自动化设备，2015，35（10）：58-65.PENG Chunhua，YU Rong，SUN Huijuan.Multi-objective DG planning based on K-means clustering and multi-scenario timing characteristic analysis［J］.Electric Power Automation Equipment，2015，35（10）：58-65.

［37］张沈习，李珂，程浩忠，等.间歇性分布式电源在主动配电网中的优化配置［J］. 电力自动化设备，2015，35（11）：45-51.ZHANG Shenxi，LI Ke，CHENG Haozhong，et al. Optimal allocation of intermittent distributed generator in active distribution network［J］.Electric Power Automation Equipment，2015，35（11）：45-51.

［38］张敏，于剑.基于划分的模糊聚类算法［J］. 软件学报，2004，15（6）：858-868.ZHANG Min，YU Jian.Fuzzy partitional clustering algorithms［J］.Journal of Software，2004，15（6）：858-868.

［39］RAYMOND T N，HAN J.Efficientand effectiveclustering methods for spatial data mining［C］∥Proceeding of the 20th VLDB Conference Santiago.San Francisco，USA：Morgan Kaufmann Publishers Inc，1994：144-155.

［40］PINHEIRO J M S，DORNELLAS C R R，SCHILLING M T，et al.Probing the new IEEE Reliability Test System （RTS-96）：HL-Ⅱ assessment［J］.IEEE Transactions on Power Systems，1998，13（1）：171-176.