考虑背景谐波波动的谐波责任划分方法

陈 静，符 玲，臧天磊，何正友

（西南交通大学 电气工程学院，四川 成都 610031）

0 引言

越来越多的电弧炉、换流器等非线性设备接入电网，给电网注入了大量的谐波［1-2］，引起电压畸变，导致电网的电能质量日益恶化，很大程度上影响了电网的优质运行。供电部门为了能向用户提供可靠优质的电能，针对谐波污染问题首先需要辨识出谐波源［3］并划分其谐波责任，以此来对谐波源用户进行惩罚［4］。

目前，国内外对谐波责任划分的研究主要是针对谐波阻抗和背景谐波电压的计算方法，其中很多是基于波动量法和线性回归法的优化［5-11］。这些方法大多是基于背景谐波不变的假设，而实际电网中的谐波参数是随时间变化的，故此类方法不能完全适应实际电网中的工况，因此，迫切需要开展适应背景谐波波动的谐波责任划分研究。

谐波责任划分的前提是正确估计背景谐波阻抗。由于在背景谐波波动工况下，用户侧和系统侧的谐波波动都比较剧烈，回归分析法适用于二者波动都较小的情况［9，12］，而波动量法在此工况下对背景谐波阻抗的估计更为准确。但传统的波动量法不能抑制背景谐波波动的影响［5-6］，而文献［5］中提出的主导波动量法由于充分考虑了背景谐波的波动，能够比较准确地在背景谐波变化情况下估计背景谐波阻抗，因而被后来的很多文献［11，13-14］借鉴使用。因此，为保证后续责任划分计算的准确性，本文同样采用主导波动量法进行背景谐波波动情况下的背景谐波阻抗的计算，即首先筛选出用户起主导作用的波动量来估计背景谐波阻抗，并在此前提下进行谐波责任的划分。

在谐波责任划分中，现有方法大多是基于谐波责任的定义式，用测得的谐波电压和谐波电流多个样本点的平均值计算得到谐波责任［7，9，15-16］，但是背景谐波波动情况下谐波电压和电流的波动都较大，现有方法的计算结果可能偏差较大，而且不能反映谐波电压和谐波电流的变化特征，无法消除背景谐波波动带来的影响。因此，为了利用背景谐波的波动并消除计算偏差，本文采用分位数回归法［17］划分用户的谐波责任。相比于常规回归方法，分位数回归法稳健性更好，数据信息的使用率更高，能够更好地估计背景谐波波动情况下用户的谐波责任。

基于上述分析，本文充分考虑背景谐波波动对谐波责任划分的影响，采用主导波动量筛选法和分位数回归法相结合的方法来划分用户谐波责任。首先建立了谐波责任的评价指标，然后简要介绍了采用主导波动量法求解背景谐波阻抗的原理，重点介绍了基于分位数回归法估计用户谐波责任的原理。为验证提出方法的准确性和适应性，在IEEE 13节点系统中进行了仿真分析，并与传统方法进行了比较。

1 谐波责任评价指标

谐波责任划分的关键是建立用于评价谐波责任的指标。在不同的电压等级下，相同的谐波电流对公共连接点的谐波责任不同，因此一般不采用谐波电流进行谐波责任划分，在工程实际中一般采用谐波电压作为评价谐波责任的重要指标。

关注母线处负荷接入模型如图1所示。关注母线X两侧分别为系统侧和用户侧。假设用户侧负荷C为主要谐波源，计算负荷C在所关注的母线X处产生的谐波责任。

以h次谐波为例，假设母线X的h次谐波电压为 UXh，负荷 C在母线 X处产生的谐波电流为ICh。根据叠加原理，母线处谐波电压UXh等于负荷C在母线X处产生的谐波电压UCh与系统其他谐波源产生的谐波电压U0h的叠加，即：

图1 关注母线处负荷接入模型Fig.1 Load connection model of concerned bus

其中，Zh为除负荷C外的系统侧与其他负荷的等效谐波阻抗；U0h为母线X处的背景谐波电压。用相量图表示如图2所示。

图2 母线X处谐波电压相量图Fig.2 Phasor diagram of harmonic voltage at Bus X

负荷C对母线X的谐波责任表示为负荷C在母线处产生的谐波电压UCh在母线谐波电压UXh上的投影与母线谐波电压UXh模值的比值，即：

其中，γ为相量UXh与UCh的夹角；分别为相量UCh、UXh的模值。用式（2）即可计算出谐波源C在母线X处产生的谐波责任。

由式（2）可看出，ICh与UXh均为可测得量，因此要划分谐波源的谐波责任，首先需要求得背景谐波阻抗Zh。下面首先介绍背景谐波阻抗的计算方法。

2 背景谐波波动情况下谐波责任划分原理

2.1 背景谐波阻抗估计

谐波责任划分的前提是估计背景谐波阻抗，而传统的求解方法都是建立在背景谐波不变的假设上，不适用于背景谐波波动的实际情况。因此，首先探讨背景谐波波动情况下的背景谐波阻抗估计方法。文献［5］提出了基于主导波动量法的谐波阻抗辨识方法，该方法通过统计筛选原理选择出用户主导波动样本，以此估计背景谐波阻抗和用户谐波责任，被后续很多文献应用。因此，考虑到背景谐波波动的特殊情况，本文采用主导波动量法估计背景谐波阻抗。

图3所示为系统侧和用户侧的诺顿等效电路，图中，Ish和ICh分别为系统侧和用户侧h次等效谐波电流；Zsh和ZCh分别为系统侧和用户侧h次等效谐波阻抗。母线X处谐波波动量是用户侧波动和系统侧波动共同作用的结果。根据文献［5］，用户主导的波动量需要满足：

其中，为母线X处谐波电流第k次波动量样本点模值；μ1和σ1分别为母线X的谐波电流波动量模值的平均值和标准差；α为奈尔系数。

图3 系统侧和用户侧诺顿等效电路Fig.3 Norton equivalent circuit of system and customer sides

用式（3）对母线X处的谐波电流波动量样本进行筛选，选择出满足条件的波动量样本点ΔI′Xh，提取出对应的谐波电压波动量样本点ΔU′Xh，用筛选出的ΔI′Xh和 ΔU′Xh进行系统侧谐波阻抗的估计：

2.2 基于分位数回归的谐波责任划分

2.2.1 分位数回归原理

分位数回归法［17］是在最小二乘回归法的基础上提出的一种回归法，由于最小二乘回归法需要满足的要求较高，而且需要迁就异常点，导致回归法缺乏稳健性，由此提出了分位数回归法。分位数回归法稳健性强、使用条件低、信息利用率高，近年来在经济学、医学、环境科学等方面均得到了应用，但是该方法还没有被用于谐波责任划分中。鉴于分位数回归法的优点，本文将其用于求解谐波责任。

值得一提的是，回归法都是利用方程y=sx+b估计斜率s或者是截距b，而现有的大部分谐波责任估计方法都是以准确估计斜率s为目标，这种情况下就要求输入样本点的波动小，斜率的估计精度才会高。而本文采用的分位数回归法旨在准确估计截距b，此时要求输入样本点的波动大，恰好适应本文背景谐波波动的工况，因此能够准确地估计背景谐波波动情况下的谐波责任划分。下面简单介绍分位数回归法的原理。

对于任意实值随机变量Y，它的所有性质都可以由 Y 的分布函数，即 F（y）=P（Y≤y）来刻画。 对于任意的0＜τ＜1，定义随机变量Y的第τ分位数函数F-1（τ）为：

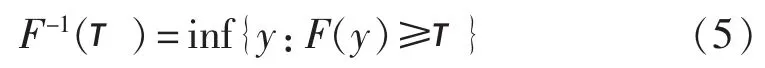
对于 Y 的一组随机样本｛y1，y2，…，yn｝，在第τ分位数的基础上进行回归，使得加权的残差和最小：

其中，ρτ为检验函数；xi为自变量的第i个数据点；为估计的回归系数。

对于任意的 0＜τ＜1，ρτ（u）为：

其中，I（u＜0）为示性函数。由式（7）可以看出，ρτ（u）是分段函数，且 ρτ（u）≥0。

为了积分方便，检验函数ρτ（u）可以改写成：

其中，l（u≥0）和 l（u＜0）为示性函数。

一般最小二乘回归法是通过求解残差平方和得到参数估计值，而分位数回归法则是通过式（6）求解加权残差和得到回归系数的估计值。相比之下，分位数回归具有更强的稳健性，受异常值的影响更小。

2.2.2 分位数回归求谐波责任

在正确估计背景谐波阻抗的前提下，根据求得的背景谐波阻抗划分负荷的谐波责任。现有的方法都是根据谐波责任的定义式（2）求得。若采样数据点数为N，计算过程中相角γ的影响通常是被忽略的，则计算的谐波责任为：

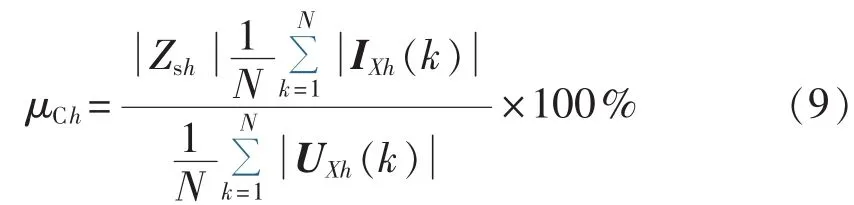
其中，IXh（k）和 UXh（k）分别为第 k 次测量样本点的母线电流和母线电压。

上式中，谐波责任是用母线电流和母线电压的平均值求得。但在背景谐波波动情况下，二者波动都较大，利用该方法计算谐波责任可能会使计算结果偏差较大，且无法反映出谐波电压和谐波电流的变化特征，无法消除背景谐波波动带来的影响。因此，本文采用分位数回归法求取用户的谐波责任。

分位数回归法是利用系统侧谐波电流的波动来划分用户的谐波责任［18］。由图3可得：

推动科技成果转化是促进科技与经济结合、实现创新驱动发展的重要手段，是贯彻落实习近平总书记科技创新思想、实施创新驱动发展战略的一项重大举措。江苏省历来高度重视科技成果转移转化工作，与中科院、北京大学、清华大学等大院大所均建立了长期合作关系，科技成果转移转化活跃、成效显著。

其中，UXh为可测得的量；Ish可以根据已知量求得；Ish、UCh是统计独立的，即 Ish与［Zsh/（ZCh＋Zsh）］UCh是统计独立的，此时可以用Ish和UXh进行分位数回归。其中，系统侧谐波电流Ish由式（11）求得。

式（10）是相量方程，引入相角将其转化成标量。为了便于表达，令 M=ZChZsh/（ZCh＋ Zsh）、N=Zsh÷（ZCh＋ Zsh），M、N 均为相量，则 UXh=MIsh+NUCh。 引入相角后，式（10）变为：

其中，θh为相量 UXh与相量 MIsh之间的夹角；φh为相量UXh与相量NUCh之间的夹角。

取系统侧谐波电流的模值作为自变量、母线谐波电压的模值作为因变量进行分位数回归。回归系数作为的估计值，回归方程在y轴上的截距作为的估计值。根据谐波责任定义式（2），得出用户的谐波责任为：

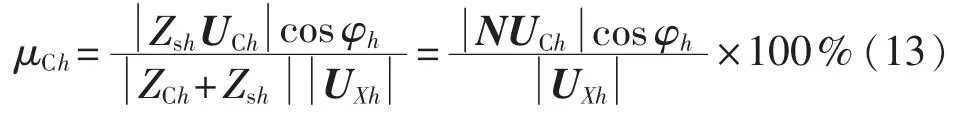
其中，是分位数回归方程在y轴上的截距；是可测得的母线谐波电压模值。因此用式（13）即可求出用户的谐波责任值。

由此可以绘制出用主导波动量法和分位数回归法结合进行谐波责任划分的流程图，如图4所示。

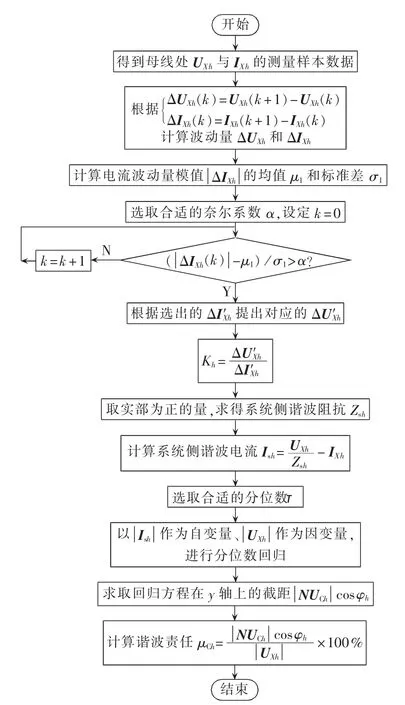
图4 谐波责任划分流程图Fig.4 Flowchart of harmonic responsibility determination

3 IEEE 13节点系统算例仿真

3.1 背景谐波阻抗估计仿真

在IEEE 13节点系统中对典型的谐波阻抗估计方法进行仿真分析，系统模型如图5所示。该系统中有2台发电机、12条支路（包含7台变压器和5条短线路）、7个PQ节点。系统各元件和负荷的参数参照文献［19］。设置负荷8为主要谐波源负荷，母线3作为关注母线，负荷10和负荷11作为另外的非线性负载在母线3处产生背景谐波电压。用MATLAB编写仿真程序，对母线3处负荷8贡献的谐波责任进行评估。

图5 IEEE 13节点系统Fig.5 IEEE 13-bus system

为了减小估计的偶然误差，重复计算100次，取平均值作为估计结果。以5次谐波为例进行仿真，结果如表1所示，其中比较了传统线性回归法［20］、稳健回归法［16］、传统波动量法［21］和主导波动量法的结果，背景谐波阻抗均为标幺值。

表1 负荷8背景谐波阻抗估计结果Table 1 Estimated background harmonic impedances of Load 8

分析表1可知，传统波动量法的估计误差很大，说明该方法在背景谐波波动情况下不能有效地评估负荷的背景谐波阻抗和谐波责任；主导波动量法的估计误差远小于另外3种方法的估计误差，说明在背景谐波波动情况下主导波动量法能精确地估计负荷的背景谐波阻抗。

100次仿真的谐波阻抗误差波动情况如图6所示，因传统波动量法误差较大，故不再绘制。从图6的结果可以看出，主导波动量法求解背景谐波阻抗的误差最小，而且相对于其他的方法，多次计算的误差波动最小，即计算结果稳定性较好。因此可以验证主导波动量法在背景谐波波动情况下计算背景谐波阻抗的可行性和准确性。

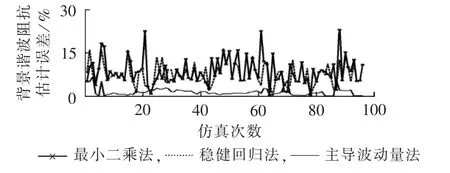
图6 负荷8背景谐波阻抗估计误差统计图Fig.6 Statistical diagram of estimation error for background harmonic impedance of Load 8

3.2 谐波责任划分仿真

在准确估计背景谐波阻抗的条件下，才可进行负荷的谐波责任划分。根据3.1节的结果可知，主导波动量法估计背景谐波阻抗最准确。因此，在用主导波动量法准确估计背景谐波阻抗的前提下，分别用主导波动量、主导波动量与稳健回归相结合（主导波动量+稳健回归）、主导波动量与分位数回归相结合（主导波动量+分位数回归）的方法计算谐波责任，取100次计算的谐波责任和误差平均值，结果如表2所示，100次仿真的误差结果如图7所示。

表2 负荷8谐波责任划分结果Table 2 Results of harmonic responsibility determination of Load 8

图7 负荷8谐波责任划分误差结果统计图Fig.7 Statistical diagram of determination error for harmonic responsibility of Load 8

结合表2和图7的结果可以看出，在用主导波动量法准确估计背景谐波阻抗的前提下，本文采用的主导波动量法与分位数回归法结合的方法估计误差最小，而且误差的波动最小，说明该方法具有较强的准确性和稳健性。

3.3 不同的分位数τ对计算结果的影响

在用分位数回归法计算谐波责任的过程中，需要对分位数进行选取，而且不同的分位数对责任划分的结果影响较大，因此讨论不同的分位数τ对谐波责任计算结果的影响。将τ（0＜τ＜1）取值从0.1增加到0.9，步长为0.1，仿真分析τ 值变化时谐波责任划分的结果如图8所示。

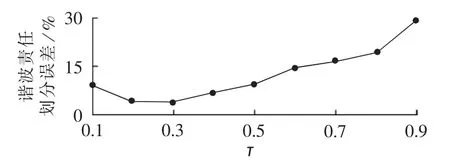
图8 不同τ下的谐波责任划分误差Fig.8 Comparison of harmonic responsibility determination error among different values ofτ

由图8的结果可以看出，当τ从0.1增加到0.9时，谐波责任计算误差呈现先减小再增大的趋势，取值为0.2～0.3时谐波责任计算误差最小。

4 结论

在背景谐波波动情况下，本文采用主导波动量法和分位数回归法结合的方法划分用户的谐波责任。通过算例测试得到如下结论：在背景谐波波动情况下，采用主导波动量法计算背景谐波阻抗精确度和稳定性均高于传统方法；在准确估计背景谐波阻抗的基础上，用分位数回归法划分用户谐波责任能获得优于传统方法的精确度。2种方法结合充分利用了背景谐波的波动，消除了背景谐波波动带来的计算偏差，而且稳健性更好，适用于背景谐波波动工况下的谐波责任划分。

［1］王小君，巩超，和敬涵，等．城轨车辆牵引过程对配电网电能质量的影响分析［J］．电力自动化设备，2015，35（3）：81-87．WANG Xiaojun，GONG Chao，HE Jinghan，etal．Analysison impact of urban rail vehicle traction on distribution network power quality［J］.Electric Power Automation Equipment，2015，35（3）：81-87．

［2］钟斌斌，李妍，张永芳，等．基于H参数的换流器谐波全耦合模型［J］．电力自动化设备，2016，36（2）：45-50．ZHONG Binbin，LI Yan，ZHANG Yongfang，et al．Fully-coupled harmonic model of converter based on H parameters［J］．Electric Power Automation Equipment，2016，36（2）：45-50．

［3］赵勇，沈红，李建华，等.谐波源的识别及其与非谐波源的分离方法［J］.中国电机工程学报，2002，22（5）：85-88.ZHAO Yong，SHEN Hong，LI Jianhua，et al.Approach of identification and separation of harmonic sources［J］.Proceedings of the CSEE，2002，22（5）：85-88.

［4］尹志明.多谐波源系统中谐波责任的量化研究［D］.济南：山东大学，2013.YIN Zhiming．Research of quantifying the harmonic impacts of multiple harmonic sources in power system［D］．Ji’nan：Shandong University，2013．

［5］龚华麟，肖先勇，刘亚梅，等.基于主导波动量筛选原理的用户谐波发射水平估计方法［J］.中国电机工程学报，2010，30（4）：22-27.GONG Hualin，XIAO Xianyong，LIU Yamei，et al.A method for assessing customer harmonic emission level based on the dominant fluctuation filtering principle［J］.Proceedings of the CSEE，2010，30（4）：22-27.

［6］惠锦，杨洪耕，叶茂清.基于阻抗归一化趋势判别的谐波发射水平估计［J］.中国电机工程学报，2011，31（10）：73-80.HUIJin，YANG Honggeng，YE Maoqing.Assessingharmonic emission level based on the impedance gathering trend discrimination［J］.Proceedings of the CSEE，2011，31（10）：73-80.

［7］张巍，杨洪耕.基于二元线性回归的谐波发射水平估计方法［J］.中国电机工程学报，2004，24（6）：50-53.ZHANG Wei，YANG Honggeng.A method for assessing harmonic emission level based on binary linear regression［J］.Proceedings of the CSEE，2004，24（6）：50-53.

［8］贾秀芳，华回春，曹东升，等.基于复线性最小二乘法的谐波责任定量划分［J］.中国电机工程学报，2013，33（4）：149-155.JIA Xiufang，HUA Huichun，CAO Dongsheng，et al.Determining harmonic contributions based on complex least squares method ［J］.Proceedings of the CSEE，2013，33（4）：149-155.

［9］黄舜，徐永海.基于偏最小二乘回归的系统谐波阻抗与谐波发射水平的评估方法［J］.中国电机工程学报，2007，27（1）：93-97.HUANG Shun，XU Yonghai.Assessing harmonic impedance and the harmonic emission level based on partial least-squares regression method［J］.Proceedings of the CSEE，2007，27（1）：93-97.

［10］HUI Jin，YANG Honggeng，LIN Shunfu，et al.Assessing utility harmonic impedance based on the covariance characteristic of random vectors［J］.IEEE Transactions on Power Delivery，2010，25（3）：1778-1786.

［11］华回春，贾秀芳，安海清.背景谐波波动情况下的谐波责任定量计算［J］.电测与仪表，2014，51（7）：1-8.HUA Huichun，JIA Xiufang，AN Haiqing.Harmonic contributions determination under the background harmonic fluctuations ［J］.Electrical Measurement&Instrumentation，2014，51（7）：1-8.

［12］惠锦，杨洪耕，林顺富，等.基于独立随机矢量协方差特性的谐波发射水平评估方法［J］.电力系统自动化，2009，33（7）：27-31.HUI Jin，YANG Honggeng，LIN Shunfu，et al.Assessment method of harmonic emission level based on covariance characteristic of random vectors［J］.Automation of Electric Power Systems，2009，33（7）：27-31.

［13］陈宗碧，肖先勇.基于相关性筛选原理的公共连接点谐波畸变量的分层量化［J］.电测与仪表，2015，52（3）：6-10.CHEN Zongbi，XIAO Xianyong.A method to hierarchical quantification on harmonic distortion of the point of common coupling based on the correlation filtering principle［J］.Electrical Measurement＆ Instrumentation，2015，52（3）：6-10.

［14］孙媛媛，李佳奇，尹志明.基于实测数据的集中式多谐波源责任评估［J］.中国电机工程学报，2014，34（13）：2164-2171.SUN Yuanyuan，LI Jiaqi，YIN Zhiming.Quantifying harmonic impacts for concentrated multiple harmonic sources using actual data［J］.Proceedings of the CSEE，2014，34（13）：2164-2171.

［15］乔黎伟.基于二元线性回归的谐波源责任划分方法研究［J］.工矿自动化，2013，39（7）：73-75.QIAO Liwei.Research ofresponsibilitydivision method of harmonic sources based on binary linear regression ［J］.Industry and Mine Automation，2013，39（7）：73-75.

［16］车权，杨洪耕.基于稳健回归的谐波发射水平估计方法［J］.中国电机工程学报，2004，24（4）：43-46.CHE Quan，YANG Honggeng.Assessing the harmonic emission level based on robust regression method［J］.Proceedings of the CSEE，2004，24（4）：43-46.

［17］奈曼，郝令昕.分位数回归模型［M］.上海：上海人民出版社，2012.

［18］SHOJAIE M，MOKHTARI H.A method for determination of harmonics responsibilities at the point of common coupling using data correlation analysis［J］.IET Generation，Transmission &Distribution，2014，8（1）：142-150.

［19］ABUHASHIM R，BURCH R，CHANG G，et al.Test systems for harmonics modeling and simulation［J］.IEEE Transactions on Power Delivery，1999，14（2）：579-587.

［20］MAZIN H E，XU Wilsun，HUANG Biao.Determining the harmonic impacts of multiple harmonic-producing loads［J］.IEEE Transactions on Power Delivery，2011，26（2）：1187-1195.

［21］王诗超，沈沉，李洋，等.基于波动量法的系统侧谐波阻抗幅值估计精度评价方法［J］.电网技术，2012，36（5）：145-149.WANG Shichao，SHEN Chen，LIYang，etal.A fluctuation quantity based method to evaluate estimation precision of harmonic impedance amplitude at system side［J］.Power System Technology，2012，36（5）：145-149.