线性跟踪误差的指数化投资组合鲁棒优化模型*

安晓敏（西安工业大学理学院，西安710021）



线性跟踪误差的指数化投资组合鲁棒优化模型*

安晓敏
（西安工业大学理学院，西安710021）

摘 要：为消除指数化投资组合中参数的扰动对线性跟踪误差最优解产生的影响，文中针对线性跟踪误差模型，采用鲁棒优化给出了模型参数为矩形不确定集、椭球不确定集的鲁棒模型，分析了该模型由于参数不确定性所造成的缺陷．实证研究表明：采用线性跟踪误差指数化投资组合的鲁棒优化模型的解同时具有鲁棒性与最优性，鲁棒模型与基准模型的收益一致性较好，鲁棒模型的跟踪误差略大于基准模型．

关键词：投资组合；指数化投资；线性跟踪误差；鲁棒优化

基金资助：陕西省教育厅专项科研计划项目（14JK1353）；西安工业大学校长基金（XAGDXJJ1134）

主动型投资，也称积极投资，是通过积极选股、择时以获取超额市场收益的一种投资模式．与之相对应的指数化投资，也称被动投资，是通过被动式管理来达到最小化交易成本，获取平均市场收益的一种投资模式，通常以复制、追踪某一市场指数作为目标．文献［1-2］研究发现，主动型基金可能产生较高的管理和交易费用，从而导致较高的管理成本，因此指数化基金的绩效通常高于主动型基金．传统的指数化基金力求收益率拟合目标指数所代表的市场平均收益率，由此定义投资组合收益与基准指数收益之间的差异为跟踪误差，最小化跟踪误差是传统指数基金的重要目标．

早期指数基金的研究主要是在均值-方差模型的基础上进行的［3-4］，决策目标是二次跟踪误差，即跟踪组合与目标指数收益率之间的方差．近年来，不少学者从线性跟踪误差的角度对该问题进行了研究．文献［5］定义跟踪误差为跟踪组合与目标指数收益率之间的绝对偏差，提出期望-绝对偏差跟踪模型．文献［6］考虑线性跟踪误差模型的三种变形．分别定义跟踪组合与目标指数收益率间的最大偏差、最大下半偏差以及下半偏差为跟踪误差．与二次跟踪误差相比，线性方法能更充分、更直观地反映投资者的投资目的．增强型指数化不同于传统指数基金，是一种积极指数化投资方式，跟踪目标指数的同时，试图获取超过目标指数的收益．考虑给定期望超额收益，跟踪误差最小，或其对偶问题，即给定跟踪误差，超额收益最大，文献［7］提出跟踪误差波动率（Tracking-Error Volatility，TEV）优化问题，并在其具体模型中采用了二次跟踪误差．上述指数化投资组合模型中的参数很难得到精确的估计值．而问题的最优解又会由于这些参数的微小变化产生很大的影响［8］．鲁棒优化可以有效消除参数的扰动对优化模型最优解产生的影响，近年来引起人们的极大关注．文献［9-11］在均值-方差模型基础下，提出了其对应的鲁棒投资组合优化方法．文献［12-13］分别考虑了基于在险价值（Value at Risk，VaR）和条件在险价值（Conditional Value at Risk，CVaR）的鲁棒投资组合优化模型．文献［14］假设参数属于一个凸多面体，考虑采用二次跟踪误差模型，给出了其鲁棒模型为一个线性矩阵不等式约束条件下的优化问题．文中分别研究模型中随机参数为矩形不确定集、椭球不确定集的线性跟踪误差模型，给出其鲁棒优化模型，得到具有鲁棒性的解，并进行实证分析．

1　线性跟踪误差指数化模型

某只指数基金的投资组合中包括n种资产，x∈Rn为组合中各资产的权重．T维列向量B代表目标指数的T个观测收益，T×n维矩阵A为n种资产的收益矩阵，R为事先给定的超额收益率．文献［7］提出的TEV优化问题为给定期望超额收益R，使跟踪误差最小．可表示为二次优化问题

式中：n维列向量；r为n种资产的期望收益率；X为关于决策变量x的可行域，通常为一些线性约束．假设X为

为了给出线性跟踪指数化优化模型，给出四种极小化线性跟踪误差模型．

1．1 四种极小化线性跟踪误差

平均绝对偏差最小化模型（Mean Absolute Deviation，MAD）［6］．求权重矢量x*∈Rn，使得组合与目标指数收益差的绝对值之和的均值最小化，即

式中：Aij，xi，Bt分别为A，x，B中对应角标位置的元素．

最小最大模型求权重矢量x*∈Rn使得组合与目标指数收益之间的最大绝对值偏差最小化，即

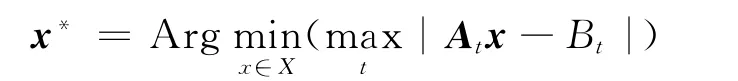
式中：At为矩阵A的第t行．

指数基金的投资目的是尽可能地增大收益，则只有在组合收益低于目标指数收益时，才认为存在风险．此时，宜采取下方风险进行度量，即，最小化组合与目标指数收益间的下半偏差．

同样考虑下半偏差，采用最小最大模型基本思想，则有

1．2线性跟踪误差指数化投资组合模型

1．2．1 平均绝对偏差最小化模型

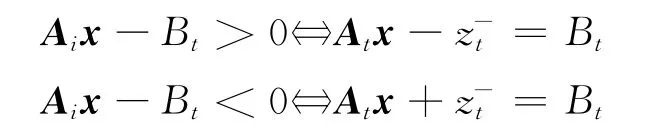
目标函数

对应的指数化模型为

1．2．2 最小最大模型

设z≥0是绝对偏差的上界，有

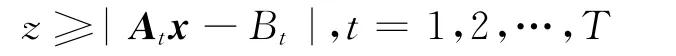
对∀t，可得

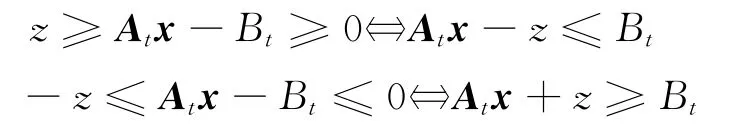
规划模型为

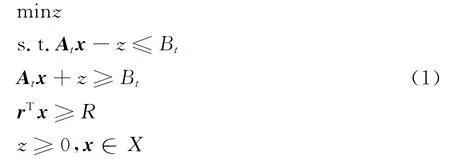
1．2．3 平均绝对下方偏差最小化模型

只要使Atx≤Bt时的偏差的均值最小化．线性规划为

1．2．4 最小最大下方偏差模型

求权重x，满足条件Atx≤Bt下使得偏差最小化，模型为

2　线性跟踪误差的指数化鲁棒优化模型

以平均绝对偏差为例构建指数化鲁棒优化模型．若已知期望收益r，此时相应的模型为确定型优化问题.参数r受随机因素影响，很难对其进行精确估计.相应的模型即为随机最优化问题为

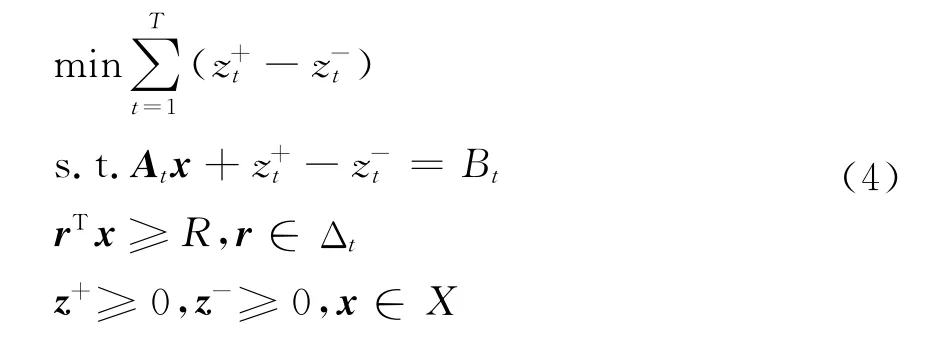
式（4）中随机变量r的取值范围为Δt．研究表明原问题的最优解会因该参数的微小变化产生很大影响［8］，因此采用鲁棒优化理论将原问题转化为易于求解的确定型优化问题，也就是说将参数的不确定性处理成简单形式（如矩形、椭球），较好的拟合参数不确定性，同时将原问题转化为易于求解的确定型优化问题．文献［14］假设参数属于一个凸多面体，考虑采用二次跟踪误差模型，给出了其鲁棒模型为一个线性矩阵不等式约束下的优化问题．目前还未见将鲁棒思想应用至线性跟踪误差的研究．文中分别考虑模型参数为矩形不确定集、椭球不确定集的跟踪误差模型，得到具有鲁棒性的解．

2．1 矩形不确定集的鲁棒模型

假设r的每一个分量属于一个给定的区间，考虑收益率的期望值r属于矩形不确定集

式中：r0，¯r分别为r的期望值向量和波动值向量.

当r属于式（5）所定义的不确定区间时，考虑x为任意给定的投资策略，有

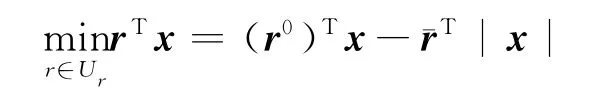
参数属于矩形不确定集下的模型为

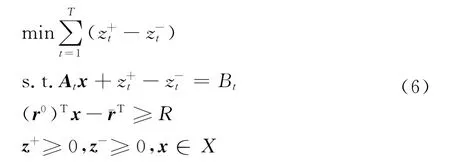
2．2 椭球不确定集的鲁棒模型

对于线性规划，文献［15］给出了当其参数属于椭球型不确定集时的鲁棒问题．

定理1 考虑只含有一个约束条件的线性规划

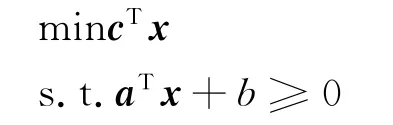
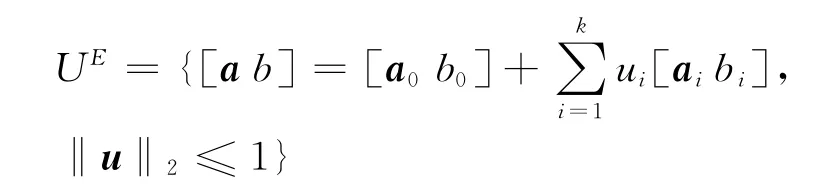
那么，线性跟踪误差所对应的鲁棒问题转化为二阶锥规划

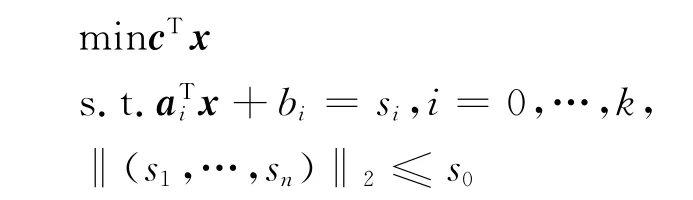
考虑参数r属于椭球不确定集

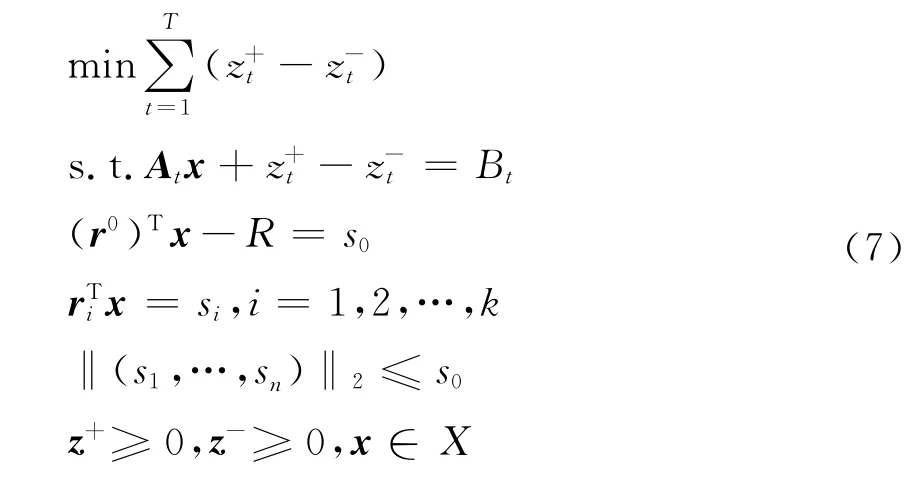
3　实证分析

以香港恒生指数作为基准指数，从其十只成分股长江实业、汇丰、新鸿基、香港铁路、中电控股、香港交易及结算所、中国建设银行、中国海洋石油、中国人寿和中国移动中选取投资组合．取为期24个月的日收盘价，用前22个月的数据构造关于收益率的不确定集，并采用这些数据对文中提出的模型做出优化决策，利用剩余两个月的数据对所得决策进行检测，观察其跟踪误差及收益情况．

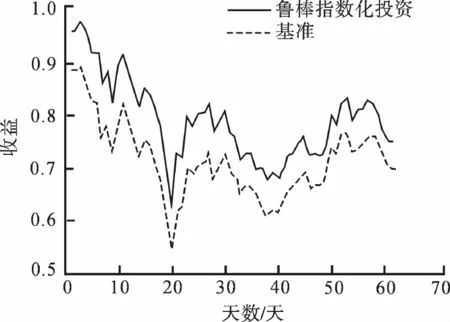
图1　基准和鲁棒（椭球不确定集）指数化投资组合的收益Fig．1 The return of the benchmark and the robust （ellipsoidal uncertainty sets）indexing investment

采用自举技术得到收益率的期望和协方差矩阵的3 000个估计值，然后利用这些估计值对模型中的随机参数构造不确定集．以椭球不确定集为例，原问题的鲁棒模型为二阶锥规划．调用基于Matlab开发的软件包cvx进行求解．图1～2分别为基于指数化投资组合鲁棒模型和基准模型的收益与跟踪误差，由图1～2可以看出鲁棒模型与基准模型的收益率在测试期大致一致，与此同时鲁棒模型的跟踪误差略大于基准模型．

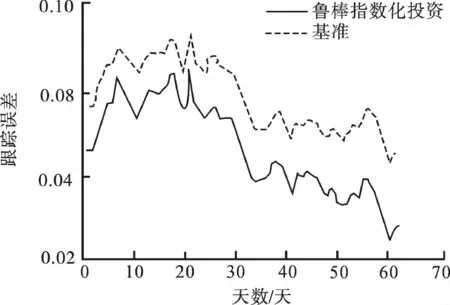
图2　基准和鲁棒（椭球不确定集）指数化投资组合的跟踪误差Fig．2 The tracking error of the benchmark and the robust （ellipsoidal uncertainty sets）indexing investment

4　结论

1）对于指数化投资组合，参数的扰动对线性跟踪误差的最优解产生较大影响．通过采用鲁棒理论研究线性跟踪误差，给出了模型中随机参数属于矩形、椭球不确定集时的鲁棒线性跟踪误差模型，并得到具有鲁棒性的解．

2）模型实证分析结果表明鲁棒模型与基准模型的收益大致一致，而鲁棒模型的跟踪误差略大于基准模型．鲁棒线性跟踪误差模型对现实中的投资决策具有一定的指导意义．

参考文献：

［1］ PAYNE T H，PRATHER L，BERTIN W．Value Creation and Determinants of Equity Eund Performance ［J］．Journal of Business Research，1999，45（1）：69．

［2］ TAYLOR J．A Note on Closet-Indexing［J］．Journal of Economics and Business，2004，56（6）：431．

［3］ MARKOWITZ H M．Portfolio Selection［J］．Journal of Einance，1952，7：77．

［4］ MARKOWITZ H M．Portfolio Selection：Efficient Diversification of Investment［M］．New York：John Wiley＆Sons，1959．

［5］ KONNO H，YAMAZAKI H．Mean-Absolute Deviation Portfolio Optimization Model and Its Application to Tokyo Stock Market［J］．Management Science，1991，37：519．

［6］ RUEOLE M，WOLTER H J，AIMMERMANN H．A Linear Model for Tracking Error Minimization［J］．Journal of Banking and Einance，1999，23：85．

［7］ ROLL R．A Mean-Variance Analysis of Tracking Error［J］．The Journal of Portfolio Management，1992，18：13．

［8］ BLACK E，LITTERMAN R．Global Portfolio Optimization［J］．Einancial Analysts Journal，1992，48：28．

［9］ LOBO M S，BOYD S．The Worst-Case Risk of a Portfolio，Technical Report［EB／OL］．（2001-09-021）［2013-03-05］．http：／／www．stanford．edu／～boyd／papers／pdf／risk＿bnd．pdf．

［10］ TUTUNCU R H，KOENIG M．Robust Asset Allocation［J］．Annals of Operations Research，2004，132：157．

［11］ GOLDEARB D，IYENEAR G．Robust Portfolio Selection Problems［J］．Mathematics of Operations Research，2003，28：1．

［12］ GHAOUI L E，OKS M，OUSTRY E．Worst-Case Value-at-Risk and Robust Portfolio Optimization：A Conic Programming Approach［J］．Operations Research，2003，51（4）：543．

［13］ QUARANTA A G，ZAEEARONI A．Robust Optimization of Conditional Value at Risk and Portfolio Selection［J］．Journal of Banking and Einance，2008，32（10）：2046．

［14］ COSTA O L V，PAIVA A C．Robust Portfolio Selection Using Linear-Matrix Inequality［J］．Journal of Economic Dynamics＆Control，2002，26：889．

［15］ BEN-TAL A，NEMIROVSKI A．Robust Convex Optimization［J］．Mathematics of Operations Research，1998，23 （4）：769．

（责任编辑、校对 张 超）

Robust Indexing Investment Based on Linear Tracking Error

AN Xiaomin
（School of Science，Xi’an Technological University，Xi’an 710021，China）

Abstract：In the indexing investment protfolio，the disturbance of parameters has a great influence on the optimal solution to the original problem．Robust optimization is an effective method to deal with the optimization problem involving uncertainty．Based on the linear tracking error model，the robust model was established with the box and ellipsoidal uncertainty sets as the parameters．Its flaw which results from the uncertainty of parameters was analyzed．The numerical results show that the solution obtained by the new model is both robust and optimal．The return of the robust model is generally consistent with that of the benchmark，while its tracking error is slightly greater than that of the benchmark．

Key words：portfolio；indexing investment；linear tracking error；robust optimization

作者简介：安晓敏（1982－），女，西安工业大学讲师，主要研究方向为最优化理论与算法．E-mail：axmin2014＠sina．com．

*收稿日期：2015-07-12

DOI：10．16185／j．jxatu．edu．cn．2016．01．001

文献标志码：中图号： O221．5 A

文章编号：1673-9965（2016）01-0001-04