酚醛纤维头道并条工艺优化及其对成纱质量的影响

蔡薇琦, 马崇启, 阚永葭， 杨金莲, 李君丽

(天津工业大学 纺织学院, 天津 300387)

酚醛纤维头道并条工艺优化及其对成纱质量的影响

蔡薇琦, 马崇启, 阚永葭， 杨金莲, 李君丽

(天津工业大学 纺织学院, 天津 300387)

为探讨酚醛纤维头道并条工艺优化方案对酚醛纤维成纱质量的影响，在酚醛纤维顺利梳理的基础上，对纺纱工艺中的并条工艺进行优化。通过选取因素后牵伸倍数、罗拉中心距(前×中×后)、并条速度作为研究对象，每个因子选取3个水平，指标值为Y311型条干不匀率和质量不匀率，采用正交分析法，研究不同指标、不同优化方案对成纱质量的影响。分别根据条干不匀、质量不匀、多因素矩阵优化方案的计算得到最优方案。将所得到的3种方案通过同样的纺纱工艺，并用乌斯特条干仪测试3种方案得到的细纱。结果表明，酚醛纤维头道并条中采用多因素矩阵优化得到的方案为最优。

酚醛纤维； 头道并条工艺； 多因素矩阵优化； 质量不均率

酚醛纤维具有优良的抗烧蚀、高热稳定、密度小等特性[1-2]。与碳纤维(1.76～1.80 g/cm3)、芳纶(1.37～1.44 g/cm3)等阻燃纤维相比，酚醛纤维具有轻质的优点，其密度为1.27g/cm3[3]。高温炭化时逸出极少量的烟雾和毒气，主要产物为CO2和H2O，因此酚醛纤维属于环保的阻燃纤维，可用作飞行员、地勤工作人员、船员的消防服装以及航空工业绝缘材料、医院、旅馆中的家具装饰物[4]。

国外已经成功利用酚醛纤维制成防护服装的外层面料，采用纯纺或者与聚酰胺纤维混纺可制成普通阻燃(耐火)工作服、消防服、赛车服和各种防护工作服[5～6]。在国内，目前的研究重点还仅局限于纤维的研究，较少涉及酚醛纤维的纺纱制备，所以现在的酚醛纱线、织物等产品主要依赖进口[3]。

由于酚醛纤维是一种新型纤维，鲜有人针对性地对酚醛纤维纺纱工艺进行研究，本文所进行的试验是在小样纺纱系统中进行，不具备普遍性，仅可对以后酚醛纤维批量化纺纱提供数据参考。

1 材料与方法

1.1 材料与仪器

酚醛纤维，由山东莱芜润达有限公司提供，其性能指标如表1所示。试验中使用的梳理机为DSCa-01A型数字式小样梳棉机，将纤维开松后称取15 g酚醛纤维进行梳理。梳理时出网速度为4.98 m/min，梳理工序参数见表2所示。试验中使用的并条机为DSDr-01数字式小样并条机，预并的工艺参数见表3所示。

表1 酚醛纤维的性能指标Tab.1 Performance index of phenolic fiber

表2 梳理工艺各部件参数Tab.2 Parameters of carding machine of phenolic fibe

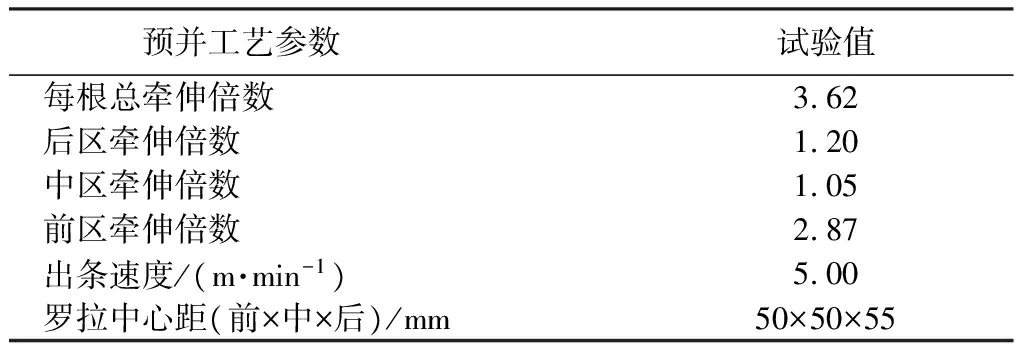
表3 酚醛纤维预并工艺参数Tab.3 Parameters of pre-drawing frame of phenolic fiber

条干不匀率通过Y311型条粗条干均匀度机进行测试，质量不匀率采用条粗质量不匀率测试仪进行。细纱质量通过乌斯特电容式条干均匀度测试仪测试，机器型号为YG191X，成纱线密度为32 tex。

1.2 试验方法

1.2.1 试验流程

优化方案设计→酚醛纤维开松→酚醛纤维梳理→酚醛纤维预并→酚醛纤维头并→生条均匀度测试→选择优化方案→粗纱工艺→细纱工艺→成纱质量对比→确定最佳优化方案。

1.2.2 试验条件

试验是在小样纺纱系统中进行，不具备普遍适应性，仅可对以后酚醛纤维批量化纺纱提供数据参考，该工艺不适合用于其他纤维。本文试验中3种方案采用同样的粗纱工艺与同样的细纱工艺，以达到控制变量的目的。试验采用的机器均为天津市嘉诚机电设备有限公司生产。

酚醛纤维在进行开松、梳理、并条、粗纱、细纱过程中，通过温湿度测试仪测得纺纱室的温度为30～40 ℃，湿度为40%～45%。进行乌斯特条干测试时，温度为(20±2)℃,相对湿度为(65±2)%。

1.2.3 试验设计

并条工序的主要工艺目的：一是用并合的方法改善条子的中长片段不匀；二是用牵伸的方法改善棉条质量，改善纤维的伸直平行度和分离度；三是用重复并合的方法实现纤维最大程度的混合，使棉条达到混合均匀的目的，为成纱质量创造良好的条件[7]。通过多次试验发现：在酚醛纤维并条工艺流程中，牵伸倍数、罗拉中心距、并条速度3个参数是最大影响因素。

生条均匀度与成纱质量密切相关。生条均匀度又称不匀率可分为生条质量不匀率和生条条干不匀率2种，前者表示生条长片段间(5 m)的质量差异情况，后者表示生条每米片段的不匀情况，因此本文试验考察的2个指标分别为条干不匀率和质量不匀率。

选定纤维平均长度Lp为50 mm，预并条的条子定量为15 g/5 m，头道总牵伸倍数6倍。选取因素A为后牵伸倍数，B为罗拉中心距(前×中×后)，C为并条速度，每个因子选取3个水平[8]，试验中所选取的每个水平值均参考了该并条机推荐的范围值，同时参考了以往的纺纱经验。头并工艺试验方案、试验结果见表4。 由于生条条干不匀与生条质量不匀都是越低越好，因此当对条干不匀做直观分析时，分别比较每个因素下各水平试验值的平均值(K值)，并选择最低的一组，即代表该因素最佳的水平试验值，最终获得条干不匀直观分析优化方案A3B1C1。同理可得质量不匀直观分析优化方案为A2B3C1。通过2种优化方案对比可知，不管优化方案选择哪种，因素C均应为C1，而因素A与B却不能确定，因此还需同时考虑2种指标值，即借助正交试验矩阵分析模型。

1.3 矩阵分析模型建立

在正交试验中，由于多指标的存在，需要考虑各因素对各指标的影响程度，以此来解决最优方案的选择问题。而矩阵法可计算出各因素对指标的影响程度，确定权重大小和因素的主次顺序。首先建立一个3层结构模型[9]，如表5所示。表中第1层为指标层，罗列试验中各指标；第2层为因素层，罗列各因素；第3层为水平层，根据各个层次的数据，矩阵的定义如下。

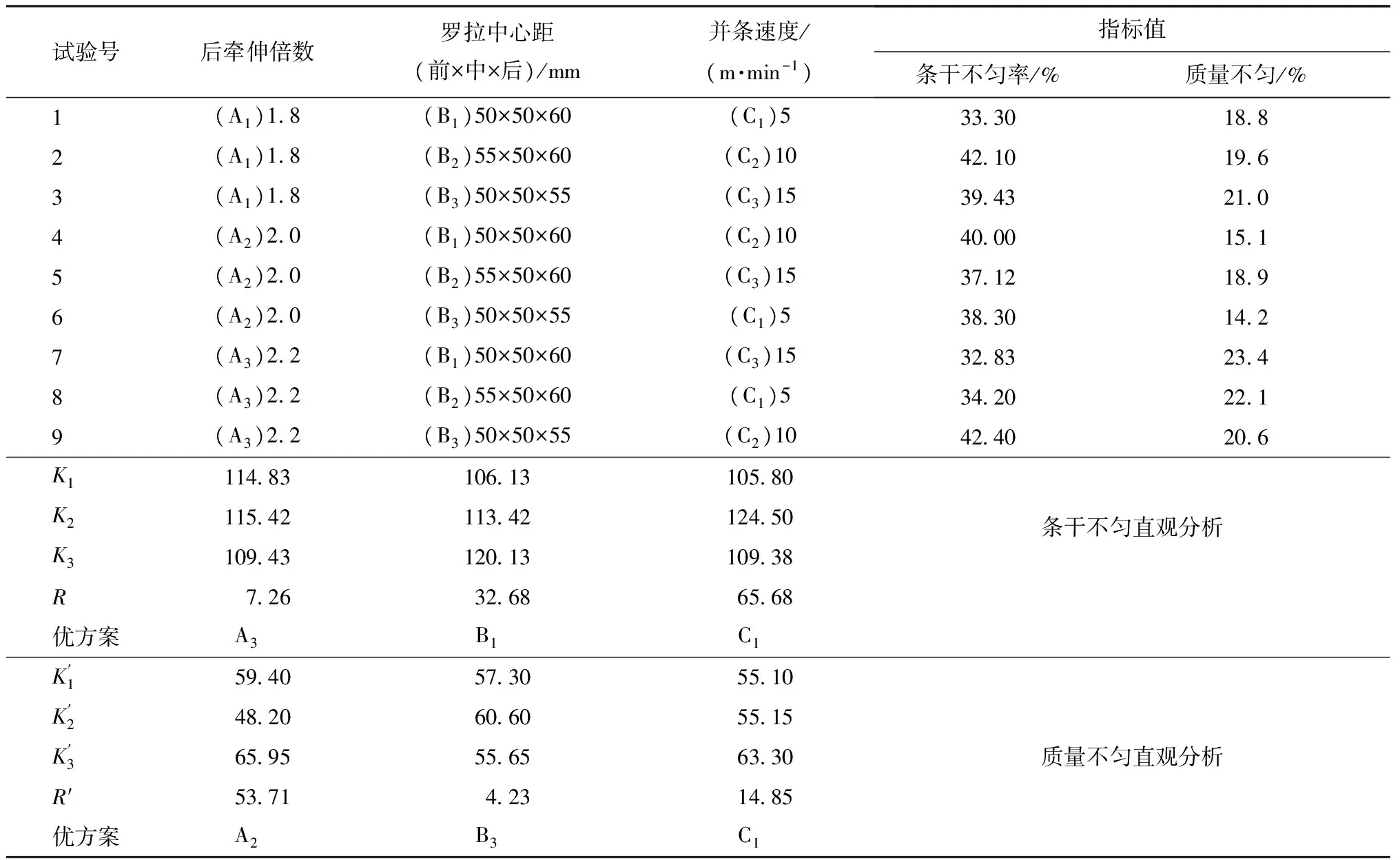
表4 头道并条工艺试验方案及结果Tab.4 Process scheme and result of breaker drawing

定义1：若试验中有n个正交试验因素，每个试验因素有m个水平，则因素Ai第j个水平上的试验指标平均值为kij。当考察指标值表示的含义是越大越好，则令，Kij=kij；当考察的指标值所表示的含义是越小越好，则令Kij=1/kij，建立矩阵式(1)。

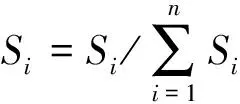
(1)

(2)

(3)

定义4：权重矩阵ω=MTS建立式(4)。

(4)

通过计算即可得到每个因素的权重，以此获得最优方案。

1.4 正交分析计算过程

第1个考察指标为条干不匀，指标值是越小越好，采用矩阵分析法，其权矩阵ω1的计算过程为：

(5)

(6)

(7)

(8)

(9)

第2个考察指标为质量不匀，指标值是越小越好，采用矩阵分析法，其权矩阵ω2的计算过程省略，即得到：

(10)

生条不匀率可分为生条条干不匀率和生条质量不匀率2种。条干不匀又叫短片段不匀，同时质量不匀又叫中、长片段不匀。将表4中9组生条不匀率测试值与质量不匀率测试值进行正交矩阵数据分析发现，生条不匀率与质量不匀率具有线性相关性。故本文视2种指标同等重要，所以总权矩阵为2个指标权矩阵的平均值[10]，计算过程见式(11)。

(11)

根据式(11)的计算结果，将每个因素的3个水平所占的权重分别相加可得：因素A即为后牵伸倍数所占的权重为0.403 2；因素B即为罗拉中心距所占的权重为0.183 7；因素C即为并条速度所占的权重为0.412 9。权重对某一指标而言是指该指标在整体评价中的相对重要程度，因此对于生条的均匀度而言，各因素对生条均匀度的相对重要程度大小为并条速度>后牵伸倍数>罗拉中心距，所以各个因素对试验的指标值影响的主次顺序为：并条速度>后牵伸倍数>罗拉中心距；且通过每个因素的不同水平间的相互比较可知，A2、B1、C1的权重最大，正交试验的最优方案为A2B1C1，即后牵伸倍数为2.0，罗拉中心距(前×中×后)为50 mm×50 mm×60 mm，并条速度为5 m/min。

2 成纱质量对比与分析

为进一步证明通过正交分析矩阵得出的优化方案A2B1C1比单一指标分析得出的优化方案A3B1C1和A2B3C1更好，将3种方案得出的生条进行同样的纺纱工艺，对比细纱质量。即采用控制变量法观察每种方案的细纱质量，结果见表6。表中U为不匀率，CVm为 指标准变异系数，DR为在1.5 m的基准长度内，超过纱条测试平均值5%的细纱长度的总和与基准长度的比值。3种优化方案中，不匀率U和变异系数CVm最低的是A2B1C1方案，同时该方案的细节和粗节都较小，因此从成纱质量的各项指标来看，A2B1C1方案最佳。本文从头道并条的工艺进行分析。

表6 细纱质量Tab.6 Yarn quality

1)牵伸倍数。试验中对于该型号并条机，头并最佳方案是A2B1C1方案，方案中牵伸倍数较好的是2.0。这是因为喂入头并的生条以前弯钩纤维居多，头并后区牵伸以偏大掌握为宜，同时从试验中发现牵伸倍数由1.8增加到2.0时，牵伸效果增加，生条不匀率随之降低。A2B1C1方案比A3B1C1方案中的不匀率降低了11.1%，因此经过本文试验的验证发现头并后区牵伸不能过大，特别是当牵伸倍数为2.2时，生条不匀率改善得不明显，同时会影响成纱的质量。

2)罗拉中心距。对于该型号并条机，在3组罗拉中心距配置中较好的是50 mm×50 mm×60 mm。由于纤维长度及整齐度是决定罗拉握持距的主要因素，纤维长度长、整齐度好可偏大控制，试验中的酚醛纤维是经过整齐切断的化学纤维，因此罗拉隔距都较大。同时经过试验验证发现后区牵伸倍数为2.0时，最佳的罗拉后区中心距应该为60 mm。

3)并条速度。酚醛纤维的并条过程中，并条速度为5 m/min时生条不匀率较好。并条速度提高，会提高生产效率，但条干不匀率会增加，这是因为酚醛纤维属于化学纤维，易产生静电，速度高时易绕罗拉、胶辊，因此并条速度较低会有利于降低条干不匀率。

因此从牵伸倍数、罗拉中心距和并条速度综合考虑A2B1C1方案较优。

3 结 论

酚醛纤维小样试纺先于批量化生产，对批量化生产具有指导作用。在酚醛纤维头道并条优化方案设计、选择与对比及最终方案确定的整个过程中可得到以下结论。

1)根据条干不匀直观分析得到的优方案为后牵伸倍数为2.2，罗拉中心距(前×中×后)为50 mm×50 mm×60 mm，并条速度为5 m/min；根据质量不匀直观分析得到的优方案为后牵伸倍数为2.0，罗拉中心距(前×中×后)为50 mm×50 mm×55 mm，并条速度为5 m/min；根据矩阵模型分析法得到的优方案为后牵伸倍数为2.0，罗拉中心距(前×中×后)为50 mm×50 mm×60 mm，并条速度为5 m/min，且3种优化方案中A2B1C1最佳。

2)综合考虑生条条干不匀率和生条质量不匀率，得到各个因素对正交试验的指标值影响的主次顺序为并条速度>后牵伸倍数>罗拉中心距。

3)从成纱质量各项指标可得出，A2B1C1方案是3种优化方案中最优的方案，说明由矩阵分析法计算得到的优化方案确实具有较好的优化效果，因此在以后的多指标优化方案中可选择矩阵分析法，同时需要综合考虑每个指标所占整体评价的权重，由此得到的优化方案更完善。

4)牵伸倍数、罗拉中心距与并条速度三者对生条不匀率有很大的影响，改变其中每个参数都会影响生条不匀率，因此在做工艺设计时都需要重点考虑这3个因素。

5)本文涉及的工艺设计仅适合用于酚醛纤维并条优化，同时采用的是小样纺纱系统，因此不具有代表性，但该工艺设计思路与优化方案对以后酚醛纤维批量化纺纱可提供数据参考与理论指导。

FZXB

[1] ECONOMY J,LIN Ruey Yuan.Carbonisation and hot stretching of a phenolic fiber[J]. Journal of Materials Science, 1971,6(9):1151-1156.

[2] TOMOMI Okuhashi, YASUAKI Watanable, JUNJI Shimizu Junji, et al. Novel flame-resistant fiber and method of producing the same: US, 3808289, [P]. 974-04-30.

[3] 柳春燕，吕华，吕虎，等.酚醛纤维的研究进展及应用[J].广州化工,2011,39(2):40-42. LIU Chunyan,LÜ Hua,LÜ Hu,et al.Research progress and application of phenolic fiber[J].Guangzhou Chemical Industry,2011,39(2): 40-42.

[4] YING Yonggang,PAN Yanping,REN Rui.Effect of the molecular structure of phenolic novolac precursor resins on the properties of phenolic fiber[J].Materials Chemistry and Physics, 2013,143(1):455-460.

[5] 郭金海,齐鲁.酚醛纤维的研究进展及应用[J].合成纤维工业，2009，32(5):36-39. GUO Jinhai,QI Lu.Research progress and application of phen olic fiber[J],China Synthetic Fiber Industry, 2009,32(5):36-39.

[6] 赫尔.高性能纤维[M].北京: 中国纺织出版社.2004:374. HEARLE JWS.High-Performance Fibers[M].Beijing: China Textile & Apparel Press, 2004:374.

[7] 吕恒正.并条牵伸工业研究[J].棉纺织技术,1996,24(11):16-20. LÜ Hengzheng.The industrial research of process draft in drawing[J].Cotton Textile Technology,1996,24(11):16-20.

[8] 房云玲.并条罗拉隔距对棉条质量的影响[J].山东纺织科技,1998(5):31-32. FANG Yunling. The influence of roller gauge of drawing on the sliver quality[J].Shandong Textile Science & Technology,1998(5):31-32.

[9] 魏效玲,薛冰军,赵强.基于正交试验设计的多指标优化方案研究[J].河北工程大学学报(自然科学版),2010,27(3):95-99. WEI Xiaoling, XUE Bingjun,ZHAO Qiang.Optimization design of the stability for the plunger assembly of oil pumps based on multi-target orthogonal test design[J].Journal of Hebei University of Engineering (Natural Science Edition),2010,27(3):95-99.

[10] 周玉珠.正交试验设计的矩阵分析方法[J].数学的实践与认识,2009,39(2):202-207. ZHOU Yuzhu.Matrix analysis method of the orthogonal experiment design[J]. Mathematics in Practice and Theory,2009,39(2):202-207.

Influence of process optimization of breaker drawing on yarnquality of phenolic fiber

CAI Weiqi， MA Chongqi, KAN Yongjia， YANG Jinlian， LI Junli

(SchoolofTextile,TianjinPolytechnicUniversity,Tianjin300387,China)

To investigate the influence of process optimization of breaker drawing and prioritization scheme on the yarn quality of phenolic fiber, the drawing process was optimized on the basis of the phenolic fiber carded smoothly. By selecting draft multiple factor of the back zone, roller center distance (pro-zone×middle zone×back zone), and the drawing speed as the research objects, with each factor selected by three levels, the index values were unevenness of textile strands and weight unevenness of Y311 type, and by using orthogonal analysis, the influence of different indexes and optimization schemes on yarn quality was studied. Unevenness of textile strands, weight unevenness, and prioritization scheme had been calculated according to multiple factors matrix. The quality of yarns spun by the same spinning process adopting these schemes is tested by USTER tester. The results show that the optimized scheme by using multi factor matrix optimization in the first drawing of phenolic fibers.

phenolic fiber; breaker drawing process; multiple factors matrix optimization; weight unevenness

2015-08-11

2016-06-13

蔡薇琦(1991—)，女，硕士生。主要研究方向为纺纱工艺与织物性能。马崇启，通信作者，E-mail: tjmcq@ tjpu.edu.cn。

10.13475/j.fzxb.20150801806

TS 156

A