电力变压器的有限元建模与绕组松动分析

弓杰伟 ，马宏忠 ，姜 宁 ，王春宁 ，李 勇 ，周 宇

（1.河海大学 能源与电气学院，江苏 南京 211100；2.国网江苏省电力公司南京供电公司，江苏 南京 210019）

0 引言

电力变压器在运输过程中受到碰撞或发生外部短路故障，都可能造成绕组松动和变形故障，变压器在此状态下长期运行将会给电网的安全运行带来很大的危害［1-2］。因此，有必要对电力变压器进行故障诊断研究。文献［3］针对电力变压器发生绕组变形将会导致漏感参数发生变化的基本特征，提出通过改变绕组的基本几何尺寸模拟绕组变形，研究了绕组变形状态和漏感参数变化量之间的关系。文献［4］采用基于分段函数拟合磁化曲线的改进方法，并考虑不饱和励磁的非线性，求解出三维棱边有限元磁场。上述研究的侧重点都在于电与磁方面，而变压器内部故障、性能改变，都直接或间接地在变压器外部振动中有相应表现，所以通过振动来诊断变压器的潜伏故障也是一种有效手段。

振动法能够检测出故障绕组和铁芯的状况，对其进行充分研究有良好的应用前景［5］。文献［6］针对变压器绕组多种故障并发的工况，在分析变压器绕组振动机理的基础上，提出了一种基于集合经验模式分解的振动信号特征提取方法。文献［7］在分析变压器振动在线监测实际功能与数据需求的基础上，应用LabVIEW/Compact RIO软硬件平台设计和研制了电力变压器振动在线监测系统。文献［8］从绕组结构特点及绝缘垫块的力学特性出发，建立了变压器稳定运行时绕组振动的等效系统模型，推导出了绕组振动的位移、速度、加速度的表达式以及计算绕组固有频率的方法。

在复杂结构的动态分析中，需要利用离散化方法建立结构的离散化模型。有限元方法就是将结构离散为有限个单元，随后将各个单元的质量矩阵、刚度矩阵集合成总的质量矩阵、刚度矩阵，从而得到总的系统的有限元模型［9］。文献［10-11］建立了变压器绕组的有限元模型，进行了模态分析，并与实验测得的固有频率进行对比，证明了有限元模型的正确性，但没有研究绕组带电情况下在不同预紧力时的振动响应特性，因而不能根据绕组的外部振动特性预测绕组的压紧程度。文献［12］对不同预紧力下的变压器模型进行了稳态响应计算，并与绕组工作时的测试结果进行对比，得到了计算结果与测试结果在趋势上一致的结论，但其在谐响应分析时使用的完全法不可使用预应力选项，而且完全法采用完整的系统矩阵来进行计算，在计算速度及开销方面有一定的局限性。

本文采用ANSYS Workbench对变压器进行模态分析，得到模型在不施加任何工作载荷时的固有频率及相应振型，并与实验结果进行了对比分析。使用模态叠加法对得到的振动特性数据进行谐响应分析，施加一定的激励力来模拟变压器带电运行的情况，并与短路试验结果进行对比，得出轴向预紧力对绕组机械动力学特性的影响。

1 绕组振动机理与有限元建模

1.1 振动原理

从机械结构的角度来看，电力变压器器身表面的振动与变压器绕组和铁芯的压紧状况密切相关。变压器本体的振动主要来源于磁致伸缩及漏磁引起的铁芯振动和电磁力引起的绕组振动［13］，而漏磁引起的铁芯振动与其他振动相比较为微弱，所以一般可忽略漏磁的影响。由于在副边短路时，外施电压很小，则铁芯中磁通很少，此时由磁致伸缩引起的铁芯振动可以忽略不计，而通过变压器油和箱壁传递到油箱表面的振动信号主要就是由绕组引起的。

由毕奥-萨伐尔定律可得：

其中，dB为电流元产生磁场的磁感应强度；μ0为真空中的磁导率；I为源电流；dl为源电流微小线元素；r为某点与电流元间的距离；r为电流元指向待求场点的单位矢量。

由式（1）求得线圈产生磁场的磁感应强度为：

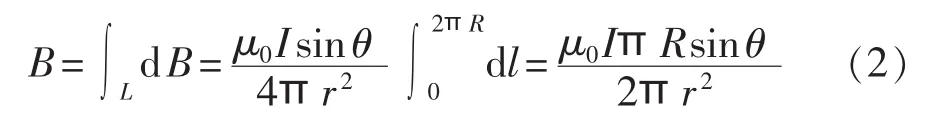
其中，B为B的幅值；L为积分路径；R为线圈半径；θ为某点与电流元的夹角。

由F=IBL可知，在漏磁场作用下绕组产生的电动力与电流的平方成正比，即F=kI2。电力变压器稳定运行时的电流为 I0cos（ωt）（ω为变压器工作角频率），则：

由式（3）可知，电动力可以分为一个直流分量和一个2倍于工频的交流分量。直流分量对线圈的作用相当于施加一个恒定的力，该作用力相对于预紧力可以忽略不计［14］。由此可见，在工频电源下的激励力频率为100 Hz。由于磁化曲线的非线性以及变压器结构复杂等原因会使绕组振动频谱中含有高次谐波［15］，所以电动力引起的绕组振动频率是100 Hz及其谐振频率。

1.2 建模说明

本文通过ANSYS Workbench有限元建模对油浸式变压器进行绕组松动研究。ANSYS软件是进行有限元分析的工具，具有强大的分析功能，但对复杂模型的搭建非常困难。而计算机辅助设计CAD（Computer Aided Design）软件有着强大的三维图形处理功能，并且能够通过导入接口方便快捷地导入ANSYS软件中。故本文先通过常用CAD软件Pro/Engineer来进行模型的搭建。

本文的研究对象是一台电压等级为10 kV的油浸式电力变压器。该变压器的绕组是由绝缘电磁线紧密缠绕并加上一定预紧力构成，故在建模过程中可以将线圈等效为若干实体圆环，其余部分则按照原尺寸进行搭建。通过Pro/Engineer绘制的变压器模型如图1所示。

模型中各零件材料参数的设置对于有限元分析而言是十分关键的部分，而绝缘垫块的非线性特性会导致其弹性模量随着所受预紧力的变化而变化。由于垫块的材料及其松散的结构，当垫块装入变压器中时会吸收变压器油，而施加在垫块上的压力载荷变化时，又会使垫块排出或者继续吸收变压器油，这就使得绝缘垫块的弹性系数与装配后的压紧程度有关。故需要计算出不同预紧力下绝缘垫块的弹性模量，以此来模拟绕组松动对变压器的影响。

图1 通过Pro/Engineer绘制的变压器模型Fig.1 Transformer model drawn by Pro/Engineer

由文献［16］可知，垫块的应力-应变关系在一定范围（0～103MPa）内可表示为：

其中，σ为应力；ε为应变；a=1.05×102MPa为线性常数；b=1.75×103MPa为硬化系数。由式（4）可得垫块的弹性模量为：

绕组松动程度可以根据预紧螺杆上力的大小得到，而预紧力则可通过电阻应变片和桥式电路测得。其原理是预先将应变片贴在螺杆的侧面，螺杆压紧后通过应变片变形引起的电阻变化来较为精确地测量力的大小。根据式（4）、式（5）预紧力的大小和螺杆截面积可以计算出不同预紧力下垫块的应变和弹性模量，如表1所示。由此可在有限元模型中通过设置不同预紧力下垫块的弹性模量来模拟绕组松动对变压器的影响。

表1 不同预紧力下垫块的应变和弹性模量计算值Table 1 Calculated strain and elasticity modulus of supporting block for different pre-compressions

2 模态分析

2.1 计算固有频率

模态分析用于确定结构的振动特性，其实质是求解具有有限个自由度的无阻尼和无外载荷状态下的运动方程，得到的方程特征值和特征向量，即为各个模态的固有频率和模态振型。模态分析是为了确定各阶频率以及振型对结构的不同影响，通过合理设计使变压器固有频率远离激励力频率，避免引起共振，并以此预测变压器绕组结构在其固有频率范围内在外部激励作用下的实际振动响应。由于振动特性决定结构对于各种动力载荷的响应情况，所以任何形式的动力学分析都必须建立在模态分析的基础上。

本文先对变压器模型中各部分零件进行合理剖分来控制计算时间和计算精度。模型以0.04 m的单元大小自由划分网格，网格密集程度由各零件的刚度大小决定，刚度越小，则网格越密集，计算越复杂。本文模型可以划分出164033个节点和24173个单元。模型计算前需对其施加边界条件，由此可以求得特征值和特征向量。完全约束底面钢板的底部位移以及4根螺杆的底部位移，并在螺杆的顶部施加预应力来模拟预紧力的影响。

在实际结构中，往往是低阶固有频率及其振型对动态特性的影响最大。故利用ANSYS有限元计算方法，对变压器进行三阶模态分析。图2为预紧力大小与模型固有振动频率之间的关系曲线。由图可知，绕组的预紧力越小，其固有频率就越低。这是因为电力变压器绕组是一个复杂的多自由度系统，绕组的结构、阻尼和非线性特征对绕组的轴向固有频率都有一定的影响［11］，而绕组的固有频率在很大程度上取决于装配后的压紧程度，即随着预紧力的降低，绕组结构变得松散，绝缘垫块的刚度也随之减小，从而固有频率逐步向下偏移。

图2 预紧力与模型固有频率的关系曲线Fig.2 Curve of inherent frequency of model vs.pre-compression

2.2 激振实验

根据文献［15］可知，顶部油箱结构简单且和铁芯绕组直接相连，并承载着整个铁芯和绕组的重力，导致顶部结构稳定，而且绕组振动传递至铁芯后通过结构连接件传递到油箱顶部，衰减较少，能够较为准确地反映绕组振动信号，所以本实验测点尽量布置在油箱顶部，如图3所示。图中，1、2、3号测点分别位于 C、B、A 相绕组正上方，4、5、6 号测点位于高压绝缘套管一侧的正面，7、8、9号测点则位于低压绝缘套管一侧，10、11号测点分别位于变压器两侧（加括号的测点为图3中视角不可见测点）。

图3 测点布置图Fig.3 Layout of measuring points

图4 不同测点在50%额定预紧力时的频率响应曲线Fig.4 Frequency response of different measuring points with 50%of rated pre-compression

本文采用锤击法［17-18］，即用冲击锤对油箱进行激振，测量敲击的力信号和吸附在测点的加速度传感器测量的振动信号，将获得的时域信号利用傅里叶变换转换成频域信号，并对数据进行传递函数分析，绘制出各测点的频率响应曲线。其中，对同一种预紧力状态下的变压器进行3次敲击，从3次敲击的频率响应曲线中观察测点的各阶固有频率并进行比较，提取各阶固有频率中一致性较好的频率作为该测点的固有频率。由于绕组本身结构较为紧密以及线圈等的重力作用，所以在预紧力很小的情况下绕组结构变化不大，其固有频率的变化也较小。在50%的额定预紧力（变压器出厂时的预紧力，计算值为6268 N）下，各相绕组结构会随预紧力的改变而发生明显变化，而各测点处测得的固有频率则与结构有很大关系，图4即为在1、2、3号测点处所得到的频率响应曲线（Y为单位激振力下所产生的振动响应）。表2为不同预紧力下固有频率前3阶计算值和实验值的比较。其中，计算值为变压器模型整体的固有频率；实验值为在不同测点测得的固有频率，与该测点处的结构有关；p为预紧力与额定预紧力的百分比。从表2中可以看出，在额定预紧力下，变压器的1阶固有频率在115 Hz左右，而当预紧力降低时，变压器的各阶固有频率也大致呈现下降的趋势。

表2 不同预紧力下固有频率的计算值和实验值Table 2 Calculative and experimental inherent frequencies of different pre-compressions

2.3 结果分析

a.由图4可以看出，在50%的额定预紧力下，油箱顶部3个测点的固有频率基本一致，仅在幅值上有差别。除去低频干扰后，变压器前3阶固有频率分别为99 Hz、157 Hz和206 Hz左右。在3个测点中，2号测点固有频率的幅值最大，其次为1号测点，3号测点固有频率的幅值最小。这是由于2号测点位于中间位置，激振后其他部分的振动信号叠加而产生了更强的信号。

b.从图4中可以发现，此状态下的1阶固有频率已经十分接近100 Hz，当施加给变压器100 Hz的激励力时，就会发生共振现象，会使绕组的振动有大幅度的增长，危害变压器的运行安全，所以需增大预紧力使其避免接近100 Hz。

c.表2中的数据表明有限元计算值与实验值较为吻合，有相同的趋势，即随着预紧力的增大，固有频率也在增大。其中，当预紧力较小（低于50%的额定预紧力）时，计算结果的误差较大。这是因为绕组缺少预紧力的约束，线圈之间的振动无法有效传播，而在计算时无法考虑太过复杂的情况，因此误差相对较大。

3 谐响应分析

3.1 频率响应分析

谐响应分析是为了确定结构在已知频率和幅值的正弦载荷作用下的稳态响应，计算结构在不同频率的振动情况，并得到振动幅值曲线。变压器工作时，在电磁力的激励下，线饼的振动可以看作是简谐运动，谐响应分析可以确定绕组的持续动力性能，使其避免强迫振动所引起的共振。

本文使用模态叠加法，其是将模态分析得到的振型与因子相乘，并通过求和来计算出结构的响应。模态叠加法比完全法求解更快且开销更小，包含预应力效果，而且可以使解按结构的固有频率聚集，产生更平滑、更精确的响应曲线图。进行谐响应分析时，先设定计算频率范围为0～400 Hz，分为400个子步，设置阻尼比率为0.02，并在绕组上施加一个1.5×10-4×g（g为重力加速度）的加速度来模拟电磁力的影响，以此计算出变压器的形变、加速度以及应力响应。图5是预紧力为3134 N时不同位置的位移响应曲线，波形由上至下分别为铁芯顶部、C相顶部和C相正面的位移响应曲线，其幅值表示的是相对值，表征各点在某阶固有频率上振动量的相对比值，反映该固有频率上振动的传递情况，并不反映实际振动的数值。从图中可以看出，当激励力频率为100 Hz时，变压器模型有较大的幅值。这是因为模型在100 Hz附近有1阶固有频率，从而发生共振，导致了较大的振动。

图5 预紧力为3134N时不同位置的位移响应曲线Fig.5 Displacement response of different positions with pre-compression of 3134N

通过计算带电情况下变压器在不同预紧力时的振动响应特性，找出故障特征明显的振动信号，并与绕组工作时的测试结果对比，可诊断出变压器内部是否出现故障，而且还可以进一步判断故障位置。在对谐响应分析结果的处理中，以额定预紧力时的响应为参考点，绘制变压器不同位置处100 Hz的响应与预紧力正常时的响应对比的曲线图，如图6所示。

从图6中可以看出，与正常情况相比，铁芯顶部的响应变化程度随着预紧力的减小而不断增大，这是因为绕组松散程度加强，振动增大，而铁芯的刚度较大，所以呈现单调的趋势；其他部分测点则是先增大后减小，这与固有频率的分布、阻尼和非线性特征等都有一定的关系。

3.2 实测试验

变压器短路试验测点布置如图3所示，主要考虑1—6号加速度传感器，分别位于油箱顶部和高压绝缘套管侧正面。因为变压器绕组产生的振动主要与电流平方有关，铁芯产生的振动主要与电压的平方有关，所以为了尽量减小所测得信号中的铁芯振动分量，应该使电压尽可能小而电流尽可能大。故将实验变压器低压侧三相绕组短路后，在高压侧通过调压器调节外加电压，使低压侧短路电流达到额定电流145 A。在测取振动信号时，对每个振动传感器进行3次采样，每次测取的信号长度为10 s，采样频率为10 kHz，进行傅里叶变换的频率分辨率为0.1 Hz。信号采集完成后，对整周期截取的振动信号进行滤波处理，再进行时频变换，得到各振动传感器每次采样的频谱图并进行比较，从而可以排除3次采样中差别较大的振动信号。变压器绕组的预紧力与额定预紧力的百分比分别为0、50%和100%时，1、2号测点的振动信号频谱图分析比较如图7所示。图8为不同预紧力下在1—6号测点处100 Hz的加速度变化曲线图。

图6 不同位置处不同预紧力的相对响应Fig.6 Curve of relative response vs.precompression for different positions

图7 预紧力不同时，1、2号测点的振动频谱分析Fig.7 Spectrum of measuring point No.1 and No.2 for different pre-compressions

图8 不同位置处不同相对预紧力的加速度Fig.8 Curve of acceleration vs.relative precompression for different positions

3.3 结果分析

a.从图7可以看出，绕组振动信号主要是以100 Hz为基频的周期性信号，也包含50 Hz的奇次谐波分量，这是由于变压器结构不对称及铁芯磁滞回线的非线性造成的［19］。图中2号测点的振动信号比1号测点的复杂，不仅有基频分量，还包含了其他频次的高次谐波。50%的额定预紧力下，2个测点的基频加速度比在其他2种状态下要大，这是因为此时2个测点处结构的固有频率都接近100 Hz，产生了共振。

b.对比图6和图8可以发现，预紧力变化时，100 Hz振动量的变化与计算结果的趋势相似。从图8中可以发现，在实测实验中大部分测点都没有呈现单调的趋势，而是会在某个预紧力下达到最大值，这是因为在绕组松动到一定程度后，变压器的固有频率会降到100 Hz附近，引起了共振，导致振动信号增大。而当预紧力继续降低后，固有频率偏离基频，又会使得振动加速度降低。在没有预紧力的情况下，计算结果会有较大的误差，这是由于没有预紧力的约束，线圈与线圈之间的振动无法有效传播和相互影响。

4 结论

本文从机械动力学角度通过有限元建模分析和实验对变压器的绕组松动缺陷进行了研究，根据有限元计算结果和实验结果得到了如下结论。

a.在额定预紧力下，实验变压器的1阶固有频率在115 Hz左右，而当绕组压紧降到一定程度后，其固有频率会降低至100 Hz，这时由于绕组电动力的基频也为100 Hz，所以会引起较大的振动。若长期在振动剧烈的状态下运行，则会导致变压器故障。

b.将带电情况下的变压器振动信号的100 Hz幅值的计算结果与短路试验结果对比，可以发现预紧力对基频幅值有较大的影响，可以作为特征信号来诊断绕组松动缺陷。其中大部分测点有较为相似的趋势，其峰值则与该位置结构的固有频率有关。变压器绕组的松动本质上影响了其本身的动力学性能，因此可以通过计算变压器在不同预紧力时的振动响应特性，并与历史数据比较，从而判断绕组是否发生松动。

由于有限元模型是根据变压器机械结构来建立的，故此方法可以应用于所有结构相同的变压器，具有一定的普遍性。通过建立变压器有限元模型，不仅可以判断绕组是否发生松动，而且可以根据不同测点位置的信号变化对故障进行初步定位，这对研究和诊断变压器故障有一定的意义。

参考文献：

［1］BERLER Z，GOLUBEV A，ROSOV V，et al.Vibro-acoustic method of transformer clamping pressure monitoring［C］//Conference Record of 2000 IEEE International Symposium on Electrical Insulation.Anaheim，CA，USA：IEEE，2000：263-266.

［2］冯永新，邓小文，范立莉，等.大型电力变压器振动法故障诊断与发展趋势［J］.变压器，2009，46（10）：69-73.FENG Yongxin，DENG Xiaowen，FAN Lili，et al.Vibration method for large power transformer fault diagnosis and its trend ［J］.Transformer，2009，46（10）：69-73.

［3］李朋，郝治国，张保会，等.基于有限元法的变压器漏感计算在绕组变形中的应用［J］.电力自动化设备，2007，27（7）：49-53.LI Peng，HAO Zhiguo，ZHANG Baohui，et al.Leakage inductance calculation based on finite element method for power transformer and its application to winding deformation analysis［J］.Electric Power Automation Equipment，2007，27（7）：49-53.

［4］潘超，王梦纯，蔡国伟，等.变压器直流偏磁场路耦合计算中的磁化曲线拟合［J］.电力自动化设备，2014，34（4）：49-52.PAN Chao，WANG Mengchun，CAI Guowei，et al.Magnetization curve fitting in field-circuit coupling computation for DC-biased transformer［J］.Electric Power Automation Equipment，2014，34（4）：49-52.

［5］汲胜昌，李彦明，傅晨钊.负载电流法在基于振动信号分析法监测变压器铁心状况中的应用［J］.中国电机工程学报，2003，23（6）：154-158.JI Shengchang，LI Yanming，FU Chenzhao.Application of on-load current method in monitoring the condition of transformer’s core based on the vibration analysis method ［J］.Proceedings of the CSEE，2003，23（6）：154-158.

［6］李莉，朱永利，宋亚奇.变压器绕组多故障条件下的振动信号特征提取［J］.电力自动化设备，2014，34（8）：140-146.LI Li，ZHU Yongli，SONG Yaqi.Feature extraction for vibration signal of transformer winding with multiple faults［J］.Electric Power Automation Equipment，2014，34（8）：140-146.

［7］周求宽，万军彪，王丰华，等.电力变压器振动在线监测系统的开发与应用［J］.电力自动化设备，2014，34（3）：162-166.ZHOU Qiukuan，WAN Junbiao，WANG Fenghua，et al.Design and implementation of online vibration monitoring system for power transformer［J］.Electric Power Automation Equipment，2014，34（3）：162-166.

［8］汲胜昌，王俊德，李彦明.稳态条件下变压器绕组轴向振动特性研究［J］.电工电能新技术，2006，25（1）：35-38.JI Shengchang，WANG Junde，LI Yanming.Research on axial vibration characteristics of transformer windingsundersteady condition［J］.Advanced Technology of Electrical Engineering and Energy，2006，25（1）：35-38.

［9］谢坡岸.振动分析法在电力变压器绕组状态监测中的应用研究［D］.上海：上海交通大学，2008.XIE Poan.Study on application of vibration analysis to the condition monitoring of power transformers windings［D］.Shanghai：Shanghai Jiao Tong University，2008.

［10］余小辉，李岩，井永腾，等.变压器绕组模型的固有频率计算与分析［J］.变压器，2010，47（7）：6-8.YU Xiaohui，LIYan，JING Yongteng，etal.Calculation and analysis of natural frequency of winding model of transformer［J］.Transformer，2010，47（7）：6-8.

［11］李洪奎，李岩.不同预紧力下变压器绕组轴向振动模态分析［J］.电机与控制学报，2010，14（8）：98-101.LI Hongkui，LI Yan.Axial vibration modal analysis of transformer windings under different levels of pre-compression［J］.Electric Machines and Control，2010，14（8）：98-101.

［12］袁国刚，谢坡岸，静波，等.轴向预紧力对变压器绕组振动特性的影响［J］.噪声与振动控制，2004，1（2）：25-27.YUAN Guogang，XIE Poan，JING Bo，et al.Influence of axial pre-compression on the vibration of transformer windings［J］.Noise and Vibration Control，2004，1（2）：25-27.

［13］WEISER B，PFUTZNER H.Relevance of magnetostriction and forces for the generation of audible noise of transformer cores［J］.IEEE Trans on Magnetics，2000，36（5）：3759-3777.

［14］洪凯星，潘再平，黄海.电力变压器绕组轴向振动的建模与分析［J］.变压器，2010，47（12）：32-36.HONG Kaixing，PAN Zaiping，HUANG Hai.Modeling and analysis of winding axial vibration of power transformer［J］.Transformer，2010，47（12）：32-36.

［15］赵宏飞，马宏忠，陈楷，等.基于振动信号的变压器绕组松动实验研究［J］.中国电力，2014，47（1）：13-16.ZHAO Hongfei，MA Hongzhong，CHEN Kai，et al.Experimental study oftransformerwinding loosenessbased on vibration signals［J］.Electric Power，2014，47（1）：13-16.

［16］PATEL M R.Dynamic response of power transformers under axial short circuit forces partⅡ-windings and clamps as a combined system［J］.IEEE Transactions on Power Apparatus and Systems，1973，92（5）：1567-1576.

［17］马宏忠，赵宏飞，陈楷，等.基于振动的变压器铁芯松动判定方法［J］.电力系统自动化，2013，37（14）：101-106.MA Hongzhong，ZHAO Hongfei，CHEN Kai，etal.Determine method for transformer core looseness based on vibration ［J］.Automation of Electric Power Systems，2013，37（14）：101-106.

［18］赵宏飞，马宏忠，李凯，等.电力变压器油箱固有频率测试及其影响分析［J］.电力自动化设备，2013，33（11）：165-169.ZHAO Hongfei，MA Hongzhong，LI Kai，et al.Test and analysis of inherent frequency of power transformer tank［J］.Electric Power Automation Equipment，2013，33（11）：165-169.

［19］王春宁，朱跃光，马宏忠，等.基于振动信号和小波神经网络的变压器故障诊断［J］.中国电力，2014，47（4）：75-79.WANG Chunning，ZHU Yueguang，MA Hongzhong，et al.Fault diagnosis of power transformer based on vibration and wavelet neural network［J］.Electric Power，2014，47（4）：75-79.