风电功率爬坡事件作用下考虑时序特性的系统风险评估

何成明，王洪涛，王春义，韦仲康

（1.山东大学 电网智能化调度与控制教育部重点实验室，山东 济南 250061；2.国网山东省电力有限公司，山东 济南 250001；3.国网冀北电力有限公司，北京 100053）

0 引言

随着风电渗透率的提高，风电的随机性和波动性对系统的影响越来越受到关注［1］。特别是当发生极端气象事件（如锋面过境、雷暴、大风等）时，有可能引发风电功率爬坡事件［2-3］，即风电出力在短时间内发生单向大幅度变化。尤其是我国风电大规模高集中接入模式下，一旦发生风电功率爬坡事件将会对电力系统的有功平衡造成严重影响，甚至引发系统频率失稳、切负荷等问题［4-5］。因此，研究风电功率爬坡事件作用下的系统运行风险评估模型和方法，实现含风电电力系统安全风险预警是至关重要的。

风电功率爬坡事件对电力系统运行风险影响的评估需要以爬坡预测信息为依据，针对爬坡事件的预测方法国内外已有相关研究［6-8］，受预测水平限制，爬坡预测系统提前6 h只能给出概率性预测结果且精度较低；小时前的爬坡预测结果精度相对较高，但受常规机组有功调节速度及最小启动时间限制，难以采取相应的控制措施来维持爬坡事件发生过程中的有功平衡［4］。

针对风电并网对电力系统有功平衡的影响，文献［9］将风电场可用容量的概率分布与可用风能的概率分布相结合，计算出风电场输出功率的概率分布，并据此评估了风电场接入对系统可靠性的影响。文献［10］在考虑负荷变化、常规机组强迫停运率和风电功率波动的情况下对系统调峰充裕性进行了评估，有效反映了风电接入容量对系统有功调节容量需求的影响，但评估过程中未考虑常规机组有功调节速率对评估结果的影响。文献［11］在综合考虑风电功率波动特性、负荷波动以及常规机组调节容量及速率的基础上对风电随机波动影响下系统执行调度计划过程中的运行风险进行了评估。与常规风电功率随机波动不同，爬坡事件具有较强的时序特性，表现为风电功率 30 min～5 h的持续单向变化［12］，上述研究集中在风功率的统计特性对含风电电力系统的有功调节充裕性的影响，常规风电功率波动在不同时段间无关联，研究中评估时段间相互独立，难以适用于爬坡事件作用下系统运行风险评估过程。爬坡事件作用下系统有功不平衡量是风电功率爬坡和常规机组计划外停运共同作用的结果［4］，两者之间相互独立，且相互之间的时序关系对评估结果有较大影响。传统的风险评估模型中，常规机组停运概率通常取定值，文献［13］考虑了常规机组停运概率的时间相关性，提高了发电计划风险评估的准确性，但评估过程中未对常规机组的停运时刻加以区分，无法考虑其对常规机组有功调节速率的要求。

为便于调度人员针对风电功率爬坡事件采取相应预防控制措施，本文提出了考虑时序特性的风电爬坡事件风险评估模型，分析了爬坡事件对系统运行风险的影响程度，并通过算例对所提模型有效性进行了仿真验证。

1 风电功率爬坡事件风险评估原理

与常规风电出力波动不同，风电功率爬坡事件由极端气象条件引起，一旦发生将持续多个时段，且爬坡过程中时段之间相互关联。选取爬坡事件的开始时间、持续时间和爬坡量作为爬坡事件的状态表征量，受预测水平限制，爬坡事件预测结果具有较强的不确定性，体现为风电爬坡事件的各个表征量的不确定性。基于非序贯蒙特卡罗模拟法的风电功率爬坡事件模型及与之相适应的常规机组停运模型如下所示。

1.1 风电功率爬坡事件模型

风电功率爬坡事件包括正爬坡和负爬坡，正爬坡可通过风机减载和停运加以控制，对系统影响较小。本文只考虑风电功率发生负爬坡的情况。爬坡事件日前预测精度较低，电网日前调度计划所依据的风电出力曲线由常规预测方法得出［4］。

在风电功率爬坡事件的建模过程中，忽略爬坡事件发生过程中的小幅功率波动，假设爬坡事件发生前和结束后，风电场预测出力与日前预测结果一致。综上所述，建立风电爬坡事件时序模型，如式（1）所示。

其中，Ts为爬坡事件的开始时间；Td为爬坡事件的持续时间；Pamp为爬坡事件的幅值，其反映了极端气象事件的影响范围，为更为直观地反映爬坡事件严重程度，本文将 Pamp用 0～100% 表示；PW（t）和 PW，0（t）分别为 t时刻的风电场实际出力和日前预测值；ΔPW，err（t）为t时刻风电功率预测误差，本文通过抽样得出。

风电功率爬坡事件预测结果通常用概率分布来表示［8］，爬坡事件的 3 个表征量 Ts、Td和 Pamp的概率分布分别为 p（Ts）、p（Td）和 p（Pamp），3 个表征量的期望及概率分布由风电爬坡事件预测系统提供。3个表征量相互独立，模拟风电功率爬坡事件时需对3个表征量按照相应的概率分布分别进行抽样。

1.2 考虑时序特性的常规机组停运模型

调度计划执行过程中发电机可能需要多次投入或退出运行，因此，发电机可靠性参数除与时间有关外还与投运成功率有关。常规机组的修复时间一般大于风险评估周期（本文取24 h），可将常规机组看作不可修复元件。机组i在t时刻处于停运状态的概率 pi（t）如式（2）所示［13］，等号右端第一项为机组投运失败的概率，第二项为机组投运成功的情况下在t时刻处于停运状态的概率。

其中，pi，UP和 λi分别为机组i的启动成功率和故障率；Δti为截止到 t时刻机组 i的持续运行时间；ti，on和ti，off分别为机组i的计划启动和停运时刻。

常规机组停运与风电出力爬坡事件相互独立，两者同时发生时对系统的影响最大，风险评估过程中应考虑常规机组停运与风电功率爬坡事件的时序关系。因此，适用于风电功率爬坡事件风险评估过程的常规机组停运模型应同时包含停运时刻和停运概率2个表征量。模拟常规机组停运过程时需对常规机组可能停运时刻和该时刻的停运情况分别进行抽样，抽样过程中两者所遵循的概率分布分别如式（3）和（4）所示。

其中，ti为机组 i的可能停运时刻；p′i（ti）的物理意义为若机组i在投运后发生停运，则停运事件发生在ti时刻的概率；p″i（ti）为机组 i在 ti时刻的等效停运概率；λ′i为机组 i的等效故障率。

机组i的等效故障率λ′i的构造原理如下：假设抽样次数为N，按式（2），机组i在ti时刻处于停运状态的样本数为 Ni=Npi（ti）；在考虑机组停运时刻后，N次抽样中机组 i投运失败的样本数为 Ni，1=Np″i（ti，on），投运成功的前提下，机组i在ti时刻处于停运状态的样本数 Ni，2如式（5）所示，数值上应等于 Ni-Ni，1，由此得到λi′。

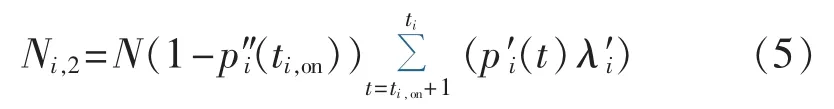
常规机组停运状态模拟过程为：首先抽样ti，on时刻机组 i运行状态表征量 ui（ti，on）（正常运行时为 1，否则为 0），若 ui（ti，on）为 1，抽样得到 ti，然后按式（4）中的 p″i（ti）抽样 ti时刻机组 i的运行状态 ui（ti）；对于在评估周期一开始便处于运行状态的机组则可直接抽样得出 ti及 ui（ti）。

1.3 运行风险指标

风电功率爬坡事件以及常规机组停运均会导致系统有功出力大幅变化，反映在电网侧为系统频率变化，当系统频率偏差超过限值且持续一段时间无法恢复时会引起低频减载装置动作。为准确分析风电功率爬坡事件对系统运行风险的影响程度，便于调度人员根据风险可接受程度（频率越限、失负荷等）采取相应控制措施。本文采用频率越限次数期望ENFO（Expected Number of Frequency Off-limits）和电力不足期望EENS（Expected Energy Not Supplied）作为风险指标，如式（6）、（7）所示［14］。

其中，ENFO和EENS分别为频率越限次数和电力不足期望；K 为蒙特卡罗抽样次数；T 为评估周期；IFO，k（t）为第k次抽样t时刻系统频率越限标识，发生频率越限或失负荷时取 1，否则为 0；ENS，k（t）为第 k 次抽样 t时刻系统失负荷量。

1.4 约束条件

（1）有功平衡约束：

其中，PW（t）和 PG，i（t）分别为 t时刻风电场和常规机组 i的有功出力；PL（t）为 t时刻负荷功率。

（2）发电机输出功率约束：

其中，PG，i，min和 PG，i，max分别为常规机组 i的最小和最大输出功率。

（3）常规机组爬坡速率约束：

其中，Ri，s为机组 i的输出功率改变速率（MW/min）；t1为一个评估时段。

2 爬坡事件作用下系统运行风险计算过程

2.1 风险指标的求取

爬坡事件作用下系统风险评估过程中第k次蒙特卡罗抽样所需变量为：爬坡事件表征量（Ts，Td，Pamp）、未发生爬坡事件时刻的风电出力预测误差ΔPW，err（t）和各常规机组停运状态表征量

本文以15 min作为一个评估时段，评估周期为24 h。风电功率爬坡事件与常规机组停运均会导致系统频率下降，需要常规机组增出力以满足有功平衡，与t时段相比，t+1时段系统有功调节容量需求dPr（t+1）和可调容量上限 dPup（t+1）分别如式（11）、（12）所示，其中 t1取 15 min。

风电功率爬坡事件会持续多个评估时段，在爬坡事件和常规机组停运共同作用下，为保证系统有功平衡，正常运行状态下的常规机组出力会大幅偏离计划值。 由式（11）、（12），对 t+1 时段进行风险评估时除需确定风电和负荷功率外，还需确定t时段结束后各常规机组的实际出力。为更为客观地反映爬坡事件作用下系统运行风险水平，并避免调度人员主观经验对评估结果的影响，本文不考虑再调度过程。调度时段内，常规机组（假设均为AGC机组，即可提供备用容量）除执行调度指令外，还需通过响应系统频率变化的方式分配系统有功不平衡量，下面分2种情况描述t时段结束后各常规机组出力求取原理。

（1）dPr（t）≤dPup（t），此时 t1时间内系统可调容量满足有功调节需求，该时段各项风险指标均为0。各常规机组按照固定的参与因子分配系统有功不平衡量［15］，其原理如式（13）所示。

其中，PG，i，ref（t）和 P′G，i（t）分别为 t时段机组 i出力计划值和考虑AGC调节作用时的目标出力；dPref（t）为忽略负荷预测误差情况下常规机组需比计划增发的总功率；αi为机组 i参与因子；ui，0（t）为 t时段机组 i的计划运行状态。

然后，校验式（13）所得结果是否满足爬坡和出力限值约束，若满足，则 PG，i（t）=P′G，i（t）；若 P′G，i（t）不满足上爬坡或出力上限约束，则 PG，i（t）如式（14）所示，并将越限量 P′G，i（t）-PG，i（t）分配至其他机组，直到所有机组满足约束。

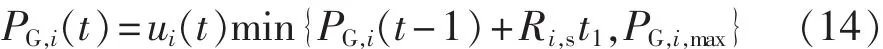
（2）dPr（t）＞dPup（t），此时各常规机组出力如式（14）所示，对应的系统功率缺额 ΔP（t）=dPr（t）-dPup（t），常规机组调节能力已达到上限，系统可能会发生频率越限或失负荷［16］。本文采用准稳态模型估计系统频率偏差［17］，系统频率偏差 Δf估计值如式（15）所示，当Δf超过限值 Δflim时 IFO，k（t）取 1，并在频率低于 fL，shed（低频减载装置动作频率）时计算减载量ENS，k（t）［13，17］。

其中，fN为系统额定频率；KL为负荷的频率调节效应系数；PLN（t）为t时段系统在额定频率下的负荷功率。

2.2 风险评估流程

上节描述了风险指标的求取原理，风险评估的具体步骤如下。

a.输入常规机组出力计划、风电和负荷日前预测曲线。

b.输入爬坡事件预测结果：Ts、Td和Pamp的概率分布。

c.抽样得到风电出力爬坡事件表征量和未发生爬坡事件时刻的风电出力预测误差，并据此得到风电出力曲线。

d.抽样得到常规机组停运状态表征量。

e.求取本次抽样的风险指标和

f.返回步骤c，进行下一次抽样计算，直到满足误差允许范围或达到迭代次数限值。

前面描述了风电功率爬坡事件作用下系统运行风险评估的过程，具体流程如图1所示。

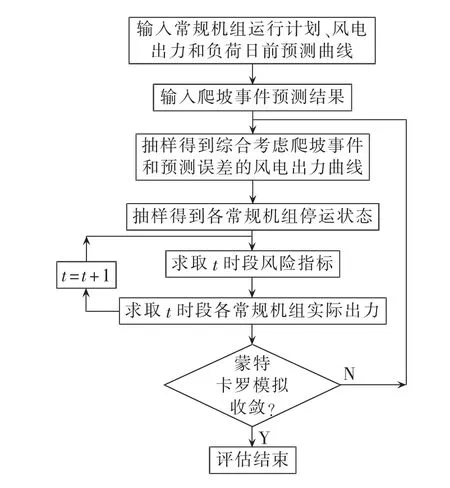
图1 风电功率爬坡事件风险评估流程Fig.1 Flowchart of risk assessment for wind power ramp event

3 算例分析

采用IEEE RTS 24节点系统来验证本文模型，模型结构图如图2所示。该系统总装机容量为3405 MW，负荷峰值为2850 MW。将系统中26号机组替换为一容量400MW的风电场，风电渗透率约为15%。常规机组参数、负荷数据以及日发电计划取自文献［18-19］，系统中低频减载装置参数设定取自文献［13］。假设风电功率爬坡事件开始时间在0～24 h内服从均匀分布（电网实际运行中可通过风电功率爬坡事件预测系统得到），爬坡持续时间和爬坡量采用文献［12］中的统计结果，风电出力数据来源于山东某风电场日前预测数据。

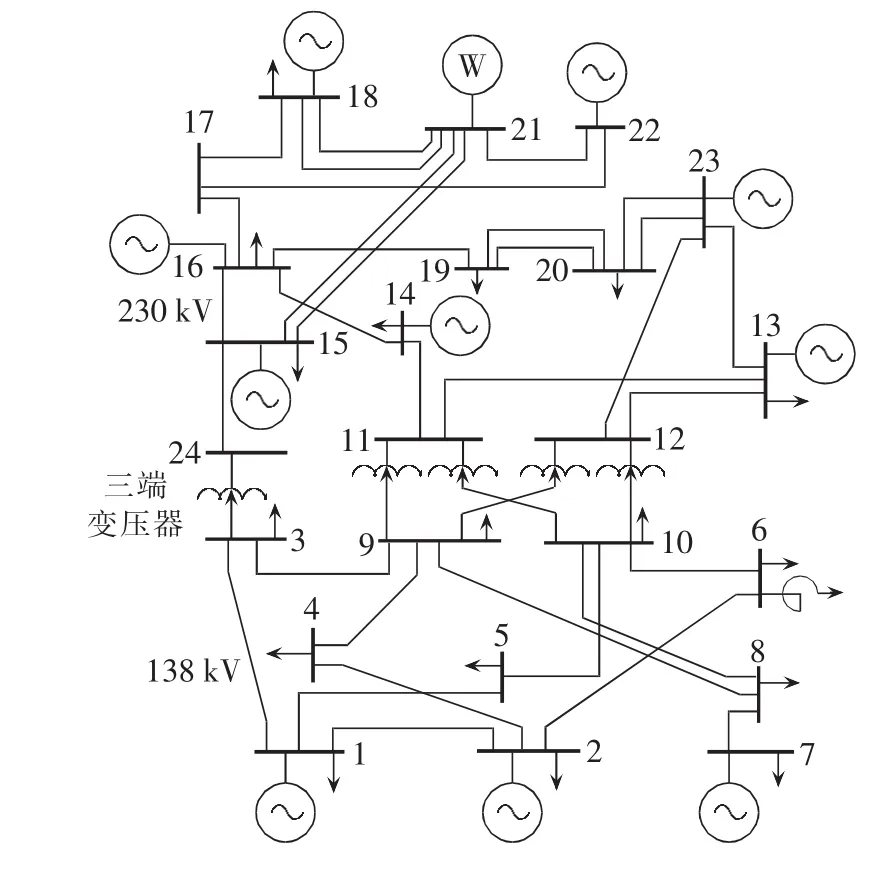
图2 含风电场的测试系统Fig.2 Test system with wind farm

3.1 常规机组停运模型有效性分析

为验证本文所提模型有效性，对传统的单时段风险评估方法（各评估时段之间相互独立，常规机组停运概率参照式（2））和本文所提考虑时序特性的风险评估方法分别进行仿真分析，仿真过程中风电和负荷曲线均取日前预测值，2种不同的评估方法计算结果如图3、4和表1所示，图中括号内数据表示相应曲线所对应纵坐标需乘以的系数，后同。

图3 单时段风险评估方法计算结果Fig.3 Calculated results by single-period risk assessment method

图4 考虑时序特性的风险评估方法计算结果Fig.4 Calculated results by risk assessment method considering time-sequence characteristics

表1 不同风险评估方法结果对比（Pamp=0）Table 1 Comparison of simulative results between risk assessment methods（Pamp=0）

从图3、4和表1可以看出，在无风电功率爬坡事件发生情况下，本文所提考虑时序特性的风险评估方法与传统单时段风险评估方法结果基本一致，证明了本文所提模型的有效性。

3.2 爬坡事件与常规机组停运之间的时序关系对评估结果的影响分析

假设（Ts，Td，Pamp）取值为（7，2.5，50%），选择 19号机组为测试机组，除19号机组外其他机组均不发生计划外停运，19号机组停运时刻分别为1～24 h时计算系统的ENFO和EENS，结果如图5所示。

从图5中可以看出，常规机组停运发生在1～6 h时，无失负荷或频率越限情况发生，而停运事件发生在时段7～9.5 h时，系统存在较大的运行风险。发电vs.generator outage time机停运发生在第6 h或第7 h时，在第7 h处于运行状态的常规机组需比计划值增发的总功率是相同的，而在第7～9.5 h，常规机组在应对负荷增加和风电功率爬坡事件所造成的有功缺额过程中，有功出力调节速率已接近上限，但距离最大输出功率（额定功率）仍有较大裕度，在无常规机组停运情况下，不发生失负荷；若发生常规机组停运，则大幅增加了常规机组有功调节速率需求，造成失负荷。若常规机组停运发生在爬坡事件之前，在爬坡事件发生时，常规机组停运所造成的有功缺额已由系统备用所补偿，未增加爬坡事件发生过程中的常规机组有功出力调节速率需求，且由于可调容量充足，无失负荷情况发生。当常规机组停运发生在爬坡事件结束之后时（10～24 h），无失负荷情况发生。

图5 系统风险指标随机组停运时刻的变化曲线Fig.5 Curves of system risk index

假设19号机组在各评估时段停运概率均为10-4，爬坡事件表征量（Ts，Td，Pamp）仍取（7，2.5，50%），分别采用单时段风险评估方法和本文所提考虑时序特性的风险评估方法评估系统运行风险，结果如图6、7和表2所示。

图6 单时段风险评估方法计算结果Fig.6 Calculated results by single-period risk assessment method

图7 考虑时序特性的风险评估方法计算结果Fig.7 Calculated result by risk assessment method considering time-sequence characteristics

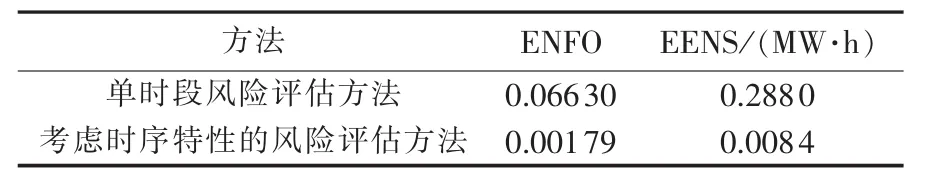
表2 不同风险评估方法结果对比（Pamp=50%）Table 2 Comparison of simulative results between risk assessment methods（Pamp=50%）

对比图6、7和表2可以看出，爬坡事件发生情况下，单时段评估方法计算结果明显大于考虑时序特性的风险评估结果，原因如下：在抽样次数足够多的情况下，2种方法抽样得出的19号机组在各时段处于停运状态的样本数相同，其他机组有功出力调节目标也相同（如式（13）所示），即与计划值相比，处于正常运行状态的机组所需增发的总功率包括常规机组停运和风电功率爬坡所造成的功率缺额。但2种方法在计算各时段风险指标时所参照的有功调节需求不同。以第9 h为例，单时段风险评估方法不考虑时段之间的关联性，计算有功调节需求时以计划值为基准，抽样第9 h处于停运状态的样本时所参照的概率分布（式（2））包含了第9 h之前出现常规机组停运的概率（式（2）为处于停运状态的概率，而不是在该时段发生停运的概率），增大了评估过程中常规机组停运与爬坡事件同时发生的样本数；再者，单时段评估方法所参照的爬坡事件所造成的有功缺额为而实际上在第9 h由爬坡事件所造成的有功冲击为?（第 8h 到第 9h 之间爬坡量），dPW，1明显大于 dPW，2。

3.3 爬坡事件作用下系统运行风险分析

风电功率的爬坡幅值代表了爬坡事件的严重程度，不同的爬坡幅值作用下，计算测试系统的风险指标ENFO和EENS，结果如图8所示。

图8 系统风险指标随爬坡幅值的变化曲线Fig.8 Curves of system risk index vs.ramp amplitude

从图8中可以看出，在Pamp＜30%时，系统各项风险指标基本不变，原因是，此时系统备用容量较为充足。随着Pamp继续增大，ENFO先开始明显增加，原因是系统内常规机组虽然在某些时段出现调节能力不足的情况，但还不足以触发低频减载。在Pamp大于45%左右时，EENS开始增加，且增加的速率明显大于ENFO，原因是在发生失负荷时，系统内各机组的调节能力已达到限值，此时，EENS会随Pamp的增大而迅速增大；而ENFO最大值要小于爬坡事件影响的时段数。

为进一步分析系统在不同运行状态下，风电功率爬坡事件对系统运行风险的影响，计算Pamp取值为100%时系统各时段风险指标，图9为系统风险指标变化曲线。

图9 Pamp为100%时系统风险指标的变化曲线Fig.9 Curves of system risk index for Pamp=100%

从图4和图9中可以看出，系统运行风险变化趋势与负荷水平总体相同。如在负荷水平较低的时段第1～5 h，对应的风险水平较低；而在负荷水平较高的时段第10～20 h，系统风险水平较高，原因是负荷水平较高时系统内常规机组出力水平较高，可用上调容量相对较小。负荷水平相同的情况下，系统运行风险也有所差异，如第24 h与第1～2 h负荷水平差别不大，且计划投运的机组完全相同，但第24 h风险水平要高于第1～2 h，原因是常规机组在第24 h处于停运状态的概率要高于第1～2 h，相应的风险水平较高。

由于仿真中对风电功率爬坡事件开始时间进行抽样时采用的是均匀分布，图9中各时刻发生爬坡事件的样本数相同。在负荷曲线、常规机组停运率以及日发电计划确定的情况下，爬坡事件开始时间不同，对系统运行风险的影响存在较大差异。各时段系统运行风险水平除与负荷水平相关外，还与负荷变化方向有关。当爬坡事件与负荷攀升同时发生时，如时段第8～11 h，爬坡事件对系统风险水平的影响尤为明显，原因是当爬坡事件与负荷攀升同步时，两者作用叠加，增大了净负荷变化量、变化速率以及系统备用需求，造成系统风险指标的增大，该场景与美国德克萨斯州电网2007年和2008年发生的2次造成严重影响的风电爬坡事件相类似［3-4］。当爬坡事件与负荷下降过程同时发生时，对系统运行风险的影响较小，如时段第22～24 h，原因是当爬坡事件与负荷下降过程同步时，风电功率与负荷同步下降，两者作用抵消，净负荷变化量较小，相应的备用需求较小。

4 结论

本文提出一种风电功率爬坡事件作用下考虑时序特性的系统风险评估模型，通过对常规机组可能停运时间和运行状态分别进行抽样，考虑了爬坡事件与常规机组间的时序关系对评估结果的影响。评估过程中考虑时段之间的关联性，在计及低频减载及AGC调节作用的基础上通过频率越限次数期望和失负荷的期望对系统运行风险进行了评估，量化了爬坡事件对系统运行风险的影响程度，可为调度人员根据风险接受程度采取预防控制措施提供指导，具有实际应用参考价值。

［1］张里，刘俊勇，刘友波，等.计及风速相关性的电网静态安全风险评估［J］.电力自动化设备，2015，35（4）：84-89.ZHANG Li，LIU Junyong，LIU Youbo，et al.Static security risk assessment of power system considering wind speed correlation［J］.Electric Power Automation Equipment，2015，35（4）：84-89.

［2］KAMATH C.Associating weather conditions with ramp events in wind power generation［C］∥IEEE PES Power Systems Conference and Exposition（PSCE）.Phoenix，Arizona：［s.n.］，2011：1-8.

［3］戚永志，刘玉田.风电高风险爬坡有限度控制［J］.中国电机工程学报，2013，33（13）：69-75.QI Yongzhi，LIU Yutian.Finite control of high risk wind power ramping［J］.Proceedings of the CSEE，2013，33（13）：69-75.

［4］ELA E，KIRBY B.ERCOT event on February 26，2008：lessons learned［R］.Golden，Colorado：NREL，2008.

［5］WAN Yihhuei.Analysis of wind power ramping behavior in ERCOT［R］.Golden，Colorado：NREL，2011.

［6］GREAVES B，COLLINS J，PARKES J，et al.Temporal forecast uncertainty for ramp events［J］.Wind Engineering，2009，33（4）：309-319.

［7］OUYANG Tinghui，ZHA Xiaoming，QIN Liang.A survey of wind power ramp forecasting［J］.Energy and Power Engineering，2013，5：368-372.

［8］ZACK J W，YOUNG S，COTE M，et al.Development and testing of an innovative short-term large wind ramp forecasting system［C］∥Proceedings of the European Wind Energy Conference ＆Exhibition.Warsaw，Poland：［s.n.］，2010：1-10.

［9］吴林伟，张建华，刘若溪.考虑风电机组故障的风电场可靠性模型及其应用［J］.电力系统自动化，2012，36（16）：31-35.WU Linwei，ZHANG Jianhua，LIU Ruoxi.A wind farm reliability model considering wind turbine faults and its application ［J］.Automation of Electric Power Systems，2012，36（16）：31-35.

［10］张宏宇，印永华，申洪，等.大规模风电接入后的系统调峰充裕性评估［J］.中国电机工程学报，2011，31（22）：26-31.ZHANG Hongyu，YIN Yonghua，SHEN Hong，et al.Peak-load regulation adequacy evaluation associated with large wind power integration［J］.Proceedings of the CSEE，2011，31（22）：26-31.

［11］姚瑶，于继来.计及风电备用风险的电力系统多目标混合优化调度［J］.电力系统自动化，2011，35（22）：118-124.YAO Yao，YU Jilai.Multi-objective hybrid optimal dispatch of power systems considering reserve risk due to wind power［J］.Automation of Electric Power Systems，2011，35（22）：118-124.

［12］SEVLIAN R，RAJAGOPAL R.Detection and statistics of wind power ramps［J］.IEEE Transactions on Power Systems，2013，28（4）：3610-3620.

［13］王成亮，赵渊，周家启，等.基于日发电计划的电力系统运行风险概率评估［J］.电力系统自动化，2008，32（4）：6-10.WANG Chengliang，ZHAO Yuan，ZHOU Jiaqi，et al.Probabilistic evaluation of power system operational risk based on daily generation scheduling［J］.Automation of Electric Power Systems，2008，32（4）：6-10.

［14］赵晋泉，唐洁，罗卫华，等.一种含风电电力系统的日前发电计划和旋转备用决策模型［J］. 电力自动化设备，2014，34（5）：21-27.ZHAO Jinquan，TANG Jie，LUO Weihua，etal.Day-ahead generation scheduling and spinning reserve decision-making model for power grid containing wind power［J］.Electric Power Automation Equipment，2014，34（5）：21-27.

［15］蒋哲，韩学山，王孟夏.伴随AGC机组控制过程的潮流模型与算法［J］. 电网技术，2010，34（1）：68-72.JIANG Zhe，HAN Xueshan，WANG Mengxia.Model and algorithm for power flow accompanying with automatic generation control process［J］.Power System Technology，2010，34（1）：68-72.

［16］刘新东，江全元，曹一家，等.基于风险理论和模糊推理的电力系统暂态安全风险评估［J］. 电力自动化设备，2009，29（2）：15-20.LIU Xindong，JIANG Quanyuan，CAO Yijia，et al.Transient security risk assessment of power system based on risk theory and fuzzy reasoning［J］.Electric Power Automation Equipment，2009，29（2）：15-20.

［17］崔明建，孙元章，柯德平，等.考虑电网侧频率偏差的风电功率爬坡事件预测方法［J］. 电力系统自动化，2014，38（5）：8-13.CUIMingjian，SUN Yuanzhang，KE Deping，etal.Prediction method for wind power ramp events considering frequency deviation of power grid side［J］.Automation of Electric Power Systems，2014，38（5）：8-13.

［18］WANG C，SHAHIDEHPOUR S M.Ramp-rate limits in unit commitment and economic dispatch incorporating rotor fatigue effect［J］.IEEE Transactions on Power Systems，1994，9（3）：1539-1545.

［19］初壮，于继来.初期电力市场确定电网日发电计划的模型与方法［J］. 电力系统自动化，2006，30（22）：43-47.CHU Zhuang，YU Jilai.Model and method for daily dispatch scheduling in primary power markets［J］.Automation of Electric Power Systems，2006，30（22）：43-47.