基于过渡电阻倾斜角的光伏并网自适应距离保护

张 尧 ，晁 勤 ，李育强 ，王一波

（1.新疆大学 电气工程学院，新疆 乌鲁木齐 830046；2.新疆工程学院，新疆 乌鲁木齐 830091）

0 引言

随着光伏发电技术的日趋成熟，全国各地大容量的光伏电站并网项目逐一投运，光伏电站升压接入110 kV电网成为一种普遍现象。光伏电站升压并入110 kV电网使经过渡电阻接地距离保护测量阻抗不能准确反映故障点的位置。

现有关于光伏电站并网对保护影响的研究，主要集中在对电流保护的影响和应对措施方面［1-8］，对距离保护的影响研究较少。对于双电源供电系统经过渡电阻接地距离保护测量阻抗偏离实际值问题的解决方法有很多［9-14］。文献［9］对测量电抗的误差进行实时估算，根据误差的正负来确定是否补偿，从而得到自适应接地距离继电器动作判据，既防止了距离保护超越误动，又扩大了距离保护的动作范围。文献［10］通过对阻抗变化轨迹的估算，提出了一种基于自适应电抗元件的四边形距离继电器的原理及实施方案，可有效防止区外经过渡电阻故障时的超越，同时区内故障耐受过渡电阻的能力增强。文献［11］基于故障前电源电势与负荷电流之间的相位关系合理地估计对侧电源阻抗角，利用传统距离保护测量阻抗的电抗、电阻分量与正序电流分支系数的相角之间的增减关系分别提出了防止保护拒动和超越的解决办法。文献［12］通过将双端电源系统的故障过渡电阻分解为2个不同电阻的并联得到2个相对独立的单端电源故障系统的组合，并测量保护安装处的有功功率补偿故障过渡电阻对接地距离保护的影响。

但是，这些文献都没有从过渡电阻倾斜角变化角度研究探讨。因双电源供电系统经过渡电阻短路后过渡电阻Rf呈容性或者感性，具有倾斜角，但传统算法不考虑倾斜角的变化；当加入光伏电站后仍然采用传统算法，没有计及倾斜角随光强变化的特性，造成距离保护不能正确动作。因此，本文提出一种基于过渡电阻倾斜角估计的自适应距离保护。通过故障分量分析发现过渡电阻倾斜角θ完全由光伏电站的等效阻抗XN决定，而光伏电站的等效阻抗XN随着光伏电站发电量P的变化而变化。进一步分析网侧发生接地故障时光伏电站的短路电压、短路电流的规律，采用最小二乘法估算出光伏电站的发电量P与等效阻抗XN间的关系，进而采用相量图获得过渡电阻倾斜角θ变化引起的测量阻抗误差ΔZm与光伏电站的发电量P间的关系并给出距离保护判据，最终实现了基于过渡电阻倾斜角估计的光伏并网自适应距离保护。通过仿真分析，该方法比传统的计算方法更准确，误差由14%减至2.4%，极大地减小了过渡电阻对光伏并网距离保护测量阻抗的影响。

1 基于故障分量建立过渡电阻倾斜角θ与光伏电站等效阻抗XN间的关系

1.1 过渡电阻倾斜角θ的定义

光伏电站并网系统如图1所示，在线路K点发生经过渡电阻接地短路故障，设母线M处的故障电压分量为ΔuM，两侧母线流向短路点K的故障电流分量分别为ΔIM和ΔIN，流过过渡电阻Rf的故障电流分量为ΔIf。

母线M处的故障电压分量ΔuM为：

图1 光伏电站并网系统图Fig.1 Schematic diagram of grid-connected PV station system

其中，ΔIM0为 ΔIM的零序分量；Z1、Z0分别为线路的正序和零序阻抗。

测量阻抗Zm为：

由过渡电阻引起的测量阻抗误差ΔZm为：

ΔZm的夹角即为过渡电阻倾斜角θ。

1.2 故障分量建模

图1对应的系统经过渡电阻单相接地短路故障分量等效网络如图2所示，设短路点K与母线M相距 y（单位 km），母线 M、N 相距 l（单位 km），rL、xL分别为输电线路单位电阻和电抗，XM、XN分别为M、N侧母线背后的系统电抗。

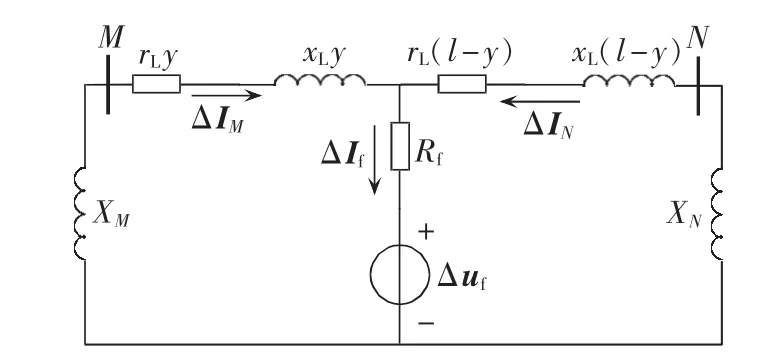
图2 系统故障分量等效网络Fig.2 Equivalent network of system fault components

图2和式（3）中的 ΔIM和 ΔIM0都是可测的；ΔIf是未知量，但是可以求出ΔIf与ΔIM之间的夹角。令α为ΔIf与ΔIM之间的夹角：

那么ΔIf可以表示为：

其中，k为未知量；α可以通过式（4）求得。

1.3 θ、XN间关系推导

将式（5）代入式（3）可得式（6）：

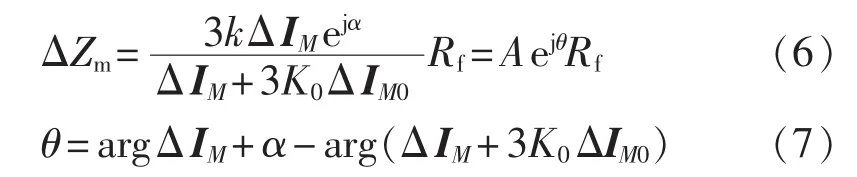
其中，A 表示的幅值，由于k是未知量，所以A也是未知量。

由式（7）可知，θ与α密切相关，α受M、N两侧系统的阻抗影响，M侧系统的等效阻抗不变，而N侧系统即光伏电站的等效阻抗XN实时变化，由此获得过渡电阻倾斜角θ与光伏电站等效阻抗XN间关系。

2 基于最小二乘法建立光伏电站发电量P与等效阻抗XN的关系

光伏电站发电量P主要受日照强度和温度的影响，而其直接影响光伏电站等效阻抗XN。由于光伏电站发电量P实时可测，找出其与光伏电站等效阻抗XN之间的关系是确定过渡电阻倾斜角θ的关键。

2.1 光伏电站短路电压、电流变化特性分析

由不同光照强度光伏模块的电流电压特性曲线［15］可知，不同光照强度下的开路电压不同，随着光照强度的减弱，开路电压也随之减小。而光伏电站交流侧的输出电压基本是恒定的，由于采用具有最大功率跟踪功能的逆变装置，统计显示光伏组件等效阻抗的端电压最大不超过实时输出电压的20%，所以本文按DC/AC直流侧实时输入电压的20%来模拟电网短路时直流侧最大可升高的电压［16］。

采用仿真软件搭建图1所示新疆某实际电网模块，并设定在1 s时刻K点发生单相接地故障，经0.1 s故障被切除，电网恢复正常运行。光伏电站交流侧电流变化曲线如图3所示，图中电流I为标幺值。

图3 电网故障下光伏电站电流变化曲线Fig.3 Current variation of PV station when grid fault occurs

从图3可以看出，网侧发生故障时光伏发电电流突增，在故障存在期间（1～1.1 s内）电流被限制为1.2倍的额定电流。在故障结束后，光伏发电电流能够逐渐恢复至故障前的水平。这一过程和实际光伏电站逆变器响应特性一致。所以本文按实时输出电流的120%来模拟短路时交流侧最大可升高的电流。

2.2 最小二乘法建立XN-P关系模型

一组光伏组件+逆变器的等效阻抗XN′可由电网短路时直流侧最大可升高的电压与交流侧最大可升高的电流的比值来近似，最后根据各组光伏组件+逆变器的等效阻抗并联来求光伏电站的等效阻抗XN。

光伏电站装机容量为10 MW时，将由20组光伏组件+逆变器的等效阻抗组成，并联后折算至35 kV侧可得光伏电站等效阻抗，光伏电站发电量P与等效阻抗XN的对应值如表1所示。

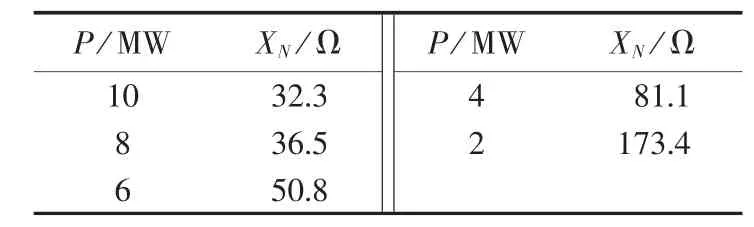
表1 光伏发电量P与等效阻抗XN的对应值Table 1 Power generating capacity P and corresponding equivalent impedance XN

在直角坐标系上取光伏电站发电量P为横坐标、光伏电站等效阻抗XN为纵坐标，描出表1各组数据的对应点并连线，如图4所示。

图4 XN-P变化曲线Fig.4 Curve of XNvs.P

从图4中可知，这些点的连线类似于幂函数，可以设XN=f（P）=bPa，其中a和b是待定常数。利用最小二乘法来确定光伏电站发电量P与光伏电站等效阻抗XN之间满足的关系式。

设函数F：

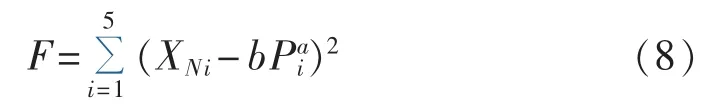
对函数F分别求a和b的偏导：

求出光伏电站发电量P与等效阻抗XN满足的函数关系式如下：

3 自适应距离保护的实现

3.1 运用相量图获取线路短路阻抗Zd

测量阻抗Zm根据式（2）可以获得，在第2节确定了过渡电阻倾斜角θ后，可以运用相量图的方法，获得线路短路阻抗Zd。具体步骤如下：

a.已知测量阻抗Zm，在相量图中画出Zm；

b.过测量阻抗Zm画水平线，通过第2节可得到过渡电阻倾斜角θ，然后画出与该水平线夹角为θ的矢量定义为ΔZm；

c.已知线路阻抗角β，并画出该矢量，与矢量ΔZm相交，定义为Zd，Zd表示线路短路阻抗。

图5给出了2种情况。当θ＞0°时，如图5中θ2所示，ΔZm2是向上倾斜并指向Zm，此时线路短路阻抗为 Zd2。 当 θ＜0°时，如图 5 中 θ1所示，ΔZm1是向下倾斜并指向Zm，此时线路短路阻抗为Zd1。

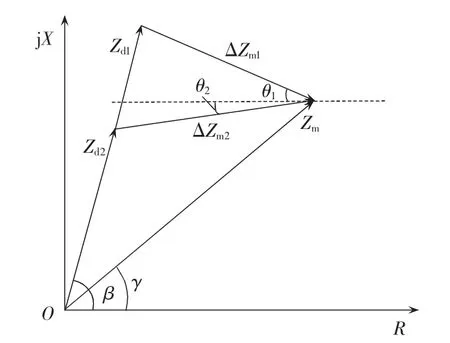
图5 求线路短路阻抗的相量图Fig.5 Phasor diagram for obtaining line short circuit impedance

图6为光伏电站并入系统联络线上的某一点经过渡电阻单相接地短路时，过渡电阻倾斜角θ随光伏电站发电量P的变化情况。当光伏电站发电量为P1时，过渡电阻倾斜角为θ1。当光伏电站发电量为 P2（P2＞ P1）时，过渡电阻倾斜角为 θ2。 由图 6 可知，θ2＞θ1，即随着光伏发电量 P 的增大，过渡电阻倾斜角也在顺时针增大。

图6 过渡电阻倾斜角θ的变化Fig.6 Variation of transition resistance tilt angle θ

3.2 自适应距离保护判据

根据距离保护原理和图5可知，自适应距离保护动作判据为式（11）：

其中，Zset为整定阻抗。

根据三角函数正弦定理可得：

其中，γ为测量阻抗角，即Zm与R轴的夹角，为已知量。将式（12）代入式（11），自适应距离保护动作判据为式（13）：

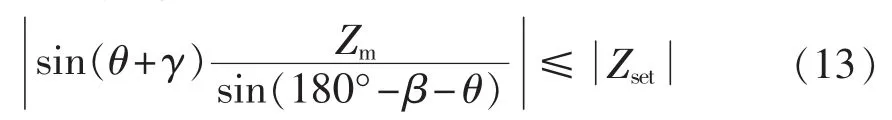
3.3 本文算法与传统算法的区别

传统算法不考虑光伏电站发电量P变化的影响和过渡电阻倾斜角θ的变化，依据式（2），在测得ΔuM、ΔIM、ΔIM0后即可求解得到 Zm并代入传统距离保护动作判据，造成测距误差较大。

本文算法考虑光伏电站发电量P变化的影响和过渡电阻倾斜角θ的变化，在线确定光伏电站发电量P，对传统算法求出的Zm进行了修正，减小了测距误差。

4 仿真分析与验证

仿真算例采用图1所示的网架结构，10 MW的光伏电站通过110 kV联络线并入系统，利用PSCAD进行仿真，系统M侧的参数分别为正序阻抗zM1=2.251+j43.15 Ω，零序阻抗 zM0=j21.69 Ω；线路参数为正序电阻 rL1=0.105 Ω /km，正序电抗 xL1=1.258 Ω /km，零序电阻 rL0=0.315 Ω /km，零序电抗 xL0=3.774 Ω /km；线路长度为 100 km。

表2—5分别给出了不同光伏电站装机容量和不同过渡电阻值情况下传统算法和本文算法的接地距离保护仿真计算结果，故障类型为单相接地故障，Lf和Lfm分别为实际故障距离和故障距离测量结果。

表2 P=10 MW、Rf=10 Ω时的仿真结果Table 2 Simulative results when P=10 MW and Rf=10 Ω

表3 P=10 MW、Rf=50 Ω时的仿真结果Table 3 Simulative results when P=10 MW and Rf=50 Ω

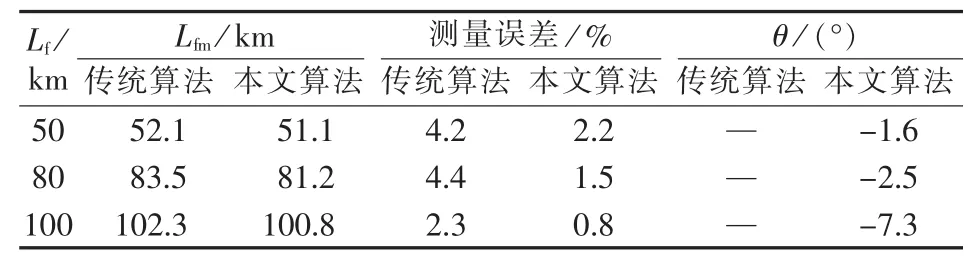
表4 P=5 MW、Rf=10 Ω时的仿真结果Table 4 Simulative results when P=5 MW and Rf=10 Ω

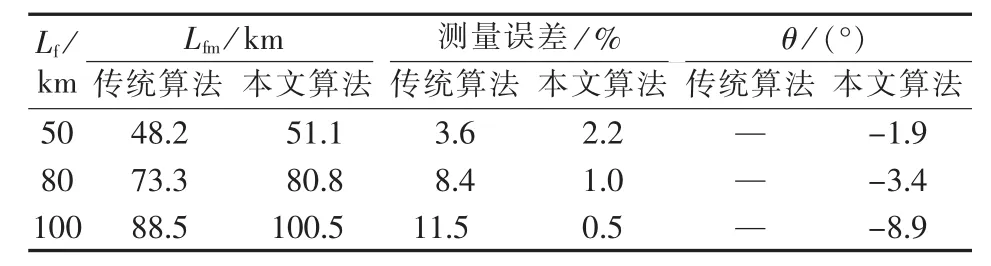
表5 P=5 MW、Rf=50 Ω时的仿真结果Table 5 Simulative results when P=5 MW and Rf=50 Ω

由表2—5可以得出以下结论。

a.经相同过渡电阻接地时，随着光伏电站发电量P的增大，传统算法的结果会变小，而本文的算法基本不受光伏电站发电量P变化的影响。

b.在光伏电站发电量P一定的情况下，传统算法会随着过渡电阻的增大明显减小，有可能使保护误动，而本文算法不受过渡电阻的影响，计算结果比较接近于真实值。

c.传统算法最大误差可达14%，本文算法最大误差为 2.4%。

d.Rf=10 Ω时，光伏电站发电量P从5 MW变化至10MW，过渡电阻倾斜角θ的变化范围为-1.6°～-8.7°。 Rf=50 Ω 时，光伏电站发电量P从5 MW变化至10 MW，过渡电阻倾斜角θ的变化范围为-1.9°～-10.1°。

e.本文算法会因为光伏电站发电量P与其等效阻抗XN的估算关系存在一定误差，这是今后需要完善的地方。

5 结语

本文提出一种基于过渡电阻倾斜角估计的自适应距离保护算法，PSCAD仿真分析表明，该算法比传统的计算方法更准确，极大地减小了过渡电阻对光伏并网距离保护测量阻抗的影响。

［1］李斌，袁越.光伏并网发电对保护及重合闸的影响与对策［J］.电力自动化设备，2013，33（4）：12-17.LI Bin，YUAN Yue.Impact of grid-connected photovoltaic power generation on protection and reclose，and itscountermeasures［J］.Electric Power Automation Equipment，2013，33（4）：12-17.

［2］石振刚，王晓蔚，赵书强.并网光伏发电系统对配电网线路保护的影响［J］.华东电力，2010，38（9）：1405-1408.SHIZhengang，WANG Xiaowei，ZHAO Shuqiang.Influenceof grid connected photovoltaic power system on line protection of distribution network［J］.East China Electric Power，2010，38（9）：1405-1408.

［3］孙景钌，李永丽，李盛伟，等.含逆变型分布式电源配电网自适应电流速断保护［J］.电力系统自动化，2009，33（14）：71-76.SUN Jingliao，LI Yongli，LI Shengwei，et al.Study on adaptive currentinstantaneous trip protection scheme fordistribution network with inverter interfaced DG［J］.Automation of Electric Power Systems，2009，33（14）：71-76.

［4］张艳霞，代凤仙.含分布式电源配电网的馈线保护新方案［J］.电力系统自动化，2009，33（12）：71-74.ZHANG Yanxia，DAI Fengxian.New schemes of feeder protection for distribution networks including distributed generation［J］.Automation of Electric Power Systems，2009，33（12）：71-74.

［5］刘伟，彭冬，卜广全，等.光伏发电接入智能配电网后的系统问题综述［J］.电网技术，2009，33（19）：1-6.LIU Wei，PENG Dong，BU Guangquan，et al.A survey on system problems in smartdistribution network with grid-connected photovoltaic generation［J］.Power System Technology，2009，33（19）：1-6.

［6］庞建业，夏晓宾，房牧.分布式发电对配电网继电保护的影响［J］.继电器，2007，35（11）：5-8.PANG Jianye，XIA Xiaobin，FANG Mu.Impactofdistributed generation to relay protection of distribution system［J］. Relay，2007，35（11）：5-8.

［7］张保会，李光辉，王进，等.风电接入电力系统故障电流的影响因素分析及对继电保护的影响［J］. 电力自动化设备，2012，32（2）：1-8.ZHANG Baohui，LI Guanghui，WANG Jin，et al.Affecting factors of grid-connected wind power on fault current and impact on protection relay［J］.Electric Power Automation Equipment，2012，32（2）：1-8.

［8］贺家李，宋从矩.电力系统继电保护原理［M］.北京：中国电力出版社，2004：100-102.

［9］索南加乐，许庆强，宋国兵，等.自适应接地距离继电器［J］.电力系统自动化，2005，29（17）：54-58.SUONAN Jiale，XU Qingqiang，SONG Guobing，et al.Adaptive earth faultdistancerelay ［J］.Automation ofElectric Power Systems，2005，29（17）：54-58.

［10］沈冰，何奔腾.基于阻抗轨迹估计的自适应相间距离继电器［J］.中国电机工程学报，2007，27（31）：71-76.SHEN Bing，HE Benteng.A novel adaptive distance protection based on impedance locus estimation［J］.Proceedings of the CSEE，2007，27（31）：71-76.

［11］张华中，朱玲玲，张洪涛，等.基于估算对策电源阻抗的自适应距离保护算法［J］. 电力系统自动化，2011，35（12）：70-74.ZHANG Huazhong，ZHU Lingling，ZHANG Hongtao，et al.Adaptive distance protection algorithm based on estimation of contralateral source impedance［J］.Automation of Electric Power Systems，2011，35（12）：70-74.

［12］邹亮，李庆民，刘洪顺，等.计及故障限流器和故障过渡电阻的接地距离保护补偿算法［J］. 电力自动化设备，2009，29（3）：56-60.ZOU Liang，LIQingmin，LIU Hongshun，etal.Compensation algorithm of grounding distance protection considering FCL and fault resistance［J］.Electric Power Automation Equipment，2009，29（3）：56-60.

［13］PRADHAN A K，JOOS G.Adaptive distance relay setting for linesconnecting wind farms ［J］.IEEE Transon Energy Conversion，2007，22（1）：206-213.

［14］ANDERSON P M.Power system protection［M］. ［S.l.］：IEEE Press，1998：23-24.

［15］戴训江，晁勤.太阳能光伏模块电气特性的数学建模与仿真［J］.半导体光电，2009，30（1）：47-51.DAI Xunjiang，CHAO Qin.Mathematical model and simulatioin analysis ofphotovoltaic module electricalcharacteristics［J］.Semiconductor Optoelectronics，2009，30（1）：47-51.

［16］周林，张密，居秀丽，等.电网阻抗对大型并网光伏系统稳定性影响分析［J］. 中国电机工程学报，2013，33（34）：34-41.ZHOU Lin，ZHANG Mi，JU Xiuli，et al.Stability analysis of large-scale photovoltaic plants due to grid impedance［J］.Proceedings of the CSEE，2013，33（34）：34-41.