光伏并网附加控制抑制交流串补引起的次同步谐振

陈 实 ，李兴源，李 宽

（1.四川大学 电气信息学院，四川 成都 610065；2.国网山东省电力公司电力科学研究院，山东 济南 250002）

0 引言

太阳能因其分布广泛、可再生、不污染环境等优点，逐渐得到人们广泛关注，同时光伏发电也是缓解化石能源消耗与环境保护的有效发电方式，青海近两年光伏发电的规划已达8000 MW。为了提高光伏发电效率，国内外专家学者在太阳能光伏阵的最大功率点跟踪MPPT（Maximum Power Point Tracking）方面做了大量研究［1-3］。同时为了提高光伏并网效率与稳定性，大规模光伏发电并网影响分析成为当前研究重点。目前应用最广泛的并网控制方式为双闭环解耦控制策略［4-5］，也有大量研究提出利用无差拍控制、模糊控制、比例谐振控制与鲁棒控制等代替原有的PI控制方式［6-8］，以提高光伏并网的稳定性，光伏电站的稳定并网并具有较好的暂态特性也成为光伏发电亟待实现的目标。

交流输电系统中通常通过串补电容以提高输电线路的输送能力，但当串补系统发生扰动时，有可能引起次同步谐振SSR（SubSynchronous Resonance）。SSR是发电机组轴系与电网之间的一种能量放大现象，表现为机组轴系模块间的相互扭振，严重的SSR会造成发电机组轴系损坏乃至影响整个电网的安全稳定运行［9］。在SSR振荡模态的检测与抑制方面，已有大量的研究。目前研究较为成熟的振荡电气量检测方法是特征根分析法［10-12］。SSR的抑制方法多种多样，其中通过静止无功补偿器SVC（Static Var Compensator）［13-14］和附加励磁阻尼控制器 SEDC（Supplementary Excitation Damping Controller）［15］等方法发展较为成熟。随着新能源技术的发展，新能源并网时电力系统的次同步振荡问题越来越得到人们的关注。其中，文献［16］提出通过双馈风机并网，并在风电场主控制器上加附加控制器，抑制交流串补引起的SSR，并以次同步IEEE第二标准模型作为实例仿真模型验证控制器的有效性；文献［17］提出一种控制方式来抑制风电场并网时风电机组产生的次同步振荡问题。

鉴于光伏发电的分布广泛、清洁等优点，基于研究光伏电站并网，提出通过光伏并网设计一种附加次同步阻尼控制器SSDC（SubSynchronous Damping Controller），加在光伏电站主控制器上来抑制交流串补引起的SSR。在保证光伏电站稳定并网的同时，可通过此附加控制器抑制交流串补产生的SSR，很大程度上提高了新能源并网的稳定性与并网效率。只有在严重扰动情况下交流串补才有引发SSR的可能性，且光伏发电具有间断性，故而通过光伏并网附加控制抑制SSR只是作为一种备选方案研究其可行性。

本文以次同步IEEE第一标准模型（IEEE First Benchmark Model）作为实例仿真模型，并建立200×1 MW的光伏电站与之并联接入电网。在PSCAD/EMTDC仿真软件上建立上述电网的仿真模型，仿真结果表明，光伏电站侧的附加控制器可有效快速地抑制交流串补引起的SSR。

1 基本原理

光伏电站并网的拓扑结构图如图1所示。由图1知，IEEE第一标准模型中发电机轴系包括高压缸（HP）、中压缸（IP）、低压缸A（LPA）、低压缸 B（LPB）、发电机（GEN）和励磁机（EXC）6个部分。光伏电站发出直流电汇流后通过逆变站转换为交流电，通过变压器并入交流电网，光伏电站可在汽轮机升压变压器之前或之后并网。其中，RL、XL和XC分别为交流线路电阻、电抗和串补电容；iPV和uPV分别为光伏阵列汇流后的直流电流和电压；CPV为直流侧电容。

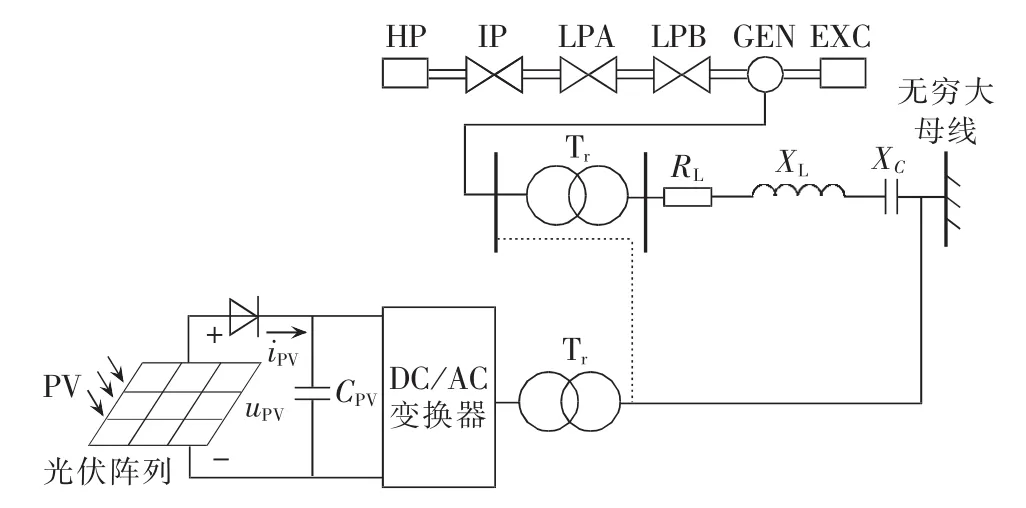
图1 光伏并网拓扑结构图Fig.1 Topology of PV grid-connection

本文研究重点是通过光伏并网控制的研究，来抑制交流串补引起的SSR问题，最大功率跟踪问题不在此做讨论。本文所研究光伏并网时通过电压源换流器 VSC（Voltage Source Converter）逆变联网，会在电网中产生高次谐波，主要由IGBT的开关频率决定，并不会随着附加控制器的加入而变化，且在模型搭建过程中已搭建相应的滤波器，故而没有考虑附加控制对光伏并网的电能质量方面的影响。

1.1 光伏并网控制原理

光伏并网的逆变器采用三相两电平的VSC，其拓扑图如图2所示。其中，Us和Uc分别为电网侧和换流阀侧基频电压分量；Rc和Lc分别为电网侧的等效电阻和电感。

图2 VSC拓扑结构图Fig.2 Topology of VSC

VSC采用脉宽调制PWM（Pulse Width Modulation）技术，并采用应用较为广泛的双闭环解耦控制策略。光伏并网时，有功分量的控制量选择定直流电压控制，为了实现有效抑制SSR的目的，无功分量的控制量为定交流电压控制，控制逻辑图如图3所示。其中，us和uc分别为电网电压和VSC交流侧电压；is为电网电流；L为联结变压器加相电抗器的等效电感；Udc和Uac为直流电压和交流电压；m为调制比；δ为电网侧和换流器阀侧电压的相角差。下标d和q分别表示旋转坐标系下的d轴和q轴分量，上标“*”表示控制量的参考值，无上标表示控制量的测量值。

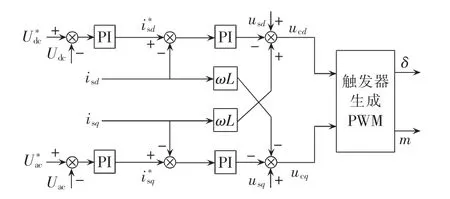
图3 解耦控制逻辑图Fig.3 Logic diagram of decoupling control

VSC的控制量m和δ分别为：

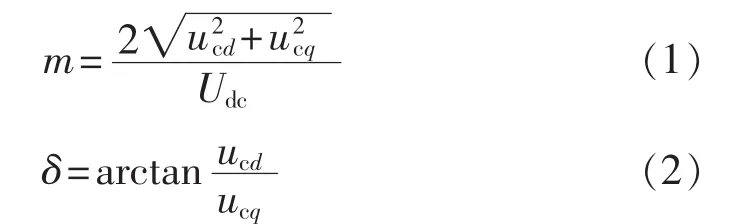
由SSR发生机理知，当电网中的谐振频率与机组轴系自然扭振频率互补时，有可能造成机网耦合彼此互激，故而将设计的次同步阻尼控制器的输出信号加在无功功率控制上，产生的补偿电流通过定转子磁场作用，产生与振荡模态频率一致的电磁转矩分量，进而生成一阻尼转矩分量，实现机组轴系振荡的平稳。SSDC的信号加入图如图4所示。其中，USSR表示阻尼控制器的输出信号。

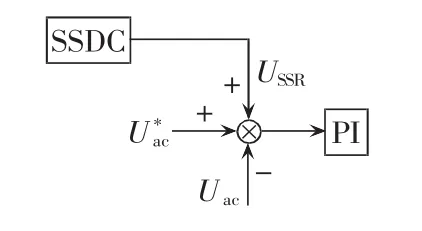
图4 附加SSDC的信号加入图Fig.4 Introduction of SSDC signal

1.2 复转矩系数法

发电机电磁转矩的增量可表示为：

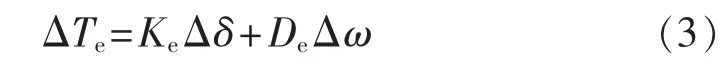
其中，ΔTe为待研发电机的电磁转矩增量；Δδ和Δω分别为该发电机的功角增量和角速度增量；Ke和De分别为同步转矩系数和阻尼转矩系数。ΔTe、Ke、De及Δω均为标幺值；Δδ的单位为rad。

将式（3）进行拉氏变换，可得到电气阻尼系数为：

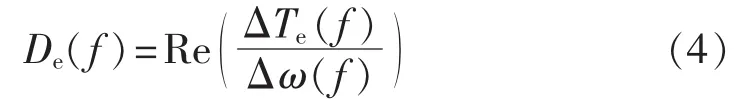
为了达到抑制SSR的目的，需满足De（f）＞0，即需满足发电机转速偏差Δω（f）和电磁转矩偏差ΔTe（f）的相位差介于 0°到 90°之间。

1.3 SSDC设计

为实现次同步阻尼控制能有效抑制SSR，需先测出发电机转速和电磁转矩之间的相位差，然后通过相位补偿达到抑制SSR的目的。

根据复转矩系数法的思想，设计的SSDC结构框图如图5所示。其中，Δω为发电机转速偏差；K为分层控制器的增益。

1.3.1 滤波器设计

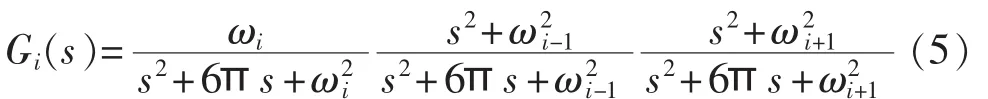
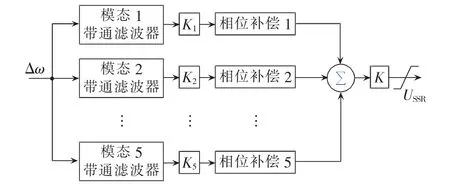
图5 SSDC结构图Fig.5 Structure of SSDC

1.3.2 相位补偿环节

首先得到不同的振荡模态的Δωi和电磁转矩ΔTei的相位偏差，若所需补偿的角度为正，采用超前滞后环节可以实现相位补偿，相位补偿的传递函数为：

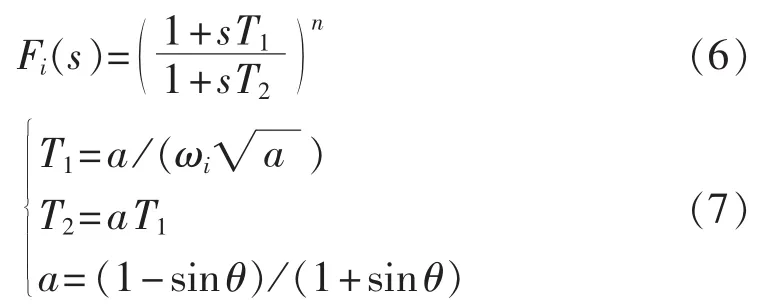
其中，T1和T2为时间常数；θ为待补偿的相位；n为级联的相位补偿环节个数。为了得到较好的相位补偿效果，可以选择多个相位补偿环节级联的形式。

若所需补偿的角度为负，相位补偿的传递函数为：

需要注意的是，在进行相位补偿时，要考虑滤波器的移向作用。

1.3.3 增益环节

当相位补偿角度为正时，经过相位补偿后幅值会发生变化，此时需要调整每个控制模态的增益Ki，以保证每个模态的信号量在相位补偿后幅值的变化不大。

当相位补偿角度为负时，由于式（8）不会对信号的幅值产生影响，故而该移向环节的增益恒为1。

2 算例分析

在PSCAD/EMTDC仿真软件中搭建IEEE第一标准模型与光伏电站并网的结构图，进行仿真。系统拓扑结构图如图1所示，光伏电站接在汽轮机升压变压器的高压侧。

2.1 不加SSDC

2.1.1 时域仿真

在2 s时电网侧施加三相短路故障，故障持续时间为0.075 s。发电机转速信号的仿真结果如图6所示。

我妈扬起手掌，又慢慢放下来，却使力把我拽进她怀里，肥皂的味道混着汗腥味热烘烘地钻进我的鼻子，她的巴掌拍在我背上，声音哽咽着，陈胖子，你还真是个混帐啊。

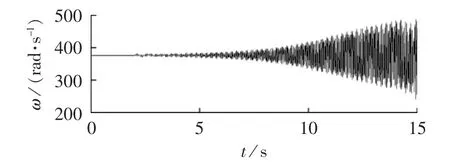
图6 发电机转速Fig.6 Generator speed

由图6知，发电机转速在系统发生扰动后，发生了振荡发散，不利于系统的稳定。各个缸体模块之间的扭振转矩如图7所示。

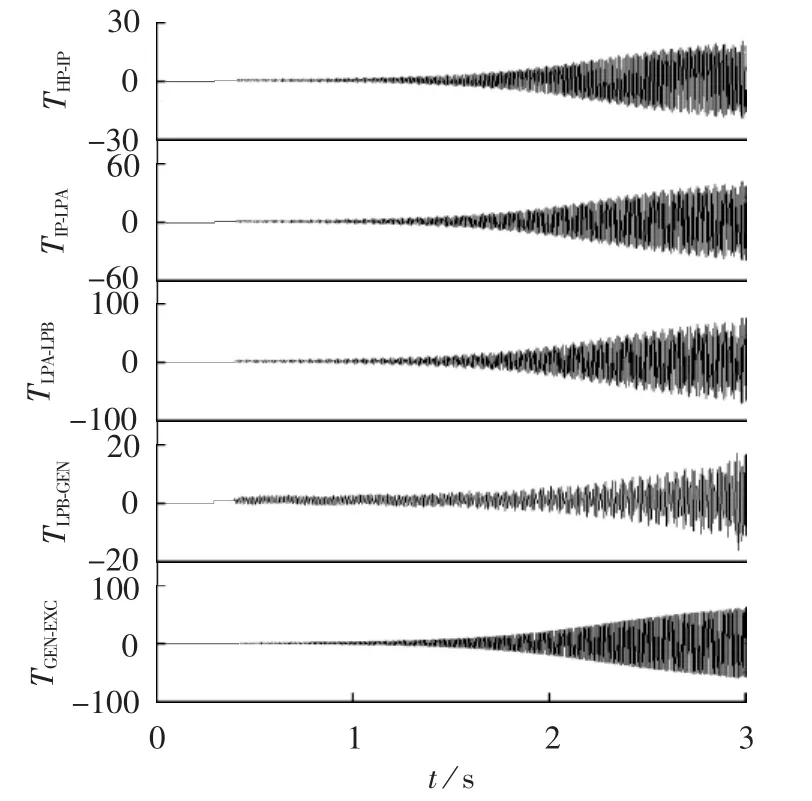
图7 扭振转矩图Fig.7 Torque chart of torsional vibration

由图7知，发电机的6个模块间有5个扭振模式，每个扭振模式都是呈发散状态。在系统发生扰动后，光伏并网输出的有功、无功无功功率如图8所示。

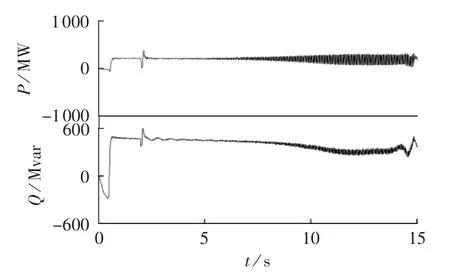
图8 光伏并网的有功、无功功率Fig.8 PV grid-connecting active and reactive powers

由图8知，光伏并网稳定时，向电网输送200MW的有功功率和480 Mvar的无功功率，在系统发生扰动时，有功和无功功率发生波动发散状态，且在13 s后系统呈失稳状态。光伏电站逆变器为VSC，可实现有功无功解耦控制，可实现独立无功发出以维持电压稳定。

2.1.2 特征根分析

取发电机转速信号，采用文献［18］提出的矩阵束算法进行特征根分析，可以得到不同振荡频率下的特征根与相位。光伏并网后SSR模态分析如表1所示。

表1 矩阵束算法辨识结果Table1 Results of identification by MP algorithm

由表1知，光伏并网系统存在5个振荡模态，前4个模态都为负阻尼，第5个模态为弱阻尼，非常容易造成振荡发散，这与时域仿真相一致。辨识出的各个振荡模态的发电机电磁转矩信号相位如表2所示。

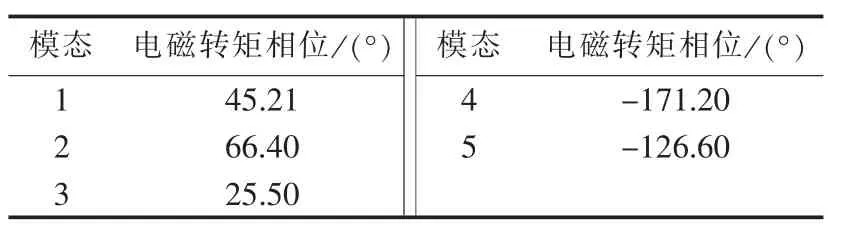
表2 电磁转矩相位Table 2 Phase of electromagnetic torque

2.2 加入SSDC

2.2.1 时域仿真

在加入SSDC前，首先要先得知各振荡模态滤波器的移向角度和Δωi需要补偿的角度。滤波器的移相角和Δωi补偿角如表3所示。

表3 补偿角Table 3 Compensating angle

根据表3列出的补偿相位，分别计算出各振荡模态的相位补偿参数和增益。根据设计的SSDC的输出信号加入到图4所示的位置，加入SSDC以后的发电机转速信号如图9所示。

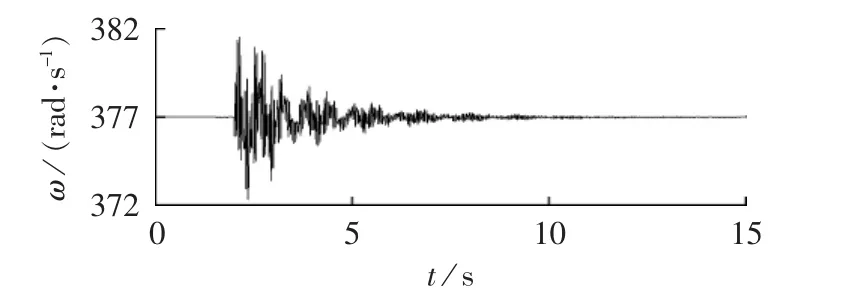
图9 发电机转速Fig.9 Generator speed

由图9知，在系统发生扰动后，发电机转速严重振荡，在SSDC加入后，发电机转速的振荡能迅速平稳下来。加入SSDC后各个缸体模块之间的扭振转矩如图10所示。

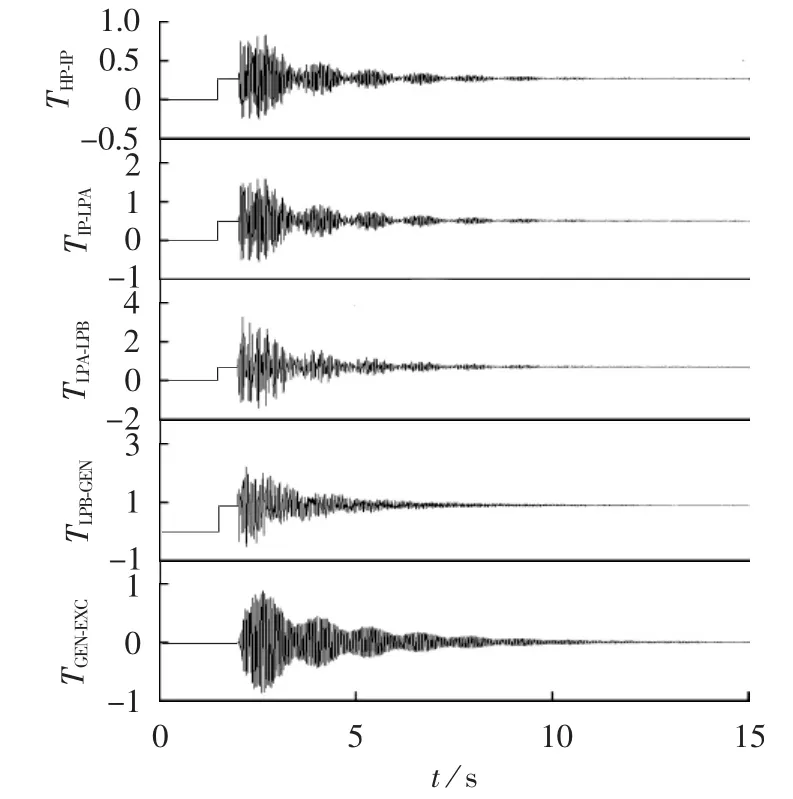
图10 扭振转矩图Fig.10 Torque chart of torsional vibration

由图10知，在加入SSDC以后，发电机各模块之间的扭振转矩可实现快速平稳。光伏并网输出的有功、无功功率如图11所示。

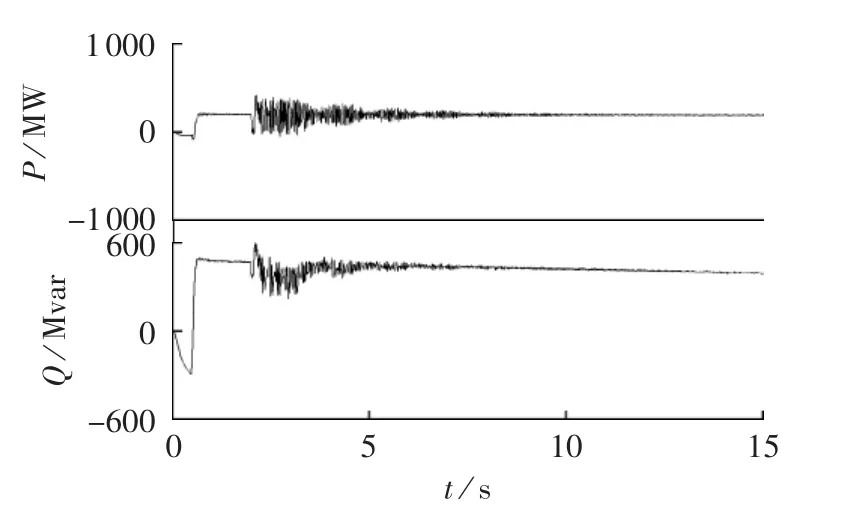
图11 光伏并网的有功、无功功率Fig.11 PV grid-connecting active and reactive powers

由图11知，在SSDC加入时，短时间内加剧了光伏有功、无功功率输出的振荡，但能很快平稳，且振荡不会发散，最终有利于系统稳定。

2.2.2 特征根分析

加入SSDC以后，取发电机转速信号，采用文献［18］提出的矩阵束算法进行特征根分析。分析结果如表4所示。

表4 加入SSDC后矩阵束算法辨识结果Table 4 Results of identification by MP algorithm after SSDC is added

对比表4与表1可知，加入SSDC以后系统在各模态的阻尼比都有很大的提高，且均为正阻尼，系统可以迅速恢复稳定，这与图10的时域仿真结果相一致。

2.3 光伏并网与STATCOM抑制比较

在IEEE第一标准模型交流线路上加入一500 Mvar的STATCOM来抑制SSR，STATCOM的控制方式为定直流电压-交流电压控制策略，然后进行时域仿真。其结果与光伏并网加SSDC的仿真结果相比较，发电机转速的对比图如图12所示。

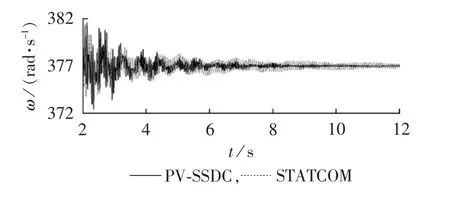
图12 加入SSDC或STATCOM后发电机转速对比图Fig.12 Comparison of generator speed between SSDC and STATCOM

由图12知，当交流输电线路发生故障时，发电机转速的振荡幅值会变大，但加入SSDC以后，发电机转速可以比STATCOM更迅速地抑制SSR，光伏SSDC的抑制效果更明显。在无扰动稳态运行情况下，光伏电站和STATCOM向系统注入的无功分别为480 Mvar和500 Mvar，但STATCOM不向系统注入有功。光伏换流站和STATCOM的无功容量相差不大，故而在扰动时注入的补偿电流幅值相差不大，但光伏并网向系统注入的有功功率会随着电网功率波动而波动，在有功控制环节中PI的作用下，有一定的抑制作用，故而在一定程度上，通过光伏并网抑制SSR的效果要稍好于STATCOM。

依然采用矩阵束算法对通过STATCOM抑制SSR进行特征根分析，分析结果如表5所示。

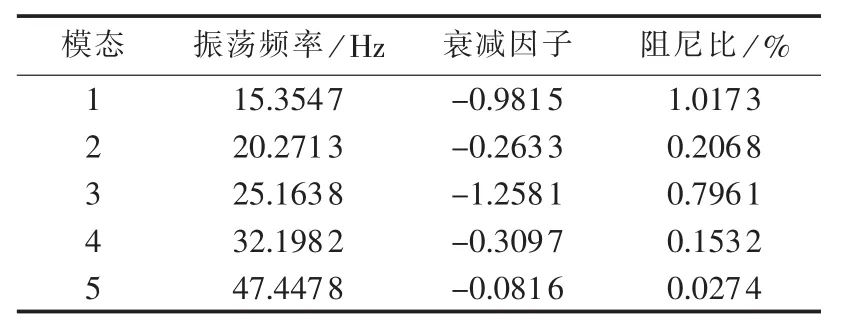
表5 加入STATCOM后矩阵束算法辨识结果Table 5 Results of identification by MP algorithm after STATCOM is added

由表4和表5知，通过光伏SSDC抑制SSR比通过STATCOM抑制SSR产生的阻尼更大，故而抑制效果更明显，这与图12时域仿真结果相一致。

在配置STATCOM参数时，若采用双闭环解耦控制策略，除了配置4个PI控制器参数较为复杂外，还要另设计附加控制器以抑制SSR，对于参数配置跟光伏逆变器的难度相当。但通过在光伏并网附加阻尼控制器，能在保证光伏并网稳定性的同时，不增加一次设备，减小了工程投入，具有很大的经济效益。

3 结论

提出通过光伏电站并网，并在光伏电站的主控制器上加一个SSDC来抑制交流串补引起的SSR，以IEEE第一标准模型作为实例仿真模型，仿真分析结果表明，SSDC加入后可有效抑制SSR。

通过新能源并网抑制SSR，可保证新能源并网稳定性的同时，实现了抑制SSR的目的。控制器的设计只需要取得发电机转速信号即可实现，工程实用性较强，且与STATCOM抑制SSR相比，经济性有很大提高。同时为抑制交流串补SSR问题提供了一种可选方案，鉴于光伏发电具有间断性，在原有的SEDC等控制器因故障未起作用时，通过此后备方法可进一步提高系统稳定性。

［1］CARRASCO J M，FRANQUELO L G，BIALASIEWICZ J T，et al.Power-electronic systems for the grid integration of renewable energysources：a survey［J］.IEEE Transactionson Industrial Electronics，2006，53（4）：1002-1016.

［2］王盼宝，王卫，吴炎.光伏发电系统中无电流传感器型MPPT控制策略［J］.电力自动化设备，2014，34（10）：64-68.WANG Panbao，WANG Wei，WU Yan.Strategy of MPPT control without current sensors for photovoltaic system［J］.Electric Power Automation Equipment，2014，34（10）：64-68.

［3］MUTOH N，OHNO M，INOUE T.A method for MPPT control while searching for parameters corresponding to weather conditions for PV generation systems［J］.IEEE Transactions on Industrial Electronics，2006，53（4）：1055-1065.

［4］李宽，李兴源，陈实，等.光伏并网抑制由直流输电引起的次同步振荡的可行性分析［J］.电力自动化设备，2015，35（3）：41-46.LI Kuan，LI Xingyuan，CHEN Shi，et al.Analysis of damping subsynchronous oscillation caused by HVDC through photovoltaic grid connected［J］.Electric Power Automation Equipment，2015，35（3）：41-46.

［5］KANG B J，LIAW C M.Robust hysteresis current controlled PWM scheme with fixed switching frequency［J］.IEE Proceedings of Electric Power Applications，2001，148（6）：503-512.

［6］PENG Shuangjian，LUO An，CHEN Yandong，et al.Dual-loop power control for single-phase grid-connected converters with LCL filter［J］.Journal of Power Electronics，2011，11（4）：1-8.

［7］LIU B，DUAN S，CAI T.Photovoltaic DC-building-module-based BIPV system-concept and design considerations［J］.IEEE Transactions on Power Electronics，2011，26（5）：1418-1429.

［8］HANG L，LIU S，YAN G，et al.An improved deadbeat scheme with fuzzy controller for the grid-side three-phase PWM Boost rectifier［J］.IEEE Transactions on Power Electronics，2011，26（4）：1184-1191.

［9］KUNDER P.Power system stability and control［M］.北京：中国电力出版社，2001：1025-1071.

［10］DOLAN P S，SMITH J R，MITTELSTADT W A.Prony analysis and modeling of a TCSC under modulation control［C］∥Proceedings of the 4th IEEE Conference on Control Applications.Seattle，USA：IEEE，1995：239-245.

［11］SANCHEZ-GASCA J J，CHOW J H.Performance comparison of three identification methodsforthe analysis ofelectromechanical oscillations［J］.IEEE Transactions on Power Systems，1999，14（3）：995-1002.

［12］ROY R，KAILATH T.ESPRIT：estimation of signal parameters via rotational invariance techniques［J］.IEEE Transactions on Acoustics，Speech，Signal Processing，1989，37（7）：984-995.

［13］PATIL K V，SENTHIL J，JIANG J，et al.Application of STATCOM for damping torsional oscillations in series compensated AC systems［J］.IEEE Transactions on Energy Conversion，1998，13（3）：237-243.

［14］PADIYAR K R，PRABHU N.Design and performance evaluation ofsubsynchronous damping controller with STATCOM ［J］.IEEE Transactions on Power Delivery，2006，21（3）：1398-1405.

［15］BOWLER C E J，BAKER D H，MINCER N A，et al.Operation and testofthe NAVAJO SSR protective equipment ［J］.IEEE Transactions on Power Apparatus and Systems，1978，97（4）：1030-1035.

［16］FARIED S O，UNAL I，RAI D，et al.Utilizing DFIG-based wind farms for damping subsynchronous resonance in nearby turbine-generators［J］.IEEE Transactions on Power Systems，2013，28（1）：452-459.

［17］王波，卢继平，龚建原，等.含双馈机组转子侧附加控制的风电场次同步振荡抑制方法［J］.电网技术，2013，37（9）：2580-2584.WANG Bo，LU Jiping，GONG Jianyuan，etal.A methodto suppress subsynchronous oscillation of wind farm composed of doubly fed induction generators with additionalrotorside control［J］.Power System Technology，2013，37（9）：2580-2584.

［18］CROW M L，SINGH A.The matrix pencil for power system modal extraction［J］.IEEE Transactions on Power Systems，2005，20（1）：501-502.