基于k最短路径算法的负荷停电风险在线评估

王增平，姚玉海，张首魁，郭昆亚

（1.华北电力大学 新能源电力系统国家重点实验室，北京 102206；2.国网辽宁省电力有限公司沈阳供电公司工企自动化，辽宁 沈阳 110811）

0 引言

随着社会对电力依赖程度的不断加深，人们对供电可靠性的要求日益增加。配电网直接面向用户负荷，对供电运行可靠性的影响巨大。因此，在配电系统的范围内，对负荷进行停电的可能性和停电后的严重性进行分析［1］，可以更好地指导事故预防和减少停电带来的损失，对提高供电可靠性具有重要意义。

目前，经过国内外众多专家的不断研究，电力系统风险评估取得了一定成果。文献［2］在风险评估中将风险定义为故障可能性与严重性的乘积，既可以发现低损失高概率的情况，也可以发现高损失低概率的情况，能够为电力系统安全供电提供依据。文献［3］提出一种能灵活响应配电网络拓扑结构变化的复杂放射状配电系统可靠性评估的故障遍历算法。文献［4］将用户作为评估对象，通过对运行中的配电网模拟预想故障下的负荷转移，对运行中配电用户的风险及其紧迫性进行评估，提出了一种面向用户的配电网运行风险评估方法。文献［5］综合考虑不同设备的实时运行状况以及环境状况，采用故障遍历法找出不同设备的故障停电负荷集，计算出不同时点下设备发生故障的实时概率，最终得到不同设备发生故障停电的实时风险值。文献［6］提出一种综合考虑配网重构和紧急切负荷等应急调度措施的灾害下城市配电网停电风险计算方法。文献［7］的基本思路是通过分析各类突发事件造成电力设备停运的概率，计算相应的负荷停电损失和风险，进而给出基于停电风险的应急预警级别。

以上文献的基本思路为：对电网相关设备进行逐一故障假设，采取故障恢复等方法判断是否存在负荷停电情况，再进一步得出相关风险值。这种方法实质上仅体现了假设的故障情况下的风险，结果的准确性受限于模拟故障的规模，并且假设故障之后的故障恢复计算量较大，难以做到在线评估。

针对上述问题，本文提出了一种基于k最短路径算法的负荷停电风险在线评估方法，首先对负荷的停电概率和停电风险进行了定义和阐述，采用k最短路径算法求得负荷的供电路径，再进行安全校验进一步得出负荷的可行供电路径用以计算负荷停电概率，最后通过算例验证了本文方法能够为配电网负荷的应急预警提供辅助决策。

1 停电风险的基本概念

负荷的实时停电风险是指，在时刻t突发事件引发负荷停电的概率和该负荷停电所导致损失的乘积。数学表达式如下：

其中，R（t）为负荷在时刻 t的停电风险值；φ（t）为负荷在时刻t的停电概率；S为负荷停电所导致的损失。

1.1 损失的确定

负荷停电所导致的损失采用该负荷在时刻t的有功功率和负荷的相对重要程度来表征，数学表达式如下：

其中，p为用户数；Pi（t）为时刻 t用户 i的有功功率；ci为用户i的相对重要程度。

1.2 负荷停电概率的确定

我国配电网呈环形设计，开环运行。各条配电线路以常开的联络开关保持着“手拉手”的供电模式，若发生故障，通过开关操作将非故障失电区域负荷转移到其他供电路径，以提高供电可靠性。所以，负荷的停电概率是由所有可行的供电路径（这些供电路径可能来自相同或不同电源点）中的设备故障率决定的。进一步地，负荷的在线停电率由这些设备在当前时刻的故障率决定。

目前，在设备实时故障率［7-9］的研究上已取得一定成果，这些方法可以综合考虑历史及未来的天气状况、环境温度、风速、风向、日照热量、负荷水平、服役时间等条件对变压器和输电线路短期可靠性的影响，有效反映当前时刻的设备故障概率。在计算设备实时故障率时，本文采用文献［9］所述方法。

在所有可行供电路径的设备故障率得出的基础上，负荷的停电率再根据供电路径的连接关系进一步得出。连接负荷和电源的供电路径分为2种情况。

（1）仅存在1条供电路径。当只存在1条供电路径时，由于配电网的放射状运行，负荷与电源点之间的设备只会出现串联关系，即负荷的停电率为串联设备故障率的和。如图1所示，节点1为电源点，负荷的停电率为 φ（t）12+φ（t）23。

图1 单一供电路径示意图Fig.1 Schematic diagram of single power-supply path

（2）存在多条供电路径。当负荷与电源之间存在多条供电路径时，负荷停电概率取决于不同供电路径停电率和这些供电路径中是否存在公共路径（即不同供电路径中含有相同设备）。其中，供电路径停电率为该路径上所有设备停电率的和。

根据是否存在公共路径可分为2种情况。

a.若不同供电路径之间不存在公共路径，则负荷的停电率为供电路径停电率的并联，即为供电路径停电率的乘积。以图2（a）为例，节点1和3为电源点，负荷共有2条可行的供电路径（1-2和3-2），则负荷的停电率为这2条供电路径停电率的乘积，即 φ（t）12φ（t）23。

b.若不同供电路径之间存在公共路径，则负荷的停电率要根据实际设备的串并联关系来确定，设备串联则为相应设备故障率的和，设备并联则为相应设备故障率的积。以图2（b）为例，节点1和4为电源点，负荷共有2条可行的供电路径（1-2-3和4-2-3），则负荷的停电率为 φ（t）12φ（t）24+φ（t）23。

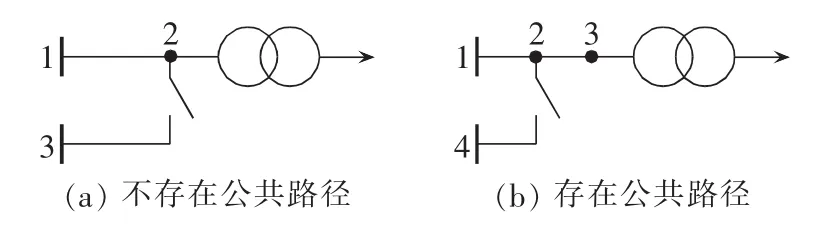
图2 多条供电路径示意图Fig.2 Schematic diagrams of multiple power-supply paths

从以上分析可知，负荷的停电概率是由所有可行的供电路径中的设备故障率决定的。然而实际配电网结构复杂，负荷与电源点间的可行供电路径往往并不唯一。在电网结构复杂和负载率较低的情况下，部分负荷的可行供电路径数目可能会较多，在短时间内难以全部得出。其实，即使全部得出，实际意义也不大，因为负荷上游电气设备故障导致停电时，故障恢复时实际仅需1条供电路径来转供该负荷。所以，根据实际情况选取具有代表性的k条可行供电路径来计算负荷的停电概率就可以满足工程实际需要，其中k为路径的个数。根据路径停电率由低到高的顺序依次得到负荷对应的k条可行供电路径，这样进一步计算出的负荷停电概率之间具有可比性，也能很好地体现出负荷停电可能性。

2 k最短路径算法

k最短路径的求取是图论中的一个基本问题，旨在寻找源点和终点之间所有可达路径中最短、次短，直到第 k短的路径［10-13］。 本文采用文献［13］所述k最短路径算法来求取可行供电路径，该算法有效利用了已经得到的前k-1条短路径的信息，算法原理简单，计算效率高。但该算法没有对环路进行限定，即在求取k最短路径时，可能会出现含有环路的路径，这不符合配电网的实际运行情况。针对配电网的放射状运行特点，在算法过程中进行了环路检验，采用改进后的算法可按照路径距离由小到大的顺序依次求出，得出的路径中不含有环路，符合实际工程需求。

2.1 拓扑描述

在建立拓扑联系时，将负荷点和电源点视为节点，连接节点之间的设备为支路，支路的距离为该支路上设备所对应的故障率。

建立电网的邻接矩阵A，邻接矩阵元素aij的赋值分为3种情况：

（1）i=j时，则 aij=0；

（2）i≠j且节点 i与节点 j之间无支路，则 aij=∞；

（3）i≠j且节点i与节点j之间有支路，则 aij=φ（t）ij。

2.2 k最短路径算法步骤

k最短路径算法步骤如下。

（1）输入基本电气信息，电网含有M个电源节点、N个负荷节点，建立电网的邻接矩阵A。设置需要求得的路径个数k，其中k为负荷点到一个电源点的路径个数。路径个数k的设置需要根据实际电网的复杂程度来确定，一般情况下，将k设置为2或3就可满足工程实际。

初始化m=1，建立APaths矩阵用以存放最短路径、次短路径，直到k最短路径。建立ADists矩阵存放所有负荷节点到源点的最短距离。用APathdists存放最短路径距离、次短路径距离，直到k最短路径距离。建立ANeighbors矩阵存放APaths矩阵里路径对应的邻近点。邻近点为与路径上除源点外的所有节点有直接连接关系的节点。如图3所示，路径12-9-8-2的邻近点为 10和 11。

图3 IEEE 3馈线配电系统图Fig.3 IEEE 3-feeder system

（2）本文采用 Dijkstra 算法［14］求出所有负荷节点到电源点m的最短路径，且所有负荷节点到电源点m的最短路径分别存入APaths和Apaths矩阵中，短路径对应的距离存入 ADists、APathdists、Adists和 Apathdists中，并设置λ=1、τ=1。 其中，Apaths、Adists和 Apathdists与 APaths、ADists和APathdists功能相同，用以算法过程中的中间存储。

（3）求出 Apaths里存放路径的邻近点，并存入ANeighbors中。

（4）计算经过τ次短路径经邻近点vt的路径vm-vt-vi-vj的距离，并存入ATempdists中。 其中，vi为邻近点t相邻的τ次短路径上的节点；vm-vt为源点m到节点t的最短路径；vt-vi为节点t与节点i的支路；vi-vj为τ次短路径节点i到终点j的路径。

（5）将ATempdists中距离最小的路径存入Apaths中，并且τ=τ+1。再判断该路径是否含有环路，判断的方法是检查路径中是否含有相同的节点，若不含有相同的节点则说明该路径中不含有环路，则将该路径存入APaths中，并且λ=λ+1。若含有相同的节点则进行下一步。

（6）判断Apaths里存放的路径是否还有邻近点，若没有邻近点则进行下一步。若含有邻近点则进一步判断λ是否等于k，若等于则进行下一步，否则转步骤（3）。

（7）判断算法结束条件，若m＞M，则算法结束，否则m=m+1并转步骤（2）。

3 路径的安全运行校验

将负荷的供电路径求出后还需要进行安全校验，通过潮流计算来验证这些路径是否满足电网运行的安全约束，并将不满足安全约束的供电路径删除。

配电网运行需要满足的安全约束为［15］：

（1）配电网络的拓扑约束，配电网拓扑结构为放射状的连通网络；

（2）配电网络的节点电压约束；

（3）配电网络的支路电流约束；

（4）变电站主变的容量约束。

路径安全校验是在电网当前运行方式下，将路径连接于与该路径电源所在的馈线，再视情况进行潮流计算来验证是否符合安全约束。为了节省计算资源，将路径分为2种情况。

a.路径不属于该路径电源所在馈线。这种情况需要将路径连接于其供电馈线，再仅对该馈线进行潮流计算来验证安全约束。由于本文只关心该负荷有关的馈线运行情况，电网的其他部分则不需要进行安全校验。

b.路径属于该路径电源所在馈线。由于该负荷本身由该电源供电，符合电网安全约束，所以不需要进行潮流计算来验证安全约束。

以图3所示电网为例，在当前运行状态下，负荷节点9到电源节点3的路径为9-8-10-14-13-3，该路径与电源3所在馈线进行合并后的馈线如图4（a）所示，再仅对该馈线进行潮流验证。负荷节点15到电源节点3的路径为15-13-3，该路径属于电源点3所在馈线，如图4（b）所示，则不需要潮流计算。

图4 合并后的电网图Fig.4 Distribution network after merging

4 负荷停电风险在线评估的步骤

负荷停电风险在线评估的步骤如下：

（1）计算出电网设备故障率；

（2）得出各个负荷节点的k最短路径；

（3）对各个负荷节点的路径进行安全校验，删除不满足安全约束的供电路径；

（4）根据设备故障率和负荷可行供电路径得出各个负荷的停电率；

（5）根据负荷停电概率、有功功率和重要程度计算出负荷的风险值。

5 算例分析

算例1：为了说明本文方法的有效性，采用文献［7］所述IEEE 43节点算例进行对比验证。IEEE 43节点系统如图5所示，该系统共有15处负荷（图中连有箭头的节点），节点1为系统唯一电源节点。虚线框所在区域为受灾区域，线路停运概率、负荷量、负荷重要等级、经济价值系数参见文献［7］。由于该算例没有描述联络开关及重构信息，设置k=1。

表1列出了本文方法和文献［7］得到的负荷停电概率和风险值。从表1所列结果可以看出，根据停电概率由高到低的顺序，本文方法得出了与文献［7］相同的结果，均为节点 36、38、42、24，在一定程度上说明了本文方法的有效性。根据风险值由高到低的顺序，本文方法的结果为节点 38、42、24、36；文献［7］的结果为节点 42、38、24、36。 节点 38 负荷量较大，停电概率较高，并且相对位于系统的上游，本文方法得出节点38风险最高更具有合理性。

图5 IEEE 43节点系统图Fig.5 IEEE 43-bus system

表1 负荷停电概率和停电风险Table 1 Power outage probability and risk

算例2：为了进一步说明本文方法的优越性，采用如图3所示的3馈线配电系统为例，该电网额定电压为23 kV，基准容量为100 MV·A，总负荷为28.7+j 17.3 MV·A，共有16个节点、16条支路，本文假设16条支路均装设开关设备，图中实线和虚线分别表示处于闭合和断开状态，节点负荷和电容器容量参考文献［16］。时刻t电网运行方式如图3所示，计算得出网络总损耗为511.44 kW，3条馈线出线电流为：1-4（394.13 A）、2-8（691.61 A）、3-13（223.53 A）。假设16条支路的额定电流为750 A，16个节点负荷的重要性相同，并令相对重要程度c=1，设置k=2。假设时刻t的设备故障率如表2所示。

表2 设备故障率Table 2 Equipment failure rate

表3列出了分别采用本文方法和文献［7］所述方法（故障恢复采用文献［15］所述方法）得到的负荷停电概率和风险值。

表3 负荷停电概率和停电风险Table 3 Power outage probability and risk

采用本文方法得出节点12的停电概率最高，节点8的停电概率最低；节点12的风险值最高，节点8的风险值最低。采用文献［7］所述方法得出节点12的停电概率最高，同时该节点风险值也最高，而其他大部分节点没有停电概率和风险。

为了说明本文方法，以节点4为例。采用k最短路径方法得出节点4到电源点1的最短供电路径为1-4，无次短路径。节点4到电源点2的最短供电路径为2-8-9-11-5-4，次短路径为2-8-10-14-13-15-16-7-6-4。节点4到电源点3的最短供电路径为3-13-14-10-8-9-11-5-4，次短路径为3-13-15-16-7-6-4。经过安全校验之后，路径1-4、3-13-15-16-7-6-4为可行供电路径，这2条供电路径并无公共路径，路径停电率分别为0.0015和0.2522，则负荷的停电概率为0.0004。

采用文献［7］所述方法仅负荷5和12有停电概率和风险值，而其余节点没有停电风险。得到这个结果的原因是文献［7］首先假设负荷不停电的概率为1，然后依次选取设备进行故障假设，然后对非故障失电区域负荷进行故障恢复或孤岛划分，进而判断设备故障后是否会引起负荷停电。若存在停电负荷则更新对应负荷的停电概率，否则不更新。在图3所示配电网中，对16条支路进行逐一故障假设，仅负荷5和12会出现无法转供的情况，而其他负荷在任一故障假设下均可被转供。

文献［9］实质上属于一种确定性的安全评估，在电网当前运行状态下，仅考虑了负荷实际供电路径上的设备故障率的影响，无法计及转供路径上设备的故障率及其影响。本文方法考虑了负荷所有可行供电路径的设备故障率的影响，可以更好地体现配电网运行中的不确定性因素，得到的停电率和风险值更能体现负荷在当前时刻的风险情况。

本文方法与文献［9］所得计算所需时间分别为7.66 s、46.53 s，可以看出，本文方法的计算时间明显小于文献［9］，这是因为本文方法不需要进行复杂的故障恢复或孤岛划分计算，有效地节省了计算时间，可以更好地满足在线计算的要求。

6 结论

本文采用k最短路径算法求解负荷在线停电风险评估，得出以下结论：

（1）本文方法定义的负荷停电概率和停电风险充分考虑了电网的拓扑结构的影响，得到的负荷停电概率和停电风险更加准确；

（2）负荷停电概率和停电风险不仅计及当前供电路径设备的故障率，还计及了转供路径设备的故障率，得到的停电概率和停电风险更能体现负荷的实际风险；

（3）采用的k最短路径算法原理简单，易于编程实现，避免了设备故障枚举之后的故障恢复或孤岛划分计算，节约了计算资源，可以满足在线评估的需求。

［1］范云滩，刘剑，李俊娥，等.基于符号动力学的配电网结构风险评估［J］. 电网技术，2013，37（5）：1244-1251.FAN Yuntan，LIU Jian，LI Jun’e，et al.Symbolic dynamics based risk assessment of distribution network structure［J］.Power System Technology，2013，37（5）：1244-1251.

［2］CIGER Task Force 38.03.12.Power system security assessment：a position paper［J］.Electra，1997（175）：49-77.

［3］李志民，李卫星，刘迎春.复杂辐射状配电系统可靠性评估的故障遍历算法［J］. 电力系统自动化，2002，26（2）：53-56.LI Zhimin，LI Weixing，LIU Yingchun.Fault-traversal algorithm of complex radial distribution-system-reliability evaluation［J］.Automation of Electric Power Systems，2002，26（2）：53-56.

［4］刘健，韩磊，张志华.面向用户并考虑紧迫性的配电网运行风险评估［J］. 电力自动化设备，2015，35（2）：19-23.LIU Jian，HAN Lei，ZHANG Zhihua.Customer-oriented distribution network operationalrisk assessmentconsidering urgency ［J］.Electric Power Automation Equipment，2015，35（2）：19-23.

［5］赵会茹，李娜娜，郭森，等.配电网设备故障停电风险实时评估［J］. 电力自动化设备，2014，34（11）：89-94.ZHAO Huiru，LI Nana，GUO Sen，et al.Real-time risk assessment on equipment failure outage of distribution network［J］.Electric Power Automation Equipment，2014，34（11）：89-94.

［6］俞隽亚，王增平，田红雨，等.基于最小过热区域的城市配电网灾害风险评估［J］. 电力系统保护与控制，2015，43（4）：115-120.YU Junya，WANG Zengping，TIAN Hongyu，et al.Risk assessment of urban distribution network under disaster based on minimum over-heated region［J］.Power System Protection and Control，2015，43（4）：115-120.

［7］李锐，陈颖，梅生伟，等.基于停电风险评估的城市配电网应急预警方法［J］. 电力系统自动化，2010，34（16）：19-23.LIRui，CHEN Ying，MEIShengwei，etal.An earlywarning method for emergency response based on power failure risk analysis of distribution systems［J］.Automation of Electric Power Systems，2010，34（16）：19-23.

［8］刘海涛，程林，孙元章，等.基于实时运行条件的元件停运因素分析与停运率建模［J］.电力系统自动化，2007，31（17）：6-11.LIU Haitao，CHENG Lin，SUN Yuanzhang，et al.Outage factors analysis and outage rate model of components based on operating conditions［J］.Automation of Electric Power Systems，2007，31（17）：6-11.

［9］何剑，程林，孙元章，等.条件相依的输变电设备短期可靠性模型［J］. 中国电机工程学报，2009，29（7）：39-46.HE Jian，CHENG Lin，SUN Yuanzhang，et al.Condition dependent short-term reliability models of transmission equipment［J］.Proceedings of the CSEE，2009，29（7）：39-46.

［10］MATTHEW W，CARLYLE R，KEVIN W.Near shortest and kshortest simple paths［J］.Networks，2005，46（2）：98-109.

［11］PALUCH S.A multipliable algorithm fork shortestpaths problem［J］.Komunikacie，2009，11（3）：11-14.

［12］戴树贵，陈文兰.一个求解k短路径实用算法［J］.计算机工程与应用，2005，41（36）：63-65.DAI Shugui，CHEN Wenlan.A practical algorithm for the k shortest-path problem［J］.Computer Engineering and Applications，2005，41（36）：63-65.

［13］白轶多，胡鹏，夏兰芳，等.关于k次短路径问题的分析与求解［J］. 武汉大学学报信息科学版，2009，34（4）：492-494.BAI Yiduo，HU Peng，XIA Lanfang，et al.A kth-shortest path algorithm based on k-1 shortest paths［J］.Geomatics and Information Science of Wuhan University，2009，34（4）：492-494.

［14］乐阳，龚健雅.Dijkstra最短路径算法的一种高效率实现［J］.武汉测绘科技大学学报，1999，24（3）：209-212.YUE Yang，GONG Jianya.An efficient implementation of shortest path algorithm based on Dijkstra algorithm［J］.Journal of Wuhan Technical University of Surveying and Mapping，1999，24（3）：

（continued on page 23）（continued from page 5）209-212.

［15］徐玉琴，张丽，王增平，等.基于多智能体遗传算法并考虑分布式电源的配电网大面积断电供电恢复算法［J］.电工技术学报，2010，25（4）：135-141.XU Yuqin，ZHANG Li，WANG Zengping，et al.Algorithm of service restoration for large area blackoutin distribution network with distributed generators［J］.Transactions of China Electrotechnical Society，2010，25（4）：135-141.

［16］CIVANLAR S，GRAINGER J J，YIN H，et al.Distribution feeder reconfiguration for loss reduction［J］.IEEE Transactions on Power Delivery，1988，3（3）：1217-1223.