直流接地极极址勘测的研究

徐碧川，鲁海亮，潘卓洪，文习山，蓝 磊，李 伟

（武汉大学 电气工程学院，湖北 武汉 430072）

0 引言

随着我国经济的高速发展，直流输电在我国取得了迅速的发展［1-3］。直流接地极在直流输电中起到正常运行时箝制中性点电位和单极大地运行时泄放入地电流的重要作用，在直流输电工程规划初期，须进行直流接地极的设计以及极址的选取工作［4］。

由于交流系统的跨度以及低阻特性，直流输电入地电流会引起交流电网变压器直流偏磁［5］，对电力系统的安全运行造成严重危害［6-9］。目前，变压器的直流偏磁问题已成为直流输电领域研究的重要问题。由于直流输电受端换流站往往处于经济发达区域，交流网络庞大复杂，并且由于勘测以及征地问题，直流接地极极址无法远离高压变电站，使得交流电网内直流偏磁危害尤其突出。

直流接地极极址的勘测涉及到接地极自身的安全性能及其对交流电网和其他系统的影响评估。选址初期，需要对待选极址土壤进行勘测，目前学者研究的主要土壤模型为水平和垂直层状模型［10-11］、复合结构模型［12-14］。长距离直流输电的入地电流具有很强的穿透能力，文献［15］指出，约有30%的电流可以穿透到深度为直流极距离的大地中；文献［16-17］得出了深层土壤电阻率对于地表电位的分布有着重要影响的结论。可见，接地极极址勘测时的测深与测量范围对于准确建立土壤模型以及评估［18］接地极对其他系统的影响具有重要作用。

在电力系统中，广泛使用传统的四极法作为大地电阻率的测量手段，但对于研究直流接地极对环境以及其他系统的影响时，应该考虑大深度范围的大地电阻率的测量，需要使用地质勘探领域的大地电磁 MT（MagnetoTelluric）［19］法进行。 由于土壤分布的不均匀性，各测点通过MT法勘测得到的数据可能存在较大差异。在运用MT法进行直流接地极选址时，MT法的测量范围以及测深没有规程可以参考，对于MT法的测量结果的评价也没有参考依据。

本文将从地表电位分布以及直流偏磁计算的角度，针对直流极选址时土壤的勘测范围、测深提出参考标准，并针对土壤勘探的测量结果提出评价的标准，同时在勘探方案上提出相应建议。

1 直流接地极选址的理论模型

研究直流接地极极址土壤勘探的范围、勘探结果的评价标准以及确定直流接地极优化选址时，主要涉及：水平多层土壤地表电位分布模型、大地回流理论模型、交流电网直流电流分布的计算模型这3个模型。

1.1 水平多层土壤地表电位分布模型

在研究直流电流从直流极注入时，一般考虑将接地极细分为足够稠密的导体段，运用场路结合的节点电压法来计算地表电位的分布［20］。在计算与直流接地极距离大于接地极尺寸10倍的地表电位时，接地极的形状对地表电位的影响很小，此时可以将接地极等效为一个点电流源来研究［21］。

在如图1所示的多层水平土壤的分层模型下，导电媒质中单位点电流源所产生的电位表达式被称为格林函数。对于点电流源在第m层、场点在第i层的格林函数的表达式［17］为：

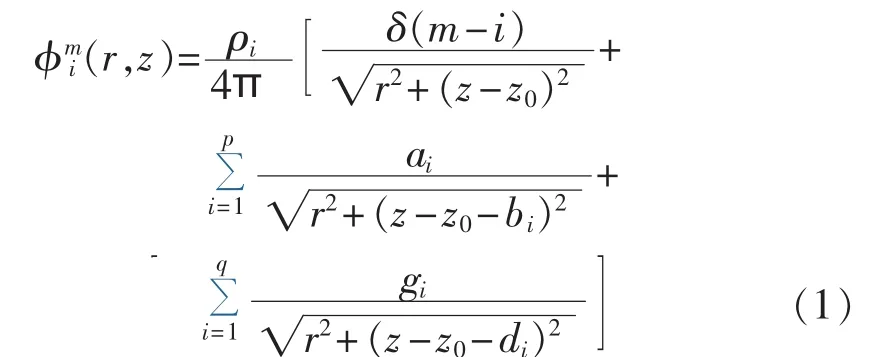
其中，ρi为第i层土壤的电阻率；z0为源点的深度；z和 r为极坐标的 2 个维度；ai、bi、gi、di为通过复镜像法求解得到的系数；p、q分别为2组复镜像系数的个数；δ为狄利克雷函数。

由于本文研究的土壤模型存在明显的奇异性，ai、bi、gi、di可以通过文献［16］介绍的高阶复镜像法进行求解。

图1 土壤水平分层模型Fig.1 Horizontal layer model of soil

1.2 大地回流理论模型

通过1.1节得到的电位函数进行求偏导，可以求得土壤中任一点的电场强度和电流密度，通过对电流密度的积分可以得到任意深度范围内流过的电流大小。

对电位函数求水平方向的偏导，得到水平方向的场强函数：

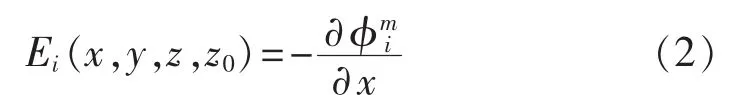
该点水平方向的电流密度为：

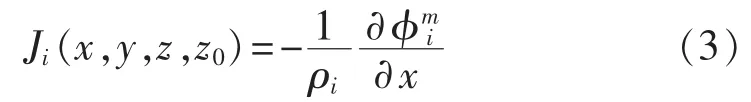
通过第i层土壤纵向截面的电流大小为：

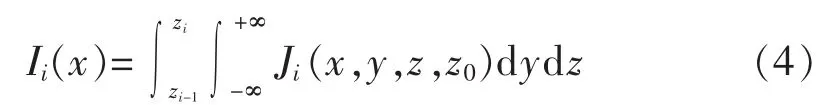
联立式（2）—（4）可以得到：

其中，Pi和Qi分别为第i层土壤对应的2组复镜像系数的个数。

根据式（5）可以计算单极大地运行情况，直流入地电流在距离直流极不同距离的剖面上任意深度范围内流过的电流占总入地电流的百分数。

1.3 交流电网直流电流分布的计算模型

对于任意参数在交流电网直流网络参数确定的情况，使用节点电压法有：

其中，G为节点电导矩阵；V和I分别为节点电压和注入电流列向量。在I中取出非零分量J，即变电站接地中性点注入列向量，由变电站中性点的戴维南等效有：

其中，H为接地中性点与所有节点间的关联矩阵；K为非接地中性点的关联矩阵；R、J和V分别为变电站的接地电阻、接地中性点注入电流和地表电位列向量；I1为变电站入地电流列向量。由变电站地表感应电位的定义有：

其中，M1为变电站间互阻；M0为变电站与直流极间互阻，可由1.1节中介绍的方法求解；I0为直流极的入地电流列向量。由式（7）—（11），可以计算直流工程单极大地运行时交流电网中直流电流的分布。

2 直流接地极选址时的土壤勘探

直流接地极在选址时，除了需要考虑接地极的跨步电势、发热问题，还需考虑直流接地极对周围环境的影响。规程［4］规定，需对预选极址20 km范围内的地质、水文情况进行调查勘测，且在预选极址10 km范围内原则上不宜有地下金属管道、铁道以及有效接地的变压器。

2.1 极址土壤勘测范围推荐值

根据如图2所示的典型大地的结构，最上层为腐殖土层，其电阻率在10～1000 Ω·m之间，厚度为几米到几十米；第2层为全新世地层，其电阻率在 100～400 Ω·m 之间，厚度为 1～4 km；第 3 层为原始岩石，其电阻率在1000～20000 Ω·m之间，厚度为10～30 km；第4层为层地球的内部热层，土壤电阻率很小，厚度认为很大。选取典型土壤结构参数见表1。

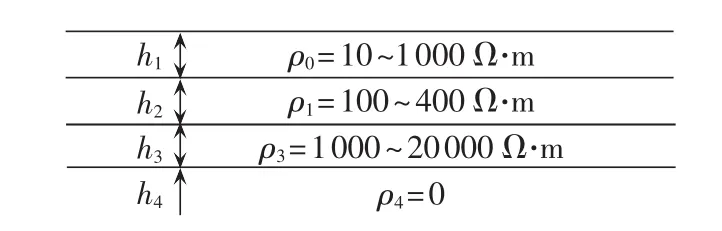
图2 典型大地分层结构Fig.2 Typical layered structure of earth

运用大地回流理论可以求得直流输电工程单极大地运行时，距离直流接地极不同距离的土壤垂直剖面上各深度范围内直流电流分布的百分数。如果某深度以下流过的电流占总入地电流的60%，则定义该深度为60%入地电流透深。假设直流输电工程双极相距1000 km，两直流极埋深均为3 m。根据在我国青海格尔木、湖北宜昌、广东惠州三地运用MT法对大地电阻率测量所得的实测值，以及经典大地分层结构，分别计算4种土壤结构下与直流接地极不同距离的60%入地电流透深，计算结果见图3。

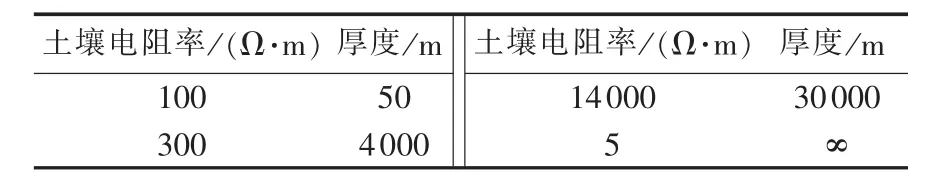
表1 大地典型分层模型参数Table 1 Parameters of typical earth layer model

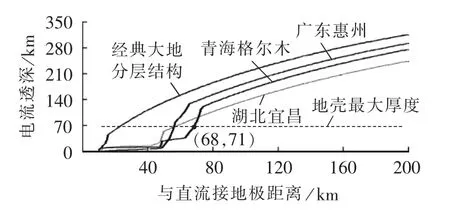
图3 4种土壤结构下60%电流透深曲线Fig.3 60%current penetrating depth curve for four kinds of soil structure

从图3中可以得到，随着与直流接地极距离的增加，直流入地电流趋于流向数百千米以下深度的深层土壤，因此，在进行直流接地极选址时，深层土壤的结构是不可忽略的。

我国地壳厚度最大的地区为青藏高原，最大厚度达70 km，如果60%入地电流透深达到70 km的地壳，大部分电流透过地壳从地幔中流过，则此时可以认为大部分电流已流入底层土壤。

在直流接地极选址时，通常用MT法测量大地结构，规程［4］中推荐测量待选极址周围20 km范围内的地质结构，从图3中可以看出，在经典大地分层结构下，60%入地电流透深达到距地表70 km深的地幔层时，与直流接地极距离约为20 km，与规程结论相符。我国青海格尔木、湖北宜昌、广东惠州三地可以分别代表我国高海拔地区、中部平原地区以及低海拔沿海地区的土壤结构。根据图3结果，在格尔木土壤结构下，60%入地电流透深达到地幔层时，与直流接地极的距离约为70 km，此时大部分电流从地幔中流过，浅层土壤中流过的电流很小，因此，超过此范围外可不关心浅层土壤的结构。如果认为在直流接地极对电网影响范围内的深层地幔土壤结构具有一致性，则在此范围以内测量表层至深层土壤结构具有较大参考价值。因此，在进行直流接地极选址时，本文推荐使用MT法测量待选极址周围70 km范围内表层到深层土壤的大地电阻率。

2.2 极址土壤勘测深度推荐值

由于各地区土壤结构差异巨大，研究接地极极址土壤的勘探深度问题时比较困难。由图3可以得到，在经典大地分层结构下，电流的穿透深度高于其他3种土壤结构，考虑最保守的情况，本文选用经典大地分层结构来研究选址时土壤的勘探深度。

MT法对土壤的探测深度与探头的探测频段有关，探头频段的下限值越小，则其探测深度越大。根据经典大地分层结构，大地结构中存在原始岩石层，电阻率很高，其电阻率在1000～20000 Ω·m之间，厚度在10～30 km之间；其下存在内部热层，土壤电阻率很小，厚度很大。

本文从直流偏磁计算的角度，研究MT法测深不够对交流电网直流偏磁计算的影响。规程［4］规定在距离直流接地极10 km以内不允许存在接地变压器，假设交流电网分布在距离直流极10 km以外的范围，交流线路的直流电阻为 0.03 Ω/km，线路长度大于 20 km，接地变压器接地电阻为0.2 Ω，接地变压器绕组的每相直流电阻为0.3 Ω。

为了研究底层土壤对直流偏磁计算的影响，通过改变底层土壤的电阻率，可以得到地表电位分布的差异曲线。由于电网的结构未知，本文使用贪婪算法，根据地表电位分布的差异曲线，对可能位于不同位置的2座变电站及其之间的线路的直流电流大小进行计算，可以得到土壤结构参数的差别对于变压器中性点电流计算的影响，如图4所示。图中，ΔU1、ΔU2分别为底层土壤的改变对两站地表电位造成的差异；ΔI为电位差异造成的中性点电流的差异。改变底层土壤电阻率，得到最大中性点电流差异ΔImax如表2所示。

如果把限定的中性点电流的最大差值设定为1 A，则底层土壤电阻率的可变范围是（0，1320）Ω·m，临界土壤反射系数为-0.827，超出此范围则认为会对中性点电流的计算造成较大影响。从表2可知，如果测深不能穿透高阻层，而把底层也当作高阻层，则会对中性点电流的计算值造成巨大影响，所以对极址土壤进行勘测时，必须使测量深度穿透高阻层。

图4 地表电位的差异造成的中性点电流计算误差Fig.4 Neutral current calculation error due to ground potential difference

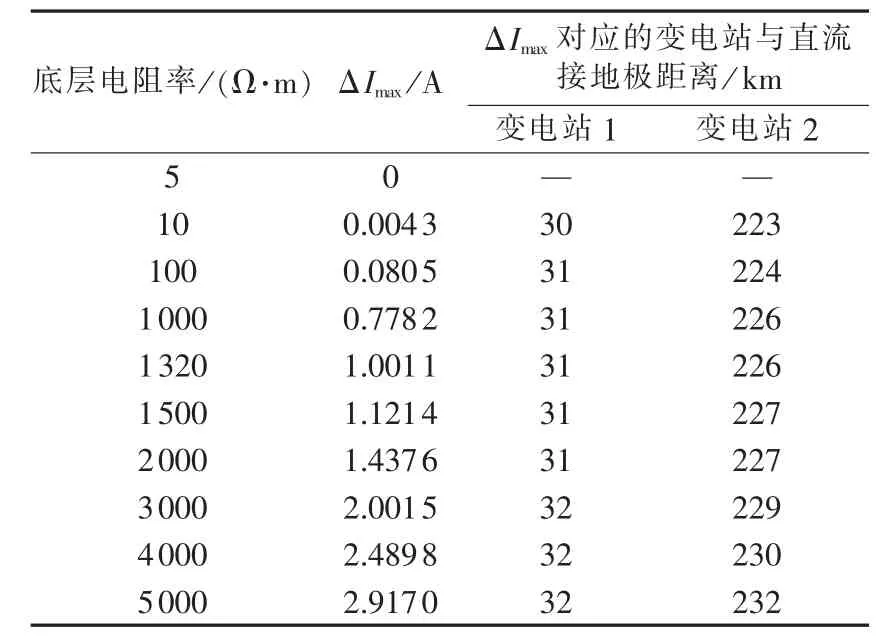
表2 不同的底层电阻率对应的中性点电流计算误差Table 2 Neutral current calculation error for different bottom layer resistivities

在经典土壤参数的范围内，通过改变表1中高阻层的厚度以及电阻率，以中性点电流的最大误差值1 A作为限定条件，计算底层土壤的临界土壤电阻率和反射系数，结果见表3。

表3 临界土壤电阻率和反射系数计算Table 3 Calculation of critical soil resistivity and reflection coefficient

从表3中可以得出3个结论：

a.高阻层厚度越大，对下层土壤的屏蔽作用越大，则下层土壤电阻率的可变范围越大，临界反射系数的绝对值越小；

b.高阻层电阻率越大，则临界反射系数的绝对值越大，底层土壤电阻率的可变范围越大；

c.根据以上2个结论可以得出，如果在测深穿越高阻层且电阻率逐渐降低时，只要最终测深对应的电阻率小于对应的临界电阻率，则该深度以下的土壤电阻率对中性点电流的计算偏差可以控制在限定范围以内。

运用MT法对土壤电阻率进行实际测量时，在测量达到一定深度且穿越高阻层后，土壤电阻率一般呈现下降趋势，此时最终测深需满足上述结论。例如，在测量某极址大地结构时，得到的数据显示土壤结构存在一个厚度约为20 km、平均电阻率在14000 Ω·m左右的高阻层，如果最后的穿透深度对应的土壤电阻率未降到880 Ω·m以下，则可认为测深不够，需要继续勘测。在工程应用中可通过表3估算临界电阻率以评价测深是否达到误差限定范围。在实际测量中，可以根据本文提供的方法针对具体土壤特性以及设定不同误差限定值进行建模评估。

本文对高阻层的起始深度高于表1所示的情况也进行了计算，计算结果如图5所示。结果显示，高阻层起始深度的增加会使临界电阻率的值更为宽裕，故对于深度更深的高阻层，表3的结果更为保守。

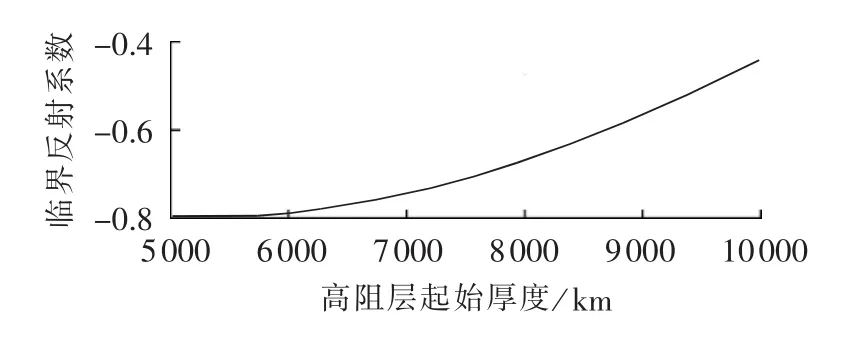
图5 高阻层起始厚度对临界反射系数的影响Fig.5 Effect of initial depth of high resistivity layer on critical reflection coefficient

整个地壳平均厚度约为17 km，大陆地壳平均厚度约为39～41 km。高山、高原地区地壳最高可达70 km，平原、盆地地壳相对较薄。地壳以下为上地幔，上地幔中有岩石圈和软流层，软流层中存在岩浆。鉴于此，在工程中，本文推荐MT法的测深为70 km，再根据临界电阻率评价测试结果。

2.3 极址土壤勘测方法

MT法广泛应用于矿产勘探，为测量接地极深层大地电阻率提供了方便。该方法是建立在大地电磁感应原理基础上的电磁测量方法，场源是天然的交变电磁场。MT法工作时，在同一点和同一时刻连续记录电场的2个相互垂直的水平分量Ex和Ey，以及磁场的3个互相垂直的分量Hx、Hy和Hz，通过计算处理得到该点的波阻抗Z，布线方法如图6所示。

由于土壤局部的不均匀性，在对极址进行勘探时，需要对待选极址附近多个点进行测量。根据2.1和2.2节的结论，选取的测点在距离直流接地极70 km的范围内，推荐测深为70 km，并根据临界电阻率对测试结果进行评估。由于距离直流接地极近的位置的土壤中浅层电流百分数高于远处，因此距离近的测点的参考价值更大，在选点时可以增加近处测点数目，本文推荐在距离待选极址20 km处选取3个测点，分别位于待选极址正北、西南、东南方向；50 km处选取2个测点，分别位于待选极址正南、西北方向；70 km处选取1个测点，位于待选极址东北方向。

在取得MT法测试原始数据并进行处理后，得到频率和视在电阻率曲线，运用MT法反演理论进行土壤层状结构反演，此时可以将各测点所得频率和视在电阻率的值放在一起进行综合反演，使得总体反演的均方根误差最小，从而得到用以评估直流接地极性能的土壤模型。

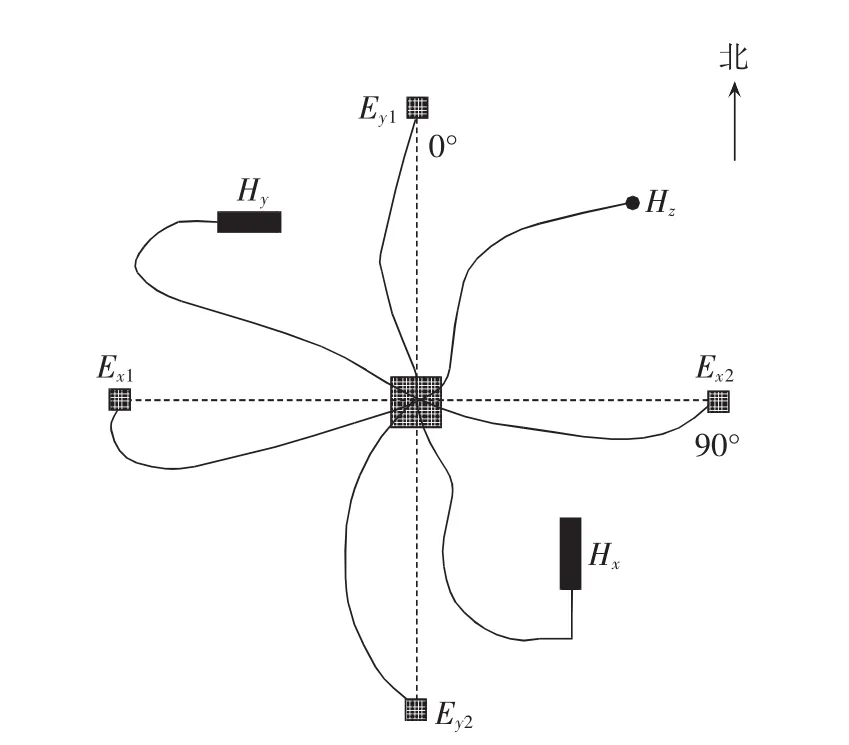
图6 MT法布线方案Fig.6 Wiring arrangement of MT method

3 结论

a.从直流电流透深的角度，研究了直流接地极极址土壤勘测时的测量范围。推荐测量待选极址周围70 km范围内表层到深层土壤的大地电阻率。

b.从直流偏磁计算的角度，在典型土壤的基础上，研究了直流接地极极址土壤勘测时的测量深度。土壤测深必须穿透高阻层，直到电阻率下降到临界电阻率以下，否则会给直流接地极影响的评估带来显著误差。推荐测深为70 km并根据临界电阻率评估测量深度是否满足误差要求。

c.提出MT法测量时推荐的布点方法。在距离待选极址20 km处选取3个测点，50 km处选取2个测点，70 km处选取1个测点，涵盖接地极各方向。

［1］梁旭明，张平，常勇.高压直流输电技术现状及发展前景［J］.电网技术，2012，36（4）：1-9.LIANG Xuming，ZHANG Ping，CHANG Yong.Recent advances in high-voltage direct-current power transmission and its developing potential［J］.Power System Technology，2012，36（4）：1-9.

［2］李杨，沈扬，周浩，等.长距离特高压交流输电线路单相接地故障过电压研究［J］. 电力自动化设备，2013，33（12）：98-104.LI Yang，SHEN Yang，ZHOU Hao，et al.Single-phase grounding overvoltage of long-distance UHVAC lines［J］.Electric Power Automation Equipment，2013，33（12）：98-104.

［3］王鹏，王奔，常晓.轻型直流输电系统鲁棒非脆弱H∞控制器设计［J］. 电力自动化设备，2013，33（12）：128-132.WANG Peng，WANG Ben，CHANG Xiao.Design of robust and non-fragile H∞controller for HVDC Light［J］.Electric Power Automation Equipment，2013，33（12）：128-132.

［4］国家能源局.高压接地直流极技术导则 ：DL /T437—2012［S］.北京：中国电力出版社，2012.

［5］郭剑.直流接地极对电气化铁路的电磁影响［J］.高电压技术，2013，39（1）：241-250.GUO Jian.Electromagnetic influences of ground electrode on electrified railway［J］.High Voltage Engineering，2013，39 （1）：241-250.

［6］赵志刚，刘福贵，程志光，等.HVDC中直流偏磁电力变压器叠片铁心损耗及磁通分布［J］. 高电压技术，2010，36（9）：2346-2351.ZHAO Zhigang，LIU Fugui，CHENG Zhiguang，et al.Lass and flux distribution of power transformer laminated core under DC biased magnetization condition in HVDC［J］.High Voltage Engineering，2010，36（9）：2346-2351.

［7］余洋，韦晨，朱林.直流输电接地极电流对不同结构变压器影响研究［J］. 电力系统保护与控制，2010，38（24）：71-76.YU Yang，WEIChen，ZHU Lin.ImpactofHVDC ground electrode current on transformers with different structures ［J］.Power System Protection and Control，2010，38（24）：71-76.

［8］鲁海亮，文习山，蓝磊，等.变压器直流偏磁对无功补偿电容器的影响［J］. 高电压技术，2010，36（5）：1124-1130.LU Hailiang，WEN Xishan，LAN Lei，et al.Impact of transformer DC bias on reactive compensation capacitor［J］.High Voltage Engineering，2010，36（5）：1124-1130.

［9］曾嵘，张波，赵杰，等.HVDC地中直流对交流系统的影响及规律分析［J］. 高电压技术，2009，35（3）：678-682.ZENG Rong，ZHANG Bo，ZHAO Jie，et al.Influence and characteristics analysis of effect of the HVDC ground return current on AC system［J］.High Voltage Engineering，2009，35（3）：678-682.

［10］陈德智，黄振华，刘杰，等.水平分层土壤中点电流源电流场的计算［J］. 高电压技术，2008，34（7）：1379-1382.CHEN Dezhi，HUANG Zhenhua，LIU Jie，et al.Calculation of current field due to a point source in multi-layer soil［J］.High Voltage Engineering，2008，34（7）：1379-1382.

［11］曹晓斌，胡劲松，余波，等.一类垂直双层土壤中地网接地电阻的简易计算公式［J］. 中国电机工程学报，2009，29（1）：120-126.CAO Xiaobin，HU Jinsong，YU Bo，et al.A simplified formula for grounding grids resistance in a type of vertical two-layer soil［J］.Proceedings of the CSEE，2009，29（1）：120-126.

［12］何俊佳，叶会生，林福昌，等.土壤结构对流入变压器中性点直流电流的影响［J］. 中国电机工程学报，2007，27（36）：14-17.HE Junjia，YE Huisheng，LIN Fuchang，et al.Influence of soil structure on direct current flowing into neutral point of power transformer［J］.Proceedings of the CSEE，2007，27（36）：14-17.

［13］刘曲，李立浧，郑健超.复合土壤模型下HVDC系统单极大地运行时的电流分布［J］. 中国电机工程学报，2007，27（36）：8-13.LIU Qu，LI Licheng，ZHENG Jianchao.DC currents distribution in HVDC systems of monopolar operation with ground return in complex soil structure［J］.Proceedings of the CSEE，2007，27（36）：8-13.

［14］刘曲，李立浧，郑健超.考虑海洋影响的直流输电单极大地运行时变压器中性点直流电流研究［J］. 电网技术，2007，31（2）：57-65.LIU Qu，LI Licheng，ZHENG Jianchao.Study on DC current through transformer neutrals caused by ground return operation mode ofHVDC system with sea influence considered ［J］.Power System Technology，2007，31（2）：57-65.

［15］解广润.电力系统接地技术［M］.北京：水利电力出版社，1991：1-247.

［16］潘卓洪，张露，谭波，等.高压直流输电入地电流在交流电网分布的仿真分析［J］. 电力系统自动化，2011，35（21）：110-115.PAN Zhuohong，ZHANG Lu，TAN Bo，etal.Simulation and analysis of HVDC earth-return current’s distribution in AC power grid［J］.Automation of Electric Power Systems，2011，35（21）：110-115.

［17］潘卓洪，张露，林进弟，等.多层水平土壤对交流电网直流分布的影响［J］. 高电压技术，2012，38（4）：855-862.PAN Zhuohong，ZHANG Lu，LIN Jindi，etal.Influence of horizontal multi-layer soil on DC current distribution in AC power grid［J］.High Voltage Engineering，2012，38（4）：855-862.

［18］陈虎，张英敏，贺洋，等.特高压交流对四川电网多送出直流输电系统影响评估［J］. 电力系统保护与控制，2011，39（7）：136-141.CHEN Hu，ZHANG Yingmin，HE Yang，et al.Impact assessment of UHVAC on multi-send HVDC systems of Sichuan Power Grid［J］.Power System Protection and Control，2011，39 （7）：136-141.

［19］苏杰，吴广宁，曹晓斌，等.应用可控源音频大地电磁法的土壤电阻率测量［J］. 电网技术，2011，35（1）：141-145.SU Jie，WU Guangning，CAO Xiaobin，et al.Analysis on soil resistivity measurementbased on controlled source audiofrequency magneto-telluric［J］.Power System Technology，2011，35（1）：141-145.

［20］徐华.大型变电站接地网的参数计算和优化设计［D］.武汉：武汉大学，2004.XU Hua.The parameters calculaiton and opitmum design of grounding grids of large substation［D］.Wuhan：Wuhan University，2004.

［21］郭剑，邹军，何金良，等.水平分层土壤中点电流源格林函数的递推算法［J］. 中国电机工程学报，2004，24（7）：105-109.GUO Jian，ZOU Jun，HE Jinliang，et al.Recursive method to obtain analytic expressions of green’s functions in multi-layer soil by computer［J］.Proceedings of the CSEE，2004，24（7）：105-109.