规模化并网逆变器网侧谐振电流信息的小波包提取方法

肖华锋 ，刘隰蒲 ，过 亮 ，王 彤

（1.东南大学 电气工程学院，江苏 南京 210096；2.南京南瑞集团公司，江苏 南京 211106）

0 引言

基于电压源型并网逆变器的可再生能源规模化接入电网的应用日益广泛，如我国西部的大型光伏电站集中并网、欧洲国家的大量户用光伏并网逆变器在配网末端接入电网等。在这些应用中，多个并网逆变器的输出端在电网的公共端PCC（Point of Common Coupling）并接，由各并网逆变器开关动作激发并网滤波器产生的谐振在PCC汇合，导致各并网支路和PCC的电流谐振加剧，从而危及并网逆变器和电网的运行安全［1-2］。

在现有的抑制措施中，有源阻尼技术被认为是解决滤波器谐振的理想方案［3］，但现有研究多是在单机并入理想电网的情况下进行的分析、设计和验证，在实验测试中也都能满足相关标准对进网电流质量的要求。而在实际应用中的情况是：以户用光伏并网逆变器为例，大量的并网逆变器单机在配网末端接入低压电网，PCC表现出弱网特性［4］，故电网不能简单地等效为理想电压源；另外，多个单机在PCC并联，原来各自的谐振源相互作用，同时考虑附近的容性负荷，将产生更复杂的谐振现象［2］。这使得带阻尼措施的单机在规模化应用中仍然存在谐振，即单机满足进网要求，而规模化应用后进网电流质量恶化，甚至出现异常。

为了有效解决规模化并网逆变器的谐振问题，本文首先介绍一种采用对动态谐振量进行“检测-反馈-补偿”的闭环抑制方案。若要成功实现对动态谐振电流的闭环抑制，准确实时地获取谐振电流信息是关键，如同有源滤波器系统中的补偿参考信息一样重要。在单相系统中对单次谐波电流检测的方法主要有虚拟三相信号法、Hilbert变换法［5］和离散傅里叶变换法［6］等，这些方法对稳定的谐波电流均有较好的检测效果。鉴于规模化并网逆变器谐振电流的复杂多变性，常规的谐波电流提取方法将难以应付，而且其动态响应速度慢。

小波变换技术在电力电子技术中的应用目前还处于探索和起步阶段［7-11］，文献［12］是较早将小波变换用于有源滤波器谐波电流补偿基准产生的研究，其思路是通过小波变换提取出基波电流信息再与总电流进行相减从而得到所有的谐波电流成分，并以此作为补偿基准；文献［13］采用小波包变换直接提取有源电力滤波器的谐波补偿基准，从仿真结果看仅实现了低次谐波直接提取的目标，且运算量偏大，实时性较差。可以看出，小波分解只能在低频段无限重复分解，在得到了高频的时间分辨率和低频的频率分辨率的同时丢失了低频的时间分辨率和高频的频率分辨率。即小波对信号频带是不均匀划分，具有高频频带宽而低频频带窄的特点，导致高频信号的检测精度降低，使得其在一些应用场合受限［14-15］。而小波包分解可以得到全频段均匀的时间分辨率和频率分辨率，但由于计算量的增加使得在实时系统中的应用受限。

本文针对规模化并网逆变器系统谐振电流频次、幅值和频率分布范围的时变特性，提出一种基于db4小波包的小波树优化分解与重构算法，以实时提取谐振电流中最大谐振分量为目标，在保证分解精度的同时减少了计算量，使得算法的实用性得到提高。本文详细讨论了优化算法中小波频段选取方法、信号采样频率的选取方法，并分析了基于小波树的分解和重构过程。最后，基于DSP+FPGA控制平台在含不同谐振电流信息的情况下对算法进行了验证，实验结果表明了优化算法的有效性。

1 规模化并网逆变器网侧谐振电流抑制原理

带有谐振抑制功能的单相并网逆变器系统结构如图1所示。其中，iINV为逆变器侧电流；ug为PCC处电压；ig为网侧电流；为基波电流调节器的给定。进网基波电流控制由电网电压锁相环模块和基波电流调节器实现，与常规逆变器一致。而并网引起的谐振电流成分由小波包算法实时提取出最大成分再送入谐振电流调节器产生谐振抑制力，并经由PWM模块和逆变桥产生谐振抑制电压作用至谐振网络上抑制该并网支路的谐振电流。

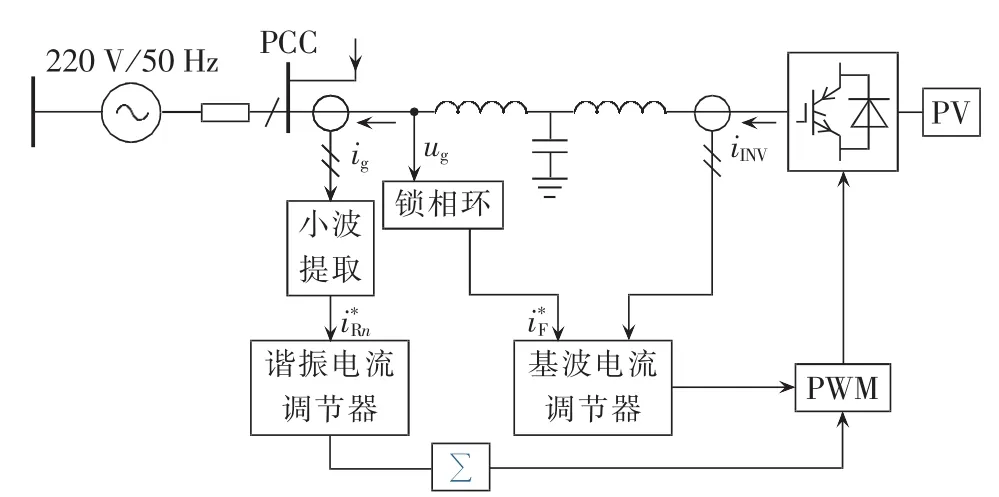
图1 基于小波提取的并网逆变器谐振抑制系统结构Fig.1 Configuration of grid-connected inverter resonance restraint system based on wavelet extraction

在此特别说明的一点是，谐振电流调节器的输出量是以累加的方式加入PWM调制信号中的，这样在有新的谐振成分出现后，谐振电流调节器可以专一地抑制该新的谐振成分，原谐振成分的抑制作用仍然存在。通过在PCC各支路的并网逆变器上加入该谐振抑制策略，就可消除各支路中的谐振电流，由基尔霍夫电流定律可知送入配电网的电流将为基波电流。

2 网侧电流谐振信息的小波包分析方法

2.1 小波包滤波器组的结构

根据谐振电流频域分布特点，利用小波包频域频带滤波特性就可以实现基波和谐波的频带区分；利用小波包分析的时域局部特性就可以实时地跟踪谐振电流信息。

设网侧电流 ig∈L2（R），即属于 Hilbert空间，占据频域空间V0，低频子空间Vj与高频子空间Wj是前一层子空间Vj-1或Wj-1的正交分解，则V0可表示为：

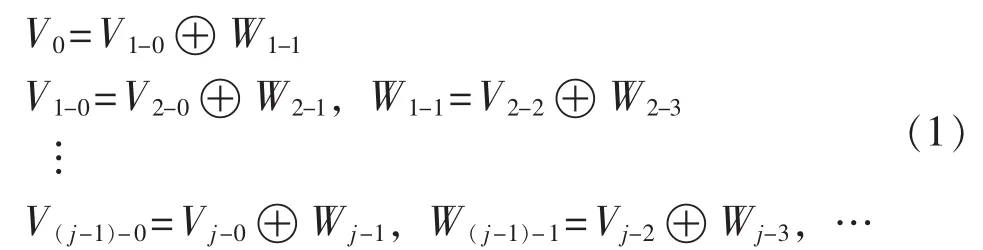
其中，j∈Z；符号⊕表示直和。谐振分量所在子空间Wj-1、Vj-2、Wj-3、…、Vj-（2j-2）、Wj-（2j-1）可以逐级逼近总谐振电流iR的频域空间，分解的频带范围越宽，各子带重构分量的和越接近iR。与式（1）的频域分解相对应，ig在时域可以表示为基波和谐振分量的和，即：

其中，iF为基波分量；iR为各次非平稳谐振分量之和。

可以看出，小波包分析在小波分析的基础上对高频段进行了再分解，以获得更高的频率分辨率，从而实现将当前各次谐振电流分量的频带均匀分解开；再对含最大谐振幅值的谐振电流信息所在的子空间进行重构，将使得含最大谐振幅值的谐振信息i*Rn从原始信号ig中提取出来。以该谐振电流信息为基准，便可以通过谐振电流调节器和逆变桥产生抑制谐振电流的作用力。

设正交小波基的滤波器系数分别为hn和gn，尺度函数为 φ（t），小波函数为 ψ（t）。φ（t）和 ψ（t）的二尺度方程为：

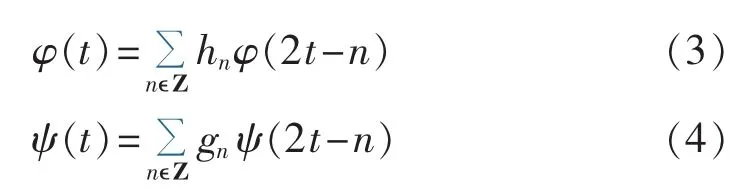
根据信号分解和重构的Mallat算法可以得到式（5）—（7）。

（1）分解算法。

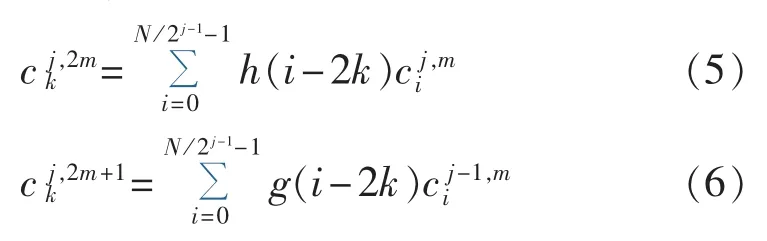
（2）重构算法。

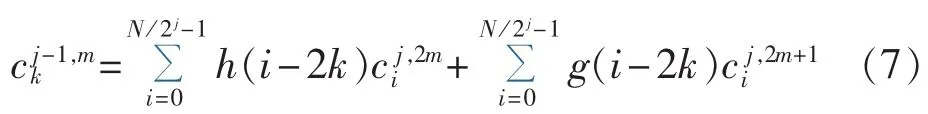
其中，j=1，2，…，J，为小波分解层数；k=0，1，…，N /2j，为第j层分解系数，N为采样数据总长度；m=0，1，…，2j-1，为第j层分解的频段序号。

在实际应用中，第0层信号为采样所得信号。卷积因子 h（k）、g（k）由具体的小波基决定。 每一层信号由上一层小波信号与卷积因子卷积得到。考虑到采用常规滤波器组结构直接分解每层小波会出现频带划分不按频率大小顺序连续排列的问题，本文采用将每一层高通和低频滤波器交替变换位置的方法加以修正［16］。小波包分解递推公式如图2所示。

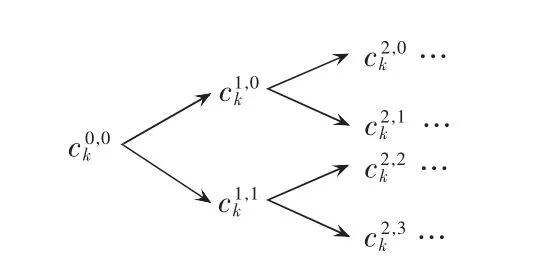
图2 小波包分解递推Fig.2 Recursive wavelet packet decomposition

2.2 小波包基的选择

小波变换的本质是测量小波波形与被分析信号波形的局部相似程度。要想使小波变换方法取得成功，应根据被分析信号的特点选择最适合的小波。为了分解出时变的谐振电流信息，有2种选择合适小波的途径：小波与谐振信号匹配，小波与基波信号匹配。本文采用小波包变换直接实时提取谐振电流信息的方式，故按小波与谐振信号匹配的途径选择小波包基。

由于谐振电流在频域中具有类似高斯窗函数的外形，而Daubechies小波在频域也具有类似特征，且具备时频局部化和时频紧支性的特性。经过仿真对比，本文选择Daubechies 4（db4）作为小波包基。

2.3 小波树优化分解算法

在本文提出的规模化并网逆变器谐振抑制控制策略中，不需要同时对所有谐振电流成分进行全补偿，但对谐振信息检测的实时性要求很高。因此，小波包完全分解方法不适用。本文提出始终抑制当前最大谐振电流幅值所在频段的谐振电流，并保持抑制力的积累，如此持续下去可快速有效地抑制全频段的谐振电流；并可降低每次谐振电流信息提取的运算量，从而保证提取的快速性。

本文提出的小波包分解的核心步骤是：根据谐振电流信号特性确定合适的谐振能量表征量，按该表征量对上一层分解结果判定哪一频段应进一步细分出它的高频部分与低频部分（为小波频段），哪些频段无需继续细分（为保持频段或置零频段）。这样得到的小波包对应的频带结构将是与欲被分解的含最大谐振幅值信号相匹配的频带结构。上述自适应目标频段的优化小波包分解树方法流程如下。

（1）小波分解是否已经达到设定的最高分解层数。若是，则停止分解，并将最低频段标识为置零频段；若否，则继续分解，对上一层分解系数进行小波变换后得到分解系数

（2）将分解系数按式（8）运算得到该层各个频段的谐振能量因子

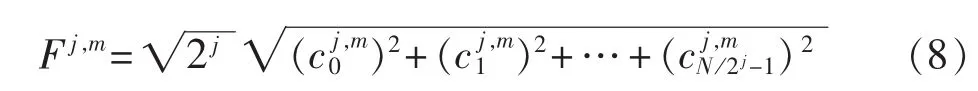
（3）寻找该层各个频段中次大的谐振能量因子

设该段小波系数是否需要在下一层继续分解的指示函数为 Sj，m，则：

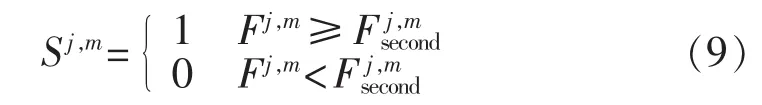
为了平衡误分解（不该分解的频段被分解）和未分解（应该分解的频段未被分解）带来的计算量增加和误差，在谐振能量因子Fj，msecond中引入反比于层数j的比例因子k，使得当层数j较小时减少未分解，层数j较大时减少误分解。

（4）Sj，m标识为0的小波段在下一层小波分解时停止分解，并标识为保持频段；Sj，m标识为1的小波段则从步骤（1）继续分解，并标识为小波频段。

对谐振电流信息重构则根据分解路径以及上一层 Sj，m的标识按式（7）进行逆向计算。

2.4 采样频率的选取

根据光伏电站现场测试数据和模拟仿真数据得到规模化并网逆变器系统谐振频率的变化范围在0.5～3 kHz［17-19］。 根据香农采样定理可得谐振电流频率在3 kHz时采样频率应大于6 kHz；根据信号重构的要求，电网基波频率和谐振频率应分在2个不同频率段，故每个频段范围要小于0.5 kHz，当分解层数J=4时（共16个频段）可覆盖的频率范围最大为8 kHz，则要保证采样频率不高于16 kHz。设y为小波分解后重构的信号、y*为原始信号，重构误差为：

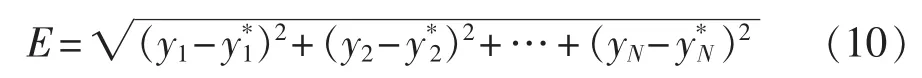
其中，N为采样点数。

设待检测谐振电流频率为800Hz，通过对不同采样频率下的数据进行分解重构，按式（10）计算误差可得图3所示的重构误差曲线，图中N=512，纵坐标为各采样点的标幺化误差累积。

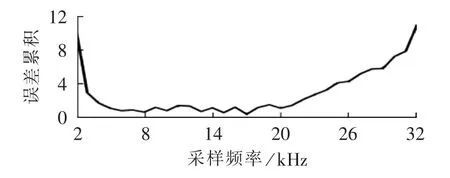
图3 不同采样频率下谐振电流信息提取重构误差Fig.3 Curve of resonant current extraction-reconstruction error vs.sampling frequency

考虑重构误差和采样资源消耗，采样频率在6～8 kHz区间比较合适，本文选择采样频率Fs=8 kHz。

3 网侧电流谐振信息的分解、重构过程分析

3.1 谐振电流信息提取过程

在Fs=8 kHz、J=4条件下小波包完全分解的分解树如图4（a）所示。由香农采样定理可得，在小波分解第四层时，小波段的分辨率为250 Hz，范围是0～4 kHz。 按式（3）和（4）的定义，将完全分解中乘法运算的数量作为参考指标Cw（它与采样点数、滤波器长度和分解层数正相关），令小波树完全分解时Cw=1。通过计算本文所提优化算法在分解不同谐振频率成分时的Cw数值可量化优化算法运算量的减少程度。

当谐振电流频率为800Hz时，本文提出的优化小波包分解树如图4（b）所示，可计算出运算量指标Cw=0.59，计算量明显减少。若谐振电流频率为2 000 Hz，详细的优化分解路径如图4（c）所示，可计算出Cw=0.78。综上可以看出，相比完全分解算法，本文提出的小波树优化算法能不同程度地减少运算量，且不损失期望的最大谐振电流信息。

图4 小波包全分解与优化分解树Fig.4 Complete wavelet packet decomposition and optimized decomposition tree

3.2 谐振电流信息的重构过程

在小波树优化算法中，重构为分解的逆过程，根据式（7）可以得到重构后的波形（小波树优化算法中未进行分解的频段同时也减少了该层重构的计算量），由于小波包分解对最大谐振信号的信息没有损失，故能实现含最大幅值谐振波形的完整重构。

4 谐振电流信息提取算法的实验结果

为了进一步验证本文提出的小波树优化算法在谐振电流信息分解与重构过程中的有效性，进行了不同谐振情况下的谐振电流提取性能的验证。小波分解参数为 Fs=8 kHz、J=4、N=512，选取 db4 小波作为小波包基。由于小波算法中含有大量卷积运算，若采用常规的串行执行处理器将耗时较多，本项目采用FPGA进行小波算法的并行执行以减少单次运算时间。为此构建DSP+FPGA数字运算平台，其中DSP负责谐振电流信息采集、数据调理及轮转传输至FPGA，以及并网逆变器的进网电流实时控制；FPGA负责小波核心算法的运算，本文提出的小波分解重构算法执性一次的时间约130 μs，保证了算法的实时性。进网电流的谐振成分由交流可编程源进行模拟和设定。

图5为进网电流含单一800 Hz谐波成分时的电流采样信号和谐振电流信息提取波形，可以看出算法能较快速和平稳地跟踪谐振电流信息。

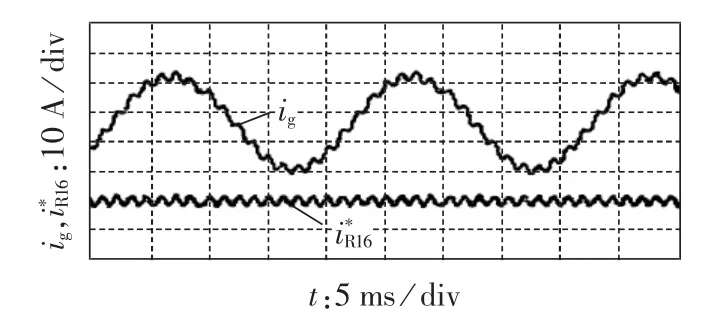
图5 含800 Hz谐振频率成分时的谐振电流信息提取结果Fig.5 Information extraction result of resonant current with 800 Hz component

图6为进网电流含800 Hz和2000 Hz谐波成分时的电流采样信号和谐振电流信息提取波形，此时，设置的2000 Hz谐波成分幅值为800 Hz谐波幅值的2倍。可以看出提取结果的波形频率为2000 Hz，与期望一致，验证了选取算法的有效性。

图7 为进网电流含 800 Hz、2000 Hz、2700 Hz和3600 Hz谐波成分时的电流采样信号和谐振电流信息提取波形，此时，设置的800 Hz谐波成分幅值最大。可见提取结果的波形频率主要为800 Hz，与期望一致，验证了选取算法在多分解频段选取中的有效性。

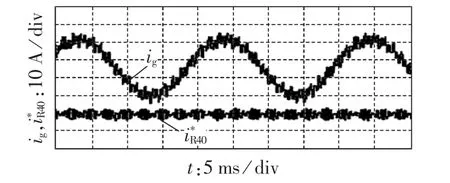
图6 含800 Hz和2000 Hz谐振频率成分时的最大谐振电流信息提取结果Fig.6 Information extraction result of maximum resonant current with 800 Hz and 2000 Hz components

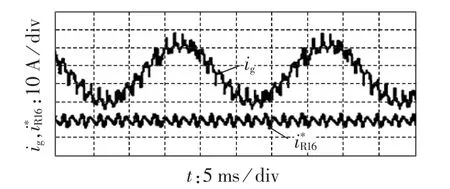
图7 含 800 Hz、2000 Hz、2700 Hz和 3600 Hz谐振频率成分时的最大谐振电流信息提取结果Fig.7 Information extraction result of maximum resonant current with 800 Hz，2000 Hz，2700 Hz and 3600 Hz components

5 谐振电流抑制的实验结果

为了验证本文提出的谐振信息在谐振电流抑制中的实际效果，采用并网逆变器的LCL谐振来模拟电网引起的电流谐振，谐振电流成分主要在800 Hz左右，通过“检测-反馈-补偿”思路进行抑制。图8（a）、（b）分别为抑制算法起作用前后的波形图，可以看出谐振电流得到了较好的抑制，验证了本文提出的谐振信息小波提取算法的有效性，可用于实时控制系统。

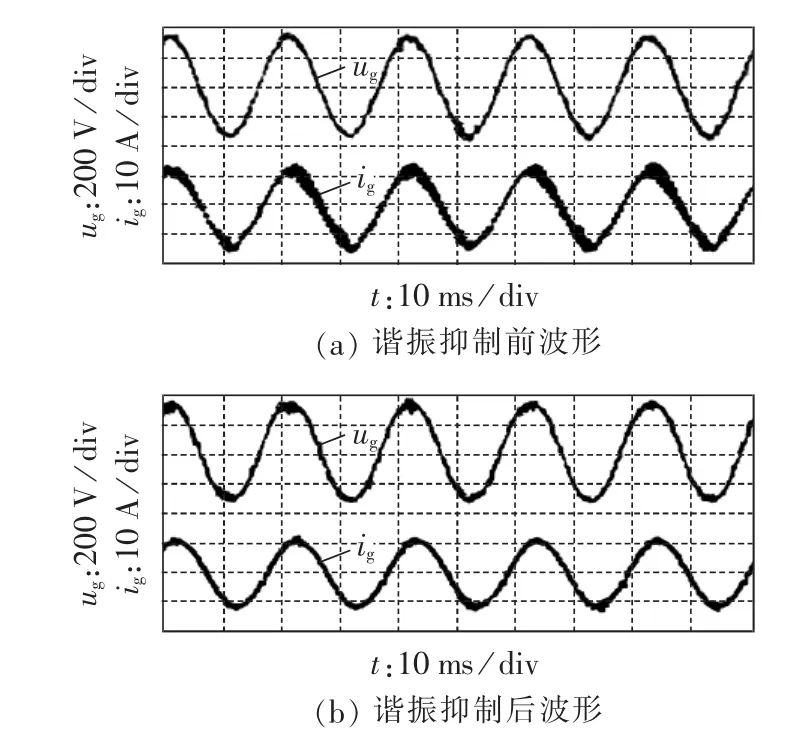
图8 谐振抑制效果Fig.8 Effect of resonance restraint

6 结论

本文针对规模化并网逆变器运行中存在的谐振现象，研究谐振电流信息的提取技术，提出采用db4小波包直接提取最大谐振电流成分，主要结论如下：

a.提出基于小波树优化的分解和重构算法，可降低运算量且不损失期望信息的信息量，该算法不仅能对时域进行定位，而且能够动态调整频率适应范围；

b.基于DSP+FPGA控制平台进行了小波包算法的验证，单次运算时间在百微秒级，使得小波包算法能应用于实时控制系统；

c.本文提出的算法可应用于有源滤波器补偿基准产生和电能质量实时分析等场合。

［1］TEODORESCU R，LISERRE M，RODRIGUEZ P.Grid converters for photovoltaic and wind power systems［M］.Chichester，United Kingdom：Wiley，2011：1-4.

［2］ENSLIN J H R，HESKES P J M.Harmonic interaction between a large number of distributed power inverters and the distribution network［J］.IEEE Transactions on Power Electronics，2004，19（6）：1586-1593.

［3］HATUA K，JAIN A K，BANERJEE D，et al.Active damping of output LC filter resonance for vector-controlled VSI-fed AC motor drives［J］.IEEE Transactions on Industrial Electronics，2012，59（1）：334-342.

［4］LISERRE M，TEODORESCU R，BLAABJERG F.Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values［J］.IEEE Transactions on Power Electronics，2006，21（1）：263-272.

［5］RASHID A.IIR discrete-time Hilbert transformers［J］.IEEE Transactions on Acoustics，Speech，and Signal Processing，1987，35（8）：1116-1119.

［6］TONG X Q，SHEN M，YIN J.Single order harmonic detection with incremental algorithm of DFT［C］∥Proceedings of the IPEMC.Wuhan，China：IEEE，2009：2402-2405.

［7］胡国胜，任震，黄雯莹.小波变换在电力系统中应用研究［J］.电力自动化设备，2002，22（3）：71-78.HU Guosheng，REN Zhen，HUANG Wenying.Application of wavelet transform to electric power system［J］.Electric Power Automation Equipment，2002，22（3）：71-78.

［8］POISSON O，RIOUAL P，MEUNIER M.Detection and measurement of power quality disturbances using wavelet transform ［J］.IEEE Transactions on Power Delivery，2000，15（3）：1039-1044.

［9］FENG Guihong，ZHANG Haining，ZHUANG Fuyu，et al.Research on extraction of partial discharge feature signal based on complex wavelet for power transformer［C］∥International Conference on Electrical Machines and Systems. Seoul，Korea：IEEE，2007：1269-1273.

［10］陈伟根，杜杰，凌云，等.变压器油纸绝缘气隙放电能量-小波矩特征及放电过程划分［J］. 电力自动化设备，2014，34（6）：89-95.CHEN Weigen，DU Jie，LING Yun，et al.Energy-wavelet moment characteristics of air-gap discharge in oil-paper insulation of transformer and partition of discharge process［J］.Electric Power Automation Equipment，2014，34（6）：89-95.

［11］刘可真，束洪春，于继来，等.±800 kV特高压直流输电线路故障定位小波能量谱神经网络识别法［J］.电力自动化设备，2014，34（4）：141-147.LIU Kezhen，SHU Hongchun，YU Jilai，et al.Fault location based on wavelet energy spectrum and neural network for±800 kV UHVDC transmission line［J］.Electric Power Automation Equipment，2014，34（4）：141-147.

［12］邵明，钟彦儒，余建明.基于小波变换的谐波电流的实时检测方法［J］. 电力电子技术，2000，34（1）：42-45.SHAO Ming，ZHONG Yanru，YU Jianming.Measurement for realtime detecting harmonic current based on wavelet transform［J］.Power Electronics，2000，34（1）：42-45.

［13］李鹏飞，张海燕.基于小波包变换有源电力滤波器的研究［J］.电气传动自动化，2007，29（5）：16-18.LI Pengfei，ZHANG Haiyan.Study of active power filter based on wavelet package transform［J］.Electric Drive Automation，2007，29（5）：16-18.

［14］周林，夏雪，万蕴杰，等.基于小波变换的谐波测量方法综述［J］.电工技术学报，2006，21（9）：67-74.ZHOU Lin，XIA Xue，WAN Yunjie，et al.Harmonic detection based on wavelet transform［J］.Transactions of China Electrotechnical Society，2006，21（9）：67-74.

［15］黄文清，戴瑜兴，全慧敏.基于Daubechies小波的谐波分析算法［J］. 电工技术学报，2006，21（6）：45-53.HUANG Wenqing，DAI Yuxing，QUAN Huimin.Harmonic estimation method based on Daubechies wavelet［J］.Transactions of China Electrotechnical Society，2006，21（6）：45-53.

［16］薛蕙，杨仁刚，罗红.利用小波包变换实现电力系统谐波分析［J］. 电网技术，2004，28（5）：41-45.XUE Hui，YANG Rengang，LUO Hong.Power system harmonic analysis using wavelet packet transform［J］.Power System Technology，2004，28（5）：41-45.

［17］谢宁，罗安，陈燕东，等.大型光伏电站动态建模及谐波特性分析［J］. 中国电机工程学报，2013，33（36）：10-17.XIE Ning，LUO An，CHEN Yandong，et al.Dynamic modeling and characteristic analysis on harmonics of photovoltaic power stations［J］.Proceedings of the CSEE，2013，33（36）：10-17.

［18］赵伟，姜飞，涂春鸣，等.电动汽车充电站入网谐波分析［J］.电力自动化设备，2014，34（11）：61-66.ZHAO Wei，JIANG Fei，TU Chunming，et al.Harmonic currents of grid-connected EV charging station［J］.Electric Power Automation Equipment，2014，34（11）：61-66.

［19］周林，张密.大型光伏电站谐振现象分析［J］.电力自动化设备，2014，34（6）：8-14.ZHOU Lin，ZHANG Mi.Analysis of resonance phenomenon in large-scale photovoltaic power plant［J］.Electric Power Automation Equipment，2014，34（6）：8-14.