矩阵方程X−ATX−1A=Q的牛顿迭代解法∗

程可欣,彭振赟,杜丹丹,肖宪伟

(桂林电子科学大学数学与计算科学学院广西高校数据分析与计算重点实验室，桂林 541004)

1 引言

非线性矩阵方程

其中A∈Rn×n，Q为n×n阶正定阵，在控制理论、动态规划、插值理论和随机滤波等领域中具有广泛的应用[1-3]．例如，很多具有实际应用的偏微分方程问题进行离散化处理后，需要求解线性方程组[4]M x=f，其中

其中Q是对称正定矩阵．若将系数矩阵M分解为

则对称正定矩阵X必须是非线性矩阵方程(1)的解．一旦将系数矩阵M分解为上述形式，那么，利用Woodbury公式[5]就可以有效地求得线性方程组M x=f的解．

关于这类非线性矩阵方程问题的研究文献有很多，如Zhan和Xie[1]给出了方程X+ATX−1A=I有正定解的条件及计算极解的无求逆迭代算法．Engwerda[6,7]给出了矩阵方程X+A∗X−1A=Q正定解存在的条件，并提出了计算其极解的递归算法．Ferrante,Levy[2]和Mein[8]分别研究了矩阵方程X=Q+NX−1N∗和X −A∗X−1A=Q矩阵方程，给出了计算其极解的不动点迭代算法．刘新国[9]给出了求解矩阵方程I=X+AHX−1A的简单迭代并进行误差估计分析．Ramadan和EIShazly[10]给出了方程有正定对称解的充要条件，以及计算其解的不动点迭代算法．Peng等[11]给出了计算方程X+A∗X−αA=Q(0< α≤1)的极解的无求逆迭代算法，并讨论了算法的收敛性问题．段雪峰和廖安平[12]给出了矩阵方程X+A∗X−qA=Q(q≥1)有解的条件同时给出了解的误差估计式．Liu和Zhang[13]研究了利用牛顿迭代法求解矩阵方程X=Q+AH(I⊗X−C)−1A，并给出了解的误差估计．关于矩阵方程X±A∗X−1A=Q的解的扰动问题，在文献[14–16]中进行了比较系统地讨论．

本文研究矩阵方程X−ATX−1A=Q的牛顿迭代解法．在给定初值的条件下，证明了迭代方法产生的矩阵序列包含在确定的闭球内并收敛到闭球内唯一的矩阵方程的解，同时给出了近似解与真解的误差估计式．此外，还给出了说明算法有效性的数值例子．

记号：Rn×n表示阶矩阵的集合，I表示n阶单位阵，AT表示矩阵A的转置，∥A∥F表示矩阵A的Frobenius范数，∥A∥表示矩阵A的谱范数，A⊗B表示矩阵A和B的K ronecker积．

2 牛顿迭代法及其收敛性

将正定矩阵Q做Cholesky分解，即Q=LTL，其中L∈Rn×n为n×n阶上三角阵，则矩阵方程(1)转化为

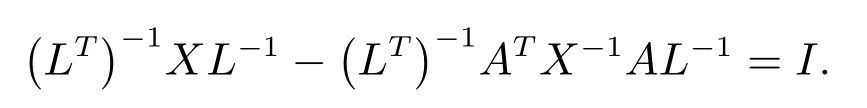
令Y=(LT)−1X L−1，则有X=LTYL．因而矩阵方程(1)等价于

其中P=(LT)−1AL−1∈ Rn×n．

记F(Y)=Y−PTY−1P−I，则求矩阵方程(2)的解等价于求方程F(Y)=0的解．注意到矩阵函数F(Y)在Y处方向为的Fréchet-导数为

牛顿法求解非线性矩阵方程(2)的迭代格式可以描述为如下算法1．

算法1(牛顿法求矩阵方程(2)的迭代格式)

第1步给出初始矩阵Y0=I，误差容许值ε>0．令k:=0；

第2步如果∥F(Yk)∥F≤ε停止；否则，求Ek∈Rn×n，使得；即求Ek∈Rn×n，使得E+BTEB=C，其中

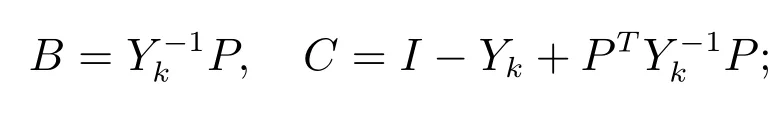
第3步计算Yk+1=Yk+Ek；

第4步置k=k+1，转第2步．

下面将讨论算法1的有关收敛性结果．首先给出如下引理．

引理1[13,17]设S,T ∈ Cn×n．若S可逆，且∥S−1∥≤β,∥S−T∥≤α,αβ<1，则T也可逆，且．

引理2对任意可逆矩阵X,Y有下列不等式成立

证明 对任意可逆矩阵X,Y和任意矩阵E有

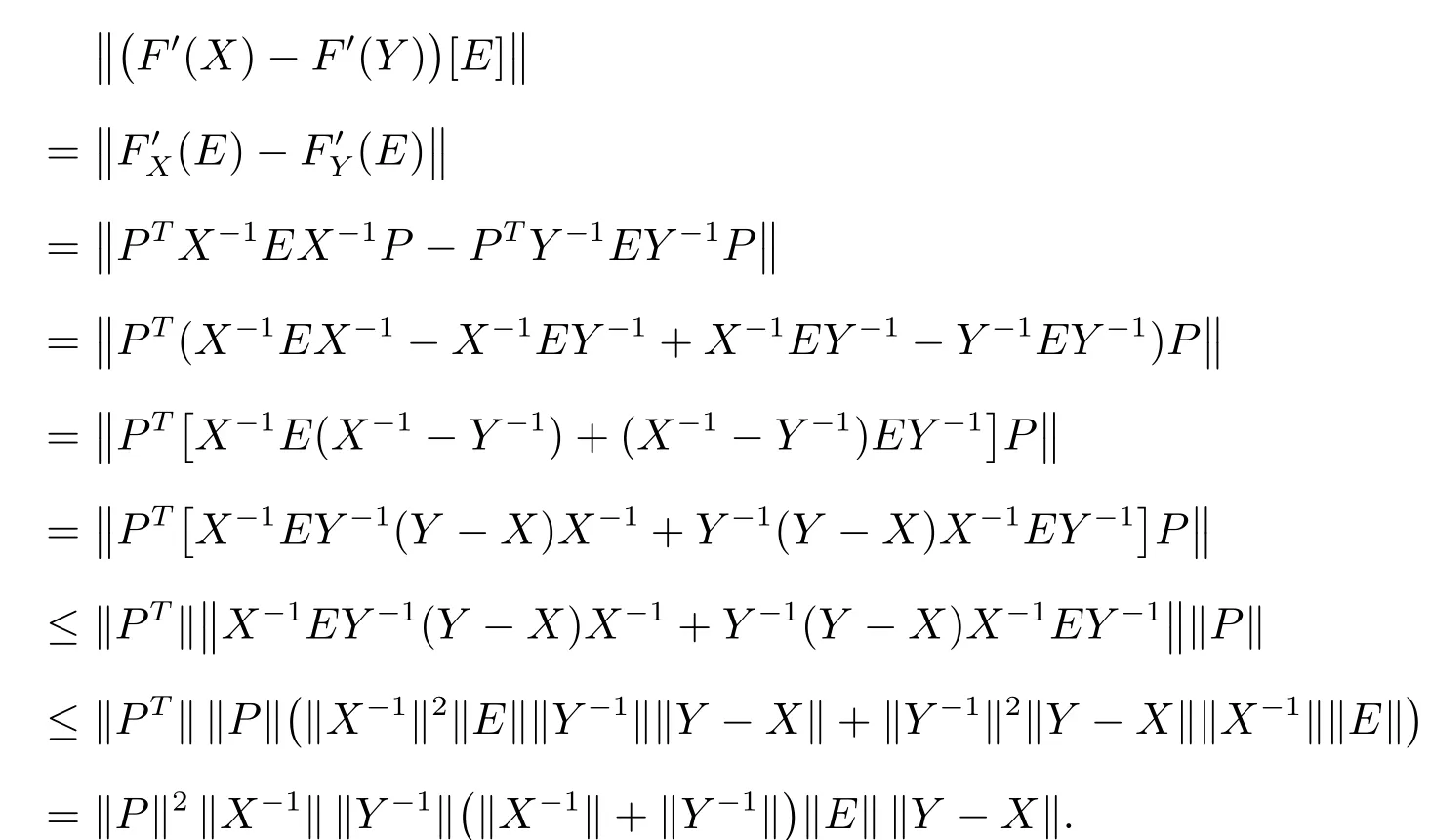
因此

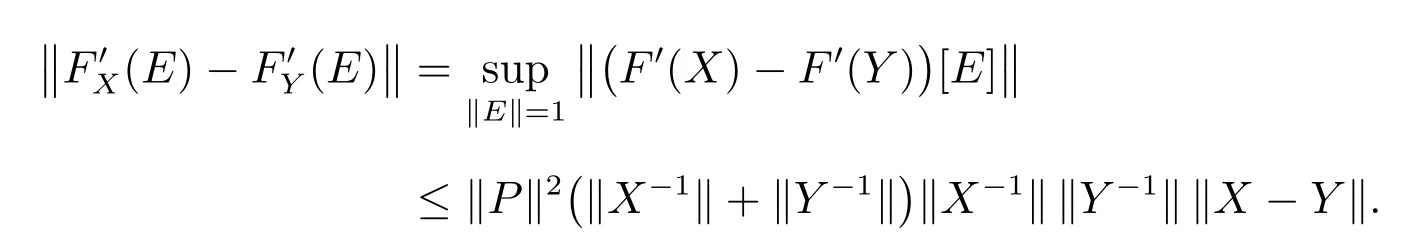
引理3假设Y0可逆，且有，则有

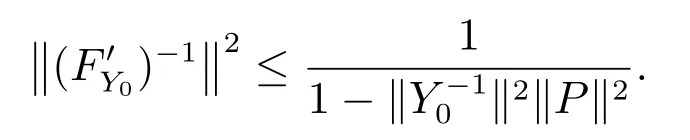
证明 由，可知

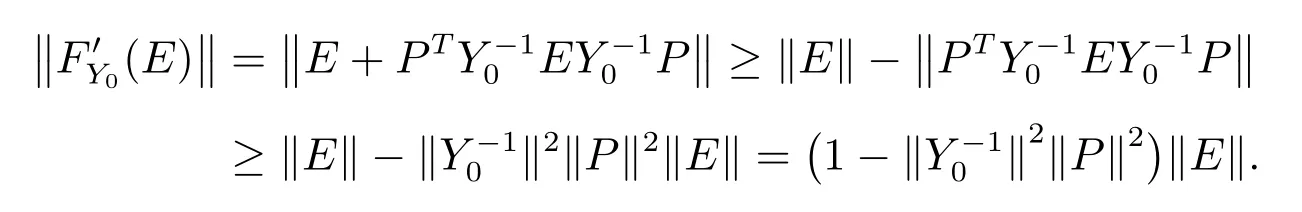
上式表明，当且仅当E=0．因此，矩阵

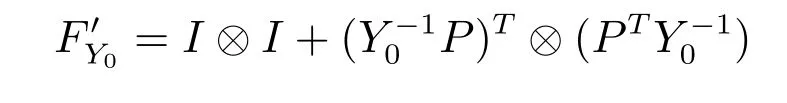
是可逆的，并且有

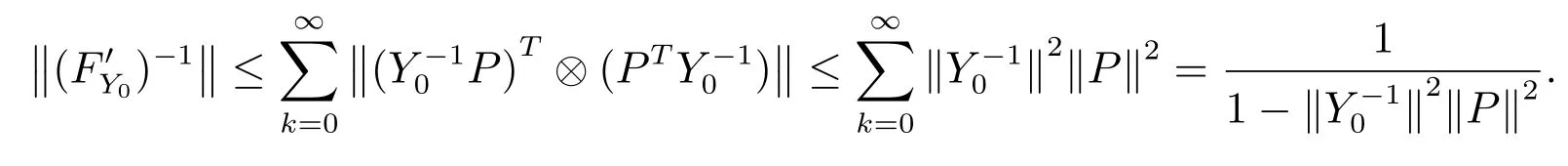
定义矩阵函数

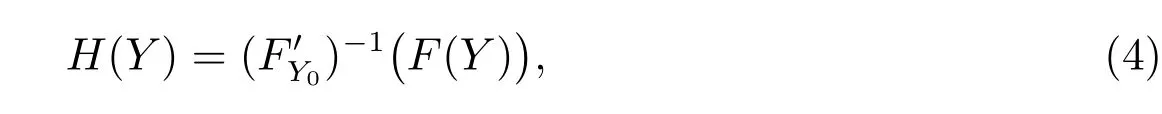
则

是恒等算子，且关于算子H(Y)的牛顿法生成的矩阵序列{Yk}与关于算法1生成的矩阵序列{Yk}是相同的，并且有如下引理．

引理4假设

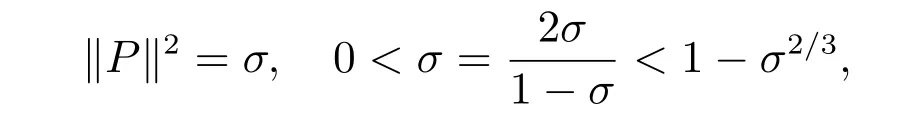
则当Y0=I时，下列结论成立：

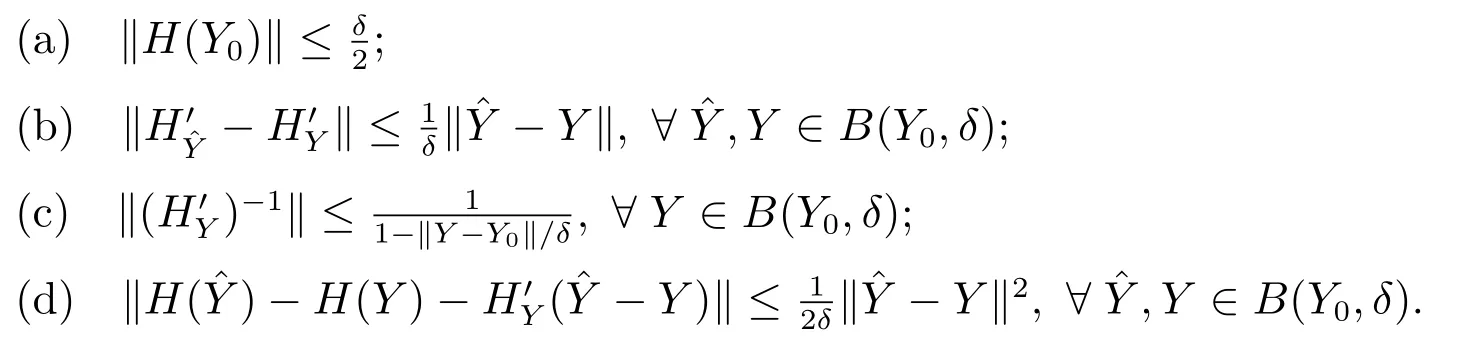
证明 (a)由于

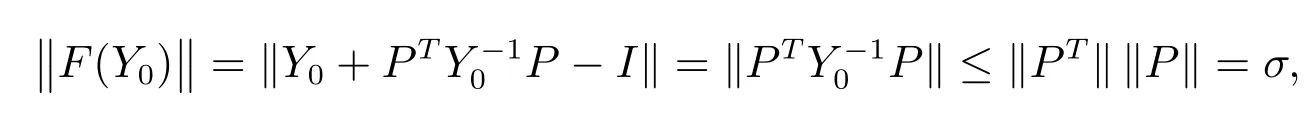
则由引理3及(4)式，有

(b)因为Y∈B(Y0,σ)，则有∥Y−Y0∥<σ．注意到∥Y0∥=1，则由引理1可得．同理有．因此，由引理2，有

(c)因为，且对任意的Y∈B(Y0,δ)，有

所以由引理1可证得

(d)由(b)式可知

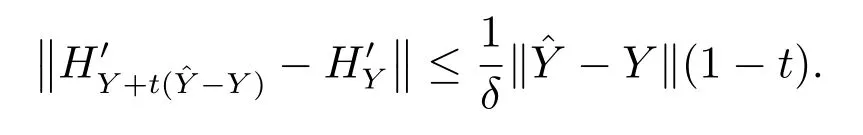
因此，有

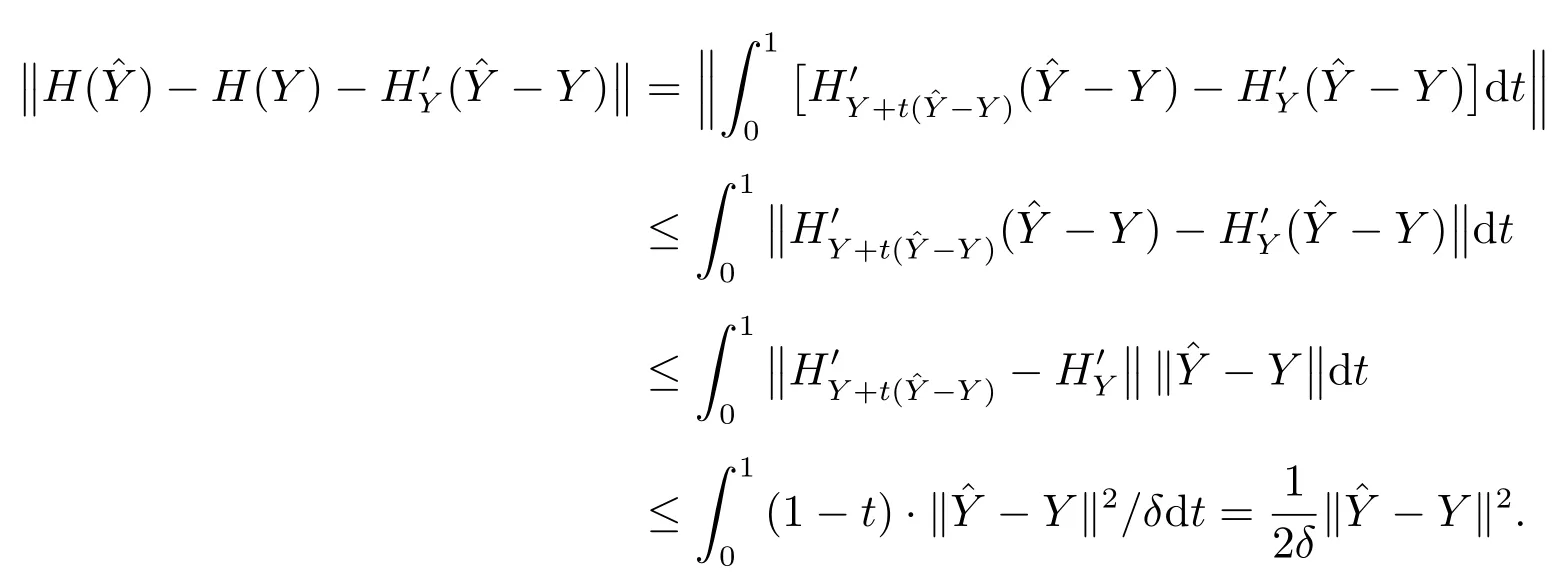
对于算法1，有如下收敛性定理．

定理1设∥P∥2=σ．若

则由算法1生成的矩阵序列收敛于F(Y)在闭球B(Y0,δ)内的唯一零点Y∗，且有．

证明 首先利用归纳法证明如下结论(e)–(h)成立：

1)当k=1时

(e)和(f)此时成立．由引理4中结论(c)，可得

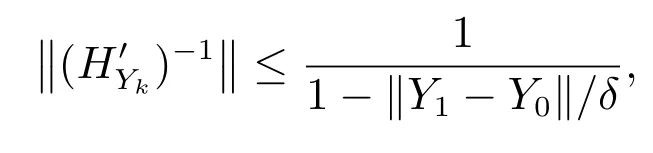
此时(g)成立．由引理4中的结论(d)，可得

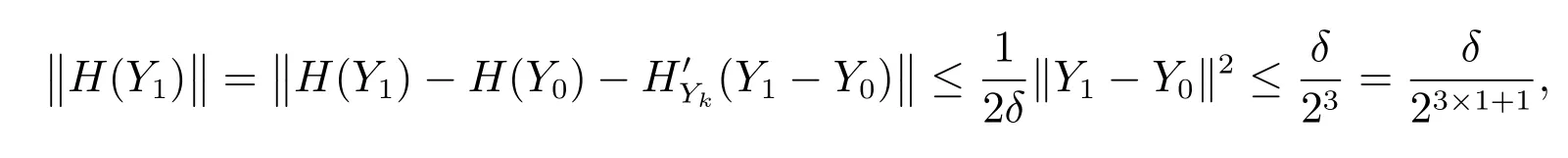
此时(h)成立．

2)假设

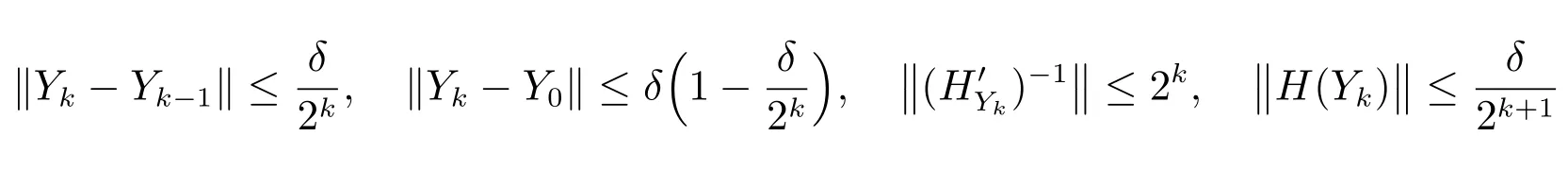
均成立，则有

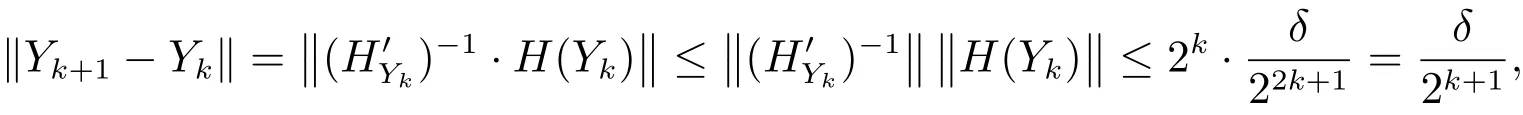
从而有

进而有

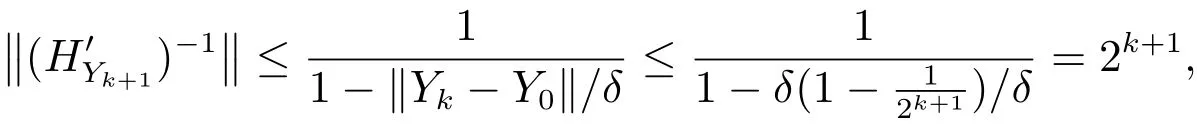
所以有

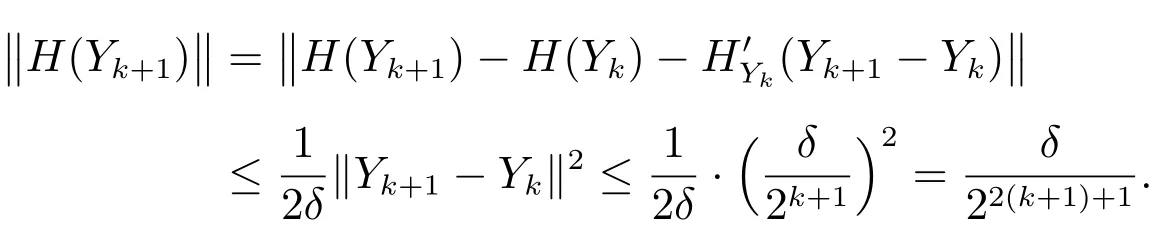
综上可知，结论(e),(f),(g),(h)均成立．

其次证明{Yk}收敛于，且,∀k>1．由(e)式，对任意的k,l≥1，有

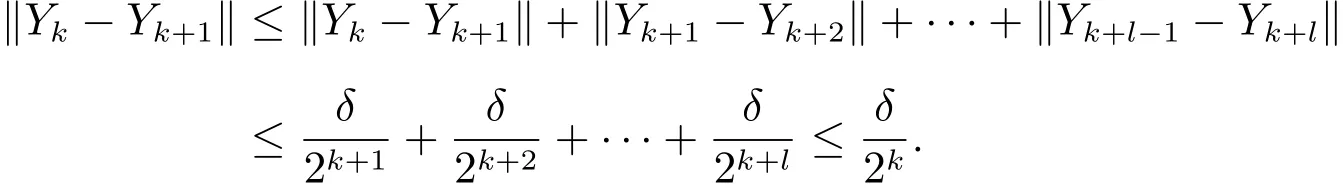
因此可知，矩阵序列{Yk}是柯西列．又由于，故存在，使得．因此，矩阵序列{Yk}收敛于Y∗．注意到

且H(Y)是关于Y的连续函数，故有

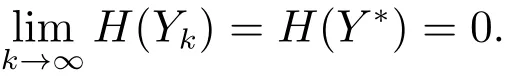
因此Y∗是F(Y)在内的零点．此外，由

可得

最后证明Y∗是F(Y)在闭球内的唯一零点．设Z∗∈B(Y0,δ)是H(Y)的零点，即H(Z∗)=0．下证,∀k≥1．

显然．

假设,∀ k=1,2,…,n成立，则

即．因此

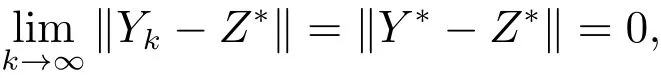
即有Y∗=Z∗，亦即Y∗是F(Y)在闭球B(Y0,δ)内的唯一零点．

综上所述，定理1得证．

注意到矩阵方程(1)和(2)的等价关系，牛顿法求解非线性矩阵方程(1)的迭代格式可以描述为如下算法．

算法2(牛顿法求矩阵方程(1)的迭代格式)

第1步给出初始矩阵X0=Q，误差容许值ε>0．令k:=0；

第2步如果ε，停止；否则，求Ek∈Rn×n，使得

其中

第3步计算Xk+1=Xk+Ek；

第4步置k=k+1，转第2步．

对于算法2，有如下收敛性定理．其证明与定理1类似，故省略．

定理2设∥(LT)−1AL−1∥2= σ．若

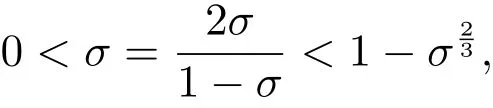
则由算法2生成的矩阵序列收敛于矩阵方程(1)在闭球B(X0,δ)内的唯一零点X∗，且有．

3 数值例子

本节将给出说明算法有效性的数值例子．对于算法2中的子问题(5)，算例中采用如下LSQRM算法[18]进行计算．

LSQRM算法(LSQR算法计算子问题(5)的近似解Ek)：

步骤1给定初始矩阵计算E0=0：

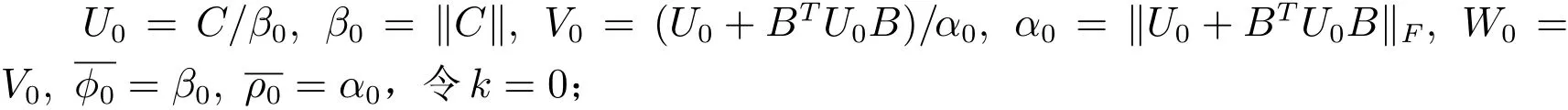
步骤2对于k=1,2,…，执行步骤2.1至步骤2.6：

步骤2.1计算

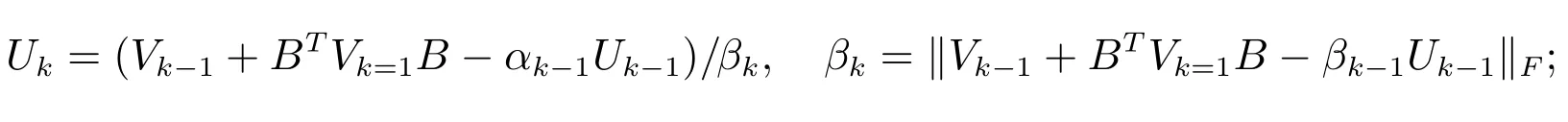
步骤2.2计算

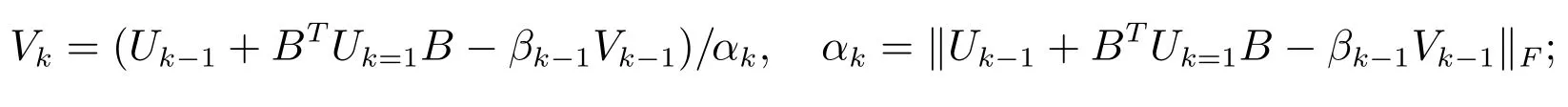
步骤2.3令

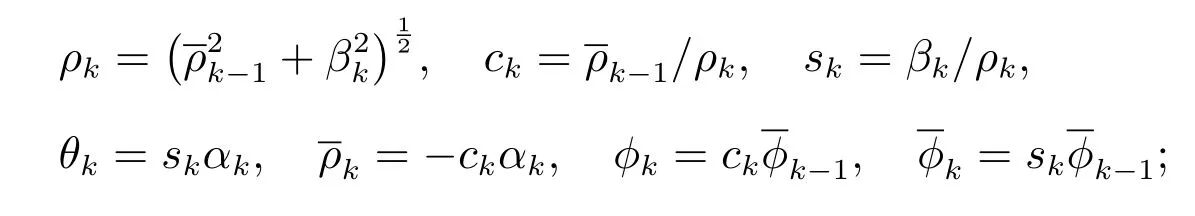
步骤2.4计算

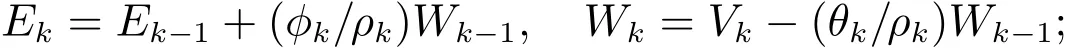
步骤2.5若ϕkαk|ck|< ε，则运行终止，Ek即为问题(6)的解；否则，转步骤2.6；

步骤2.6令k=k+1，转步骤2.1．

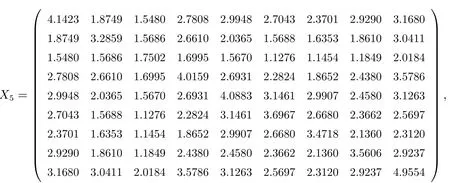
例1给定矩阵A=randn(9,9),Q=randn(9,9)(Matlab格式)如下：

则有，因此，矩阵方程(1)在闭球

内有唯一解．利用算法2迭代5步，得到矩阵方程(1)的近似解为

并且

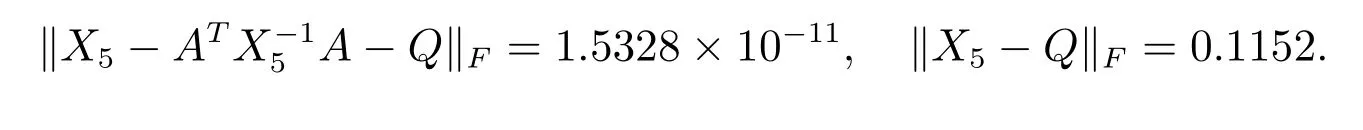
参考文献：

[1]Zhan X Z,Xie J J.On the matrix equation X+ATX−1A=I[J].Linear Algebra and its Applications,1996,247(1):337-345

[2]Ferrante A,Levy B C.Hermitian solutions of the equation X=Q+NX−1N∗[J].Linear Algebra and its Applications,1996,247(1):359-373

[3]Helton J W,Sakhnovich L A.Extremal problems of interpolation theory[J].Rocky Mountain Journal of Mathematics,2005,35(3):819-841

[4]Buzbee B L,Golub G H,Nielson C W.On direct methods for solving Poisson’s equations[J].SIAM Journal on Numerical Analysis,1970,7(4):627-656

[5]Housholder A S.The Theory of Matrices in Numerical Analysis[M].New York:Blaisdell,1964

[6]Engwerda J C.On the existence of a positive definite solution of the matrix equation X+ATX−1A=I[J].Linear Algebra and its Applications,1993,194(15):91-108

[7]Engwerda J C,Ran A M,Rijkeboer A L.Necessary and sufficient conditions for the existence of a positive definite solution of the matrix equation X+A∗X−1A=Q[J].Linear Algebra and its Applications,1993,186:255-275

[8]Meini B.Efficient computation of the extreme solutions of X+A∗X−1A=Q and X −A∗X−1A=Q[J].Mathematics of Computation,2002,71(239):1189-1204

[9]刘新国.关于求解矩阵方程X=X+AHX−1A的简单迭代[J].高等学校计算数学学报，1998,(2):163-167 Liu X G.On the simple iteration for solving matrix equation X=X+AHX−1A[J].Numerical Mathematics:A Journal of Chinese Universities,1998,(2):163-167

[10]Ramadan M A,EI-Shazly N M.On the matrix equation X+AT2m√X−1A=I[J].Applied Mathematics and Computation,2006,173(2):992-1013

[9]刘新国.关于求解矩阵方程X=X+AHX−1A的简单迭代[J].高等学校计算数学学报，1998,(2):163-167 Liu X G.On the sim p le iteration for solvingm atrix equation X=X+AHX−1A[J].Num ericalM athem atics:A Jou rnal of Chinese Universities,1998,(2):163-167

[10]Ram adan M A,EI-Shazly N M.On the m atrix equation.App lied M athem atics and Com pu tation,2006,173(2):992-1013

[11]Peng Z Y,EI-sayed S M,Zhang X L.Iterative methods for the extremal positive definite solution of the matrix equation X+AX−αA=Q[J].Journal of Computational and Applied Mathematics,2007,200(2):520-527

[12]段雪峰，廖安平.矩阵方程X+A∗X−qA=Q(q≥1)的Hermitian正定解及其扰动分析[J].高等学校计算数学学报，2008,30(3):280-288 Duan X F,Liao A P.The Hermitian positive definite solution of matrix equation X+A∗X−qA=Q(q≥1)and its perturbation analysis[J].Numerical Mathematics:A Journal of Chinese Universities,2008,30(3):280-288

[13]Liu P P,Zhang S G.Newton’s method for solving a class of nonlinear matrix equations[J].Journal of Computational and Applied Mathematics,2014,256:254-267

[14]Hasanov V I,Ivanov I G.On two perturbation estimates of the extreme solutions to the equations X±A∗X−1A=Q[J].Linear Algebra and its Applications,2006,413(1):81-92

[15]Hasanov V I.Notes on two perturbation estimates of the extreme solutions to the equations X±A∗X−1A=Q[J].Applied Mathematics and Computation,2010,216(5):1355-1362

[16]Hasanov V I,Ivanov I G,Uhlig F.Improved perturbation estimates for the matrix equations X±A∗X−1A=Q[J].Linear Algebra and its Applications,2004,379(1):113-135

[17]袁亚湘，孙文瑜.最优化理论与方法[M].北京：科学出版社，2004:7-9 Yuan Y X,Sun W Y.Optimization Theory and Methods[M].Beijing:Science Press,2004:7-9

[18]Peng Z Y.A matrix LSQR iterative method to solve matrix equation AXB=C[J].International Journal of Computer Mathematics,2010,87(8):1820-1830