Positive Period ic Solu tions of First-order Delay D ifferential Equations∗

WENG Ai-zhi

(Departm ent of Econom ics and Mnagem ent,Shanghai University of Political Science and Law,Shanghai 201701)

1 In troduction

In this paper,we study the existence of positive T-periodic solutions for the follow ing p roblem

where k∈R,p,q:[0,∞)→R are continuous and T-periodic,andτ:[0,∞)→[0,∞)is continuousw ithτ(t)≤t.In the last few years the problem of the existenceof positive periodic solutions for the delay differential equationsw ith the follow ing form

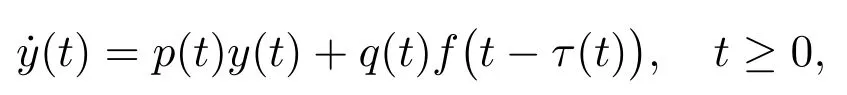
has received considerab le attention.Such equations have been proposed asmodels for a variety of physiological processes and conditions including respiration and cardiac arrhythm ias,production of blood cells.One im portant question iswhether these equations can support the existence of positive periodic solutions.This question has been studied extensively by a number of authors,for instance,in[1–5]and the references therein.The fixed point theorem in cones has been mostly used to prove the existence of solutions of this type of equations.In the literature,the existence of positive solutions for equations of the above type ismainly proved based on the assum ption that the functions p(t)and q(t)are T-periodic and satisfy the conditions

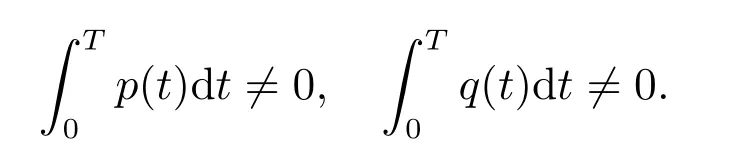
Recently,paper[6]shows the existence of positive periodic solutions of equation(1)when k=1,while they do not satisfy the above two conditions.

Wew ill use the follow ing Schauder’s fixed point theorem to prove themain results in the next section.

Lemm a 1[7]LetΩbe a closed,convex and nonem p ty subset of a Banach space X.LetΓ:Ω→Ωbe a comp letely continuousmapping.Then there exists at least an x∗such thatΓx∗=x∗.

2 Main result

Theorem 1Suppose that there is a T-periodic function w ∈ C([0,∞),(0,∞))such that

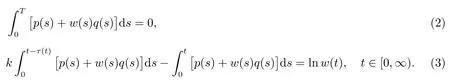
Then there exists a positive T-periodic solution of(1).

ProofLet Y be the space of continuous functions y:[0,∞)→R w ith the supremum norm.With regard to the equality(2),we define

wherewe have taken into account that p(t)+w(t)q(t)is continuous and T-periodic.

The closed,bounded and convexΩ⊂Y is defined by

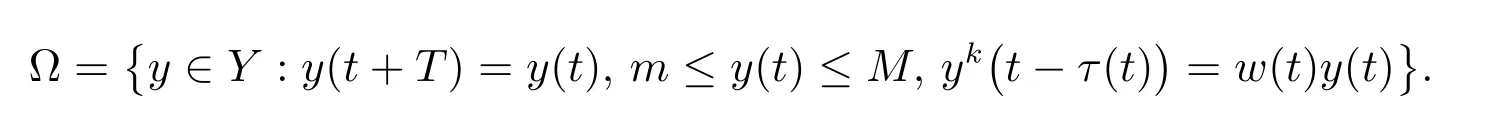
InΩwe define the operator

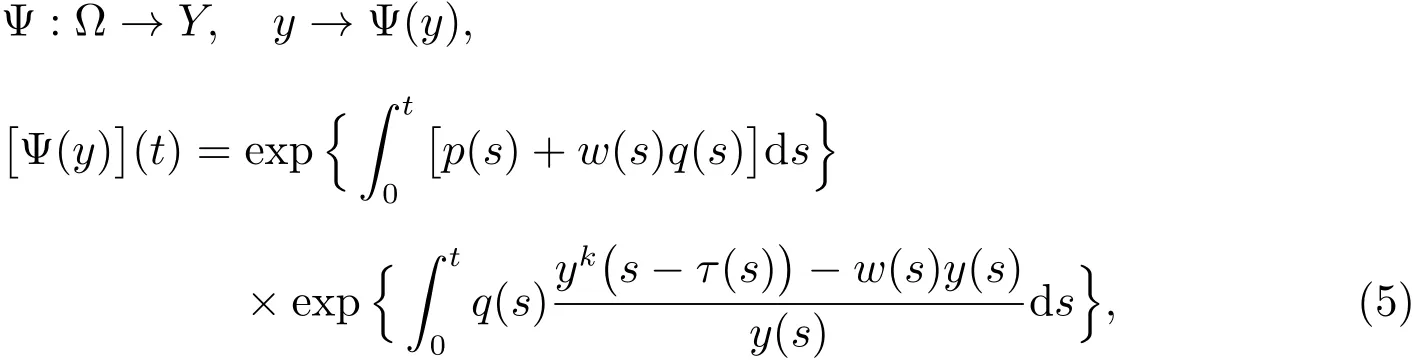
for t∈ [0,∞).

It is easy to prove that y is a positive periodic solution of(1)if and only if it is a fixed point ofΨ inΩ.In order to obtain the existence of a fixed point forΨ by using Lemma 1,we first prove thatΨ mapsΩ intoΩ.For every t≥0,y∈Ω,we have

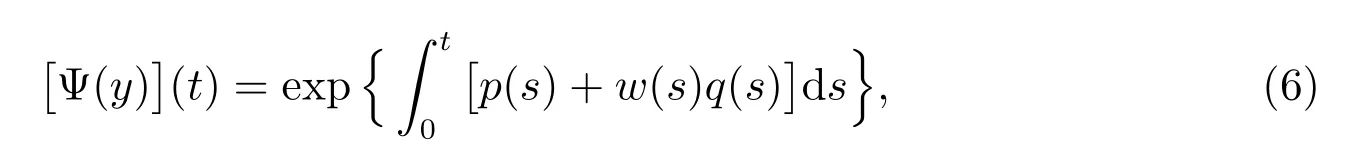
and then,by using(4)we obtain

By using(3)and(6)we obtain

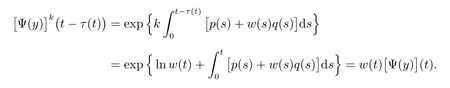
A straight calculation yields[Ψ(y)](t+T)=[Ψ(y)](t)since(2)holds.

Next,we proveΨis com pletely continuous.Indeed,Ψis trivially continuous and

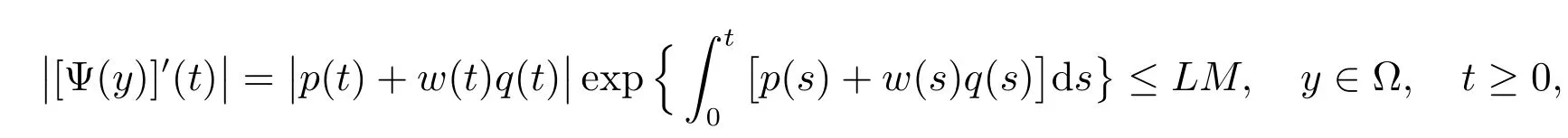
where L satisfies|p(t)+w(t)q(t)|≤L.The proof thatΨis com pletely continuous is then com pleted.Based on Lemma 1Ψhas a fixed point y∈Ωsuch that

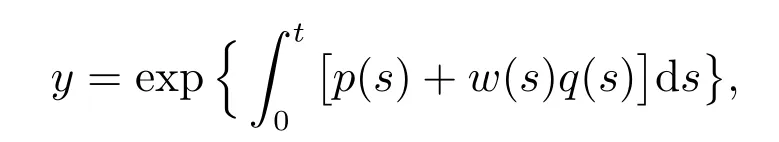
and consequently y is a solution of(1).

The follow ing corollary is obtained as the particular case of Theorem 1.The corollary is themain Theorem 2.1 in[6].Taking k=1,equation(1)is

Corollary 1Suppose that there is a T-periodic function w ∈ C([0,∞),(0,∞))such that(2)holds and

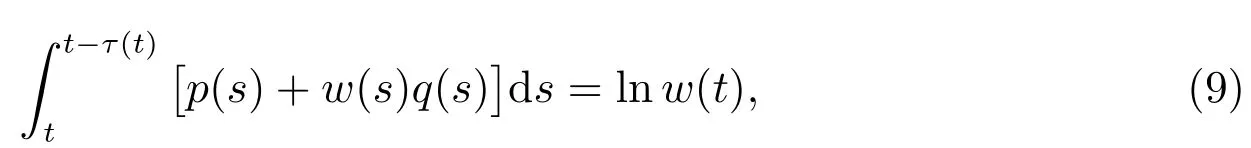
for every t∈ [0,∞).Then there exists a positive T-periodic solution of equation(8).

ProofThe condition(9)is exactly the condition(3)by taking k=1.

3 Examples

Example 1Consider the delay differential equation

To prove the validity of the hypotheses(2)and(3),we let w(t)=e−4sintand obtain

and

where

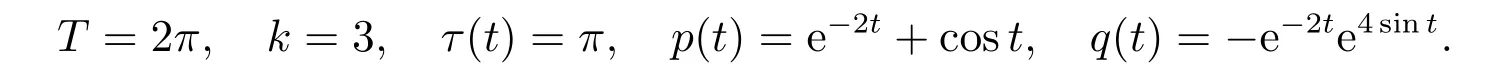
By Theorem 1,(10)has a positive 2πsolution

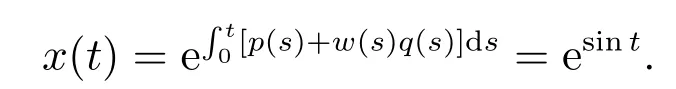
Example 2Consider the delay differential equation

where the periodic.There exists asuch that p(t)+w(t)q(t)=3 cos3t.The hypotheses(2)and(3)are valid,since

Then(11)has a positive 2πsolution

References:

[1]Wang H Y.Positive periodic solutions of functional differential equations[J].Journal of Differential Equations,2004,202(2):354-366

[2]Chen R P,Ma R Y,He Z Q.Positive periodic solutions of first-order singular systems[J].Applied Mathematics and Computation,2012,218(23):11421-11428

[3]Wang H Y.Positive periodic solutions of singular systems of first order ordinary differential equations[J].Applied Mathematics and Computation,2011,218(5):1605-1610

[4]Weng A Z,Sun J T.Impulsive stabilization of second-order nonlinear delay differential systems[J].Applied Mathematics and Computation,2009,214(1):95-101

[5]Weng A Z,Sun J T.Positive periodic solutions of first-order functional differential equations with parameter[J].Journal of Computational and Applied Mathematics,2009,229(1):327-332

[6]Rudolf O.Positive periodic solutions of delay differential equations[J].Applied Mathematics Letters,2013,26(12):1141-1145

[7]Shi B,Zhang D C,Gai J M.Theory and Applications of Differential Equations[M].Beijing:National Defense Industry Press,2005