粘弹流动的间断有限元模拟∗

郭虹平,欧阳洁,杨广辉,周 文

(西北工业大学应用数学系，西安 710129)

1 引言

近年来，随着聚合物工业的飞速发展，粘弹流体流动的数值研究备受关注．粘弹流体流动的控制方程由质量方程、动量方程和本构方程构成，属于椭圆-双曲混合型偏微分方程组．数值模拟算法的不准确可能会导致应力张量正定性的改变，尽管此变化对椭圆型方程的求解影响不大，但对双曲型方程的求解会带来很大误差[1]．因此，发展适合求解椭圆-双曲混合型偏微分方程组的高精度方法很有必要．

目前模拟粘弹流动的主要方法是有限差分法、有限体积法和有限元法．有限差分法求解规则区域的问题时，算法实施容易，但对复杂区域的适应性很差．有限体积法有很好的几何灵活性，逼近及格式都是局部的，但不能在一般非结构网格上取得高精度．传统有限元法对不规则区域的适应性较好、精度较高，但不适于处理间断问题，对网格加密或减疏处理时需考虑连续性的限制．间断有限元(discontinuous Galerkin，简称DG)法兼顾有限体积法及有限元法的优点，采用局部逼近，精度高且高度并行，易于处理非规则区域[2]．

Yurun[3]分别采用加入稳定化方案的传统有限元法和DG方法求解稳态UCM本构模型，验证了两种方法均可有效求解光滑问题．但对含应力奇异点的平板收缩流模拟时，DG方法表现出更好的鲁棒性．2005年，Kim等人[4]模拟了基于Oldroyd-B本构模型描述的粘弹流动，实现了质量方程、动量方程和本构方程的耦合求解．其质量方程和动量方程的求解采用传统有限元法，本构方程的求解采用DG方法，且用并行算法提高了计算效率．但是，运用非结构网格上统一的DG方法对粘弹流动进行模拟研究却鲜有报道．

鉴于Oldroyd-B本构模型是检验数值算法优劣的最苛刻的粘弹本构模型，而发展基于非结构网格的数值方法是模拟复杂区域上实际问题最有效的技术手段，本文基于非结构网格，建立了Oldroyd-B粘弹流动的统一DG求解框架．该框架包含采用IPDG(interior penalty DG)求解质量方程和动量方程，RKDG(Runge-Kutta DG)求解本构方程这两个核心．对平面Poiseuille流和4:1平板收缩流问题的数值模拟，验证了本文方法的有效性．

2 粘弹流动的控制方程

考虑由Oldroyd-B[5,6]本构模型描述的瞬态、不可压、等温流动问题，其流场控制方程如下：

质量方程

动量方程

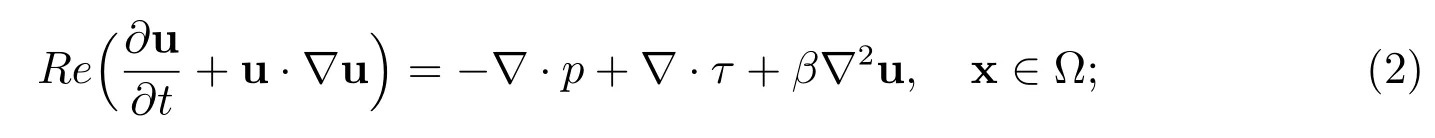
本构方程

其中u为流体速度，p为压力，τ为应力张量；表示牛顿粘度ηs和总粘度η0的比；，ρ为密度，U为特征速度，L为特征长度；，λ为特征松弛时间；为τ的上随体导数，即

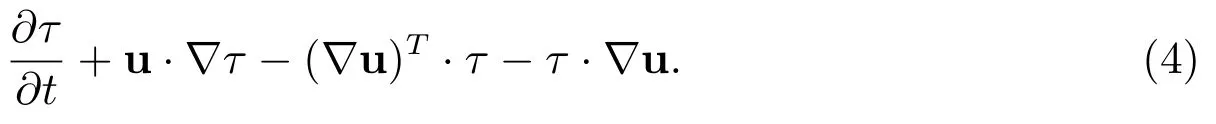
为便于构造求解格式，化简(3)式，得

其中

3 本构方程的RKDG方法求解

Cockburn和Shu提出了求解双曲型方程的RKDG方法[7-9]．Hesthaven和Warburton[10]则通过巧妙合理地布置节点来构造基函数，简化了DG方法在非结构网格上的实施．本文将基于非结构网格，用RKDG方法单独求解Oldroyd-B本构方程，以获得新的时间层的应力张量．

为构造本构方程的RKDG方法，结合(1)式和(5)式可得

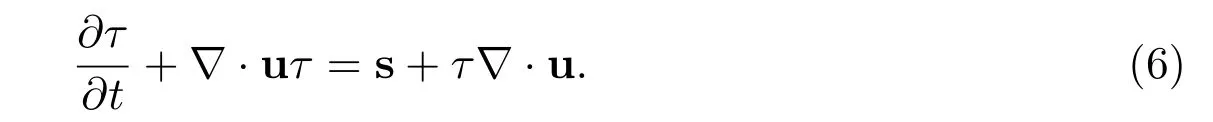
令f(τ)=uτ，则不可压缩流场中Oldroyd-B本构方程的守恒形式可表示成

为求解(7)式，对区域Ω构造三角剖分Th，其中剖分单元用Ωk表示，并定义有限元空间

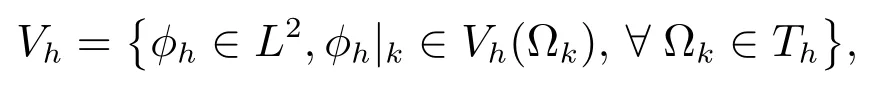
Vh(Ωk)是单元Ωk上的基函数，其中np为基函数的个数．本文取Lagrange型基函数lki(x)，其系数便是相应节点处物理量的值．

设单元Ωk上的逼近函数形式为

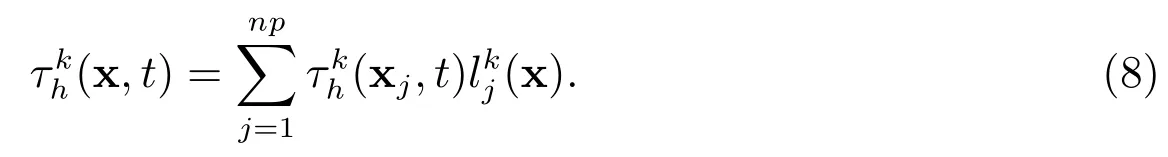
对(7)式两边乘以试验函数，且进行一次分部积分，得DG方法的弱形式为

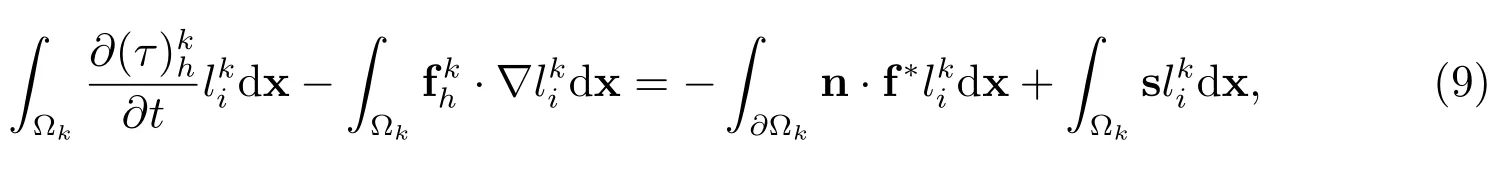
其中f∗=uτ∗为数值通量[11]，n为单元Ωk边界上的外法向向量．为保证数值格式的稳定性，τ∗选用迎风型数值通量，见图1，即

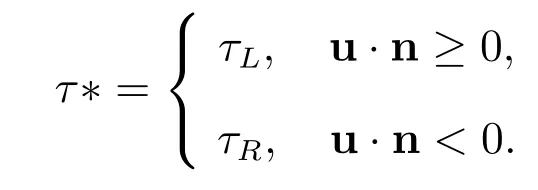
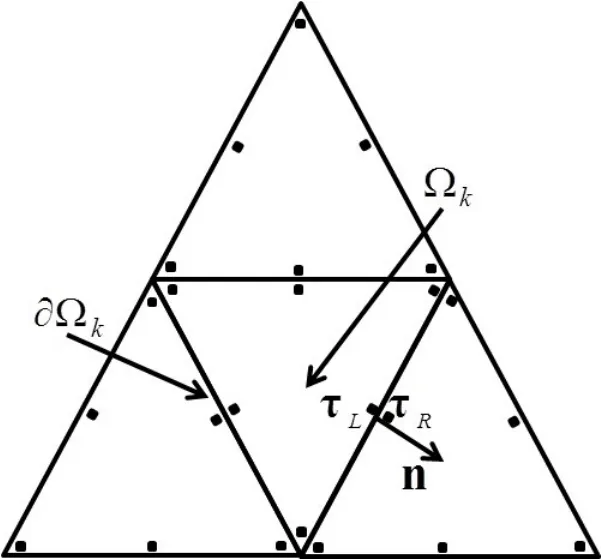
图1:二维迎风通量示意图

由(8)式知，在单元Ωk上

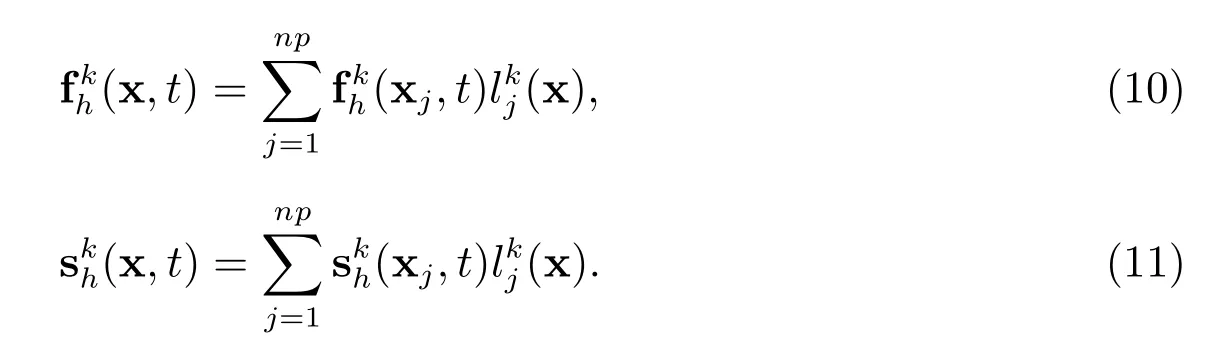
将(8),(10),(11)式代入(9)式，可得

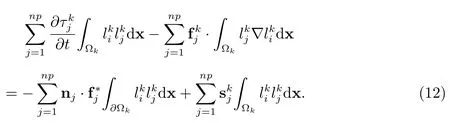
定义如下矩阵：质量矩阵

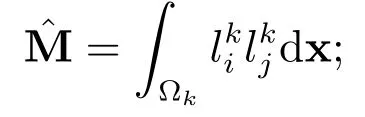
刚度矩阵

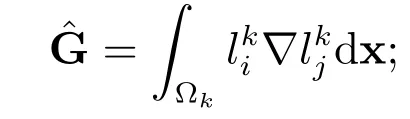
边界矩阵

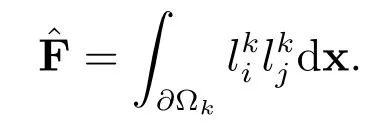
化简(12)式，可得如下常微分方程

其中

采用TVD Runge-Kutta方法对(13)式进行显式时间离散[11]即为RKDG方法，本文采用二阶RK格式．

4 质量方程和动量方程的IPDG求解

4.1节和4.2节将分别给出求解质量方程、动量方程的时间分裂格式和空间离散格式(即IPDG方法)．其中动量方程(2)中的应力作为拟体力处理，且在动量方程、质量方程的求解过程中不断地更新速度和压力．

4.1 时间分裂格式

为求解动量方程(2)，采用刚性稳定的时间步长法[12]，将第n层到第n+1层每个时间步的推进分为三个阶段．

步骤1非线性对流方程

步骤2压力方程

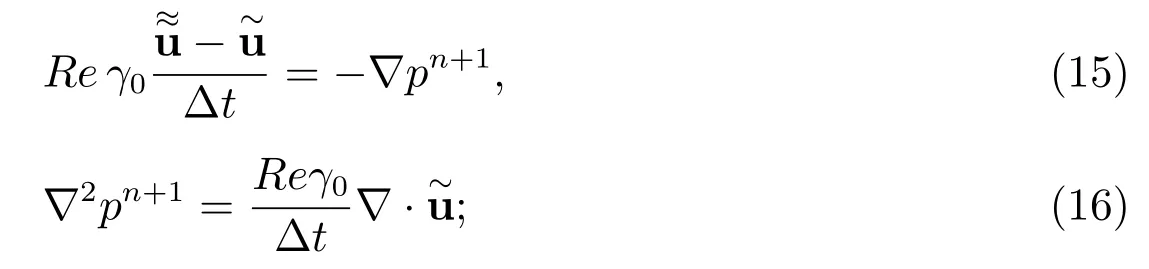
步骤3粘性方程

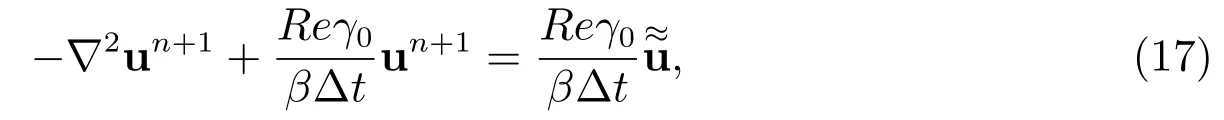
其中n=0时，计算参数取为

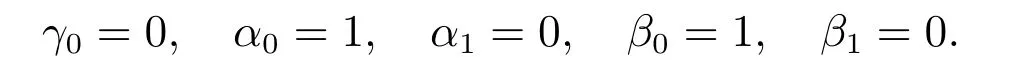
以后的参数为

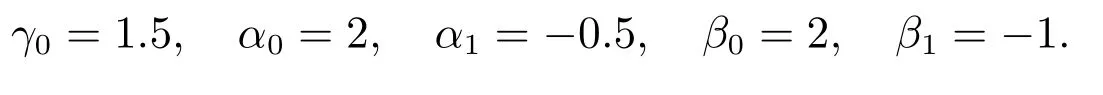
由分裂过程可知，第1步通过求解对流方程(14)式来计算预估速度；第2步引入中间速度完成压力投影，通过求解压力Poisson方程(16)式得到压力；第3步通过(15)式更新中间速度，最后隐式求解粘性方程(17)式得到un+1．

4.2 空间离散

下面给出分裂方程(14),(16),(17)的空间离散格式．其中非线性对流方程(14)的DG方法求解中，选用合适的数值通量以提高数值解的稳定性；椭圆方程(16)和(17)的DG方法求解中，选用单元计算模板较小的IPDG方法[13]．

为下文推导方便，定义为u的跳跃，为u的平均．选用Lax-Friedrichs通量对方程(14)的右端项进行空间离散，得

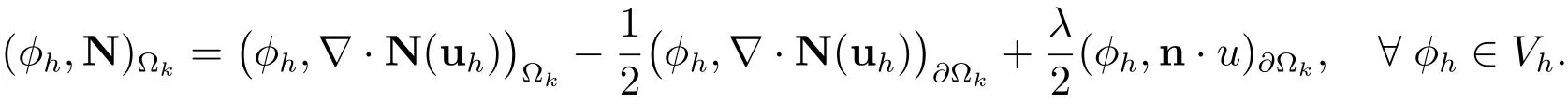
椭圆型方程(16)和(17)分别为Poisson和Helmholtz方程，其统一形式为

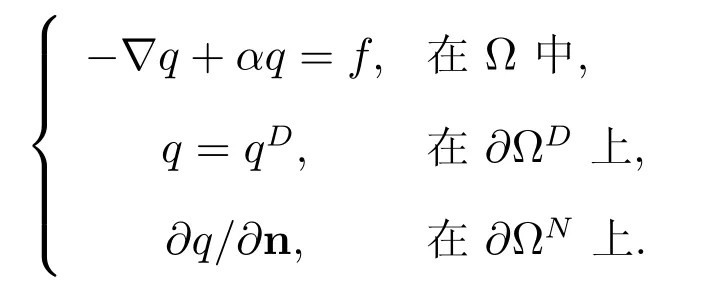
对于Possion方程：；对于Helmholtz方程：

选用IPDG方法可得上述椭圆方程的离散结果为

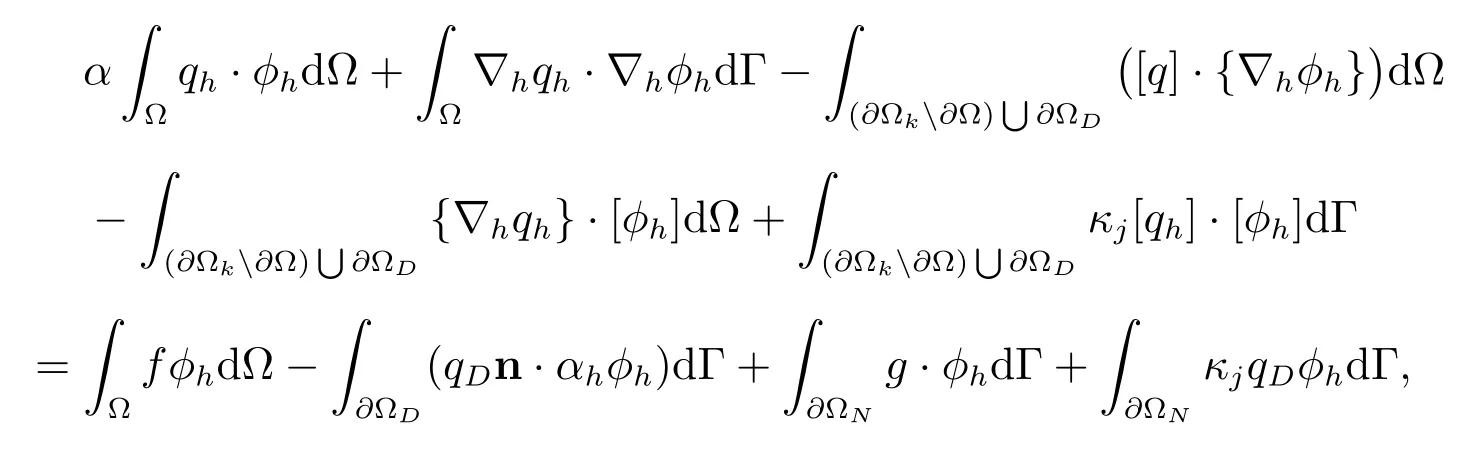
其中∂ΩD和∂ΩN分别为Dirich let和Neumann边界条件，Γ为Γh中的所有单元边界的集合，κj为惩罚因子，与网格尺寸同阶．

5 统一的DG算法

统一算法的宗旨是将属于椭圆-双曲混合型偏微分方程组的粘弹流动控制方程采用相同的数值方法进行统一求解，从而使方程之间的数据信息传递简单而且快捷，使其程序实现统一化．本文建立的统一DG框架包含两个核心：一是采用IPDG方法结合Asam s-Bashforth二阶时间离散格式求解质量方程和动量方程；二是采用RKDG方法求解本构方程．这三套方程的耦合即构成了本文粘弹流动模拟的统一DG方法．其算法流程如下：

步骤1初始化速度u0、压力p0和应力τ0；

步骤2对于i=0,…,N(t0→tN):

1)将应力τi作为拟体力，引入中间速度,，运用第4节的离散格式求解质量方程和动量方程，更新速度、压力；

2)根据更新的速度ui+1，更新si+1；

3)运用第3节的RKDG方法求解本构方程，更新应力场；

步骤3输出数据．

6 数值算例

6.1 平面Poiseuille流

当Re很小时，平面Poiseuille流具有解析解，可以定量检验数值算法的稳定性和精度．图2给出了平面Poiseuille流的流动示意．流场在出口处充分发展，固壁处采用无滑移边界条件．入口速度设为u=0.4y(1−y),v=0．

图2:平面Poiseuille流动示意

Oldroyd-B模型的稳态Poiseuille流动的精确解为[14]：

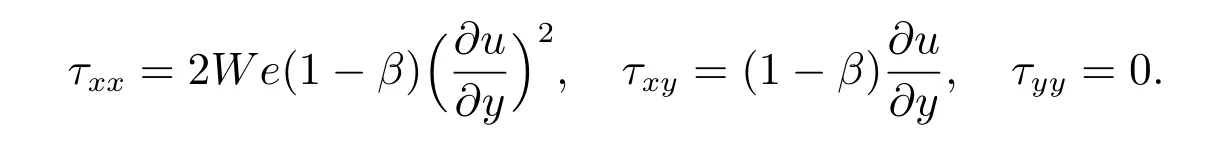
图3给出了不同We数下第一法向应力和剪切应力在x=4时的数值解与解析解比较．图3(a)中各曲线从上到下依次表示Re=0.01,,We=1,We=2,We=3,We=4,We=5,We=6时第一法向应力的数值解和解析解，图3(b)为We=2时的剪切应力模拟结果．可以看出，第一法向应力和剪切应力的数值解和解析解吻合很好，并且在We=6时仍可得到满意结果．表1给出了应力τxx在l2范数下的误差分析．由表1可知该方法具较高的计算精度，且随着网格的加密和插值次数的提高，模拟结果更加精确．

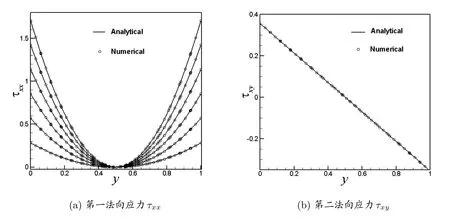
图3: 平面Poiseuille流数值解与解析解的比较

表1: 应力τxx在l2范数下的误差分析

6.2 平板收缩流

4:1平板收缩流具有旋转、拉伸和强剪切等复杂的流动特征，在收缩口处存在应力奇点，其数值解存在大梯度变化．对4:1粘弹收缩流动问题的模拟，可以进一步验证算法对模拟非线性复杂粘弹流动的有效性．

图4给出了4:1平板收缩流的计算区域、边界条件及网格剖分．计算时固壁处速度采用无滑移边界条件，入口处设为

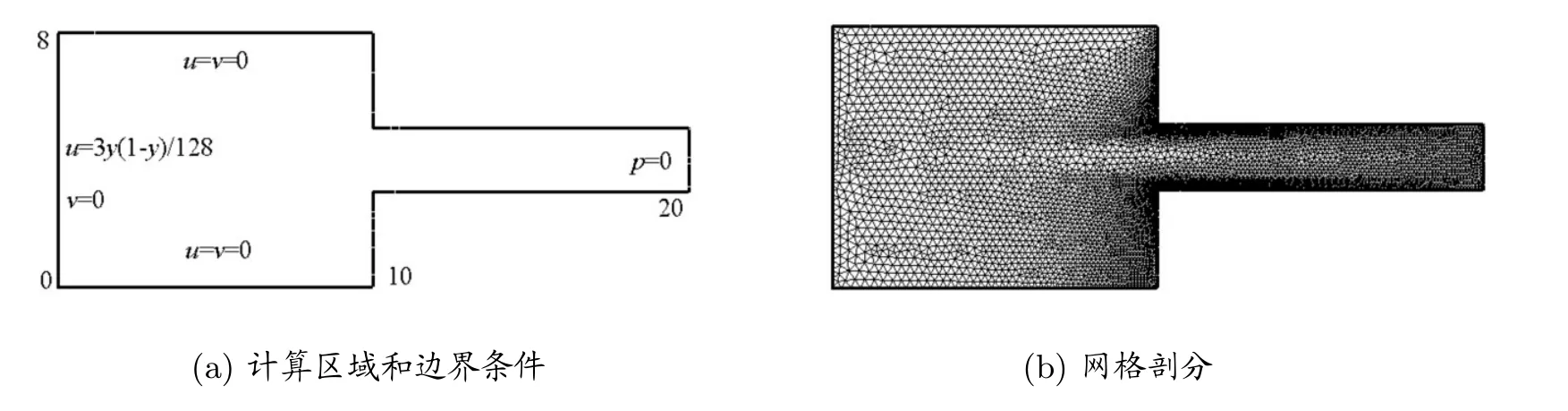
图4:平板收缩流示意

为检验本构模型求解的正确性，首先考察忽略非线性项影响即(N(un)=0)的蠕动流动．图5给出了Re=1时，在不同We数下收缩口附近蠕动流的流线分布．从图中可以看出随着We数的增大，流场中的涡流区域逐渐减小，这与文献[15]的数值结果一致．

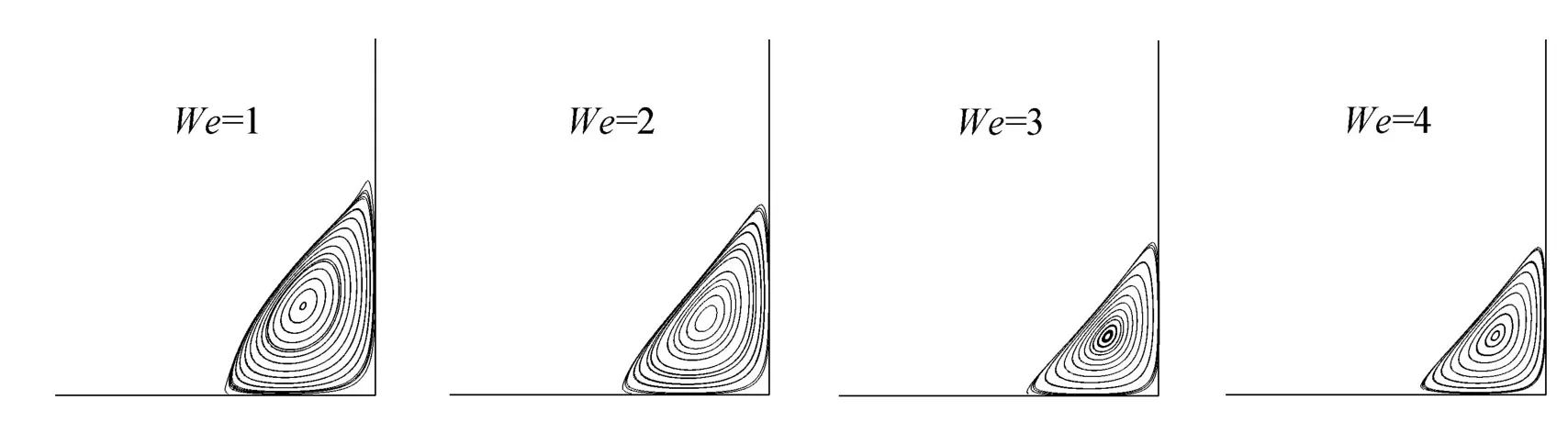
图5: 蠕动流在不同We数下的流线比较

为真正模拟Oldroyd-B本构模型的粘弹流体流动，其次考虑具有非线性项影响的粘弹流动．图6至图9给出了在Re=1,We=1时收缩口附近粘弹流动的流线分布和应力分布．从图中可以看出，收缩口附近形成强拉伸区域，在上游的拐角处，流动以旋转为主，形成主涡，这与文献[1,16]预测的流动趋势完全吻合．

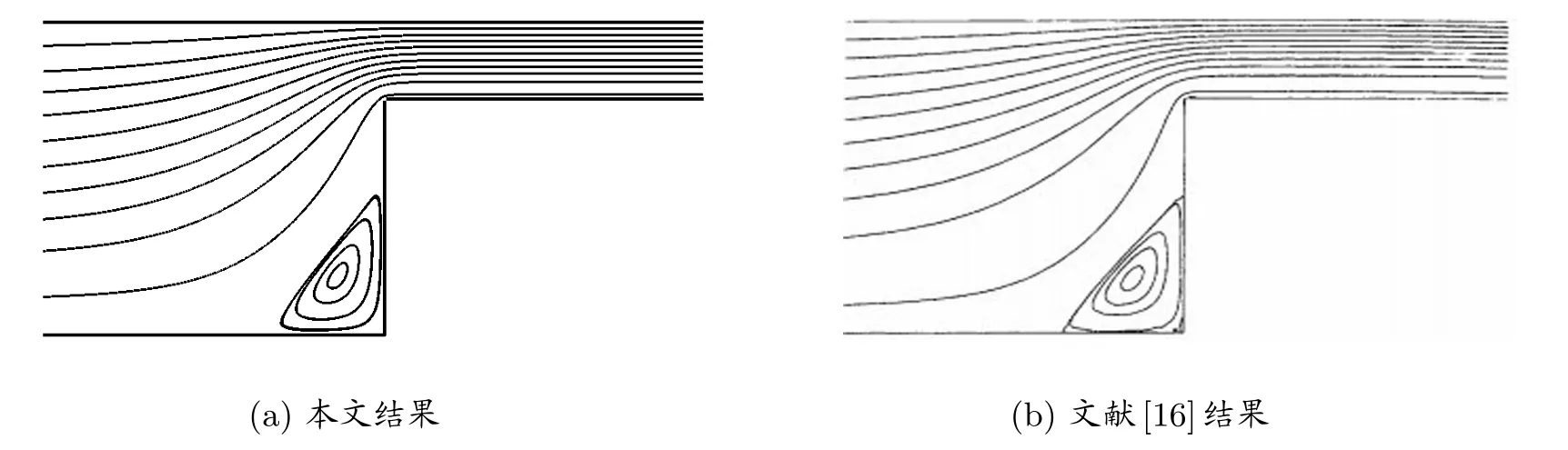
图6:收缩口附近的流线分布

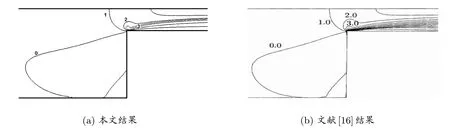
图7: 收缩口附近的应力τxx分布

图8: 收缩口附近应力τxy分布

图9: 收缩口附近的应力τyy分布

7 结论

本文建立了一种求解Oldroyd-B粘弹流体流动的数值方法，给出了粘弹流动求解的统一DG框架．该方法运用IPDG求解质量方程和动量方程，运用RKDG求解本构方程，成功实现了粘弹流动流场控制方程的DG方法耦合求解．对平面Poiseuille流和4:1平板收缩流问题的数值模拟结果表明：

1)本文方法在求解Oldroyd-B本构模型时无需加入稳定化方案，其实施比传统有限元方法更为简便；

2)采用统一DG框架求解流场控制方程是模拟非牛顿流动问题的一种有效方法．该方法使得三套方程之间的数据信息传递简单而且快捷，其程序实现易于统一化；

3)平面Poiseuille流模拟的计算结果与精确解吻合很好，从而说明该方法具有很好的稳定性和较高的计算精度．与文献吻合的平板收缩流模拟结果进一步说明本文的统一DG方法可以在非结构网格上模拟包含应力奇异点的复杂粘弹流动问题；

4)本文的统一DG方法的实施并不局限于Oldroyd-B本构模型，也可推广到其它微分型本构方程的求解．并且，该方法不依赖于问题的维数，故也可方便地扩展到高维问题的求解．

参考文献：

[1]赵晓凯，欧阳洁，李五明.平板收缩流的对数构象模拟[J].工程数学学报，2012,29(5):703-714 Zhao X K,Ouyang J,Li W M.Numerical simulation of planar contraction flow using log-conformation tensor approach[J].Chinese Journal of Engineering Mathematics,2012,29(5):703-714

[2]Cheng J,Shu C W.High order schemes for CFD:a review[J].Chinese Journal of Computational Physics,2009,26(3):633-655

[3]Yurun F.A comparative study of the discontinuous Galerkin and continuous SUPG finite element methods for computation of viscoelastic flows[J].Computer Methods in Applied Mechanics and Engineering,1997,141(1):47-65

[4]Kim J M,Kim C,Kim J H,et al.High-resolution finite element simulation of 4:1 planar contraction flow of viscoelastic fluid[J].Journal of Non-Newtonian Fluid Mechanics,2005,129(1):23-37

[5]Bird R B,Armstrong R C,Hassager O.Dynamics of polymeric liquids[J].Fluid Mechanics,1987,95(1):310-349

[6]Na Y,Yoo J Y.A finite volume technique to simulate the flow of a viscoelastic fluid[J].Computational Mechanics,1991,8(1):43-55

[7]Cockburn B,Shu C W.The Runge-Kutta local projection p1-discontinuous Galerkin finite element method for scalar conservation laws[J].Journal of Numerical Analysis,1991,25(3):337-361

[8]Cockburn B,Shu C W.TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws II:general framework[J].Mathematics of Computation,1989,52(186):411-435

[9]Cockburn B,Shu C W.The Runge-Kutta discontinuous Galerkin method for conservation laws V:multidimensional systems[J].Journal of Computational Physics,1998,141(2):199-224

[10]Hesthaven J S,Warburton T.Nodal Discontinuous Galerkin Methods:Algorithms,Analysis,and Applications[M].New York:Springer,2008

[11]Shu C W.Runge-Kutta discontinuous Galerkin methods for convection-dominated problems[J].Journal of Scientific Computing,2001,16(3):173-261

[12]Karniadakis G E,Israeli M,Orszag S A.High-order splitting methods for the incompressible Navier-Stokes equations[J].Journal of Computational Physics,1991,97(2):414-443

[13]Arnold D N,Brezzi F,Cockburn B,et al.Unified analysis of discontinuous Galerkin methods for elliptic problems[J].SIAM Journal on Numerical Analysis,2002,39(5):1749-1779

[14]Baaijens FPT.Mixed finite element methods for viscoelastic flow analysis:a review[J].Journal of Non-Newtonian Fluid Mechanics,1998,79(2-3):361-385

[15]Phillips T N,Williams A J.Comparison of creeping and inertial flow of an Oldroyd-B fluid through planar and axisymmetric contractions[J].Journal of Non-Newtonian Fluid Mechanics,2002,108(1):25-47

[16]Aboubacar M,Webster M F.A cell-vertex finite volume/element method on triangles for abrupt contraction viscoelastic flows[J].Journal of Non-Newtonian Fluid Mechanics,2001,98(s2-3):83-106