维修服务契约的最优设计和分析∗
彭 懿,吴锦标
(1-长沙师范学院初等教育系,长沙 410100;2-中南大学数学与统计学院,长沙 410083)
1 引言
在市场激烈竞争的今天,随着消费者维权意识的提高和消费观念的变化,消费者在选购产品时,不仅注意到产品实体本身,在同类产品的质量和性能相似的情况下,更加重视产品的售后服务.因此,企业在提供价廉物美的产品的同时,向消费者提供完善的售后服务,已成为现代企业市场竞争的新焦点.售后服务包括维修、安装升级、设备调整、提供技术支持、咨询和培训,以及提供融资服务,甚至于文化活动等等,内容十分广泛.本文尝试利用数学方法定量地分析、优化和设计售后服务中的维修服务契约.
Murthy和Padmanabhan[1]最先将服务契约当做一种广义的保修行为来研究机器维修模型.Murthy和Ashgarizadeh[2]首先利用博弈论研究了一台机器和一个修理工的维修服务契约模型.他们利用Stakelberg博弈公式得到了代理商的最优决策结构.而后,Ashgarizadeh和Murthy[3]将此模型推广到多台机器和单个修理工情形.但他们都没有考虑机器的保修期和保修费等.Yeh和Lo[4]研究了对于可修产品的预防–维修策略.Pascual和Ortega[5]通过建立一个随机模型确定了产品每次检测和大修的最优时间.关于研究维修服务契约模型的主要方法和结果,读者可参见Murthy和Blischke[6]的综述以及Murthy和Djamaludin[7]的文献评述和Murthy和Blischke[8]的著作.近年来,Huber和Spinler[9]对维修服务合约进行了最优定价分析.Xiang等[10]考虑了一个在马尔可夫随机环境中运行的维修系统的最优维修策略.本文推广了Ashgarizadeh和M urthy[3]的工作,利用多服务器排队理论和博弈理论对具有多台机器和多个修理工的机器维修服务合约进行最优设计,得到了最优保修期、保修费和修理工数目.
2 模型描述
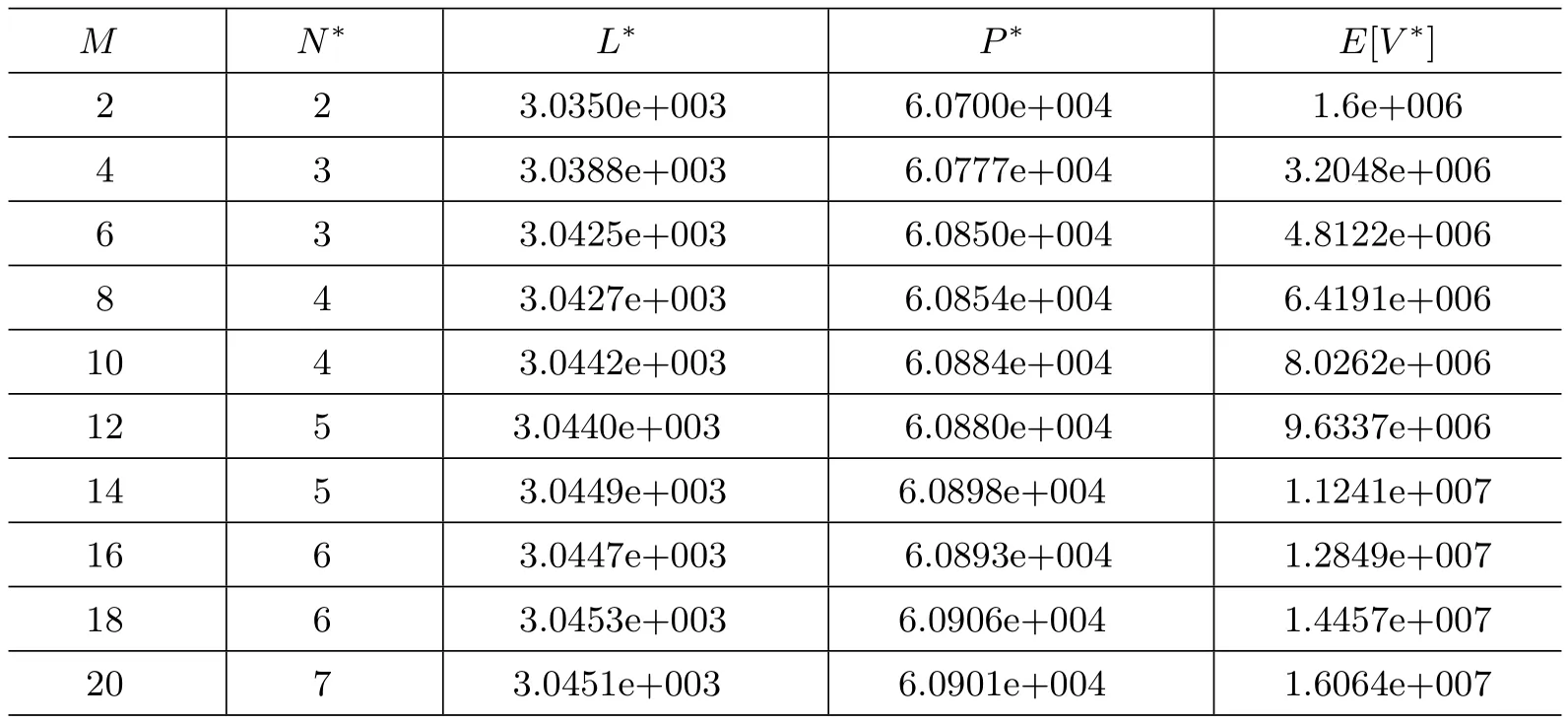
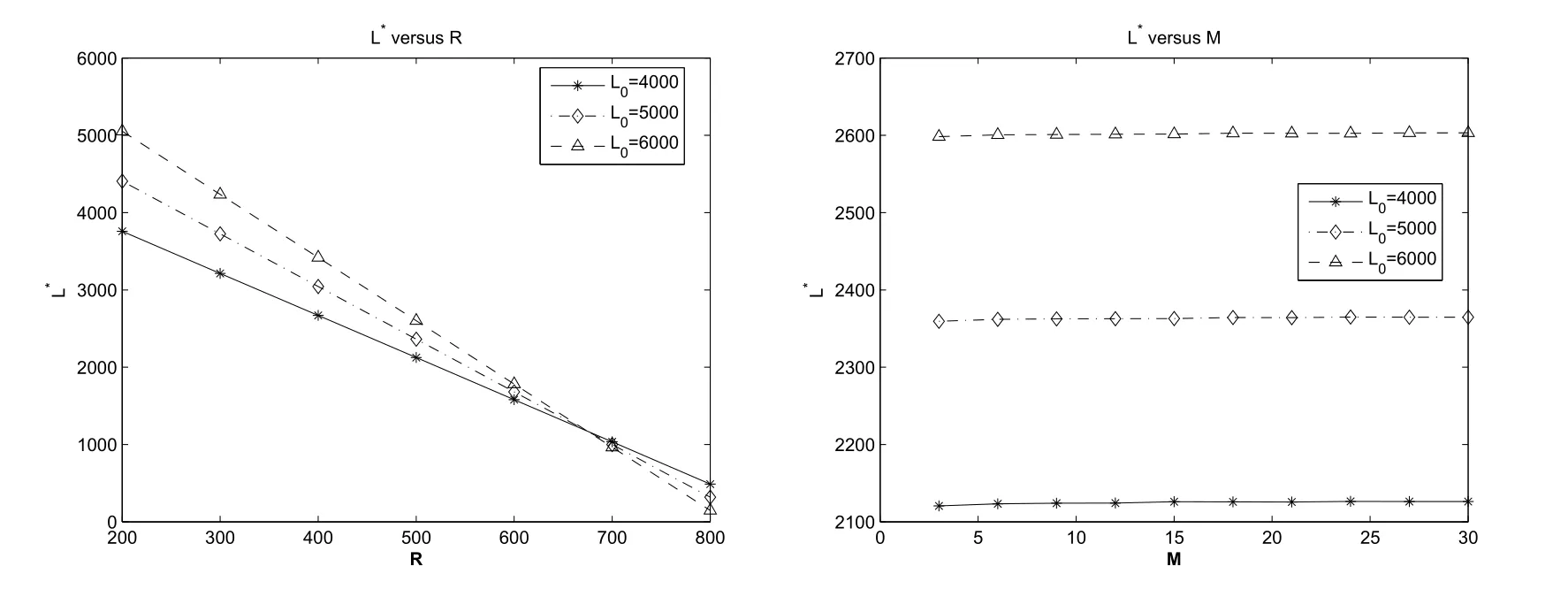
假设某公司以单位价格Cp,从一设备制造商(代理商)购入M台使用年限(寿命)为L0的机器.每台机器正常运转时每单位时间可产生收益R,而机器发生故障时则不会产生收益.假设这M台机器相互独立地工作,每台机器相继发生故障的间隔时间服从参数为λ的指数分布.机器一旦发生故障,马上送往售后服务部门进行维修,修复后立即投入使用.假设有N(1≤N≤M)个修理工,代理商付给每个修理工的固定费用为Cn.维修规则为机器先故障先维修,每台发生故障的机器的修理时间χ服从参数为µ的指数分布.代理商制定了如下维修服务契约:对每台保修期为L(0≤L≤L0)的机器,购买者一次性交纳保修费P(L),这里假设函数P(L)单调增、凸且在区间[0,L0]内二次可微.若在保修时期内送往维修的机器没有在规定的时间T内修好,则给予一定的补偿.令随机变量τ表示发生故障的机器送往维修直到修好的这段时间.若τ>T,则补偿费用为δ(τ−T),若τ≤T,则不补偿.若在保修期外发生故障的机器,则每次维修需支付Cs的维修费且无任何补偿.假设每台发生故障的机器的一次维修成本费为Cr(Cr 对机器j(j=1,2,…,M),我们令其在时间区间[0,L)内发生故障的次数为Xj,在时间区间[L,L0)内发生故障的次数为Yj.再令Wji为机器j发生第i次故障时送往维修直到修好的这段时间.显然,Wji等于其等待修理时间和修理时间之和.令Uj为第j台机器产生的纯收益,V为代理商的总收益,则我们有 注意到此维修服务模型等价于有限源M/M/N排队系统,其服务规则为先到先服务(FCFS).顾客到达率为 服务率为 定理1令N(t)表示时刻t发生故障在维修部门等待修理和正在修理总的机器数目,设 则 其中 证明 机器发生故障被送往修理这个过程可看做是一顾客有限源的M/M/N排队系统.从而由经典的排队论易得上述结论. 推论1令H和Hq分别表示在稳态下发生故障的机器数与等待修理的机器数,则有 记Wq为顾客有限源的M/M/N排队系统中顾客的等待时间(不包括服务时间),则Wji=Wq+χ. 定理2稳态下,故障机器的等待修理时间分布函数Wq(t)=P{Wq≤t}为 证明 参见G ross和Harris[11]著的《排队论基础》. 由于Wq与χ相互独立,于是Wji的分布函数为 注1推导上述公式利用了如下等式 推论2发生故障的机器从被送去修理到修好正常运作的平均时间为 推论3维修一台发生故障的机器的平均补偿费用为 利用推论2和推论3,我们便可得到如下定理. 定理3每台机器产生的纯收益和代理商的纯收益期望值分别为 由博弈论中的Nash平衡原理[12],我们知道最优策略由等式M·E[U]=E[V]确定,即 其中 下面我们分两步来求解此最优化问题.首先,在固定修理工数目N的条件下求解最优保修期.然后,根据定理3寻求最优修理工数目N∗. 定理4对固定的N,方程(3)在区间(0,L0)中恰好存在一个根的充分条件为 证明 考虑函数 易知: (i)f(0)=−∆(N); (ii)f′′(L)=P′′(L)≥ 0,即函数f(L)对于固定的N 是凸函数. 因此,根据零点定理,若f(0)f(L0)<0,即 那么方程f(L)=0在区间(0,L0)内恰好有一个根.定理得证. 将代入(2),我们得到代理商的平均收益为 其中E[W](N)是将代入E[W]后的表达式. 由于E[W](N)表达式太复杂,我们无法利用求导来得到最优修理工数目.但是,考虑到机器数目的有限性,我们可利用穷尽法来求 由此可得,最优保修期和保修价格分别为.再将N∗,L∗和P∗代入(1)和(2),我们便得到每台机器产生的最大收益以及代理商的最大收益分别为 这一节,我们利用Matlab编程提供了几个数值实例来演示模型中参数变化对最优解的影响.当然,以下数值实例中参数都是在 成立的条件下选取的.我们假设 数值仿真结果由表1和图1给出. 在表1中,我们观察到最优修理工数目N∗和代理商最大的期望收益E[V∗]随着机器数目M增加而增大.图1给出了当机器寿命L0取三个不同值时,参数R和M对最优保修期L∗的影响.从图1可看出,最优保修期L∗随着机器产生的收益R的增加而递减.而且,当机器寿命L0越大时,最优保修期L∗下降越快.然而,当机器寿命L0固定时,机器总数目M几乎不影响最优保修期L∗.此外,正如我们所预料的,最优保修期L∗是机器寿命L0的单调增函数. 表1:模型的最优解 图1:参数R,M对最优保修期的影响 本文推广了Ashgarizadeh和M urthy[3]的工作,利用多服务器排队理论和博弈理论对具有多台机器和多个修理工的机器维修服务合约进行最优设计,求得了最优保修期、保修费和修理工数目.获得了结论:最优保修期和修理工数目均与保修价格函数无关,而且,对于固定寿命的机器,机器总数几乎不影响最优保修期的设定. 参考文献: [1]Murthy D N P,Padmanabhan V.A continuous time model of warranty[D].Stanford:Graduate School of Business,Stanford University,1993 [2]Murthy D N P,Ashgarizadeh E.Optimal decision making in a maintenance service operation[J].European Journal of Operational Research,1999,116(2):259-273 [3]Ashgarizadeh E,Murthy D N P.Service contracts:a stochastic model[J].Mathematical and Computer Modelling,2000,31(10):11-20 [4]Yeh R H,Lo H.Optimal preventive-maintenance warranty policy for repairable products[J].European Journal of Operational Research,2001,134(1):59-69 [5]Pascual R,Ortega J H.Optimal replacement and overhaul decisions with imperfect maintenance and warranty contracts[J].Reliability Engineering and System Safety,2006,91(2):241-248 [6]Murthy D N P,Blischke W R.Product warranty management—III:a review of mathematical models[J].European Journal of Operational Research,1992,63(1):1-34 [7]Murthy D N P,Djamaludin I.New product warranty:a literature review[J].International Journal of Production Economics,2002,79(3):231-260 [8]Murthy D N P,Blischke W R.Warranty Management and Product Manufacture[M].Berlin:Springer Publishing,2006 [9]Huber S,Spinler S.Pricing of full-service repair contracts[J].European Journal of Operational Research,2012,222(1):113-121 [10]Xiang Y,Cassady C R,Pohl E A.Optimal maintenance policies for systems subject to a Markovian operating environment[J].Computers&Industrial Engineering,2012,62(1):190-197 [11]Gross D,Harris C M.Fundamentals of Queueing Theory[M].New York:Wiley,1985 [12]Binmore K,Rubinstein A,Wolinsky A.The Nash bargaining solution in economic modelling[J].Rand Journal of Economics,1986,17(2):176-1883 模型分析
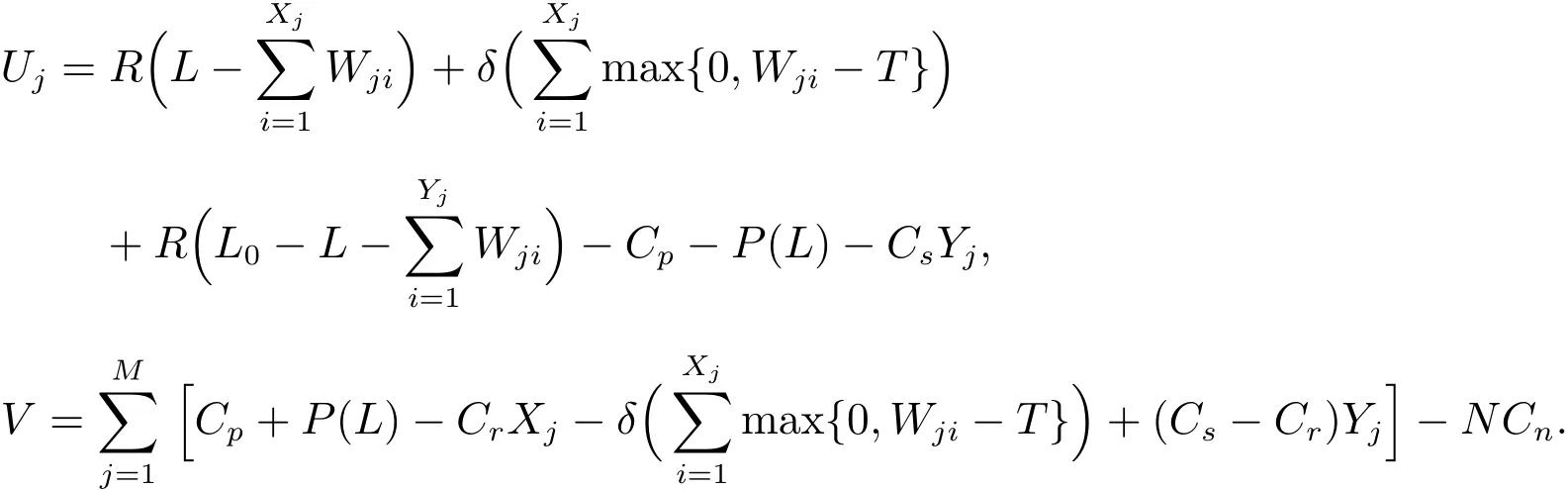
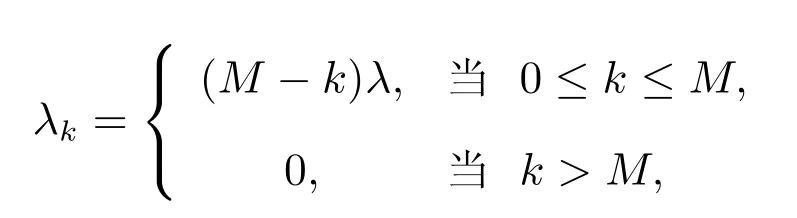
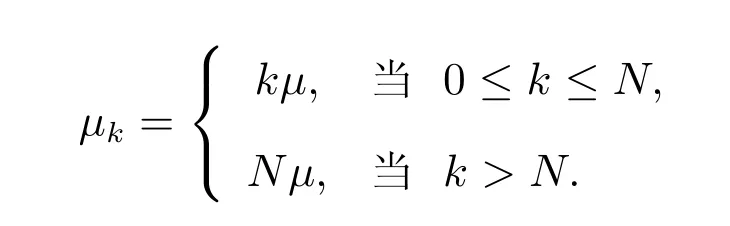
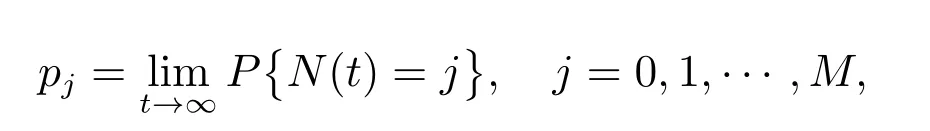
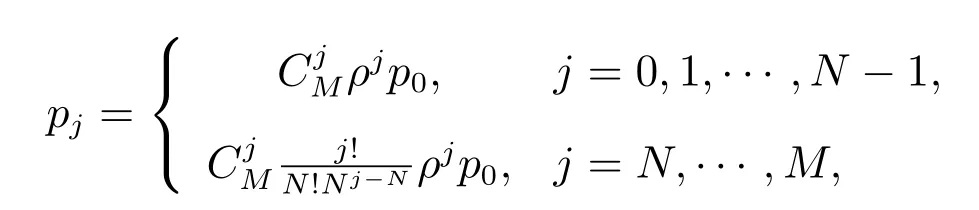
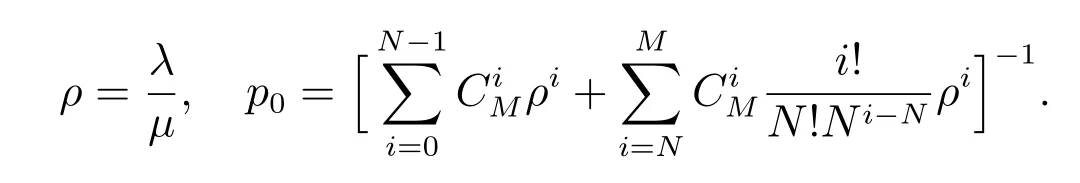
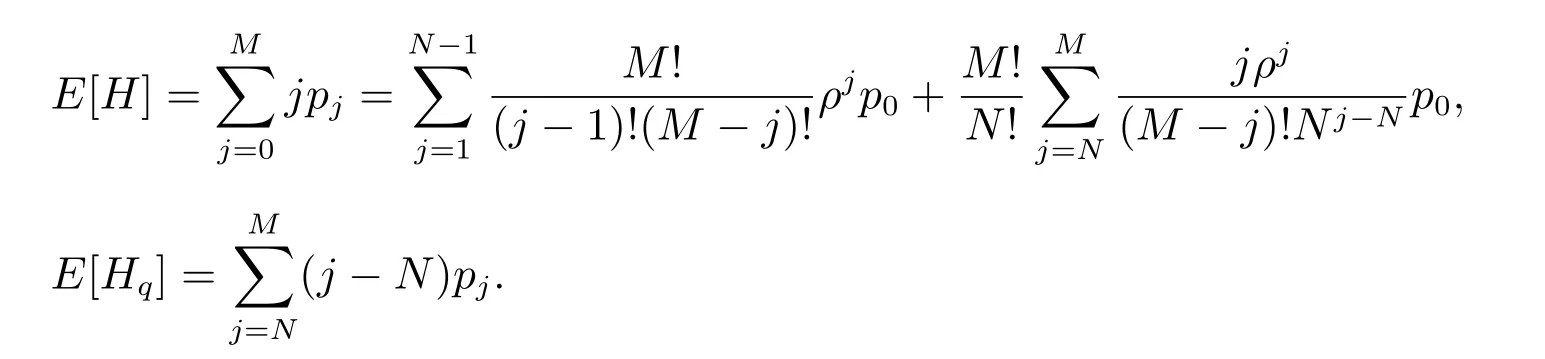

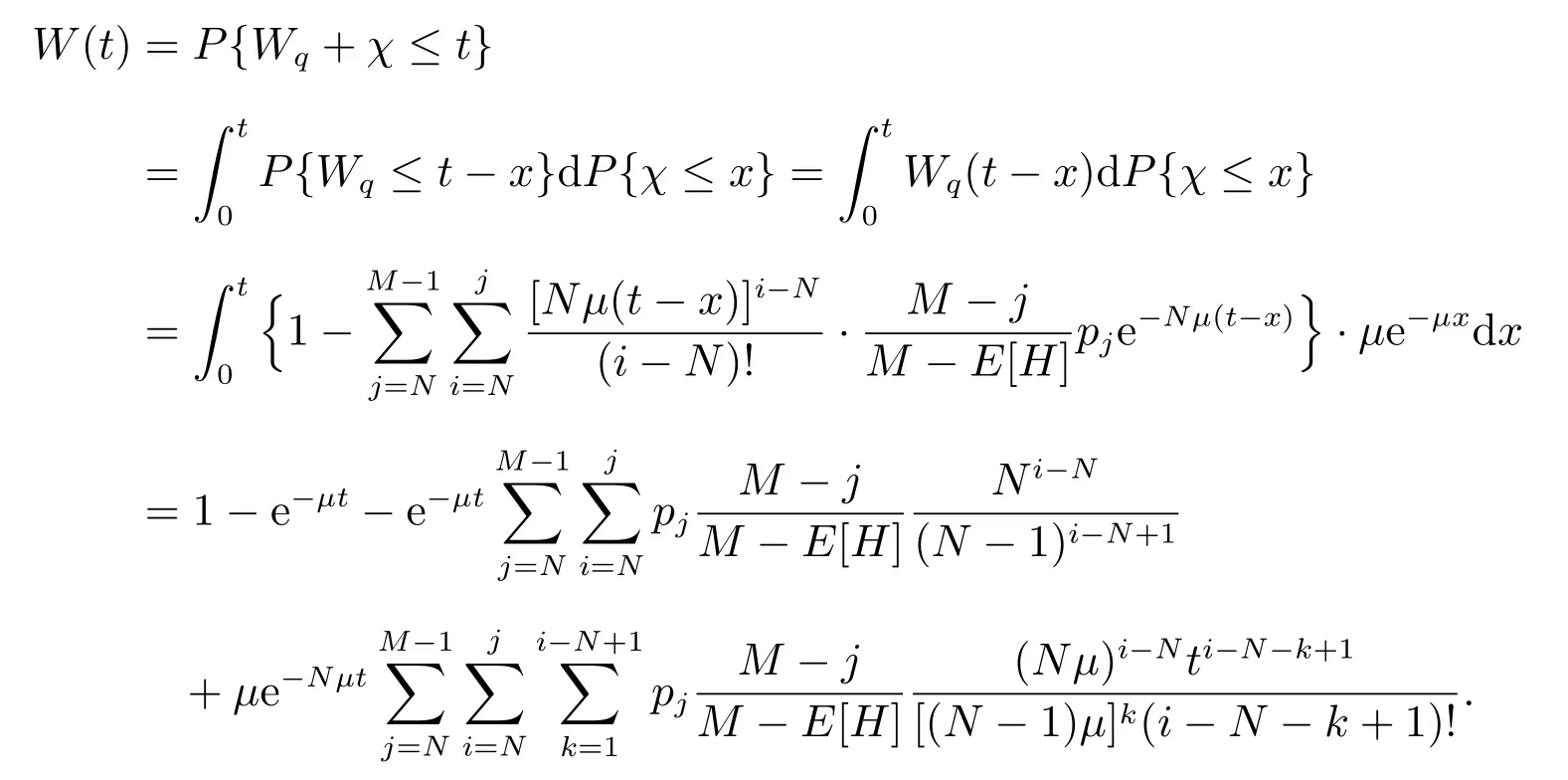


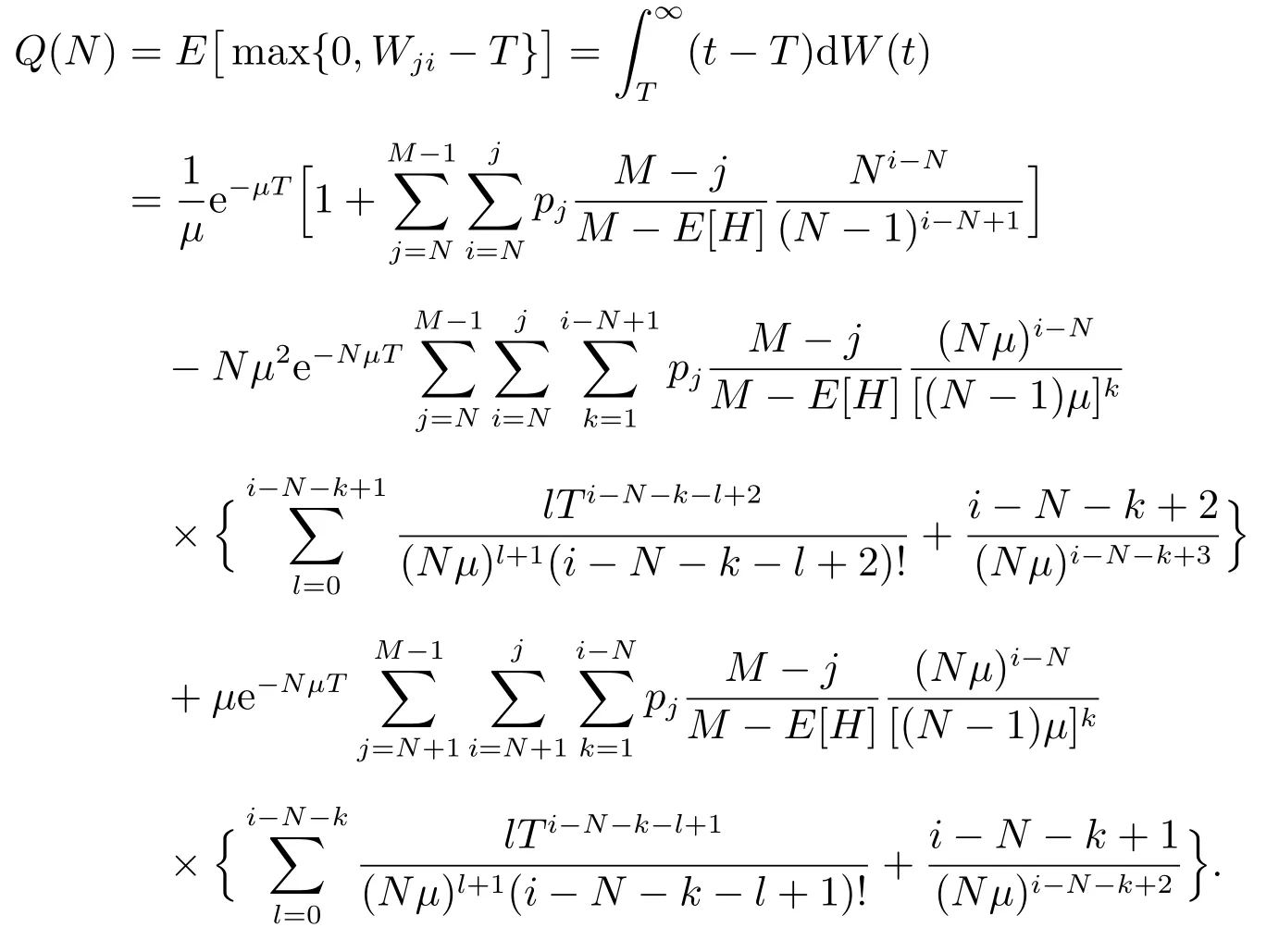
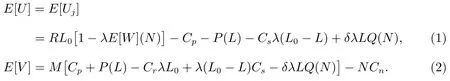
4 最优定价及设计
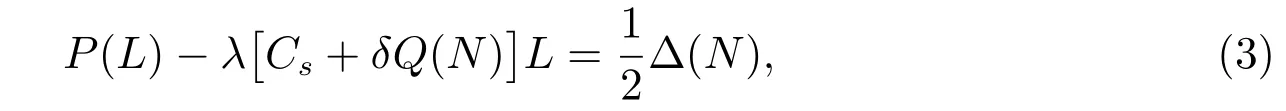



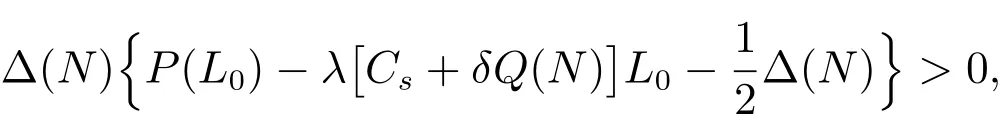

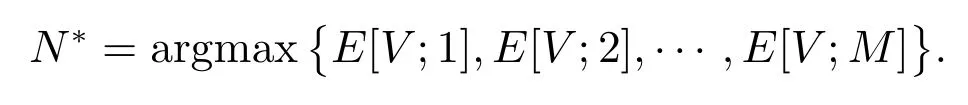

5 数值实例


6 小结

