双管Buck-Boost变换器的带输入电压前馈双闭环控制策略
颜湘武 ,王 杨 ,葛小凤 ,张 波
(1.华北电力大学 新能源电力系统国家重点实验室,河北 保定 071003;2.国网新源张家口风光储示范电站有限公司,河北 张家口 075000)
0 引言
双管Buck-Boost变换器将Buck模式和Boost模式联合使用后,具有升降压功能、功率直通通路[1]和开关管电压应力低等优点,在电池充放电及新能源发电等需要宽范围输入特性的领域得到广泛应用[2-6]。
双管Buck-Boost变换器在电感电流连续的情况下,工作在Boost模式时,控制输出电压传递函数存在右半平面零点,限制了系统带宽,降低了输入动态响应速度。文献[7]和[8]分别提出采用伪滑模控制和模型预测控制来提高控制系统的动态响应速度,但是这2种方法属于非线性控制方法,原理与设计比较复杂。由于双管Buck-Boost变换器工作在Buck和Boost模式时,其电路分别等效于传统的Buck和Boost电路,因此文献[9]提出使用传统的峰值电流控制来提高系统的动态响应速度。为了克服峰值电流法需要谐波补偿且抗干扰能力差的缺点,文献[10]提出采用平均电流控制来提高系统动态性能。但是上述2种方法不能够实现变换器在2种模式之间的自动切换,文献[11]提出双载波-单调制或者双调制-单载波的调制方法实现变换器在2种模式之间的自动近似平滑切换,但是这2种调制方式在2种模式下使用的是同一个调节器,因此Buck模式下的动态响应速度也会受到Boost右半平面零点限制的影响。文献[12]提出了带输入电压前馈的电压型控制,通过输入电压的前馈作用提高了变换器的输入动态响应速度,但是由于电压型控制未对电感或者开关管电流进行控制,需要额外的电流保护模块,同时其动态响应性能也较电流型控制差[13-14]。
为此,本文通过采用具有电压电流双闭环结构的平均电流法作为基础控制,并与双调制-单载波的调制方式相结合,在实现变换器Buck和Boost模式自动切换的同时,对电感电流进行了控制,在一定程度上提高了系统的动态响应性能。为了更好地减小Boost模式下右边平面零点对变换器整个工作范围的影响,在Buck和Boost工作模式的小信号模型基础上,推导了适用于平均电流法的输入电压前馈函数,有效地提升了变换器的输入动态响应性能,并通过仿真和实验验证了所提控制方法的有效性。
1 两模式平均电流控制原理

图1 两模式平均电流控制原理Fig.1 Principle of two-mode average current control
图1为双管Buck-Boost变换器两模式平均电流控制原理,电路拓扑中有VT1和VT22个开关管,通过控制这 2 个开关管的导通时间[15]和相位差[16]等可使变换器工作在多种工作方式下。其中比较常用的是Buck和Boost两模式工作方式。当开关管VT1高频开关、VT2常断时,为Buck模式,变换器可等效为传统的Buck变换器;当开关管VT2高频开关、VT1常通时,为Boost模式,变换器可等效为传统的Boost变换器。
在这2种模式下,变换器输入、输出电压与2个开关管占空比之间的关系都满足式(1)[1]。

其中,d1、d2分别为开关管 VT1、VT2的占空比;uo、ug分别为变换器输出与输入电压。
图1中平均电流模块由输出电压外环调节器和电感电流内环调节器共同组成电压电流双闭环结构。模式切换模块通过在平均电流模块输出的调制信号uc上叠加一个偏移量ubias实现2种模式的自动切换,其原理如图2所示。

图2 两模式切换控制方法波形图Fig.2 Waveforms of mode switching control
图2所示为双调制-单载波模式自动切换方法,通过在调制信号uc上叠加ubias得到调制信号uBuck和uBoost,并分别与同一个载波信号作比较来得到开关管VT1和VT2所需的占空比。从图2中可看出,当2个调制信号之间的差值ubias小于锯齿波的峰峰值u2-u1时,调制信号uBuck和uBoost在模式切换点处就会同时与载波相交,从而进入Buck-Boost工作模式[2]。为了降低开关损耗,防止变换器在模式切换过程中进入Buck-Boost工作模式,调制信号需要满足式(2)。

为了使变换器不脱离开关管的调节作用,一般要求在任何时刻,至少有1个开关管处于高频开关的状态,因此通常要求ubias=u2-u1。这同时也是实现Buck和Boost 2种模式自动平滑切换的条件[12]。
2 输入电压前馈的引入
2.1 输入电压前馈函数的推导
前馈控制能够很好地抑制甚至消除扰动信号对控制量的影响,图3为输入电压前馈控制框图。
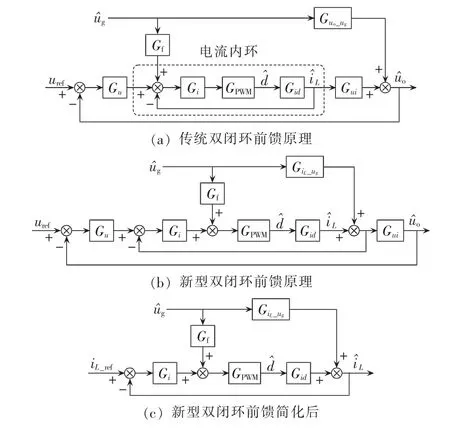
图3 输入电压前馈控制框图Fig.3 Block diagram of input voltage feedforward control
前馈控制由于较易受系统模型准确性的影响,常常与反馈控制联合使用,图3(a)所示为传统的双闭环扰动前馈原理。图3中,Gi和Gu分别为电流调节器和电压调节器的传递函数,Gid和Gui分别为控制到电感电流和电感电流到输出电压的传递函数,为输入电压扰动到输出电压的传递函数,Gf为输入电压前馈函数,GPWM为调制器的传递函数,它们在Buck和Boost模式下的表达式可参考文献[12];分别为变换器输出电压、输入电压、电感电流、开关管占空比的扰动量。
从图3(a)中可以看出,传统的双闭环输入电压前馈方法[17]是将经过前馈函数处理过的输入电压扰动信号前馈至外环电压调节器的输出侧。前馈函数的结果如式(3)所示。

Gf在Buck和Boost 2种工作模式下的具体表达式分别如式(4)和(5)所示。
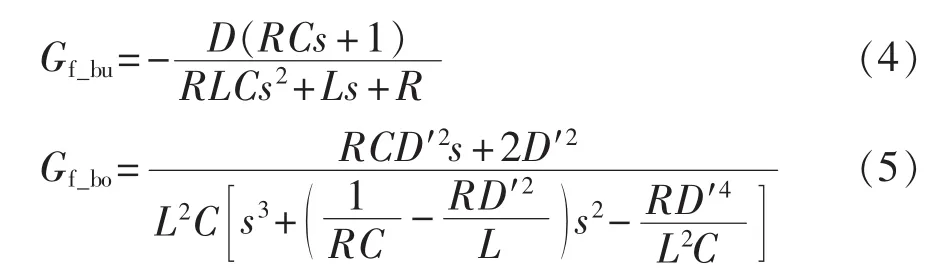
式(4)和式(5)中,D 为对应开关管的占空比且D′=1-D;R、L和C分别为变换器负载电阻、电感和电容。从上述两式可以看出,2种模式下的输入电压前馈函数形式复杂,在物理上很难实现,会大幅增加控制系统的设计难度。从图1双管Buck-Boost变换器的拓扑结构可以看出,输入电压的扰动会首先传递到电感电流,然后再传递至输出侧电容,最终导致输出电压的波动,若是能够通过输入电压前馈提前将电感电流上的波动进行抑制,不仅可以很好地限制电感电流的幅值,而且可以更加快速地抑制输出电压的波动,保持稳定的输出。
图3(b)所示为新型双闭环前馈的原理图。图中iL_ref为电压外环输出的电感电流给定值,GiL_ug为输入电压扰动到电感电流的传递函数。从图3(b)中可以看出,新型的前馈控制方法通过将输入电压直接前馈至电流内环的电流调节器的输出侧,将输入电压的波动直接在电流内环进行抑制,保持电感电流的稳定,减小输入电压扰动对输出电压的影响。由于将前馈作用移至了内环,所以可将外环略去,化简后见图3(c),新型的输入电压前馈函数如式(6)所示。

其中,GPWM一般等效为一个比例环节[12],如式(7)所示。
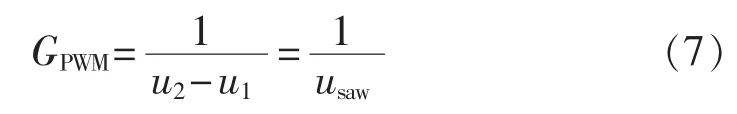
其中,u1、u2分别为图2中高频载波的谷值和峰值,并将峰值与谷值之差定义为载波峰峰值,用usaw表示。
Gf在Buck和Boost 2种模式下的具体表达式分别如式(8)和(9)所示。

从式(8)和式(9)可以看出,其形式较传统的双闭环前馈较易化简。Buck模式下的输入电压前馈函数只与输入、输出电压的静态工作点和载波幅值有关。Boost模式下,还与频率有关系,但是由于传统的新能源发电和充电设备的输出电压的波动频率往往很低可以近似等效为 1[12],因此输入电压前馈函数的值将主要受所选静态工作点的影响。随着静态工作点的变化,前馈函数的表达式不发生变化,只是其值会改变,并在所选静态工作点处具有最好的前馈效果,其余范围前馈作用将稍微弱化。本文由于采用电压电流双闭环结构的平均电流法,其本身就具有较快的输入动态响应速度[14],可以在前馈作用较弱处起到补偿效果,因此本文将静态工作点选在模式切换处,在加强变换器模式切换处的输入动态响应性能的同时,实现前馈函数的统一。因此,2种工作模式下的输入电压前馈函数可以最终化简为式(10)。
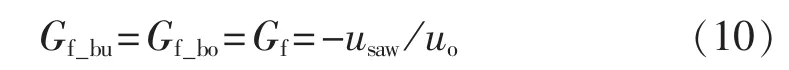
2.2 带输入电压前馈的两模式平均电流控制策略
图4所示为带输入电压前馈的两模式平均电流控制策略图,图中Gf为新型输入电压前馈函数。从图中可以看出,输入电压信号经过前馈函数的处理后,分别与调制信号uBuck和uBoost叠加再经过比较器的调制后就可以得到所需的PWM波。并且,从式(10)可以看出,由于2种模式下的输入电压前馈函数相同,不再需要对ubias进行调整,直接令其与高频载波相等即可实现变换器2种模式的自动平滑切换。

图4 带输入电压前馈的两模式平均电流控制策略Fig.4 Two-mode average current control combined with input voltage feedforward
2.3 仿真比较
本文利用MATLAB/Simulink软件搭建了仿真模型,对所提控制方法进行了仿真分析,并与单环的电压型控制进行比较。仿真参数如下:输入电压为100~400 V,输出电压为200 V,输出功率为 800 W,负载电阻为50 Ω,电感为4 mH,开关频率为30 kHz,输出侧电容为 490 μF,输入侧电容为 220 μF,开关管型号为IKW40N120H3,二极管型号为IDW20G1-20C5。图5为变换器输入电压到输出电压的波特图。

图5 输入电压到输出电压的波特图Fig.5 Bode diagrams of input voltage and output voltage
图5中单环指的是只有电压环的电压型控制,单环前馈指的是带输入电压前馈的电压型控制,双环指的是本文中提到的具有电压电流双闭环结构的平均电流控制,双环前馈指的是带输入电压前馈的平均电流控制。图5(a)和(b)所示分别为变换器在输入电压为100 V和400 V时,各种控制方法的幅频和相频响应特性。从图5中可以看出,在2种工作模式下,在低频范围内,双环控制的输入动态响应比单环好,且加入输入电压前馈后,都能够有效增强其输入动态响应性能,其中带输入电压前馈的双闭环控制具有最好的动态响应性能。
图6所示为变换器在Boost模式下,输入电压从120 V变为170 V时,电感电流iL和输出电压uo在4种控制方法下的仿真波形图。图7所示为变换器在Buck模式下,输入电压从220 V变为270 V时,各个状态量的仿真波形图。
从图6和图7中可以看出,当输入电压ug发生变化时,会在电感电流和输出电压上造成一个很大的冲击。当不加输入电压前馈时,单环控制下,电感电流和输出电压的冲击会远远超出允许的范围;双环控制下,冲击虽然会有所减小,但还是不能够满足部分场合的要求。当加入输入电压前馈后,单环和双环控制下的输出电压和电感电流的冲击得到了很好的抑制,但是由于单环电压型控制动态响应速度慢,电路要经过一定的振荡后才能够达到稳定状态,这不仅会给下级设备带来不稳定因素,也会加大变换器的功率损耗和电磁干扰,而双环控制则由于具有很快的动态响应速度,能够很快地在前馈控制粗调的基础上进行微调,使电路实现稳定的输出,同时还对电感电流进行了控制,保证了设备的安全稳定运行。图8所示为变换器在Buck和Boost 2种模式之间互相切换时的仿真波形图。从图8中可以看出,当变换器的输入电压在150~250 V之间变化时,在没有加入输入电压前馈时,电感电流和输出电压上都会产生一个冲击,单环电压型控制由于动态性能较差,且没有对电感电流进行控制,导致电感电流上的冲击往往会超出允许值。在加入输入电压前馈后,变换器抑制输入电压波动的能力大幅增强,能够很快地根据输入电压的变化完成模式的切换。但是,单环电压型控制在模式切换完成后,还需要一定时间的振荡过程才能实现稳定的输出,动态响应较慢。带输入电压前馈的双闭环控制能够在前馈的作用上很快地实现稳定输出,使变换器能够根据输入电压的变换自动完成两模式的平滑切换。

图6 Boost模式下输入电压跃变仿真波形Fig.6 Simulative waveforms of input voltage step-change in Boost mode

图7 Buck模式下输入电压跃变仿真波形Fig.7 Simulative waveforms of input voltage step-change in Buck mode

图8 两模式切换的仿真波形图Fig.8 Simulative waveforms of mode switching
3 实验验证
为了验证所提带输入电压前馈的电压电流双闭环控制方法的有效性,在实验室搭建了一台800 W的试验样机,其参数与仿真参数一致。
由于变换器工作在两模式下时可以分别等效为传统的Buck和Boost电路,已有大量文献对其参数的设计进行了讨论,具体的设计步骤和方法可以参考文献[18]。同时为了方便开关管的选取和变换器容量的提升,本文中所选取开关管的开关频率为30 kHz,电压和电流调节器使用传统的PI调节器。
图9和图10分别为输入电压在120~170 V和220~270 V之间变化时,电感电流和输出电压的实验波形图。从图9和图10中可以看出,在不加入输入电压前馈时,输入电压发生变化时,会在电感电流和输出电压上产生冲击,严重时甚至会烧毁开关管,危及设备工作安全。从图9(b)和10(b)中可以看出,加入输入电压前馈后,能够大幅提高变换器的输入动态响应性能,很好地抑制输入电压波动对变换器的影响,保证稳定的输出,同时还可以有效控制电感电流的大小,防止电流过大烧毁设备。

图9 Boost模式下输入电压跃变实验波形Fig.9 Experimental waveforms of input voltage step-change in Boost mode
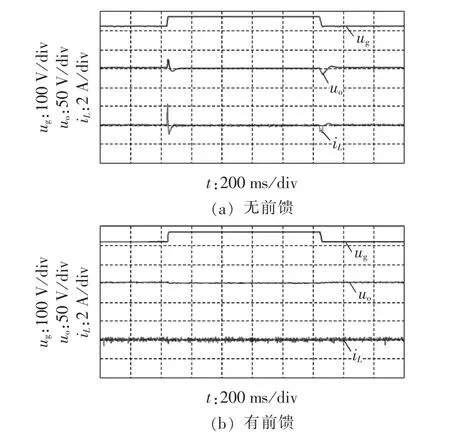
图10 Buck模式下输入电压跃变实验波形Fig.10 Experimental waveforms of input voltage step-change in Buck mode
图11所示为输入电压在150~250 V之间变化时的实验波形图。从图11(a)中可以看出,变换器在Buck和Boost模式切换时,电感电流存在较大的冲击,这不仅会导致输出电压产生波动,严重时可能还会烧毁电感和开关管,因此十分有必要对电感电流进行适当的控制。从图11(b)可以看出,输入电压前馈的引入,可以很好地抑制电感电流和输出电压的波动,实现变换器2种模式的自动平滑切换,与理论和仿真结果相符。
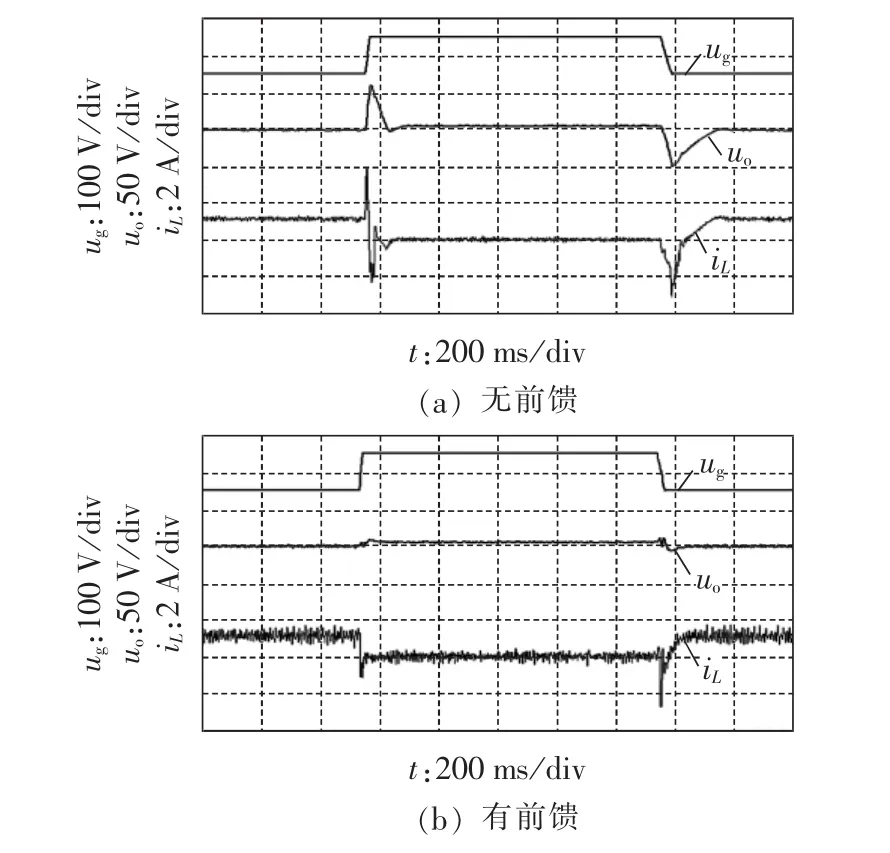
图11 两模式切换的实验波形Fig.11 Experimental waveforms of mode switching
4 结论
本文针对双管Buck-Boost变换器的两模式控制策略进行了研究,提出了带输入电压前馈的两模式电压电流双闭环控制策略。该控制策略加入了电流内环,不仅对电感和开关管的电流进行了控制,有效地保护了设备的安全,而且能够提高变换器的动态响应性能。同时,将输入电压前馈引入了电流内环,克服了传统双闭环前馈函数难以实现和化简的缺点,并利用了内环的快速调节特性,很好地抑制了输入电压波动对电感电流和输出电压的影响。最后实验室通过搭建仿真模型和800 W的试验样机,验证了所提控制策略的有效性。
参考文献:
[1]CHEN J,MA KSIMOVICD,ERICKSON R.Buck-BoostPWM converters having two independently controlled switches[C]∥2001 IEEE 32nd Annual Power Electronics Specialists Conference,2001. [S.l.]:IEEE,2001:736-741.
[2]MA Y,WANG H,CHEN G,et al.A novel method for smooth transition in step-up /step-down DC-DC converter[C]∥IEEE InternationalConference ofElectron Devicesand Solid-State Circuits,2009.Hong Kong,China:IEEE,2009:95-98.
[3]QIAO H,ZHANG Y,YAO Y,etal.AnalysisofBuck-Boost converters for fuel cell electric vehicles[C]∥IEEE International Conference on Vehicular Electronics and Safety,2006.Shanghai,China:IEEE,2006:109-113.
[4]晏坤,王辉,漆文龙,等.微电网储能系统中基于PWM加双重移相控制的双向DC/DC变换器研究[J].电力自动化设备,2015,35(4):44-52.YAN Kun,WANG Hui,QI Wenlong,et al.Bidirectional DC /DC converterbased on PWM plus dualphase-shiftcontrolfor microgrid storage system[J].Electric Power Automation Equipment,2015,35(4):44-52.
[5]邾玢鑫,程杉,谭超.ZVS隔离型高增益DC/DC变换器[J].电力自动化设备,2015,35(5):70-76.ZHU Fenxin,CHENG Shan,TAN Chao.ZVS isolated high stepup DC /DC converter[J].Electric Power Automation Equipment,2015,35(5):70-76.
[6]杨亮,苏剑,刘海涛,等.单相并网逆变器的直流分量抑制策略[J]. 电力自动化设备,2015,35(4):145-150.YANG Liang,SU Jian,LIU Haitao,et al.DC component suppression strategy for single-phase grid-connected inverter[J].Electric Power Automation Equipment,2015,35(4):145-150.
[7]AGOSTINELLI M,PRIEWASSER R,MARSILI S,et al.Fixedfrequency pseudo sliding mode control for a Buck-Boost DC-DC converter in mobile applications:a comparison with a linear PID controller[C]∥2011 IEEE International Symposium on Circuits and Systems(ISCAS).Rio de Janeiro,Brazil:IEEE,2011:1604-1607.
[8]MARIETHOZ S,ALMER S,MORARI M.Optimal control of a two control input Buck-Boost converter[C]∥48th IEEE Conference on Decision and Control,2009 Held Jointly with the 2009 28th Chinese Control Conference.CDC /CCC 2009.Shanghai,China:IEEE,2009:6575-6581.
[9]LEE Y H,HUANG SC,WANG SW,etal.Power-tracking embedded Buck-Boost converter with fast dynamic voltage scaling for the SoC system[J].IEEE Transactions on Power Electronics,2012,27(3):1271-1282.
[10]HWANG B H,SHEEN B N,CHEN J J,et al.A low-voltage positive Buck-Boost converterusingaverage-current-controlled techniques[C]∥2012 IEEE International Symposium on Circuits and Systems(ISCAS).Seoul,Korea:IEEE,2012:2255-2258.
[11]LEE Y J,KHALIGH A,EMADI A.A compensation technique for smooth transitions in a non-inverting Buck-Boost converter[J].IEEE Transactions on Power Electronics,2009,24(4):1002-1015.
[12]姚川,阮新波,曹伟杰,等.双管Buck-Boost变换器的输入电压前馈控制策略[J]. 中国电机工程学报,2013,33(21):36-44.YAO Chuan,RUAN Xinbo,CAO Weijie,et al.An input voltage feedforward control strategy for two-switching Buck-Boost DC-DC converters[J].Proceedings of the CSEE,2013,33(21):36-44.
[13]周国华,许建平.开关变换器调制与控制技术综述[J].中国电机工程学报,2014,34(6):815-831.ZHOU Guohua,XU Jianping.A review ofmodulation and control techniques for switching converters[J].Proceedings of the CSEE,2014,34(6):815-831.
[14]DIXON L H.Average current mode control of switching power supplies[J].Unitrode Product&Applications Handbook,1990,1:356-369.
[15]任小永,阮新波,李明秋,等.双沿调制的四开关Buck-Boost变换器[J]. 中国电机工程学报,2009,29(12):16-23.REN Xiaoyong,RUAN Xinbo,LIMingqiu,etal.Dualedge modulated four-switch Buck-Boost converter[J].Proceedings of the CSEE,2009,29(12):16-23.
[16]肖华锋,谢少军.用于光伏并网的交错型双管Buck-Boost变换器[J]. 中国电机工程学报,2010,30(21):7-12.XIAO Huafeng,XIE Shaojun.An interleavingdoubleswitch Buck-Boost converter for PV grid connected inverter[J].Proceedings of the CSEE,2010,30(21):7-12.
[17]金以慧.过程控制[M].北京:清华大学出版社,1993:125-134.
[18]曹伟杰.双管Buck-Boost变换器的输入电压前馈控制方法[D].南京:南京航空航天大学,2011.CAO Weijie.Input voltage feed-forward control method of twoswitch Buck-Boost converter[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2011.

