电动汽车换电站调度优化问题下的约束罚函数

张 颖，容展鹏，张宇雄，扈海泽，赵 军，韦 梦，方梦鸽

（长沙理工大学 电气与信息工程学院，湖南 长沙 410004）

0 引言

全球能源和环境问题日益严峻，具有可再生性的风、光等分布式电源和电动汽车越来越受到人们的重视，被视为未来能源和交通工具的发展趋势。风、光等分布式电源具有间歇性、随机性的特点，其大规模接入微电网将给电网带来较大的冲击，而有序控制的电动汽车充电计划能降低总充电成本与系统网损、削峰填谷、平抑可再生能源的间歇性［1］。间歇性分布式电源的输出功率具有较大的波动性，电动汽车换电站应设置较小的调度时间间隔以应对分布式电源的波动性，通常以1 d为一个调度周期，减小调度间隔将成倍增加调度优化的求解维数；同时由于电动汽车较高的电池造价，过大的运营库存备用和充电设备容量无疑会带来过大的基础设备投资，不利于电动汽车换电站的快速推广，采用更为苛刻的约束空间更符合工程实际，从而将给优化带来高维、高约束的问题。

在电动汽车优化调度研究方面，目前主要包括：对电动汽车模型的完善，如电池的充电损耗、电池的充放电效率、换电站的运营特性等；对各类充放电环境的综合考虑，如可再生分布式电源、需求侧管理模式等；对不同目标函数的研究。具体的例子有：文献［2］分析了电网调峰对风电消纳的影响，风电-电动汽车协同利用能提高风电消纳水平并实现节能减排；文献［3］以电网负荷波动和用户成本最小为目标函数，对比分析了不同分时电价模式对调度策略的影响；文献［4］将电动汽车互动意愿加入电网电价制定模型，通过基于价格的需求响应引导电动汽车实现电网调峰；文献［5］建立了用户侧、电网侧两端优化模型，用户侧考虑电动汽车用户的个性化需求，电网侧采用包含经济、环境污染、风电弃用的多目标优化模型；文献［6］为电动汽车调度优化算法的研究设计了一种改进的思维进化算法。

罚函数法是求解约束优化问题的常用方法之一，其基本思想是借助罚函数将约束问题转化为无约束问题，从而用无约束问题的方法进行求解［7］。这一思想提出至今，国内外已有众多学者对这一问题进行了广泛的研究，文献［8］提出了非固定多段映射的处理方法；文献［9］则针对遗传算法的特性，提出了一种综合罚函数；文献［10］以粒子群优化算法为基础，设计了离散化的罚函数；文献［11］在文献［10］的基础上，针对罚函数约束处理中难以设置通用惩罚因子的缺陷，提出了免参数设置的自适应罚函数法；文献［12］提出了基于自学习迁移粒子群优化算法及高斯罚函数的无功优化方法。

罚函数的设置对粒子群优化算法的性能有着极其重要的影响，罚函数设置过大，将会迅速降低粒子群体的多样性，并出现过约束的问题，易陷入局部最优解；如果设置过小，则不能达到理想的约束效果。传统的处理方式是，对罚因子取一个严格递增的正数列，以同时兼顾前期的多样性保持和后期的约束收敛。同时，约束问题的最优解往往位于可行域的边界上［11］，而且对高维、高约束问题因约束问题错综复杂，存在可行域分散、连续性差的特点，研究一种边界寻优能力强、对边界具有一定穿透力的罚函数处理方法将对电动汽车换电站调度优化具有重要意义。

对此，提出了基于正弦函数周期性变化构建的穿透罚函数，每一个正弦周期即一个穿透周期，在周期低谷区域产生逃逸粒子对边界区域进行穿透寻优，在周期高峰区域对逃逸粒子产生约束引力拉回可行域。粒子在对边界区域的往复穿透过程中更易在边界区域找到最优解，同时相对于传统罚函数更易突破罚函数产生的边界壁垒在附近其他可行域发现更优解。罚函数在整个增广目标函数中占的比重也在发生周期性的变化，因此全局最优解亦随之发生周期性变化，将有利于跳出局部最优解，提高算法的全局搜寻能力，起到等效的变异效果。考虑粒子的多样性保持和优化的约束收敛，对罚函数进行了分段处理，第一段为多样性保持段，第二段为穿透寻优段，第三段为约束收敛段。

1 换电站调度策略模型

电动汽车换电站的调度优化模型众多。本文以负荷波动方差、充电经济性、可再生能源消耗构成多目标优化模型。以1 d作为一个调度周期，全天分为若干个调度间隔时段。其优化目标具体如下。

1.1 负荷波动方差目标函数

负荷波动方差可表示为：

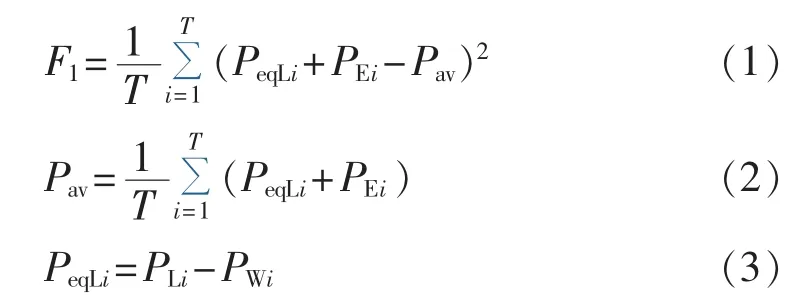
其中，F1为负荷波动方差函数；T为1 d中的调度间隔时段数；PeqLi为i时段除换电站负荷外的其他负荷减去风电机组出力后的等效负荷；PLi为除换电站负荷外的其他负荷在i时段的预测量；PWi为i时段风电机组的预测出力；PEi为换电站在i时段的充电功率；Pav为考虑换电站优化后的日平均负荷。

1.2 充放电经济性目标函数

以供电企业提供的分时电价为基础，通过合理规划充放电使电动汽车换电站充电费用最小。电动汽车换电站由电网公司负责运营，以文献［13］中提出的控制方式进行充电。当充电功率不大时，以控制充电电池规模代替控制充电电池电流进行充电功率调节，电池均处于最优充电电流下工作，电池的充电效率最优，对电池寿命损耗最小，该状态下电池的损耗费用由其对应的商业需求为其买单，这里不予计算。当充电功率较大时，所有充电电池均以大于最佳充电电流的电流充电，则会产生因充电电流过大带来的电池附加损耗。当电池处于放电状态，则其对应的商业需求服务对象为电网公司，电网公司需为此过程的电池损耗买单。

其中，F2为充放电费用函数；ji为i时段的分时电价；Pbest为单台电池最佳充电电流下的功率，此模型采用简化处理，以常数Pbest代替最佳充电功率曲线；N为全部电池数量；a1、a2为附加电池损耗费用系数；b1为放电电池损耗费用；b2为电池基本损耗费用。

1.3 充电消耗风电资源占比目标函数

充电消耗风电资源占比的表达式为：

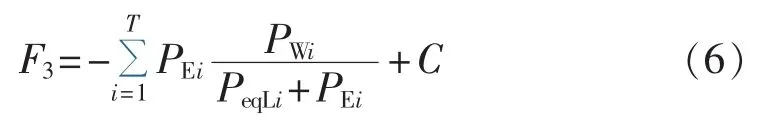
其中，F3为充电消耗风电资源占比函数，其目的是提高充电消耗能源的清洁能源占比，为与前面2个最小化函数一致进行了相反数处理；C为一适当大的正常数，其目的是对目标函数进行非负处理，以方便后面权重的确定。

1.4 多目标函数的处理

由文献［14］所述方法，可采用线性加权求和法将多目标函数转化为单目标函数进行求解。α定权法可用于权重系数的求解［14-15］。转化后的目标函数为:

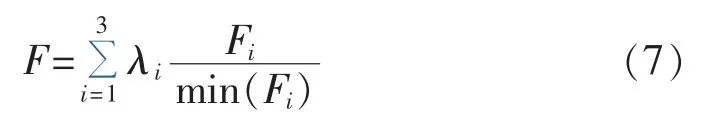
其中，min（Fi）（i=1，2，3）为单目标函数的最小值，其目的是为了统一多目标函数量纲；λi为单目标函数的权重系数。

α定权法的定义如下。

设 fi=Fi／min（Fi），xj（j=1，2，3）为 fi对应的最小值点，同时矩阵A的元素aij有：

α定权法的系数求解方程为：

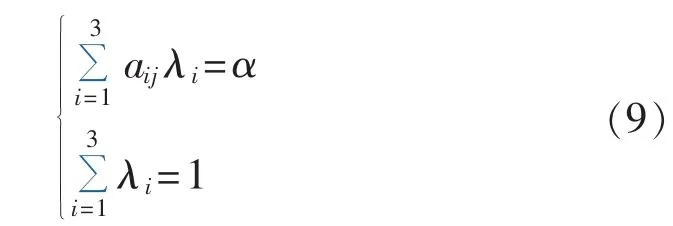
可求解得：

其中，e=［1，1，1］T。

1.5 约束条件

（1）等式约束。

其中，Ppre.all.d为优化区域内全部换电站在一个调度周期运营预测容量换算的充电负荷；Pyestd.rev为换电站修正功率，是前日的运营预测和实际运营之间的负荷差值。

（2）充电功率约束。

其中，PEi.max为换电站在i时段的最大充电功率，由充电设备和可充电电池、输电线路的情况共同决定，取三者的最小值。

（3）风电出力约束。

其中，PWi.max为风电机组在i时段的最大出力，由风电机组容量和输电线路的情况共同决定，取二者的最小值。因本文研究侧重于电动汽车及罚函数算法，采用简单模型，忽略风电机组有功出力与可吸收无功之间的约束。

（4）电池储备电量约束。

充电状态下有：

放电状态下有：

其中，Qi为换电站在i时段的电池储备容量；Qimin为i时段换电站整体最小警戒电量；Qmax为换电站所能提供的最大容量空间；Qprei为i时段换电站电池销售电量的预测值；Δt为一个调度时间间隔时长；β1为电池充电效率；β2为电池放电效率。

这一约束问题是电动汽车调度优化相对于电力系统其他调度优化的特殊问题。前一维变量的求解取值将直接影响后面变量的约束空间。因此，该问题是一个高维数约束空间随低维数变量取值动态变化的约束问题，使可行域变得错综复杂。

图1所示曲线为下文算例优化得到的换电站电池储备容量曲线。相关详细内容见本文第4节算例分析与验证，此处仅对约束特性进行简单说明。由图1可知，为充分利用电动汽车的削峰填谷作用，电池储备容量将在系统负荷低谷区后达到容量上限，并尽可能地更长时间维持容量上限，以在负荷尖峰时减少充电出力；在换电站销售高峰后、负荷低谷优惠电价到来前则处于容量下限。由此可见，将有大量变量的取值位于约束边界上。

图1 电池储备容量曲线Fig.1 Reserve capacity curve of battery

2 粒子群优化算法分段穿透罚函数

2.1 粒子群优化算法和罚函数简介

对罚函数的详细介绍可见文献［7］，其带罚函数的增广目标函数为［7］：

其中，δ为罚因子；Bi（x）为惩罚项；f（x）为原目标函数；hi（x）为等式约束项；gi（x）为不等式约束项；l为等式约束数量；m为等式约束和不等式约束数量之和。

粒子群优化算法的核心内容——位置迁移的表达式为［16-17］：

其中，vi.n（k）为第i个粒子的第n维在第k次迭代时的速度；xi.n（k）为第i个粒子的第n维在第k次迭代时的位置；pbest为个体最优位置；gbest为全局最优位置。

因粒子群优化算法的应用已比较普遍，其他参数及算法的详细情况见文献［16-17］。

当δ设置过大时，可行域外的粒子的增广目标函数值F′将远远大于可行域内粒子的F′值，则可行域外的粒子将在式（19）gbesti.n-xi.n（k）项的不断作用下迅速向可行域内迁移，使得粒子的多样性变差，同时亦会造成过约束。当δ设置过小时，将不能达到理想的约束效果。实际计算中，罚因子的设置十分重要［2］。文献［2］给出一种传统的处理方法，即将δ设置为一个趋向足够大的严格递增正数列。本文提出的分段穿透罚函数，其主要对罚因子δ随迭代次数（epochs）的动态变化进行研究。

2.2 分段穿透罚函数

（1）多样性保持段罚函数。

罚函数在多样性保持阶段，采用了从原点出发逐步振荡发散的罚因子设计。从原点出发逐步振荡增大，有利于在寻优初期维持可行域外的粒子的增广目标函数值F′与可行域内粒子的F′值相差不大，有利于多样性的维持。多样性保持阶段的罚函数为：

其中，k1为穿透周期高峰区间约束引力递增系数；ep为迭代次数，ep∈（0，ep1］，（0，ep1］为多样性保持段所在区间，ep1应为周期T′的整数倍；T′为穿透周期长度；k2为穿透力度递减系数，k2ep的乘积越大粒子的穿透力度越小，逐步递减的设计有利于保障收敛。其函数图像如图2所示。

图2 多样性保持段罚函数曲线Fig.2 Penalty function curve in diversity-maintaining period

（2）穿透寻优段罚函数。其中，穿透寻优段罚函数采用了固定的穿透力度值k3；ep∈（ep1，ep2］，（ep1，ep2］为穿透寻优段罚函数所处区间，同样ep2也应为周期T′的倍数；k′1的含义与式（20）中k1相同，并取k′1＞k1。

为保证罚函数的连续性，应有：

穿透寻优段罚函数的函数图像如图3所示。

图3 穿透寻优段罚函数曲线Fig.3 Penalty function curve in penetration-optimizing period

（3）约束收敛段罚函数。

约束收敛段罚函数采用了文献［6］提出的自适应罚函数处理方法。其数学表达式为：

其中，z为约束适应度函数；k为罚因子递增系数；k′3是为了保障函数的连续性；ep≥ep2。

对违反约束的粒子，其惩罚力度与离边界的距离成正比。因此，粒子在边界附近仍具有较大的穿透力度，有利于保持算法在约束收敛过程中的边界寻优能力。为使函数具有更好的连续性和通用性，采用曲线拟合的方法进行优化。

2.3 穿透罚函数的先进性分析

2.3.1 双向边界寻优特性

双向边界寻优特性分析图见图4。在穿透周期低谷区域（xT′-t，xT′+t）将产生逃逸粒子进入非可行区域（t为小于T′／4的某一正数，x为任意自然数），逃逸粒子在穿透周期高峰区域（t／2+xT′-t，t／2+xT′+t）将在约束引力的作用下逐步往边界区域寻优。而传统的罚函数处理方法，因粒子难以有效突破罚函数产生的边界壁垒，只具有单向寻优的能力。双向边界寻优能力将使粒子在对边界区域的往复穿透过程中更易在边界区域找到最优解。

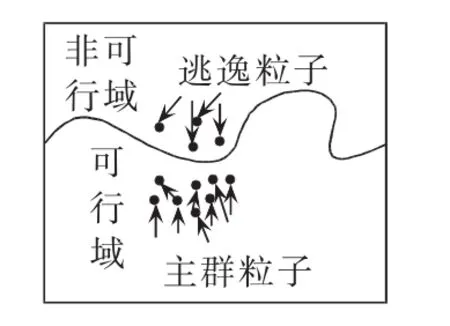
图4 双向边界寻优特性示意图Fig.4 Schematic diagram of bidirectional boundary optimization

2.3.2 捷径寻优特性

捷径寻优特性分析图如图5所示。设图中B点为全局最优位置，A点为局部最优位置。传统的罚函数最佳寻优路径为沿边界曲线ACB进行寻优，而穿透罚函数可以在穿透周期低谷区间（xT′-t，xT′+t）突破边界沿捷径AB进行寻优。因此，相对于传统罚函数其更易突破罚函数产生的边界壁垒在附近其他可行域发现更优解，有利于增强粒子在错综复杂可行域环境下的寻优能力。

图5 捷径寻优特性示意图Fig.5 Schematic diagram of shortcut optimization

2.3.3 等效变异特性

等效变异特性分析图如图6所示。随着穿透罚函数的周期性变化，整个罚函数在增广目标函数F′中所占比例也相应发生周期性的变化。当位于穿透低谷区域（xT′-t，xT′+t）时，边界约束力减弱，原位于可行域内的全局最优位置gbest-A将极可能被逃逸粒子取代，即在非可行域内被gbest-B取代。由式（19）可知粒子的迁徙方向也将发生变换，改变粒子的搜寻区域，将有助于粒子跳出局部最优解，增强全局搜寻能力，起到等效变异的效果。文献［18］提出的改进粒子群优化算法的变异表达式为：

图6 等效变异寻优特性示意图Fig.6 Schematic diagram of equivalent mutation optimization

其中，gbest.i为 gbest（全局极值）的第 i个变量；γ 为随机变异变量，服从 Gauss（0，1）分布。

穿透罚函数亦能起到类似的改变全局最优位置的变异效果。同时，gbest-B理论上位于边界区域附近，其变异具有选择导向性，有利于粒子边界寻优能力的增强。

3 算法参数设置与求解流程

本文采用粒子群优化算法作为模型的求解工具，第2节提出的分段穿透罚函数用于处理第1节中模型的约束条件。粒子群规模为300，最大迭代次数为 4 000 次，r1=r2=2，ep1=1000，ep2=2500，穿透周期T′=100。其中，ep1的选取过小则容易破坏种群的多样性，选取过大则延长了算法的求解时间，ep2的选取应保证约束收敛段的长度不小于总长度的1／3，否则容易导致无法收敛于可行域内，同时应保证算法不在ep2前进入收敛。其他系数有：k1=0.2，k2=0.02，k′1=8／15，k3=20，k=0.1。 其具体的求解流程如图7 所示。

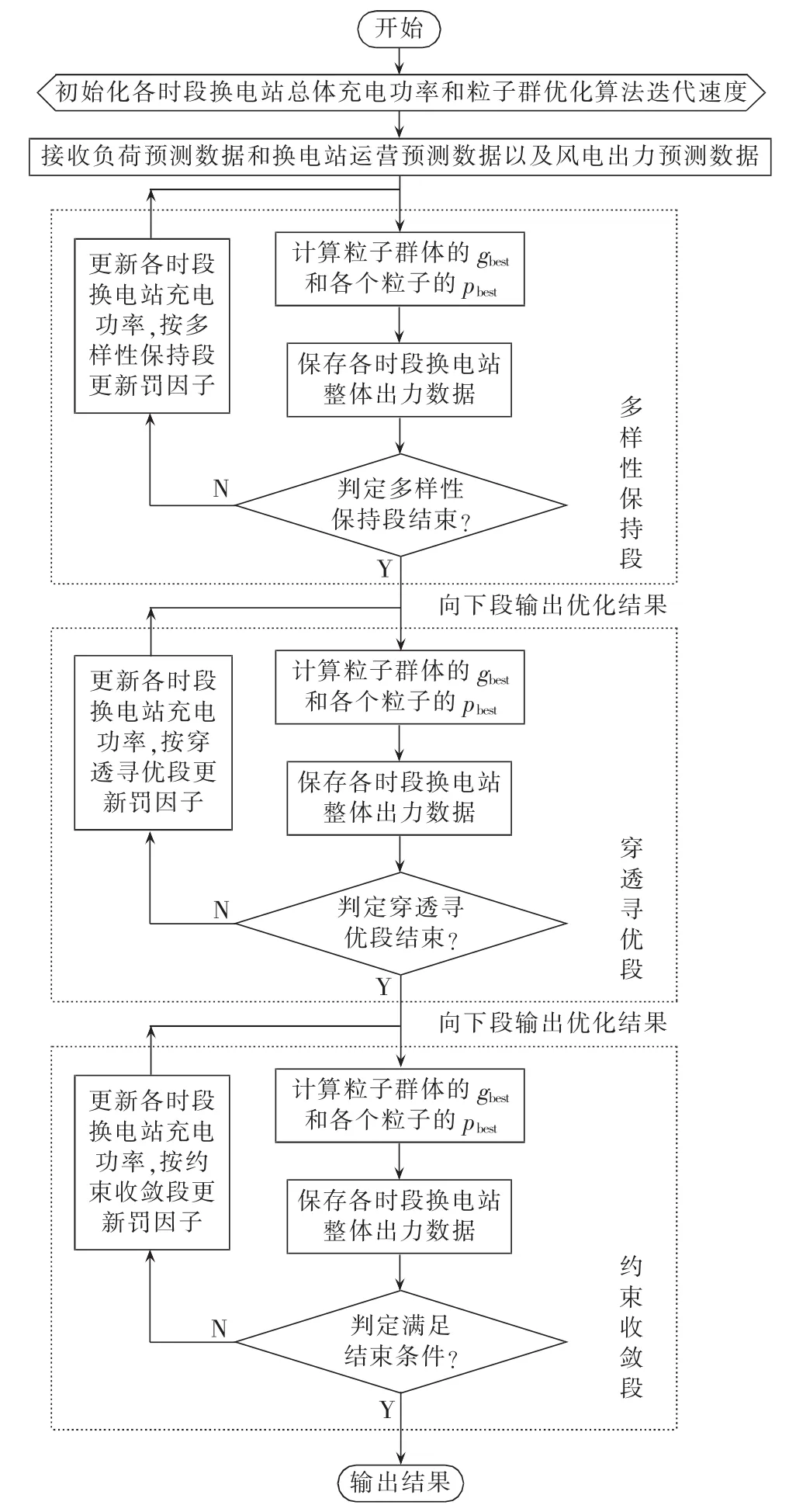
图7 求解流程图Fig.7 Flowchart of solution

对约束条件的设置，日总整体运营量Ppre.all.d取500 MW·h，并简化认为前日运营误差Pyestd.rev为0。假设配电网区域内的换电站最大电池储备容量均为30 MW·h，共有 5座，其中-20 MW≤PEi≤50 MW、Qimin=5 MW·h，PWi.max=50 MW，充放电效率取 β1=β2=0.9。对目标函数，因不同的电池具有不同的最佳电流和损耗代价，最佳充电电流下的功率统一简化取PbestN=20 MW，电池寿命损耗代价统一取a1=0.03、a2=0.005、b1=b2=0.07。 解得权重系数 λ1=0.17、λ2=0.66、λ3=0.17。最终目标函数即为：

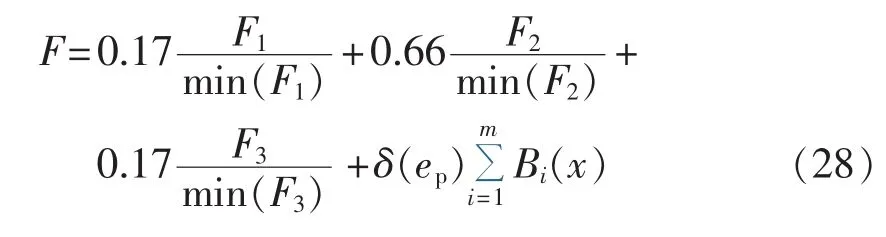
4 算例分析与验证

算例采用文献［19］中给出的日等效负荷变化曲线，如图8所示。可再生清洁能源为风电，采用文献［20］提供的风电机组出力数据，如图9所示（图中风电功率为标幺值），其中机组容量为50 MW。换电站的日运营曲线如图10所示，为更直观地展示优化结果，算例优化时间为12:00至次日12:00，各换电站的初始储备容量均为24 MW·h。分时电价如表1所示。

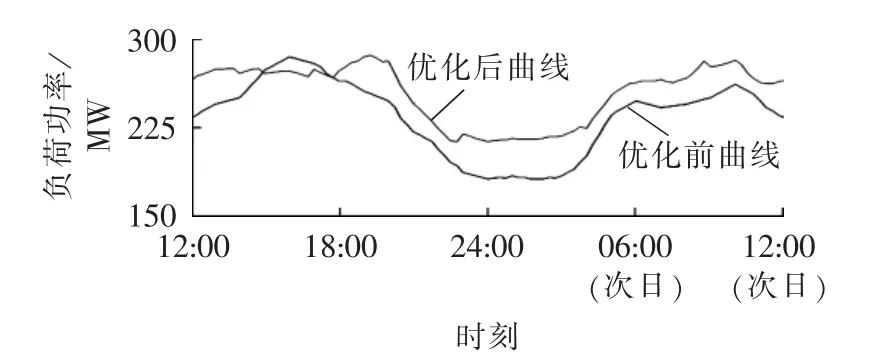
图8 优化前后负荷曲线Fig.8 Load curves，before and after optimization

图9 风电机组出力曲线Fig.9 Output power curve of wind turbine

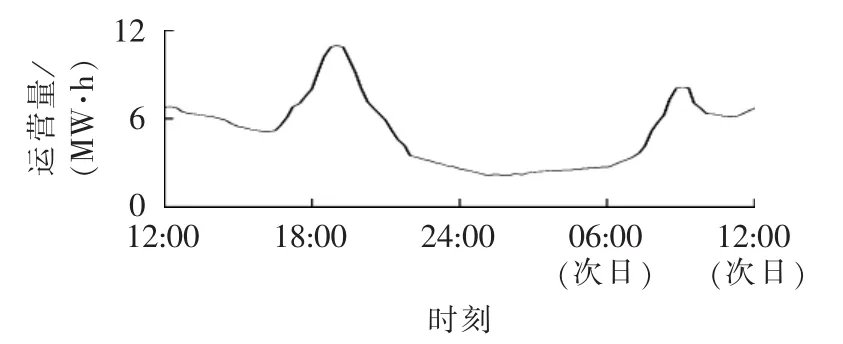
图10 电动汽车换电站运营预测曲线Fig.10 Predictive operational curve of EV battery swap station

表1 分时电价Table 1 Time-of-use electricity prices

优化后的日负荷曲线如图8所示，换电站整体出力情况如图11所示。对目标函数F1，电动汽车在负荷尖峰时反向放电，低谷期则大功率充电，换电站参与优化调度的情况下负荷曲线峰谷差降低了16.18%，负荷曲线更加平滑，起到了良好的削峰填谷作用。对目标函数F2，电动汽车能较好响应电网的分时电价，充分利用低价阶段充实库存，在高价阶段（如图11中15:00—17:00）则反向向电网售电获取经济收益，能有效降低换电站的运行费用。对目标函数F3，在风电出力较大的时段适当增加换电站的充电功率，提高清洁能源所占比例，对绿色出行有积极意义。同时，因采用了更为严格的约束条件，相对文献［21］的优化结果，换电站不仅在负荷低谷时有较大充电功率，而且在负荷尖峰和换电站运营尖峰到来前一段时间都需维持较大充电功率以保障换电站的可靠运营。

图11 电动汽车换电站整体充电出力曲线Fig.11 Total output power curve of EV battery swap station

图12为文献［7］给出的传统严格递增正序列罚函数和文献［11］提出的自适应罚函数以及本文提出的分段穿透罚函数的gbest曲线。该曲线结果为分别使用3种方法运行10次的平均值。各种算法的最终优化结果如表2所示。其中，传统递增罚函数算法寻优能力最差；自适应罚函数算法在前期具有极快的寻优速度，但同时也破坏了粒子的多样性，后期寻优能力差；分段穿透罚函数算法在前期保障了粒子的多样性，寻优速度明显慢于自适应罚函数算法，但在穿透效果的作用下在迭代1187次后就表现出比自适应罚函数算法更好的寻优效果。与其他罚函数处理方法gbest寻优曲线一直递减不同，穿透罚函数算法因等效变异带来的gbest迁移，会出现穿透尖峰，即后代的gbest值大于前代的现象。但这一现象并不影响粒子的总体寻优速度，等效变异往往有助于粒子更快在边界其他区域发现更优解。

图12 3种算法的gbest-ep曲线对比Fig.12 Comparison of gbest-epcurve among three algorithms

表2 3种算法的目标函数结果Table 2 Results of three objective function algorithms

5 结论

针对电动汽车换电站调度优化面临的高维、高约束问题，结合粒子群优化算法的原理特性，提出了分段穿透罚函数，包括优化多样性保持段罚函数、穿透寻优段罚函数、约束收敛段罚函数。对穿透罚函数的双向边界寻优特性、捷径寻优特性、等效变异特性进行了分析，并在MATLAB仿真平台上对文献［2］给出的传统严格递增正序列罚函数和文献［6］提出的自适应罚函数以及本文提出的分段穿透罚函数进行了算例对比验证，验证结果显示分段穿透罚函数具有良好的粒子多样性保持能力，对于约束优化问题有更强的边界寻优能力，同时寻优速度快，具有等效变异特性，能跳出局部最优解，增强了全局寻优能力。

可见，分段穿透罚函数能有效解决电动汽车换电站调度优化面临的高维、高约束问题，对电动汽车换电站的推广和提高、对间歇性电源的平抑效果有重要作用。同时，分段穿透罚函数还可应用于其他工程中类似的高维、高约束优化问题。其与更先进的改进算法，甚至其他类别的智能算法结合将可能获得更佳的寻优效果，将在后续研究中展示。

参考文献：

［1］赵俊华，文福拴，杨爱民，等.电动汽车对电力系统的影响及其调度与控制问题［J］.电力系统自动化，2011，35（14）：2-10.ZHAO Junhua，WEN Fushuan，YANG Aimin，et al.Impacts of electric vehicles on power systems as well as the associated dispatching and control problem［J］.Automation of Electric Power Systems，2011，35（14）：2-10.

［2］SORTOMME E，MOHAMMAD M H，JAMES M S D，et al.Coordinated charging of plug-in hybrid electric vehicles to minimize distribution system losses［J］.IEEE Transactions on Smart Grid，2011，2（1）：198-205.

［3］黄海丽.储能与风电协同利用对风电并网和碳排放的影响［D］.济南：山东大学，2012.HUANG Haili.Impact of energy storage and wind power synergistic dispatching on the wind power integration and CO2emission of power grid［D］.Ji’nan：Shandong University，2012.

［4］魏大钧，张承慧，孙波，等.基于分时电价的电动汽车充放电多目标优化调度［J］. 电网技术，2014，38（11）：2972-2977.WEI Dajun，ZHANG Chenghui，SUN Bo，et al.A time-of-use price based multi-objective optimal dispatching for charging and dispatching of electric vehicles［J］.Power System Technology，2014，38（11）：2972-2977.

［5］张齐东，黄学良，陈中，等.电动汽车电池更换站集群充电控制策略研究［J］. 电工技术学报，2015，30（12）：447-453.ZHANG Qidong，HUANG Xueliang，CHEN Zhong，et al.Research on control strategy for the uniform charging of electric vehicle battery swapping station［J］.Transactions of China Electrotechnical Society，2015，30（12）：447-453.

［6］刘文霞，赵天阳，邱威，等.规模化EV充电与风力／火电发电系统协调运行［J］. 电工技术学报，2013，28（5）：49-57.LIU Wenxia，ZHAO Tianyang，QIU Wei，et al.Coordinated operation of large scale electric vehicles charging with wind-thermal power system［J］.Transactions of China Electrotechnical Society，2013，28（5）：49-57.

［7］陈宝林.最优化理论与算法［M］.北京：清华大学出版社，2005：394-413.

［8］PARSOPOULOS K E，VRAHATIS M N.Particle swarm optimization method for constrained optimization problem［J］.Frontiers in Artificial Intelligence&Applications，2002，76（1）：214-220.

［9］罗贤海，张仁宏，曹坤，等.改进遗传算法及其在齿轮传动优化设计中的应用［J］. 机械设计与研究，2006，22（2）：64-67.LUO Xianhai，ZHANG Renhong，CAO Kun，et al.An improved genetic algorithm and its application in optimization design of the gear transmissions［J］.Machine Design and Research，2006，22（2）：64-67.

［10］YU Ying，YU Xiaochun，LI Yongsheng.Novel discrete particle swarm optimization based on huge value penalty for solving engineering problem［J］.Chinese Journal of Mechanical Engineering，2009，22（3）：410-418.

［11］车林仙，程志红.工程约束优化的自适应罚函数混合离散差分进化算法［J］. 机械工程学报，2011，47（3）：141-151.CHE Linxian，CHENG Zhihong.Hybrid discrete differential evolution with a self-adaptive penalty function for constrained engineering optimization［J］.Journal of Mechanical Engineering，2011，47（3）：141-151.

［12］邓长虹，马庆，肖永，等.基于自学习迁移粒子群算法及高斯罚函数的无功优化方法［J］. 电网技术，2014，38（12）：3341-3346.DENG Changhong，MA Qing，XIAO Yong，et al.Reactive power optimization based on self-learning migration particle swarm optimization and Gaussian penalty function［J］.Power System Technology，2014，38（12）：3341-3346.

［13］张颖，容展鹏，张宇雄，等.基于微电网的电网需求响应研究［J］.电力系统保护与控制，2015，43（21）：20-26.ZHANG Ying，RONG Zhanpeng，ZHANG Yuxiong，et al.Study of grid demand response based on micro grid［J］.Power System Protection and Control，2015，43（21）：20-26.

［14］刘梦璇，王成山，郭力，等.基于多目标的独立微电网优化设计方法［J］. 电力系统自动化，2012，36（17）：34-39.LIU Mengxuan，WANG Chengshan，GUO Li，et al.An optimal design method of multi-objective based island microgrid ［J］.Automation of Electric Power Systems，2012，36（17）：34-39.

［15］程浩忠.电力系统规划［M］.北京：中国电力出版社，2008：231-289.

［16］崔鹏程，陈明榜，向铁元.基于粒子群优化算法与混合罚函数法的最优潮流计算［J］. 电网技术，2006，30（增刊）：191-194.CUI Pengcheng，CHEN Mingbang，XIANG Tieyuan.Optimal power flow by particle swarm optimization and multi-SUMT method［J］.Power System Technology，2006，30（Supplement）：191-194.

［17］纪震，廖惠连，吴青华.粒子群算法及应用［M］.北京：科学出版社，2009：16-19.

［18］吕振肃，侯志荣.自适应变异的粒子群优化算法［J］.电子学报，2004，32（3）：416-420.LÜ Zhensu，HOU Zhirong.Particle swarm optimization with adaptive mutatio［J］.Acta Electronica Sinica，2004，32（3）：416-420.

［19］姚伟锋，赵俊华，文福拴，等.基于双层优化的电动汽车充放电调度策略［J］. 电力系统自动化，2012，36（11）：30-37.YAO Weifeng，ZHAO Junhua，WEN Fushuan，et al.Electric vehicle charging and discharging scheduling strategy based on bilevel optimization ［J］.Automation of Electric Power Systems，2012，36（11）：30-37.

［20］石庆均，耿光超，江全元.独立运行模式下的微网实时能量优化调度［J］. 中国电机工程学报，2012，32（16）：26-35.SHI Qingjun，GENG Guangchao，JIANG Quanyuan.Real-time optimal energy dispatch of standalone microgrid［J］.Proceedings of the CSEE，2012，32（16）：26-35.

［21］田文奇，和敬涵，姜久春，等.基于自适应变异粒子群算法的电动汽车换电池站充电调度多目标优化［J］.电网技术，2012，36（11）：25-29.TIAN Wenqi，HE Jinghan，JIANG Jiuchun，et al.Multi-objective optimization of charging dispatching for electric vehicle battery swapping station based on adaptive mutation particle swarm optimization［J］.Power System Technology，2012，36（11）：25-29.