基于改进贪心算法的大规模电动汽车充电行为优化
陈静鹏,朴龙健,艾 芊
(上海交通大学 电子信息与电气工程学院,上海 200240)
0 引言
电动汽车EV(Electric Vehicle)具有清洁环保、高效节能的优点,不仅能缓解化石能源危机,而且能够有效地减少温室气体的排放。2015年10月,国务院发布加快EV充电基础设施建设的指导意见,指出到2020年充电基础设施能满足500万辆EV充电需求[1],预计未来几年我国EV的保有量将大幅增长。然而,规模化EV的无序充电会加大电网负荷的峰谷差,并对电力系统的规划、配电网的电能质量和经济运行以及稳定性带来显著的影响[2-3]。反之,对EV的充电行为进行有序优化控制,充分发挥EV作为分布式储能元件的优势,能够实现削峰填谷、平抑可再生能源出力波动的功能,并为电网提供调峰、调频等辅助服务[4-7]。
目前,在集中控制方式下,有序充电控制策略大多都是运用 0-1整数规划方法进行求解[8-10]。0-1整数规划问题为非多项式(NP)算法问题,随着决策变量规模的扩大,计算复杂程度将以指数形式上升。当EV的数量达到一定规模时,充电站的优化计算时间将非常可观,影响充电控制的实时性。因此,集中控制方式下运用0-1整数规划方法只适用于对小规模的EV进行充电协调控制。
对于大规模EV的充电优化,目前的求解方法主要有启发式算法或分层、分布式的控制方式等。文献[11]中的启发式算法由于采用局部优化的策略,不能得到问题的最优解。文献[12-13]采用基于多代理系统的分布式控制方式实现EV充电负荷的协调控制。文献[12]由于中间管理者调控下的充电负荷与上层优化控制结果存在偏差,同样也无法实现对充电负荷的最优经济控制;文献[13]未考虑EV智能体行为的复杂性,实际操作时可能会由于智能体行为的随机性而无法实现预期的优化目标。
另一方面,大规模EV的充电行为将呈现更大的随机性,不仅会增加优化计算的复杂度,还会引发配电变压器容量越限、配电网负荷节点电压跌落和线路容量过载等问题,无法满足供电需求。而节点电压和线路容量约束具有非线性、多维度的特点,与配电网中的潮流分布相关,将其纳入配电网安全控制模型中会进一步提高大规模EV充电控制的难度,文献[8-13]均未考虑节点电压和线路容量约束。
针对以上问题,本文提出考虑节点电压和线路容量约束的大规模EV充电优化模型,并采用改进贪心算法进行求解。通过设计合理的贪心策略,克服了贪心算法容易陷入局部最优的缺陷。利用贪心算法的灵活性,提出对节点电压和线路容量分时段控制的配电网安全控制策略,迭代求解满足约束的充电站容量上限,降低了问题求解的难度。最后以IEEE 33节点配电测试系统为例,验证了所提控制策略和改进贪心算法对于大规模EV充电优化的有效性。
1 大规模EV的充电管理框架
图1为大规模EV分散接入配电网的场景示意图。EV的管理框架分为配电网代理商、本地代理商和EV 3个层次。配电网代理商分布在高中压HV/MV(High Voltage/Medium Voltage)变电层中,负责配电网的安全稳定控制以及EV的有序协调控制;本地代理商分布在中低压MV/LV(Medium Voltage/Low Voltage)变电层中,负责区域EV充电负荷的管控。充电站连接在配电变压器下,配电变压器下除了EV负荷EVL(EV Load)外,还有常规的居民负荷RL(Residential Load)。

图1 EV分层管理框架Fig.1 Framework of hierarchical EVs management
EV进入充电站后,充电智能终端可以获取电池的总容量、荷电状态SOC(State Of Charge)等信息,并通过以太网或专用无线网络提交给本地代理商;用户设置取车时刻以及充电预期荷电状态,充电结束后按实际充电电量向本地代理商支付费用。本地代理商将EV的状态信息和电量需求信息汇集后上传给配电网代理商。配电网代理商采取分时段实时滚动优化的控制策略,当有新的EV接入电网时,更新EV的充电需求信息,执行优化控制算法,并将充电计划分区下达给各个本地代理商,由本地代理商执行对管控区域内EV的充电控制。
2 EV充电优化模型
2.1 单台EV充电需求模型
EV到达充电站后,希望在离开时刻蓄电池能够达到期望的荷电状态,充电过程如式(1)所示,式(2)为电池容量约束。

其中,SOC(t)为t时段EV蓄电池的荷电状态;ut为t时段EV的充电状态,ut=1表示EV处于充电状态,ut=0表示EV处于空闲状态;Pc为EV充电功率;Δt为控制时间段长度;B为蓄电池容量;SOCE为EV期望的电池荷电状态;TD为EV的离开时刻。
2.2 配电网安全控制模型
为了确保配电网的安全运行,配电网代理商对EV的充电负荷进行协调控制,约束条件如下。
(1)节点功率平衡约束。

其中,j为与节点 i存在相连支路的节点;Pi、Qi、Ui分别为节点i的注入有功功率、无功功率、电压幅值;Gij、Bij分别为互导纳的实部和虚部;θij为支路的首、末端电压相角差。
(2)节点电压约束。

其中,Umin为节点电压下限;Umax为节点电压上限。
(3)线路容量约束。

其中,Sijmax为连接节点i、j的支路容量Sij的上限。
(4)配电变压器容量约束。

其中分别为 t时段区域 i的配电变压器总功率、常规负荷功率、充电功率和充电功率上限;Si、ρi、cosψi分别为区域配电变压器的额定容量、效率和功率因数。
2.3 优化目标函数
无序充电是指EV到达充电站后立刻开始充电,直到最大期望电量时停止。无序充电不仅经济效益低,而且会加大电网的负荷峰谷差。为了解决无序充电带来的问题,配电网代理商的优化控制目标函数如下。
(1)本地代理商收益最大化。

其中,utn为t时段充电站内第n辆EV的充电状态,为优化模型的控制变量;pt、ct分别为t时段本地代理商向电网的购电电费和向EV收取的充电电费;Δt为一个时间段的长度,Δt=15 min;N为充电站内EV数量;Tmax为一个充电站内所有EV的最大停留时间段,可表示为式(8)所示。

其中,TDn为第n辆EV的离开时刻;T为当前时刻表示不大于x的最大整数。
(2)配电变压器负荷峰谷差最小化。

(3)兼顾本地代理商收益最大化和配电变压器负荷峰谷差最小化的多目标优化。

优化计算时,以式(7)为首要优化目标,在满足本地代理商收益最大化的基础上,兼顾式(9)的优化目标,对配电变压器负荷峰谷差进行优化。
3 改进贪心算法求解
贪心算法来源于0-1背包问题,具有时间复杂度低、计算效率高、易于实现的优点,但是容易陷入局部最优[14]。贪心算法已经被广泛应用在电力系统的故障诊断[14]、负荷恢复优化[15]、网络重构[16]等领域。EV的充电优化模型是一个0-1整数规划问题,同样可以运用贪心算法进行求解。并且,通过对贪心算法进行改进,可以避免算法陷入局部最优,从而获得问题的最优解。
3.1 本地代理商收益最大化的改进贪心算法
本地代理商收益最大化的改进贪心算法流程如图2所示。代理商收益主要与充电时段的电费差ct-pt和EV的充电量相关,贪心算法的策略是:在满足式(6)的约束条件下使EV在ct-pt最大的时段充电,在满足式(2)的约束条件下最大化EV的充电量。优化流程中,当式(6)的约束不成立时,将 SOC(TD)-SOCE最大化且将充电状态的EV置为空闲状态,有利于满足式(2)的约束,最大化EV充电量;当式(2)约束不成立时,优先减少ct-pt最小时段的充电负荷。
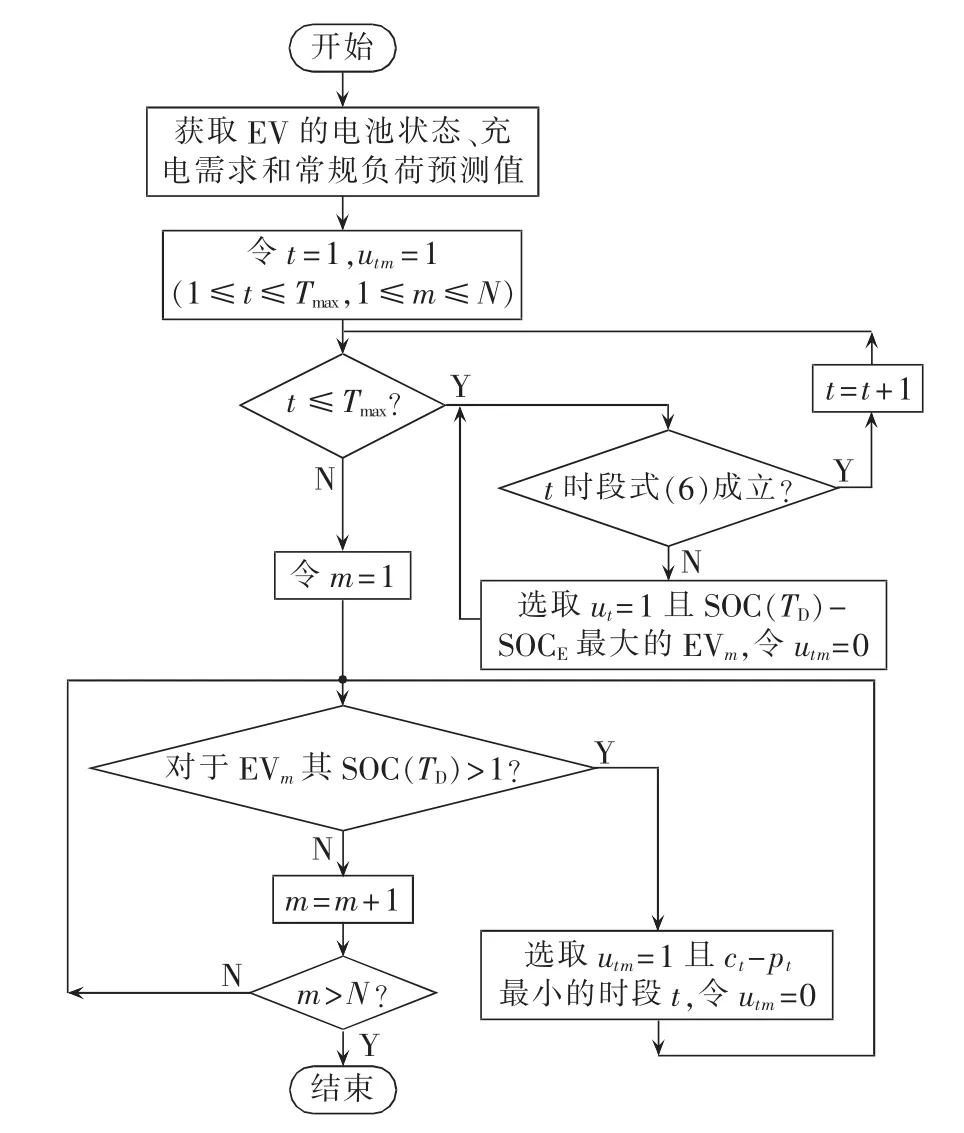
图2 本地代理商收益最大化的改进贪心算法流程图Fig.2 Flowchart of improved greedy algorithm for maximizing benefit of local agents
3.2 配电变压器负荷峰谷差最小化的改进贪心算法
配电变压器负荷峰谷差最小化的改进贪心算法流程如图3所示。贪心算法的策略是:在满足式(2)的约束条件下,循环地减小变压器负荷最大时段的充电负荷,以减小负荷的峰谷差。

图3 配电变压器负荷峰谷差最小化的改进贪心算法流程图Fig.3 Flowchart of improved greedy algorithm for minimizing peak-valley difference of distribution transformer
3.3 多目标优化的改进贪心算法
多目标优化有本地代理商收益最大化和配电变压器负荷峰谷差最小化2个目标函数。本文采取二次贪心算法进行求解,即在满足本地代理商收益最大化的基础上,进行配电变压器负荷峰谷差最小化的优化,算法流程如图4所示。贪心算法的策略是:在具有相同充电收益的时间段之间进行充电负荷的调整,能够在不降低本地代理商收益的前提下,减小配电变压器的负荷峰谷差。
3.4 配电网安全控制策略
在配电网安全控制模型中,主要有节点电压、线路容量、配电变压器容量3个不等式约束。贪心算法中将配电变压器容量减去常规居民负荷,转化为充电站功率上限 PmaxEi,t,如式(6)所示。
在同一配电网中,每个充电站负责为一片区域的EV提供充电服务。充电负荷增大会造成节点电压幅值下降或线路容量越限。配电网安全控制策略的思路是:当配电网某个区域出现节点电压或线路容量越限时,优先减少该区域充电站的功率上限PmaxEi,t;为了尽可能地满足EV的充电需求,分时段迭代求解充电站的最大功率上限,直到满足节点电压和线路容量约束为止。
配电网安全控制策略的具体流程如图5所示。

图4 多目标优化的改进贪心算法流程图Fig.4 Flowchart of improved greedy algorithm for multi-objective optimization

图5 配电网安全控制策略流程图Fig.5 Flowchart of distribution network security control
4 算例及结果分析
4.1 仿真参数设置
本文以IEEE 33节点配电网系统为例来验证改进贪心算法对于大规模EV充电优化的有效性,假设该系统为一条城市配线,共929户居民[17]。该配电网拓扑如图6所示,选取基准功率100 MV·A,基准电压12.66 kV,节点1为平衡节点,其他节点均为PQ节点,负荷节点的最低电压要求为0.95 p.u.。该配电网分为 3 个区域(A1,A2,A3),每个区域各有一个EV充电站,充电站分别接入节点3、13、30。EV的渗透率约为50%,共有450辆EV,均匀地分布在3个区域,各节点的日负荷数据引自文献[18]。算法采用MATLAB语言实现,在中央处理器为Intel Core i5、4 GB内存的计算机上完成仿真。
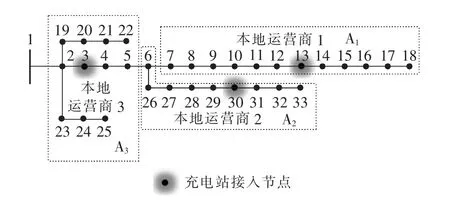
图6 IEEE 33节点系统网络拓扑图Fig.6 Network topology of IEEE 33-bus system
根据目前EV的发展状况,仿真情景设置如下。
a.EV电池容量为32kW·h,充电功率Pc为7kW,EV行驶100 km耗电量为15 kW·h。
b.配电变压器的容量为960 kV·A,负荷平均功率因数为0.85、效率为0.95,变压器的有功功率上限为 PTM=960×0.85×0.95=775.2(kW)。
c.本文的研究场景为居民区充电站为家用电动汽车提供充电服务。2009年,美国交通部对全美家用车辆的出行进行统计[19],结果表明,车辆的返回时刻、出行时刻服从正态分布,日行驶里程服从对数正态分布,其概率密度函数 fs(x)、fe(x)、fm(x)分别如式(11)—(13)所示。

其中,μs=17.47,σs=3.41;μe=8.92,σe=3.24;μm=2.98,σm=1.14。
d.用户设置的SOCE为0.9。
e.电网电价采用国内工业用电分时电价,充电电价采用统一电价[8]。
4.2 算法分析与对比
4.2.1 贪心算法与0-1整数规划算法对比
为了说明改进贪心算法的有效性,基于4.1节的算例实现文献[8]中的0-1整数规划优化算法。由于0-1整数规划只适用于求解不含节点电压和线路容量约束的小规模EV充电优化问题,下面主要针对本地代理商2的管控区域进行仿真,暂不考虑节点电压和线路容量约束。
以本地代理商收益最大化为目标,分别统计各个EV规模下不同优化算法一个时间段的平均计算时间和本地代理商1 d的运营收益。贪心算法是指图2所示的算法流程中,当式(6)的约束不成立时,随机将处于充电状态的EV置为空闲状态。仿真时,不同算法输入的EV需求数据相同,仿真结果如图7所示。

图7 不同算法的计算时间及本地代理商收益Fig.7 Computing time and benefit of local agents for different algorithms
从图7可以看出,在仿真的EV数量范围内,0-1整数规划算法的计算时间为数秒到数十秒,贪心算法和改进贪心算法的计算时间接近,仅为数毫秒,远小于0-1整数规划算法。当EV超过120辆时,贪心算法和改进贪心算法的计算效率比0-1整数规划算法高1000倍以上。并且,随着EV数量的增加,贪心算法和改进贪心算法的计算时间基本呈线性增长,而0-1整数规划方法呈指数型增长趋势。当EV的数量进一步增加时,0-1整数规划算法的计算时间将非常可观,因此不适用于大规模EV的充电优化问题;而贪心算法和改进贪心算法计算时间与EV规模呈线性关系,并且具有较高的计算效率,因此适用于大规模EV的优化问题。
优化结果方面,采用改进贪心算法的本地代理商收益和0-1整数规划算法相同,均能达到最优,高于贪心算法优化后的收益。可见,改进贪心算法很好地克服了贪心算法的缺陷,能够实现EV的最优充电控制。3种算法的性能比较见表1。
4.2.2 不同优化目标的改进贪心算法对比
为了比较不同优化目标的改进贪心算法效益,运用同一算例对不同优化目标的情景进行仿真,各情景下的负荷曲线如图8所示,效益对比如表2所示。该算例中,EV的数量为100辆,常规居民负荷的峰谷差为240 kW。

表1 不同算法的性能Table 1 Performances of different algorithms

图8 不同优化目标的负荷曲线Fig.8 Load curve for different optimization objectives

表2 基于改进贪心算法的不同优化目标的结果对比Table 2 Comparison of optimization based on improved greedy algorithm among different optimization objectives
从仿真结果可以看出,改进贪心算法能够针对不同的目标函数进行优化,提高本地代理商收益,降低配电变压器负荷峰谷差,并且计算效率都比较高,多目标优化由于采用二次贪心算法,计算时间虽然稍长,但仍能控制在毫秒级别,具有较快的实时响应能力。
4.3 配电网安全控制策略仿真分析
为了验证配电网安全控制策略的有效性,本文采用如图6所示的IEEE 33节点系统算例在2种不同的情景下进行仿真。配电网代理商对3个区域内的450辆EV进行充电优化,优化目标为本地代理商收益最大化,配电网安全控制策略中s=5,2种仿真情景设置如下。
情景1:配电网安全控制模型中不考虑负荷节点电压约束。
情景2:配电网安全控制模型中包含负荷节点电压约束。
不同情景下区域A1、A2、A3的EV充电负荷曲线和配电网末端节点 18(N18)、节点 33(N33)的电压幅值曲线如图9所示(图中电压为标幺值)。
由图9可见,情景1中各充电站的充电负荷主要集中在00:00—04:00时间段,从情景1的节点电压幅值曲线可以看出,过大的充电负荷会造成这些时间段N18和N33的电压幅值低于0.95 p.u.,严重影响配电网的电能质量。

图9 大规模EV充电优化仿真结果Fig.9 Simulative results of EVs charging optimization
情景2中考虑节点电压约束,对比不同情景下区域A1、A2的充电负荷曲线可以看出,相对于情景1,情景2中00:00—04:00时间段的部分充电负荷转移到了节点电压安全裕度较高的04:00—08:00和21:00—24:00时间段,由于区域A3处于配电网前端,无节点电压越限,因此情景1、2中区域A3充电负荷曲线相同。从情景2的节点电压幅值曲线可以看出,配电网末端节点电压均大于0.95 p.u.,因此各个区域的负荷节点电压幅值均能满足供电要求,说明了配电网安全控制策略的有效性。
进一步对情景2下不同优化目标的大规模EV充电优化进行仿真,仿真结果如表3所示。从表3可看出,不同优化目标下的充电负荷均能满足配电网安全约束。在计算时间方面,多目标优化已达到秒级别,配电变压器负荷峰谷差最小化仅为33.6 ms。因此,在对实时响应能力要求比较高的情况下,可以优先采用配电变压器负荷峰谷差最小化的优化控制目标。

表3 不同优化目标的大规模EV充电优化结果对比Table 3 Comparison of EVs charging optimization among different optimization objectives
5 结论
针对0-1整数规划算法求解效率低以及充电负荷使节点电压下降等问题,本文提出了基于改进贪心算法的大规模EV充电优化策略和考虑节点电压和线路容量约束的配电网安全控制策略。通过对算例结果的分析,得出以下结论。
a.改进贪心算法不仅具有较高的计算效率,而且能够克服贪心算法容易陷入局部最优的缺点,得到问题的最优解。随着EV数量的增加,改进贪心算法的时间复杂度呈线性增长,不会引发“维数灾”,适用于大规模EV的充电行为优化。
b.考虑节点电压约束的配电网安全控制策略能够确保节点电压幅值满足供电要求,减少充电负荷对电能质量的影响。
c.当节点电压安全裕度比较小时,多目标优化的计算效率比较低,可能会影响充电控制的实时性。以配电变压器负荷峰谷差最小化为目标时具有较高的计算效率,适用于对实时响应能力要求比较高的场合。
本文中假设EV为恒功率充电,并且未考虑EV的放电功能,下一步将研究运用改进贪心算法,在充放电功率可调的情形下对EV充放电负荷进行优化控制。
参考文献:
[1]国务院办公厅.国务院办公厅关于加快电动汽车充电基础设施建设的指导意见[EB/OL].(2015-10-09)[2015-10-22].http:∥www.gov.cn /zhengce/content/2015-10 /09 /content_10214.htm.
[2]郭建龙,文福拴.电动汽车充电对电力系统的影响及其对策[J].电力自动化设备,2015,35(6):1-9,30.GUO Jianlong,WEN Fushuan.Impact of electric vehicle charging on power system and relevant countermeasures[J].Electric Power Automation Equipment,2015,35(6):1-9,30.
[3]周念成,熊希聪,王强钢.多种类型电动汽车接入配电网的充电负荷概率模拟[J].电力自动化设备,2014,34(2):1-7.ZHOU Niancheng,XIONG Xicong,WANG Qianggang.Simulation ofcharging load probability for connection of different electric vehicles to distribution network[J].Electric Power Automation Equipment,2014,34(2):1-7.
[4]施泉生,平宗飞,陈敏骏.计及电动汽车入网的电价联动模型[J].电力自动化设备,2014,34(11):34-40.SHI Quansheng,PING Zongfei,CHEN Minjun.Electricity price linkage model considering V2G[J].Electric Power Automation Equipment,2014,34(11):34-40.
[5]SORTOMME E,EL-SHARKAWI M.Optimal scheduling of vehicleto-grid energy and ancillary services[J].IEEE Transactions on Smart Grid,2012,3(1):351-359.
[6]ANSARI M,AL-AWAMI A T,SORTOMME E,et al.Coordinated bidding of ancillary services for vehicle-to-grid using fuzzy optimization[J].IEEE Transactions on Smart Grid,2015,6(1):261-270.
[7]HAN S,HAN S,SEZAKI K.Development of an optimal vehicle-togrid aggregator for frequency regulation[J].IEEE Transactions on Smart Grid,2010,1(1):65-72.
[8]徐智威,胡泽春,宋永华,等.充电站内电动汽车有序充电策略[J].电力系统自动化,2012,36(11):38-43.XU Zhiwei,HU Zechun,SONG Yonghua,et al.Coordinated charging of plug-in electric vehicles in charging stations[J].Automation of Electric Power Systems,2012,36(11):38-43.
[9]张良,严正,冯冬涵,等.采用两阶段优化模型的电动汽车充电站内有序充电策略[J].电网技术,2014,38(4):967-973.ZHANG Liang,YAN Zheng,FENG Donghan,et al.Two-stage optimization model based coordinated charging for EV charging station[J].Power System Technology,2014,38(4):967-973.
[10]王岱,管晓宏,吴江,等.基于车辆行驶行为特性建模的电动汽车充放电策略与分析[J].电网技术,2014,38(9):2322-2327.WANG Dai,GUAN Xiaohong,WU Jiang,et al.Vehicle driving pattern based modeling and analysis of centralized charging/discharging strategy for plug-in electric vehicles[J].Power System Technology,2014,38(9):2322-2327.
[11]徐智威,胡泽春,宋永华,等.基于动态分时电价的电动汽车充电站有序充电策略[J].中国电机工程学报,2014,34(22):3638-3646.XU Zhiwei,HU Zechun,SONG Yonghua,et al.Coordinated charging strategy for PEV charging stations based on dynamic time-of-use tariffs[J].Proceedings of the CSEE,2014,34(22):3638-3646.
[12]王建,吴奎华,刘志珍,等.电动汽车充电对配电网负荷的影响及有序控制研究[J].电力自动化设备,2013,33(8):47-52.WANG Jian,WU Kuihua,LIU Zhizhen,et al.Impact of electric vehicle charging on distribution network load and coordinated control[J].Electric Power Automation Equipment,2013,33(8):47-52.
[13]许少伦,严正,冯冬涵,等.基于多智能体的电动汽车充电协同控制策略[J].电力自动化设备,2014,34(11):7-13,21.XU Shaolun,YAN Zheng,FENG Donghan,etal.Cooperative charging control strategy of electric vehicles based on multi-agent[J].Electric Power Automation Equipment,2014,34(11):7-13,21.
[14]孙伟,李林川,卢庆聪,等.基于停电区域的电力系统故障诊断的一种新模型[J].电网技术,2004,28(5):30-34.SUN Wei,LI Linchuan,LU Qingcong,et al.A new method for power system fault diagnosis based on power supply interrupted region[J].Power System Technology,2004,28(5):30-34.
[15]于文鹏,刘东,翁嘉明.含分布式电源的配电网供电恢复模型及改进贪婪算法[J].电力系统自动化,2013,37(24):23-30.YU Wenpeng,LIU Dong,WENG Jiaming.A power restoring model for distribution network containing distributed generators and improved greedy algorithm[J].Automation of Electric Power Systems,2013,37(24):23-30.
[16]李军军,许波桅,甘世红,等.基于贪婪度表的DPSO求解舰船电力系统网络重构[J].电工技术学报,2011,26(5):146-151.LI Junjun,XU Bowei,GAN Shihong,et al.Discrete particle swarm optimization algorithm based on greed table for network reconfiguration of the shipboard power system[J].Transactions of China Electrotechnical Society,2011,26(5):146-151.
[17]杨秀菊,白晓清,李佩杰,等.电动汽车规模化接入配电网的充电优化[J].电力自动化设备,2015,35(6):31-36.YANG Xiuju,BAI Xiaoqing,LI Peijie,et al.Charging optimization of massive electric vehicles in distribution network[J].Electric Power Automation Equipment,2015,35(6):31-36.
[18]宋文.含分布式发电的配电网优化规划研究[D].济南:山东大学,2014.SONG Wen.Research on optimal planning of the distribution network with distributed generation[D].Ji’nan:Shandong University,2014.
[19]US Department of Transportation,Federal Highway Administration.2009 national household travel survey[EB /OL]. (2011-06-20)[2015-10-01].http:∥nhts.ornl.gov/2009 /pub /stt.pdf.

