基于相空间重构的大型变压器绕组松动的振动特征识别

周 宇 ，马宏忠 ，李 凯 ，许洪华 ，蒋本洲

（1.河海大学 能源与电气学院，江苏 南京 211100；2.国网江苏省电力公司 南京供电公司，江苏 南京 210019；3.南京立业电力变压器有限公司 电气试验站，江苏 南京 211800）

0 引言

变压器是电力传输的枢纽设备。运输、安装、短路电流冲击等会导致变压器绕组压紧力减小［1-2］，使得绕组松动［3］。绕组压紧力减小会减弱绕组的抗短路冲击能力，严重威胁着变压器的正常运行［4-6］。

变压器油箱振动是对绕组振动和铁芯振动等振动源的响应。研究表明：铁芯和绕组分别受到磁致伸缩力［7］和电动力的作用，产生的振动分别正比于电压的平方［8］和电流的平方［2］。 振动的传播介质为变压器油、固体构件等。振动传递至油箱表面的过程中，其幅值衰减［9］。绕组松动、匝间短路等会影响变压器振动信号，因此振动信号可以用于变压器故障诊断。目前，国内外可用于评估变压器绕组压紧状态的有效方法并不多［10-14］。文献［3］指出变压器振动幅值变化与固有频率有关。文献［13］深入研究了空载状况下油箱表面振动加速度幅值和绕组压紧力之间的关系，提出利用空载时油箱表面测点振动加速度信号随压紧力减小的变化检测绕组压紧状态。研究表明［1］，在短路情况下，预紧力减小时，器身上的振动有一个先减小，然后随预紧力进一步减小而增大的过程。文献［15］中的实验是在短路情况下进行的，实验电压较低而电流较大，所以振动源主要是绕组振动，在其后的分析中考察了振动信号与电流之间的线性关系以及绕组松动后振动的变化。

在对变压器振动信号进行时频域分析时会遇到频谱泄漏、噪声影响等问题。阻尼、刚度等参数难以准确测定，所以建立动力学模型也存在较大难度。相空间重构是根据有限的数据来重构吸引子以研究系统动力学的方法。绕组压紧状态影响着变压器绕组振动传递能力、变压器固有频率以及漏磁场分布等，进而影响振动。本文通过相空间重构方法分析振动信号，目的是识别松动状态下振动信号的相空间轨线特征，该特征可以体现绕组松动对振动信号的影响。本文设计短路实验的原因是：短路实验的振动源主要是绕组振动，而空载实验的振动源主要是铁芯振动，相对于铁芯振动，绕组振动是绕组压紧状态更加直接的反应；变压器运行电压在额定电压附近，而电流随负荷变化，因此运行中的变压器振动信号的影响因素主要是电流和绕组状态。

1 相空间重构

1.1 概念

相空间重构的基本思想是：系统中任一分量的演化都是由与之相互作用的其他分量所决定的，相关分量的信息隐含在任一分量的发展过程中，即用系统的一个观察量可以重构出原动力系统模型。文献［16］证明了可以找到一个合适的嵌入维数重构相空间，可以把相空间内有规律的轨迹（吸引子）恢复出来。

设有一时间序列｛xi｝（i=1，2，…，N0），对其重构的相空间Rm的元素为：

其中，m为重构相空间的维数；τ为延迟时间间隔数，为延迟时间与采样时间间隔之比；p=N0-（m-1）τ，为时间序列嵌入相空间的向量个数；N0为时间序列的数据点数。

1.2 重构参数的确定方法

由重构相空间理论［17-20］可知，选取合适的时间延迟τ和嵌入维数m是进行相空间重构的关键。

考虑到相图的可视性，选取m=2或3。被测的振动信号时间序列是有限长的信号并含有环境、仪器等产生的噪声，由Takens定理知，τ不能随意选取。一般根据经验来选择τ，其基本思想是使xj和xj＋τ具有某种程度的独立但又不完全无关，以便它们在重构相空间中作为独立的坐标处理。求取τ的方法有自相关函数法、平均位移法、复自相关法和互信息法［19-20］等。本文采用平均位移法。

在L2范数（指先求向量各元素的平方和然后求平方根）下定义平均位移S（m，τ）为：

平均位移S（m，τ）表示重构状态空间的轨线从状态空间主对角线打开的程度。当τ较小时，重构后的吸引子会被压缩在主对角线一带，而随着τ的增大，吸引子的形状会逐渐展开。最后求得的τ应该保证重构的相空间轨线从相空间的主对角线向外扩展，而又不发生折叠现象。文献［17］建议取S（m，τ）-τ曲线的斜率第一次减少到小于初始斜率40%时的τ为最佳延迟时间间隔。本文应用该方法时，求取最佳延迟时间间隔后进行了小范围的调整，以达到最佳的重构效果。

2 实验系统与实验方法

对南京立业电力变压器有限公司的一台110 kV变压器进行不同压紧状态下的短路实验，测取油箱表面的振动加速度信号。

2.1 实验系统

实验系统包括发电机、变压器、振动加速度传感器、采集仪和液压系统等。

a.发电机用于向变压器高压侧绕组提供50 Hz交流电。

b.变压器的型号为SFZ10-31500／110，联接组标号为YNd11，低压侧额定电压为10.5 kV，额定电流IN为1732 A。实验时，令变压器的低压侧绕组三相短路。

c.振动加速度传感器的型号为JF2020，其输出电压与振动加速度的对应关系为20 mV／g（g为重力加速度）。振动加速度传感器靠磁座吸附在变压器油箱表面。

d.采集仪选用Nicolet采集仪，采样频率设置为10 kHz，每次采样时间为10 s。由采集仪向振动加速度传感器施加2 mA激励。

e.液压系统可以通过油压泵精确控制绕组压紧力。

2.2 绕组压紧力设置方法

根据实验方案人为地对绕组压紧力大小进行设置。对变压器进行抽油、吊罩操作，然后通过液压系统控制绕组压紧力，实现绕组不同压紧状态的设置。设置过程为如下。

a.使用扳手拧松压紧螺母，然后将液压千斤顶放置在绕组和结构件之间；液压表显示液压千斤顶所受压力，28 MPa对应绕组未松动状态的额定压紧力，0 MPa对应松动状态的绕组压紧力。

b.控制液压，待压力稳定后，拧紧压紧螺母，使得液压千斤顶可以抽出；然后再将变压器罩恢复、注油。

针对设计的不同压紧力方案，每次均按上述过程进行抽油、吊罩、调整压紧力等操作。本实验共设置3种压紧状态：压紧（三相绕组压紧力均为28 MPa）、松动（三相绕组压紧力均为0 MPa）和B相半松状态（B相压紧力为14 MPa而其余相绕组压紧力为28 MPa）。在寻找绕组松动特征时，选取振动信号差别较大的压紧状态和松动状态下的振动信号进行分析，找出特征并制定绕组松动识别方法。然后利用B相半松状态的振动信号进行绕组松动识别方法的验证。

2.3 振动信号测量方法

图1为振动信号测点布置图，振动信号测点布置在图中的1、2、3号位置，位于变压器油箱顶面，测点正下方分别对应着C、B、A三相绕组。绕组和铁芯通过结构件与油箱底部相连，与油箱顶部紧密接触。同一实验条件（同一种压紧状态和同一种电流状态）下的实验数据测3次。电流状态有6种，分别为20%额定电流、40%额定电流、60%额定电流、80%额定电流、100%额定电流和110%额定电流。

3 振动信号相空间重构

首先对处于油箱顶部中间位置的2号测点的振动信号进行相空间重构：求取S（m，τ）-τ 曲线，并依据平均位移法求得最佳延迟时间，绘制不同电流状态和不同压紧状态下的相图。然后运用同样的方法分析1号测点和3号测点的振动信号。

3.1 振动信号相空间重构参数的确定

本文进行实验数据处理的目的是把相空间内有规律的轨迹恢复出来，通过相图识别绕组松动缺陷。重构参数m和τ的选取尤为关键，本文选取2号测点未松动时额定电流下的第1次测量振动信号进行计算，确定重构参数。本文取m=2，考察二维相图（相平面）。由式（2）计算振动信号的平均位移，绘制S（m，τ）-τ 折线图，如图2 所示。

图2 2号测点振动信号 S（m，τ）-τ 折线图Fig.2 Curve ofS（m，τ） vs.τ for vibration signal of measuring point No.2

根据平均位移法，计算初始斜率，当曲线斜率第一次下降到初始斜率的40%以下时，取对应的τ值为最佳延迟时间间隔。由图2可以看出在τ=20时曲线斜率约为0，所以最佳延迟时间间隔在20以内。为方便计算，运用MATLAB曲线拟合工具箱中的Fourier对延迟时间间隔在20以内的S（m，τ）-τ散点图进行拟合。拟合结果如图3所示。拟合曲线的解析式为：

其中，ω=0.09377。

图3S（m，τ）-τ 散点拟合Fig.3 Fitted curve ofS（m，τ） vs.τ

从x=1开始计算导数f′（x），由计算结果可知，使得 f′（x）／f′（1）＜40% 成立的第一个整数点为 x=10（f′（10）／f′（1）=38.12%）。 附近点的斜率与初始斜率的比值为：f′（9）／f′（1）=41.17%，f′（11）／f′（1）=34.1%。 MATLAB 显示结果为：R-square=0.9816，该值越接近1，表明拟合越理想；均方根误差（RMSE）为0.001318，较小。根据拟合曲线，求得最佳延迟时间间隔τ为10，因为采样频率是10 kHz，所以对应的延迟时间为 0.001 s。

3.2 振动信号相空间重构

将2号测点在不同电流状态和不同压紧状态下的振动信号按m=2和τ=10进行相空间重构，发现同一实验条件下3次测量振动信号得到的相平面几乎相同，本文取第1次测量结果进行分析，如图4所示（由于篇幅所限，第2次和第3次测量信号对应的相平面本文不再示出）。对于本文中的相空间重构，其主对角线是 y=x［22］。 图4（a）、（b）中，波形由上至下分别为 110%、100%、80%、60%、40%、20% 额定电流下的相平面，横轴为振动向量v（i），纵轴为振动向量v（i+τ）。为了防止图形随横纵坐标的比例而变化，将图4的横轴和纵轴的尺度比例设置成1∶1，下文的所有相图均采用该设置。

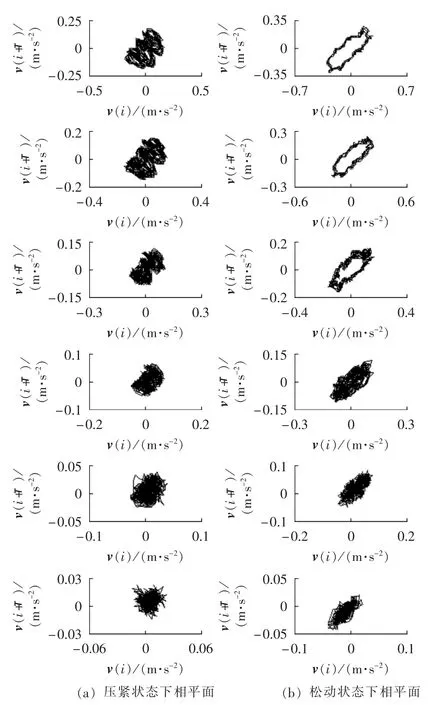
图4 2号点振动信号的延迟10相平面Fig.4 Phase planes of vibration signals of measuring point No.2 whenτ=10

从图4中可以得出以下结论。

a.松动状态和压紧状态下振动信号的相平面不同，这是因为绕组松动后影响了变压器绕组的振动传递能力、变压器固有频率以及漏磁场分布等，导致松动状态和压紧状态下的振动信号不同，其重构出的相平面也不相同。

b.观察松动状态下，电流为80%、100%、110%的额定电流时的相平面轨线，可以发现：轨线近似为空心椭圆形状，即每个相点均在空心椭圆上并且每个相点与下一个相点的连线也在空心椭圆上；振动信号重构得到的相平面轨线从空间主对角线打开，证明选取的维数和最佳延迟时间参数效果较好；压紧状态下的振动信号相平面轨线交叉混叠，未沿着主对角线打开。根据动力学理论［21］，系统振动所得相平面轨线的闭合性可以用于判断系统振动的周期性，轨线是否有畸变可以用于判定系统处于线性振动或非线性振动状态。相平面轨线是闭合的椭圆，表明变压器短路实验中的稳态振动是周期振动，其振动基频为100 Hz［2］；椭圆形状有畸变，表明变压器振动系统是非线性系统。非线性关系存在于磁感应强度与磁场强度之间以及电流与磁通之间。

c.观察20%、40%、60%的额定电流状态下的相平面可见，松动状态和压紧状态下的轨线均未沿着主对角线打开，2种状态下的相平面区分度不大。这是因为较小电流下，振动信号不强，随机性较大，信噪比小，容易受噪声影响，其振动信号与大电流下的振动信号差别较大，嵌入维数和最佳时间延迟由额定电流状态下的振动信号得到，运用该参数对较小电流状态下（60%及以下的额定电流）的振动信号进行相空间重构，并不能达到满意的效果。

因为所处位置均在顶面，所以1、3号测点的振动信号与2号测点振动信号存在一定的相似性。将由2号测点的振动信号得到的重构参数运用到1、3号测点振动信号的相空间重构中，发现重构效果并不理想，原因是2号测点振动信号与1号、3号测点的振动信号也存在一定的差异性，存在差异的原因是分接开关、储油罐等结构对3个测点的振动信号有不对称的影响。所以在τ=10附近寻找合适的时间延迟。首先进行初选：以10为中心，每隔5个时间延迟间隔确定1个延迟进行相空间重构；当呈现出有规律的轨线时，确定当前延迟为初选延迟。然后进行细选：以初选延迟为中心，每隔1个时间延迟间隔确定1个延迟进行相空间重构。如果采用某个延迟后，松动状态下1、3号测点的振动信号在尽可能多的电流状态下的相平面轨线可以沿主对角线打开而又尽量不发生折叠现象，则确定当前延迟为最佳时间延迟。最终得到1号测点的最佳时间延迟为τ=6，3号测点的最佳时间延迟为τ=16。同一实验条件下的3次测量振动信号得到的相平面几乎相同，取第1次测量结果进行分析。1、3号测点的振动信号相平面分别如图5、6所示，各波形与电流、压紧状态的对应关系与图4相同。限于篇幅，1号测点的第2次和第3次测量信号对应的相平面，以及3号测点的第2次和第3次测量信号对应的相平面本文不再示出。

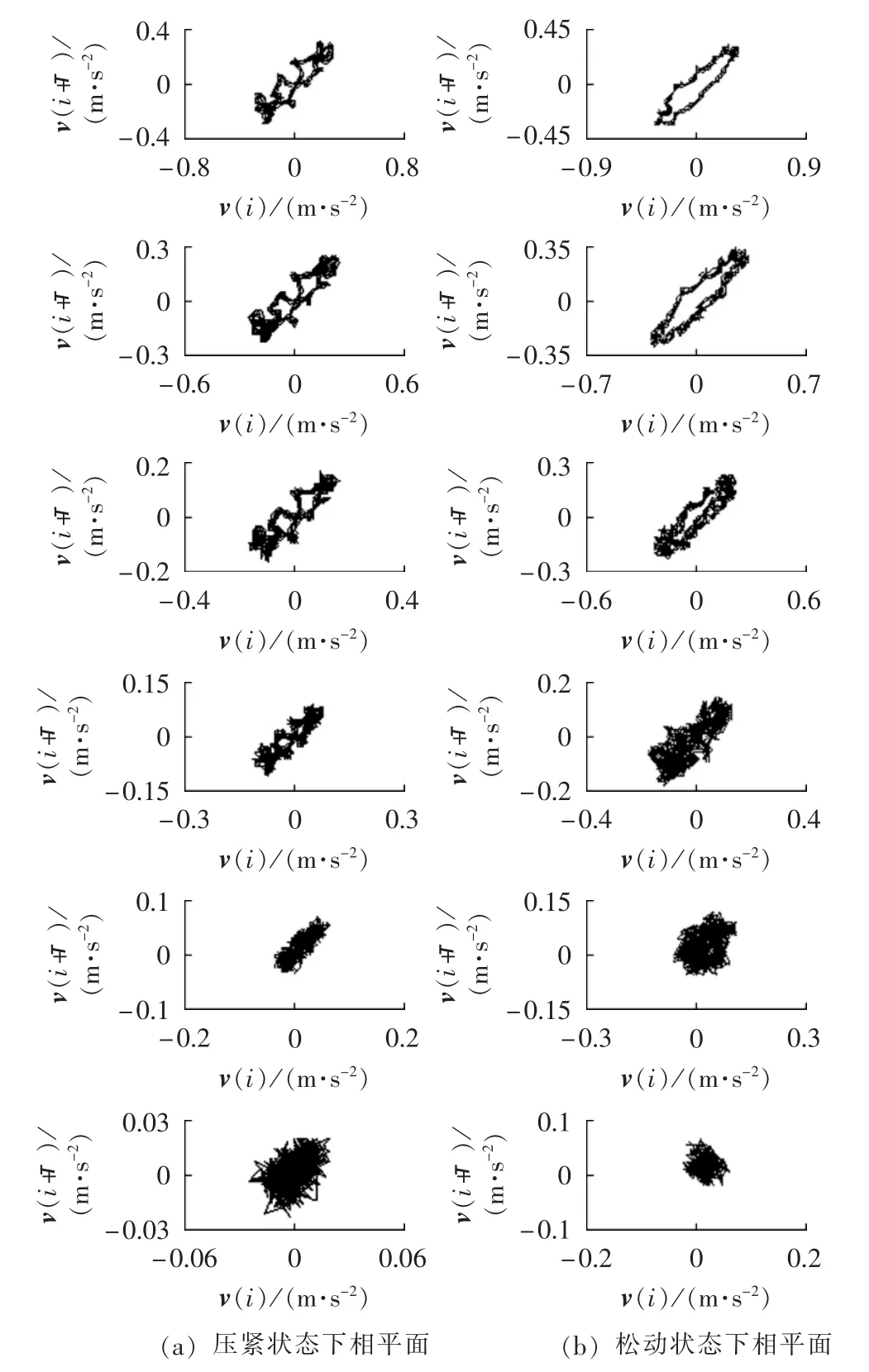
图5 1号点振动信号的延迟6相平面Fig.5 Phase planes of vibration signals of measuring point No.1 whenτ=6

按照对图4的分析方法，分析图5、6，分析结果如表1所示。

表1表明：对于在100%、110%额定电流状态下运行的变压器，可以通过测绘其顶面3个测点振动信号相平面，根据识别的松动状态相平面特征（轨线近似为空心椭圆），对绕组压紧状态进行判断；在80%、100%、110%额定电流状态下运行的变压器，可以通过测绘其顶面2号和3号测点振动信号相平面，判断绕组压紧状态。

4 应用振动信号相空间重构方法识别变压器绕组松动

4.1 方法内容

依据前文对差别较大的压紧状态和松动状态下振动信号的分析可知，能够根据相图特征识别变压器绕组松动，步骤如下。

a.寻找某种类型（容量相同且结构类似）变压器的绕组松动对应的相图特征。对该类型的某台变压器进行短路实验，测取油箱上表面的振动信号。为保证采集的信号中变压器振动信号是稳定的主要成分，电流应该设置为80%及以上的额定电流。

图6 3号点振动信号的延迟16相平面Fig.6 Phase planes of vibration signals of measuring point No.3 whenτ=16

表1 变压器油箱顶面3个测点相平面分析Table1 Analysis of phase planes for 3 measuring points

b.根据平均位移法求取最佳延迟时间，在小范围内调整最佳延迟时间，使得绘制出的松动状态下的振动信号2维或3维相图具有明显的特征。

c.根据发现的相图特征，监测同种类型的变压器是否存在绕组松动缺陷。若图形满足相图特征，则判断变压器存在绕组松动缺陷。

步骤a、b仅针对某一类型的变压器相空间特征的寻找过程，对不同类型的变压器应有不同的相图数据库。步骤c为变压器的监测过程。

对于与本文实验对象同类型的变压器，根据表1，在80%、100%、110%额定电流下运行的该类型变压器绕组松动的识别方法为：对于在100%、110%额定电流下运行的变压器，若其顶面1、2、3号测点的振动信号相平面近似为空心椭圆，则判定其存在绕组松动缺陷；对于在80%、100%、110%额定电流下运行的变压器，若其顶面2、3号测点的振动信号相平面近似为空心椭圆，则判定其存在绕组松动缺陷；若变压器顶面振动信号相平面未沿主对角线打开，未呈现出空心椭圆形状，则判定其不存在绕组松动缺陷。

4.2 方法验证

利用B相半松状态下的振动信号对绕组松动的识别方法进行验证。选用表1中的重构参数对B相半松状态下1、2、3号测点的振动信号进行相空间重构。在同一实验条件下测取3次振动信号，取第1次测量结果进行分析，见图7，图中从左至右分别对应110%、100%、80%额定电流。B相半松状态下1、2、3号测点第2次和第3次测量信号的相平面与第1次测量信号相平面几乎相同，限于篇幅，不再显示。

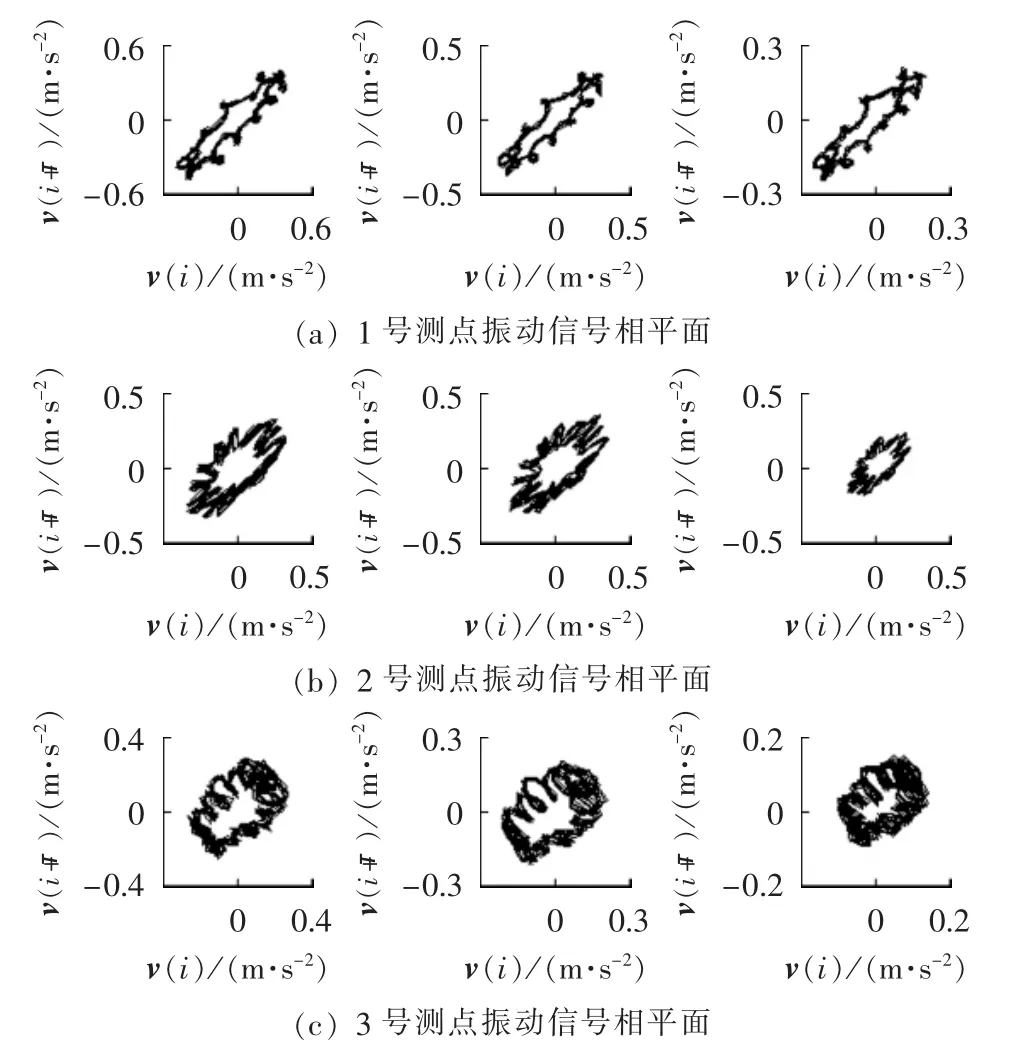
图7 B相半松状态下1—3号测点振动信号相平面Fig.7 Phase planes of vibration signals of 3 measuring points，when phase-B winding is half loosened

由图7可以得出以下结论。

a.1、2、3号测点的轨线在一定程度上有空心椭圆的形状，与图4（a）、图5（a）和图6（a）中的交叉混叠的绕组压紧状态轨线之间存在差异，可以判断测试变压器存在绕组松动缺陷。

b.2号测点相平面轨线沿主对角线打开的程度大于1、3号测点，原因是2号测点更靠近发生松动的B相绕组，其振动信号与压紧状态下振动信号的差别更大。根据这一特点可以进一步实现绕组松动相的定位。

c.对比图4（b）、图5（b）和图6（b）的绕组松动状态轨线和B相半松状态轨线（图7）可以发现，松动（三相绕组全部松动）状态轨线比半松动状态轨线的形状特征更加明显，畸变较小，这为进一步区分绕组松动程度提供了思路。

5 结论

绕组压紧状态影响着变压器绕组的振动传递能力、固有频率以及漏磁场分布，进而影响振动。绕组松动前后的振动信号重构相图的差异体现了绕组松动对振动信号的影响。

恰当地选取重构参数m和τ，可以把振动信号相空间内有规律的轨线恢复出来。结合试凑方法，应用平均位移法求取最佳时间延迟间隔。松动状态下，较大电流（80%、100%、110%额定电流）下的轨线为一闭合的空心畸变椭圆，这表明变压器振动是非线性周期振动。

本文中的实验变压器并未装载风扇，对于带风冷的变压器，其振动信号含有风扇振动成分，与本文测取的振动信号存在差异，需要重新选定重构参数。本文实验对象为钟罩式结构的大型变压器，而小型变压器（如10 kV变压器）为吊芯式结构，振动信号抗干扰能力较弱，其振动信号测点布置以及重构效果有待进一步研究。

参考文献：

［1］谢坡岸.振动分析法在电力变压器绕组状态监测中的应用研究［D］.上海：上海交通大学，2008.XIE Poan.Study on application of vibration analysis to the condition monitoring of power transformers windings［D］.Shanghai：Shanghai Jiao Tong University，2008.

［2］马宏忠，耿志慧，陈楷，等.基于振动的电力变压器绕组变形故障诊断新方法［J］.电力系统自动化，2013，37（8）：1-7.MA Hongzhong，GENG Zhihui，CHEN Kai，et al.A new fault diagnosismethod forpowertransformerwinding deformation based on vibration［J］.Automation of Electric Power Systems，2013，37（8）：1-7.

［3］陆瑾.应用机械振动法对变压器绕组状态进行在线测试的研究［D］.上海：上海交通大学，2008.LU Jin.The studyon the on-linediagnosisoftransformer winding status with the method of mechanical vibration［D］.Shanghai：Shanghai Jiao Tong University，2008.

［4］姚森敬，欧阳旭东，林春耀.电力变压器绕组变形诊断分析［J］.电力系统自动化，2005，29（18）：95-98.YAO Senjing，OUYANG Xudong，LIN Chunyao.Analysison winding deformation diagnosing of power transformers［J］.Automation of Electric Power Systems，2005，29（18）：95-98.

［5］马宏彬，何金良，陈青恒.500 kV单相电力变压器的振动与噪声波形分析［J］.高电压技术，2008，34（8）：1599-1604.MA Hongbin，HE Jinliang，CHEN Qingheng.Vibration and sound waveform analysis of 500 kV single phase power transformer［J］.High Voltage Engineering，2008，34（8）：1599-1604.

［6］刘军，张安红.电力变压器绕组短路动稳定能力的仿真和评估［J］.变压器，2012，49（6）：14-25.LIU Jun，ZHANG Anhong.Simulation and evaluation of short circuit dynamic stability of windings in power transformer［J］.Transformer，2012，49（6）：14-25.

［7］祝丽花，杨庆新，闫荣格，等.考虑磁致伸缩效应电力变压器振动噪声的研究［J］.电工技术学报，2013，28（4）：1-6.ZHU Lihua，YANG Qingxin，YAN Rongge，etal.Research on vibration and noise ofpowertransformer cores including magnetostriction effects［J］.Transaction of China Electrotechnical Society，2013，28（4）：1-6.

［8］马宏忠，赵宏飞，陈楷，等.基于振动的变压器铁芯松动判定方法［J］.电力系统自动化，2013，37（14）：101-106.MA Hongzhong，ZHAO Hongfei，CHEN Kai，etal.Determine method for transformer core looseness based on vibration ［J］.Automation of Electric Power Systems，2013，37（14）：101-106.

［9］沈培锋，赵宏飞，李凯，等.基于振动的变压器铁芯松动定位［J］.中国电力，2015，47（9）：66-70.SHEN Peifeng，ZHAO Hongfei，LI Kai，etal.Positioning of transformer core loosening based on the vibration signals ［J］.Electric Power，2015，47（9）：66-70.

［10］SANZ-BOBI M A，GARCIA-CERRADA A，PALACIOS R，et al.Experiences learned from the on-line internal monitoring of the behavior of a transformer［C］∥Proceedings of the IEEE International Electric Machines and Drives Conference Record.Milwaukee，WI，USA：IEEE，1997：TC3-11.1-TC3-11.3.

［11］GARCA B，BURGOS J C，ÁGEL A.Winding deformations detection in power transformers by tank vibrations monitoring［J］.Electric Power Systems Research，2005，74（1）：129-138.

［12］BERLER Z，GOLUBEV A，RUSOV V，et al.Vibro-acoustic of transformer clamping pressure monitoring［C］∥Conference Record of the 2000 IEEE International Symposium on Electrical Insulation.Anaheim，CA，USA：IEEE，2000：263-266.

［13］谢坡岸，金之俭，饶柱石，等.振动法检测空载变压器绕组的压紧状态［J］.高电压技术，2007，33（3）：188-189.XIE Poan，JIN Zhijian，RAO Zhushi，et al.Windings clamped state detected by vibration method on unloadeded transformer［J］.High Voltage Engineering，2007，33（3）：188-189.

［14］程锦，李延沐，汲胜昌，等.振动法在线监测变压器绕组及铁心状况［J］.高电压技术，2005，31（4）：43-48.CHENG Jin，LIYanmu，JIShengchang，etal.Application of vibration method on monitoring the winding and core condition of transformer［J］.High Voltage Engineering，2005，31（4）：43-48.

［15］赵宏飞，马宏忠，陈楷，等.基于振动信号的变压器绕组松动实验研究［J］.中国电力，2015，47（1）：13-16.ZHAO Hongfei，MA Hongzhong，CHEN Kai，et al.Experimental study oftransformerwinding loosenessbased on vibration signal［J］.Electric Power，2015，47（1）：13-16.

［16］TAKENS F.On the numerical determination of the dimension of an attractor［J］.Lecture Notes in Mathematics，1985，1125：99-106.

［17］ROSENSTEIN M T，COLLINS JJ，DE LUCA C J，etal.Reconstruction expansion as a geometry-based framework for choosing proper delay times［J］.Nonlinear Phenomena，1994，73（1-2）：82-98.

［18］顾洁.电力系统短期负荷预测方法研究［J］.电力自动化设备，2002，22（2）：20-22.GU Jie.Study on short-term load forecast method for power system［J］.Electric Power Automation Equipment，2002，22（2）：20-22.

［19］安学利，蒋东翔.风力发电机组运行状态的混沌特性识别及其趋势预测［J］.电力自动化设备，2010，30（3）：15-19，24.AN Xueli，JIANG Dongxiang.Chaotic characteristics identification and trend prediction of running state for wind turbine ［J］.Electric Power Automation Equipment，2010，30（3）：15-19，24.

［20］李慧杰，刘亚男，卫志农，等.基于相关向量机的短期风速预测模型［J］.电力自动化设备，2013，33（10）：28-32.LIHuijie，LIU Yanan，WEIZhinong，etal.Short-term wind speed forecasting model based on relevance vector machine［J］.Electric Power Automation Equipment，2013，33（10）：28-32.

［21］司马文霞，陈莉珺，杨庆，等.基于过电压时间序列的铁磁谐振在线建模与反馈控制［J］.高电压技术，2014，40（7）：1948-1956.SIMA Wenxia，CHEN Lijun，YANG Qing，et al.Online modeling and feedback control of ferroresonance based on overvoltage time series［J］.High Voltage Engineering，2014，40（7）：1948-1956.

［22］林嘉宇，黄芝平，王跃科，等.语音信号相空间重构中时间延迟选择的改进的平均位移法［J］.国防科技大学学报，1999，21（3）：59-62.LIN Jiayu，HUANG Zhiping，WANG Yueke，et al.Modification of average displacement method for selection of time-delay in phase space reconstruction of speech signals［J］.Journal of National University of Defense Technology，1999，21（3）：59-62.