考虑风电功率概率分布不确定性的含风电配电网无功规划方法

谢 俊 ，王 璐，傅旭华 ，边巧燕，辛焕海 ，甘德强

（1.南京邮电大学 自动化学院，江苏 南京 210023；2.国网浙江省电力公司，浙江 杭州 310007；3.浙江大学 电气工程学院，浙江 杭州 310027）

0 引言

近年来，以风电为代表的可再生能源迅速发展，在减轻环境污染以及缓解能源危机方面做出了较大贡献。然而风电具有间歇性、不确定性以及部分可预测性，给配电网的无功规划问题［1］带来较大挑战。

含风电的配电网无功规划运行是指在风速或风电功率预测的基础上，以有功网损和无功补偿设备投资成本之和最小为目标，实现对无功补偿设备安装地点和容量的优化决策［2］。

在已有的研究中，通常是假设风速或风电出力概率分布已知，采用概率解析法［2］、场景分析法［3-5］研究风电的不确定性对配电网无功规划的影响。文献［2，6-7］采用蒙特卡罗法抽样风电功率的概率密度函数求解风机的输出功率，进而进行配电网无功规划决策；文献［8-11］采用多场景分析技术模拟风机的出力，利用成本效益分析法建模并采用粒子群算法求解模型。

然而，由于风电预测技术的局限性［11-12］，以及气候、地形分布的多样性，很难准确描述风电的不确定性，只能获得风电概率分布的部分信息，如若干阶矩信息。常用来描述风电功率不确定性的概率分布有正态分布［13］、贝塔分布［14］、拉普拉斯分布［15］以及柯西分布［16］。 采用概率解析法［2］、场景分析法［3］、复仿射方法［17］和区间分析法［18］研究风电的不确定性，这些分析法未考虑风电功率概率分布本身的不确定性，因此无法从根本上保证所提出的规划方案的有效性［19］。

本文提出一种考虑风电功率概率分布不确定性的配电网无功规划方法。该方法针对风电功率预测中只能掌握风电功率概率分布的部分信息的背景，考虑风电功率概率分布不确定性，选取出在风电功率任意一种可能的概率分布场景下均满足配电网安全运行要求，同时最小化配电网无功补偿设备投资成本和配电网有功网损之和的规划方案。采用概率分布鲁棒机会约束规划模型［20］描述含风电的配电网无功规划问题，首先根据潮流平衡等式分离节点电压和支路功率约束中的随机向量，根据条件风险价值CVaR（Conditional Value at Risk）的物理意义构建节点电压约束和支路功率约束的CVaR模型，并利用对偶优化、Schur补和S-lemma的性质，将基于CVaR的节点电压约束和支路功率约束转化为双线性矩阵不等式BMI（Bi-linear Matrix Inequality）约束，将基于 BMI约束的问题转为确定性模型，进一步提出采用基于BMI优化的免疫粒子群算法进行求解。采用改进的IEEE 33节点配电网进行仿真分析，表明了本文提出的含风电配电网无功规划策略的可行性和有效性。

1 含风电配电网无功规划模型

1.1 无功规划机会约束模型

当配电网中含有风电机组时，风电的不确定性、间歇性会给配电网的潮流带来较大的影响，将给配电网无功规划模型带来支路功率和节点电压越限的风险。在考虑风电等不确定性因素时，配电网无功规划机会约束模型通过引入机会约束规划，可避免规划方案受到小概率事件的限制，兼顾配电网系统的安全性和经济性。假设随机向量风机有功功率PW和风机无功功率QW的概率分布φ可唯一确定，通过蒙特卡罗采样，求出风电功率的确定值，得到确定的无功规划模型。通过优化计算，确定无功补偿设备的最佳位置和最佳容量，从而实现配电网有功网损和配电网无功补偿设备投资成本最小，同时满足配电网运行安全性等约束条件，具体模型如式（1）—（8）所示。

（1）目标函数。

其中，Ploss为配电网的有功网损；C1（nmQ）为关于无功补偿电容的函数，nm为各节点补偿电容的个数向量，Q为各节点无功补偿单位容量向量；C2（Ploss）为有功网损费用函数。式（1）表示无功规划旨在最小化配电网有功网损和无功电容投资费用之和。

（2）等式约束。

节点有功功率约束：

节点无功功率约束：

（3）不等式约束。

待选节点补偿电容器容量上限约束：

节点电压机会约束：

支路功率机会约束：

风电有功功率约束：

风电无功功率约束：

其中，S为节点-线路关联矩阵；PL为系统有功潮流；PLmax为系统有功潮流的上限；QL为系统无功潮流；PD、QD分别为有功和无功负荷；PW和QW分别为风机注入的有功和无功功率；Q和Qmax分别为安装的补偿电容器单位容量以及容量上限；U、Umax、Umin分别为节点电压以及节点电压的上、下限；向量PN的每个元素为相应风电机组的最大输出有功功率；向量QN的每个元素为相应风电机组的最大输出无功功率；β为设定的置信水平；φ为风电功率的概率分布，Prφ为在φ下成立的概率。

1.2 无功规划概率分布鲁棒机会约束模型

因为风电出力随时间、地形、气候等因素变化很大，风电出力包含较多的不确定信息，难以获得风电出力的概率分布函数，一般只能得到风电功率概率分布的二阶矩信息，因此不能通过蒙特卡罗采样获得准确的风电功率输出［19］。在此背景下，上述机会约束规划模型不可解。为此，本文假设已知风电功率向量PW、QW概率分布的二阶矩信息［21］，即 m 个风电机组输出有功功率和无功功率的期望值向量μ和协方差矩阵 Γ，其中 μ=［μ1，μ2，…，μm］T。 满足上述二阶矩信息的所有风电概率分布组成集合Φ（μ，Γ）。

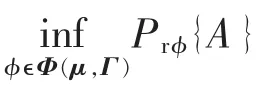
概率分布鲁棒机会约束，即式（9）和式（10）中，随机向量PW和QW的概率分布不确定，可以为期望和协方差集合Φ（μ，Γ）中的任一概率分布函数形式。由于仅知道风电功率概率分布的不确定集合，如何处理不确定集合是求解概率分布鲁棒机会约束式（9）和式（10）的难点。

2 概率分布鲁棒机会约束模型求解方法

本节首先根据潮流平衡等式分离节点电压和支路功率约束中的随机变量PW和QW，再根据CVaR的物理意义构建关于支路功率和节点电压的CVaR模型，并利用对偶优化、Schur补和S-lemma的性质，将基于CVaR的节点电压和支路功率约束转为BMI问题，并将包含随机向量的BMI问题转为确定性模型，进一步提出采用基于BMI优化的免疫粒子群算法进行求解。

2.1 分离随机变量

首先将节点电压约束式（10）化为：

根据节点电压与无功功率模型［22］，考虑无功功率是与电压幅值强耦合，与相角弱耦合，假设注入的有功功率保持不变，则ΔU=JΔq，其中，ΔU是节点电压微增量，Δq是节点注入无功功率的微增量，J是收缩的 U-q 雅可比矩阵［22］，故：

将 ΔU 代入式（11），式（11）等价于：

通过上述转化，节点电压约束转化为关于风电输出无功功率QW的函数。

令，分离式（12）中的随机变量 QW，则式（12）转化为：

根据式（2）的有功潮流平衡等式，支路功率约束可表示为关于PW的函数：

令，式（9）等价为：

2.2 基于CVaR的节点电压约束和支路功率约束模型令

风电的不确定性势必引起节点电压波动，在集合Φ（μ，Γ）中所有可能的风电概率分布函数下，约束式（13）要求节点电压约束函数L（z1）小于等于零的概率不小于置信水平 β，将 L（z1）代入式（13），则式（13）等价于：

令：

同样，风电的不确定性势必引起支路功率波动，在集合Φ（μ，Γ）中所有可能的风电概率分布函数下，约束式（15）要求支路功率约束函数L（z2）小于等于零的概率不小于置信水平 β，将 L（z2）代入式（15），式（15）等价于：

CVaR［20］是一种风险计量技术，是较VaR更优的风险计量技术，其含义为在投资组合的损失超过某个给定VaR值的条件下，该投资组合的平均损失值。VaR为一定置信水平（1-ε）下损失的阈值，而CVaR定义为：ε的CVaR为超过最大可接受损失的ε的投资组合的期望损失。

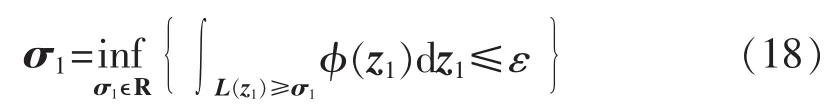
节点电压约束函数 L（z1）的条件风险定义［20］：

此处 CVaRε（L（z1））考虑了在风电概率分布函数下，CVaRε（L（z1））超出阈值的部分，因此相比阈值VaR，CVaR更保守和可靠。

对于集合Φ（μ，Γ）中任意可能的概率分布函数，已知任一风电机组出力的期望向量以及协方差矩阵，而 φ（z1）不完全已知，节点电压约束函数 L（z1）≤0成立的概率均不小于置信水平。概率分布鲁棒机会约束可使用最坏条件风险进行近似估计［20］，定义节点电压约束函数L（z1）的最坏条件风险价值WCVaR如式（20）所示［20］：

式（20）物理意义：给定节点电压阈值向量为σ1，在含风电的配电网中节点电压超出给定阈值向量σ1的概率不大于ε。

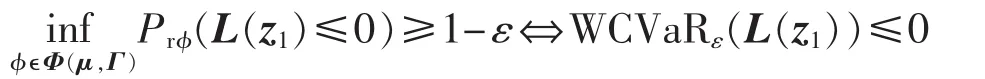
其中，Φ（μ，Γ）包含满足期望向量和协方差矩阵的所有可能的风电概率分布函数，定义如下［20］：

Φ（μ，Γ）定义式中的优化变量为非负测度φ，其约束条件分别使得φ成为一个概率测度、满足已知的一阶矩（即期望值向量）和二阶矩（即协方差矩阵）的信息。

这样，式（20）表示在所有可能的概率分布函数下，节点电压约束函数L（z1）的最坏条件风险价值超出阈值的概率低于置信水平β。

2.3 概率分布鲁棒机会约束确定性转化

以节点电压为例，本节将根据对偶优化［20］以及Schur 补［21］和 S-lemma［20］，消去节点电压最坏条件风险价值模型式（20）中的随机变量。

首先，式（20）等价于［20］：

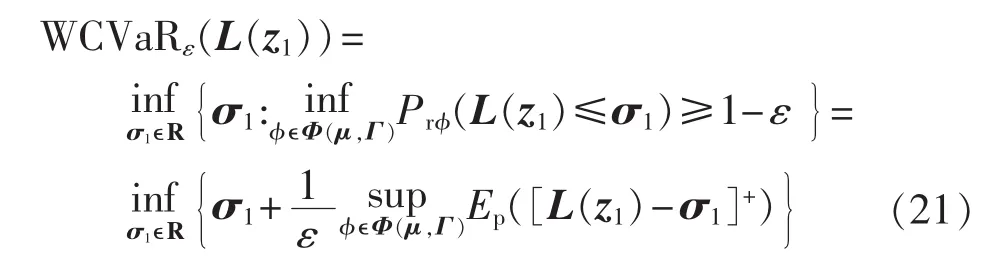
式（22）表示在所有可能的概率分布下求上确界。令 φ（z1）=［L（z1）-σ1］+，式（22）可表述为如式（23）所示的积分形式［20］：

其中，M+为Rm上的非负Borel测度锥。问题（23）的优化变量为非负测度φ，其约束条件分别使得φ成为一个概率测度、满足已知的一阶矩（即期望值向量）和二阶矩（即协方差矩阵）的信息。

由对偶理论可知式（24）与式（23）互为对偶问题，并且满足强对偶定理：ZP=ZD。

其中，y0、y、Y 分别为对应于问题（23）中第一、二、三条约束的对偶变量；Tr（·）表示迹运算。因此θwc对应于对偶问题式（24）的最优值。定义如下变量，其中Mk1为包含对偶变量的对称矩阵：

根据Shur补，式（24）写成矩阵的形式：

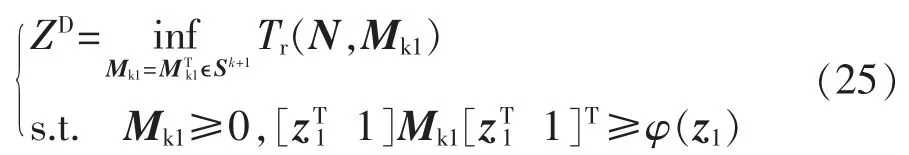
由 S-lemma，将上式中约束写成双线性矩阵不等式形式［20］，等价于：

其中，αi为比例参数。此时式（25）等价于：

式（27）所计算的仅仅是最坏条件期望部分，将其代入式（21），那么，式（21）等价于：

当最坏条件风险价值不大于0时，式（16）所示的概率分布鲁棒机会约束成立［20］。 因此，式（10）所示的节点电压约束子问题的可行解为：

同理，式（9）支路功率约束子问题的可行解为：

经过上述转化，式（29）和式（30）中不包含随机变量QW，将式（29）和式（30）代入概率分布鲁棒机会约束模型（式（1）—（4）、式（7）—（10））中，该概率优化问题转化为确定性模型：

注意到式（31）所示的确定性模型中不包含随机变量，仅包含随机变量的二阶矩信息。

3 基于双线性矩阵不等式优化的粒子群算法

式（31）的确定性模型中，仅需要随机变量风电功率的二阶矩信息。本节给出含不同二阶矩风电的配电网最优无功规划方案的求解算法。采用粒子群算法求解问题式（31），具体计算流程如图1所示。首先给定配电网原始参数、风电功率的二阶矩（即风电机组接入节点有功和无功出力的期望值和协方差以及取值范围）以及粒子群算法参数。将节点电压约束和支路功率约束的概率分布鲁棒机会约束模型式（10）和式（9）转化为式（29）、式（30）所示的 BMI形式，利用矩阵正定的判定条件求出约束条件对应的可行解，在此基础上进行潮流计算，计算种群的个体在各场景下的网损和无功补偿设备投资成本和，再评估种群中个体的适应度。通过选择疫苗、接种疫苗和免疫选择的优化计算流程，得到全局最优解。

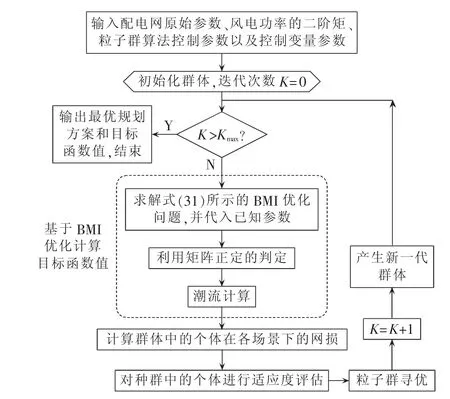
图1 基于BMI优化的粒子群算法流程图Fig.1 Flowchart of PSO algorithm based on BMI optimization

4 算例仿真与分析

采用改进的IEEE 33节点配电网进行仿真计算。IEEE 33节点配电网如图2所示，系统电压等级为12.66 kV，总有功负荷为3715 kW，总无功负荷为2300 kvar。节点16、23、26处接入风机。节点电压的上、下限分别是1.05 p.u.和0.95 p.u.。有功网损电能单价为0.33元／（kW·h）。每组电容器固定投资费为5000元，使用年限为3 a，待选节点补偿电容器容量上限为0.54Mvar。本文以电容器的使用年限作为一个规划周期。

图2 改进的IEEE 33节点配电网接线图Fig.2 Diagram of modified IEEE 33-bus distribution network

为分析本文方法特点，比较了传统机会约束规划方法和本文概率分布鲁棒机会约束规划方法下，满足支路功率和节点电压安全约束下的无功规划方案。为分析风电功率不确定性对无功规划方案的影响，测试了采用本文方法后不同风电功率概率分布均值和协方差下的无功规划方案总费用。本文考虑了m

其中μm为第m个风电场风电功率概率分布出力的期望值，σij（i，j=1，2，…，m）为风电场 i、j之间的风电功率概率分布协方差，仿真时取每个风电场的风电功率概率分布期望值及每个协方差均相等。

4.1 概率分布鲁棒机会约束方案与传统机会约束规划方案比较

风电均值为500 kW，协方差为100 kW2，当设定不同的置信水平时，无功规划方案总费用如图3所示。当风电功率均值为400 kW，协方差为100 kW2时，概率分布鲁棒机会约束最优规划方案与传统机会约束最优规划方案如表1所示。

图3 概率分布鲁棒优化无功规划和传统机会约束无功规划最优方案总费用Fig．3 Total cost for reactive power planning schemes optimized by distributional robust chance constraint and traditional chance constraint

表1 概率分布鲁棒机会约束与传统机会约束最优方案比较Table1 Comparison of optimal planning scheme between distributional robust chance constraint and traditional chance constraint

由表1和图3可知，随着系统设置的支路功率和节点电压约束的置信水平的提高，2种方法得到的无功补偿电容数量逐渐增多，总费用也逐步增多。其主要原因是在考虑风电的不确定性的情况下，随着系统的置信水平的提高，为避免因风电随机性造成安全约束越界，需要增加无功补偿电容，造成配电网网损和无功补偿设备投资成本之和增大。

当置信水平在0.5～0.95时，概率分布鲁棒机会约束法比传统机会约束法需要的无功补偿电容的数量多，相应地，系统的总费用也较多。其主要原因是概率分布鲁棒优化法要求对于任意可能的风电概率分布情况，系统均要满足给定置信水平下设定的支路功率和节点电压约束，从而对配电网无功规划要求更高。

当置信水平取0.95时，表示对于绝大多数可能的风电功率概率分布的取值场景下，各支路功率和节点电压均满足系统安全运行要求，此时，风电功率概率分布的具体形式对无功规划最优方案的影响非常小，概率分布鲁棒机会约束法与传统机会约束法的最优方案总费用非常接近。

4.2 当协方差为100 kW 2时不同均值下总费用

协方差相同，当设定不同的支路功率和节点电压的置信水平β时，不同均值下总费用如图4所示。

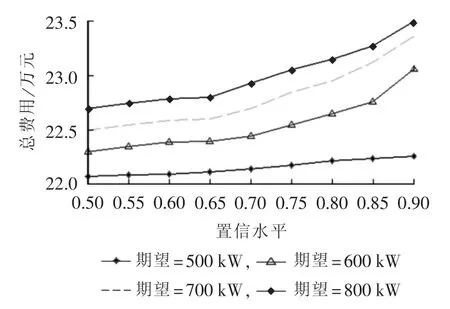
图4 协方差为100 kW 2时不同风电功率均值下的总费用Fig．4 Total cost for different values of wind-power mean when covariance is 100 kW 2

由图4可见，当风电功率概率分布均值和二阶矩固定，随着置信水平的提高，总费用变多。这是因为当配电网安全约束的置信水平提高，为避免因风电随机性造成安全约束越界，需要增加无功补偿电容，造成总费用增多。同时，当风电功率概率分布协方差和置信水平相同，不同风电功率概率分布均值下，均值越大，配电网网损和无功补偿电容投资成本之和越大。这是因为均值越大，风电注入系统功率增加，导致系统网损和无功补偿电容投资成本之和增加，从而无功规划方案总费用增加。

4.3 当均值为500 kW时不同协方差下总费用

风电功率概率分布均值相同，当设定不同的支路功率和节点电压的置信水平β时，不同风电功率概率分布协方差下总费用如图5所示。由图5可知，当风电功率的均值和置信水平相同时，风电功率概率分布协方差越大，配电网网损和无功补偿电容投资成本之和越大。这是因为协方差越大，风电功率的波动范围增大，对系统中线路潮流的影响变大，无功补偿电容数量增多，从而无功规划方案总费用增加。

图5 均值为500 kW时不同风电功率协方差下的总费用Fig．5 Total cost for different values of windpower covariance when mean is 500 kW

5 结论

针对无法获得准确的风电功率概率分布函数的情况，本文提出一种考虑风电功率概率分布不确定性的含风电配电网无功规划方法。采用概率分布鲁棒机会约束规划模型描述含风电的配电网无功规划问题，选取在任意一种概率分布函数下，系统支路功率和节点电压均满足安全运行约束的无功规划方案。算例分析表明，概率分布鲁棒机会约束规划方法可以在风电概率分布函数部分信息的情况下，制定满足一定置信水平的配电网无功规划方案。

在含风电的配电网规划模型中，采用视在功率对支路功率约束进行建模更符合实际工程情况，将是下一步的研究工作。

［1］胡海燕，武晓朦，刘健.基于遗传算法的配电网低压侧无功补偿动态优化规划［J］. 电力自动化设备，2005，25（3）：25-29.HU Haiyan，WU Xiaomeng，LIU Jian.Genetic algorithm based optimal dynamic planning of low-voltage side reactive power compensators［J］.Electric Power Automation Equipment，2005，25（3）：25-29.

［2］张沈习，程浩忠，张立波，等.含风电机组的配电网多目标无功规划［J］. 电力系统保护与控制，2013，41（1）：40-46.ZHANG Shenxi，CHENG Haozhong，ZHANG Libo，et al.Multiobjective reactive power planning in distribution system incorporating with turbine generation［J］.Power System Protection and Control，2013，41（1）：40-46.

［3］KARAMI M，SHAYANFAR H A，AGHAEI J，et al.Scenariobased security-constrained hydrothermal coordination with volatile wind power generation［J］.Renewable and Sustainable Energy Reviews，2013，28：726-737.

［4］袁越，吴博文，李振杰，等.基于多场景概率的含大型风电场的输电网柔性规划［J］. 电力自动化设备，2009，29（10）：8-12.YUAN Yue，WU Bowen，LI Zhenjie，et al.Flexible planning of transmission system with large wind farm based on multiscenario probability［J］.Electric Power Automation Equipment，2009，29（10）：8-12.

［5］郑智，周双喜，徐飞，等.基于多场景和模糊技术的综合无功规划［J］. 电力系统自动化，2007，31（4）：41-45.ZHENG Zhi，ZHOU Shuangxi，XU Fei，et al.Comprehensive reactive power planning based on multi-scenario and fuzzy technique［J］.Automation of Electric Power Systems，2007，31（4）：41-45.

［6］ATWA Y M，EL-SAADANY E F，SALAMA M M A，et al.Optimal renewable resources mix for distribution system energy loss minimization［J］.IEEE Trans on Power Systems，2010，25（1）：360-370.

［7］温步瀛，江岳文，陈冲.风电场并网运行的无功补偿优化问题［J］. 电力自动化设备，2008，28（5）：42-46.WEN Buying，JIANG Yuewen，CHEN Chong.Reactive power compensation optimization for grid-connected wind farm［J］.Electric Power Automation Equipment，2008，28（5）：42-46.

［8］周冬旭，李晓明.面向电力市场的含风电机组配电网无功优化模型及其求解算法［J］. 电力自动化设备，2013，33（4）：24-29.ZHOU Dongxu，LI Xiaoming.Reactive power optimization model and its algorithms for distribution system with wind farm in electricity market［J］.Electric Power Automation Equipment，2013，33（4）：24-29.

［9］江洁，王主丁，张宗益，等.基于有效生成初始种群的配电网无功规划优化遗传算法［J］. 电网技术，2009，33（8）：60-65.JIANG Jie，WANG Zhuding，ZHANG Zongyi，et al.Effective initial population generation based genetic algorithm for optimal capacitor placement in radial distribution networks［J］.Power System Technology，2009，33（8）：60-65.

［10］张粒子，舒隽，林宪枢，等.基于遗传算法的无功规划优化［J］.中国电机工程学报，2000，20（6）：6-9.ZHANG Lizi，SHU Jun，LIN Xianshu，et al.Reactive power planning based on genetic algorithm［J］.Proceedings of the CSEE，2000，20（6）：6-9.

［11］史宇伟，潘学萍.计及历史气象数据的短期风速预测［J］.电力自动化设备，2014，34（10）：75-80.SHI Yuwei，PAN Xueping.Short-term wind speed forecasting considering historicalmeteorological data［J］.Electric Power Automation Equipment，2014，34（10）：75-80.

［12］雷若冰，徐箭，孙辉，等.基于相关性分析的风电场群风速分布预测方法［J］. 电力自动化设备，2016，36（5）：134-139.LEI Ruobing，XU Jian，SUN Hui，et al.Wind speed distribution forecasting based on correlation analysis for wind farm group［J］.Electric Power Automation Equipment，2016，36（5）：134-139.

［13］ZHANG H，LI P.Chance constrained programming for optimal power flow under uncertainty［J］.IEEE Trans on Power Systems，2011，26（4）：2417-2424.

［14］ZOU Kai，AGALGAONKAR A P，MUTTAQI K M，et al.Distribution system planning with incorporating DG reactive capability and system uncertainties［J］.IEEE Trans on Sustainable Energy，2012，3（1）：112-123.

［15］TEWARI S，GEYER C J，MOHAN N.A statistical model for wind power forecast error and its application to the estimation of penalties in liberalized markets［J］.IEEE Trans on Power Systems，2011，26（4）：2031-2039.

［16］DELFANTI M，GRANELLI G P，MARANNINO P，et al.Optimal capacitor placement using deterministic and genetic algorithms［J］.IEEE Trans on Power Systems，2000，15（3）：1041-1046.

［17］王守相，韩亮.DG出力不确定性对配电网影响力分析的复仿射数学方法［J］. 中国电机工程学报，2014，34（31）：5507-5515.WANG Shouxiang，HAN Liang.Complex affine arithmetic based method for the analyses of DG’s uncertainty influence on distribution network［J］.Proceedings of the CSEE，2014，34（31）：5507-5515.

［18］王守相，王栋，韩亮.考虑不确定性的微网日前经济优化调度区间线性规划方法［J］. 电力系统自动化，2014，38（24）：5-12.WANG Shouxiang，WANG Dong，HAN Liang.Interval linear programming method for day-ahead optimal economic dispatching of microgrid considering uncertainy［J］.Automation of Electric Power Systems，2014，38（24）：5-12.

［19］BIAN Qiaoyan，XIN Huanhai，WANG Zhen，et al.Distributionally robust solution to the reserve scheduling problem with partial information of wind power［J］.IEEE Trans on Power Systems，2015，30（5）：2822-2823.

［20］ZYMLER S，KUHN D，RUSTEM B.Distributionally robust joint chance constraints with second-order moment information ［J］.Mathematical Programming，2013，137（1）：167-198.

［21］YANG W，XU H.Distributionally robust chance constraints for non-linear uncertainties［J］.Mathematical Programming，2016，155（1）：231-265.

［22］王锡凡，方万良，杜正春.现代电力系统分析［M］.北京：科学出版社，2003：431-438.