基于LOF和SVM的智能配电网故障辨识方法

胡 伟 ，李 勇，曹一家 ，张志鹏，赵庆周 ，段义隆

（1.湖南大学 电气与信息工程学院，湖南 长沙 410082；2.山东电力工程咨询院有限公司，山东 济南 250013）

0 引言

随着智能配电网容量的不断增加以及分布式电源（DG）的接入，配电网的网络结构和运行方式日益复杂，使得传统的继电保护方法难以满足要求［1-6］。在配电网发生故障后快速有效地诊断出故障位置、辨识故障类型，这对减少故障恢复时间、提高配电网的安全稳定运行和供电的可靠性具有重要意义。

对于配电网故障定位而言，通常是利用故障点前后三相电流突变量的大小和波形的不一致，来识别故障区域［7］；通过比较有源配电网故障和非故障区段两侧的短路电流幅值的关系，实现故障定位［8］；通过限制分布式电源接入配电网的容量，基于短路电流计算，设置合理的开关整定值，用以区分系统电源提供的最小短路电流和分布式电源提供的最大短路电流，再采用传统的继电保护方法进行故障区域定位［9］。以上保护方法都能较好地实现故障定位，但所取故障特征量比较单一，当发生传感器失效或者通信异常时，容易引起保护装置的拒动或误动，且存在复杂的整定值计算。本文提出的局部异常因子（LOF）无整定保护算法充分利用广域测量系统上传的实时数据，以零序、负序、正序三相电流以及零序有功、无功功率等多个电气特征量进行故障定位。

当配电网发生永久性故障时，应迅速判断出故障区域，并对故障区域的故障类型进行人工检修，待查明故障原因后才能恢复正常供电，这在一定程度上增加了故障排除时间和人员的调配，且对于一些关键负荷的持续供电有一定的影响。因此，如何迅速地界定故障区域并判定故障类型具有一定的实际意义。

考虑到小电流接地系统发生单相接地故障时，其故障信号难以检测，且故障电压、电流信号受系统运行方式和故障位置等影响［10］，因此，如何利用保护装置采集到的电压、电流信号提取故障特量，这对配电网故障类型辨识至关重要。由于小波变换、经验模式分解对处理非线性、非平稳信号具有很大优越性，文献［11-13］提出基于对暂态电压、电流的分解，从各分量中提取反映故障信号的故障特征量，利用信息熵或近似熵指标，对故障特征量进行量化统计。随着人工智能的不断发展，神经网络算法在智能电网暂态保护、故障选线等方面有着广泛的应用，但该算法容易陷入局部最小值，且所需样本很大、收敛速度很慢［14］。因此，神经网络算法在智能电网故障处理方面存在不足，而支持向量机（SVM）算法能很好地解决以上问题。SVM算法所需样本少且相对于神经网络有更好的收敛速度和泛化能力。电力系统故障发生的概率很小，要求对故障做出迅速的处理，属于小样本事件，因此采用SVM分类器具有很大优势［15］。

鉴于此，本文提出一种基于LOF和SVM的故障定位与故障类型辨识方法。该方法的基本思想是利用广域测量系统上传信息，通过数据预处理与数据融合形成多维状态监测矩阵，对该矩阵进行多维尺度分析并计算其LOF值，根据各节点的LOF值大小对配电网网络进行故障定位；然后对故障区域暂态三相电压进行小波变换，结合奇异值分解和信息熵理论，以三相电压的小波奇异熵值作为SVM的输入量，通过仿真模拟不同故障区域的各种故障类型，对其样本进行训练，从而准确地判断故障相，并以反映接地故障信号的零序电压低频能量判别是否为接地故障。通过MATLAB仿真，验证了本文算法的可行性，该算法能比较精准地实现智能配电网故障定位和故障类型判别，且不受过渡电阻、故障位置等影响。

1 智能配电网故障定位算法

广域测量系统根据测量保护装置上传的数据，对当前智能配电网的运行状态进行实时监测。根据上传的带有统一时标的电流与功率信息，通过数据预处理与数据融合，形成包含多个电气特征量的多维状态监测矩阵，并对此矩阵进行多维尺度降维和LOF检测。如存在离群点，则判定有故障发生，再根据各节点LOF值的大小迅速地界定故障区域。

1.1 数据预处理与数据融合

由于广域测量系统数据量大且故障信息不明显，为了减少数据量、提高运行效率，要对原始数据进行预处理。数据预处理包括故障特征量选取、网络关联矩阵构建以及区域差分处理。故障特征量的选取是为了确保智能配电网状态监测的准确性和时效性。本文故障定位环节选取电流和功率2种类型的电气特征量，能可靠识别不同类型的故障。网络关联矩阵是明确网络各节点之间、各节点与各区域之间的相对关系，为区域差分处理提供依据。区域差分的目的是对状态监测数据进行规范化处理，进一步增加故障节点和正常节点的差异性，提高辨识准确性。

数据融合的目的是构建包含多个电气特征量的高维状态监测矩阵。首先，在空间上将多个不同的单电气特征量状态监测矩阵融合成多电气特征量状态监测矩阵；然后，将该矩阵在时间序列上进行扩充，形成多时段多电气特征量的高维时空状态监测矩阵。

1.2 多维尺度分析

多维尺度分析是对高维状态监测矩阵进行降维处理，是根据各节点的相对距离来表征各节点的相似程度。当配电网正常运行时，构建的高维时空状态监测矩阵的行间差异度较小，不存在离群点。当配电网故障时，故障节点和非故障节点差异度很大，会有少量节点偏离正常节点形成离群点。对高维时空状态监测矩阵进行多维尺度降维的过程如下。

a.计算高维时空状态监测矩阵各对象间的欧氏距离，形成各节点的相似度矩阵 D=（dij），dij由式（1）得到。

其中，xik、xjk分别为高维时空状态监测矩阵的第i行与第j行的第k个元素。

b.根据相似度矩阵，计算中心内化积矩阵。

c.求解中心内化积矩阵的前2个特征根λ1、λ2及对应的正交化特征向量，并使得：

其中，分别为第 i个特征根对应的正交化特征向量及其转置。

d. 令 X= （x（1），x（2）），X 为高维时空状态监测矩阵在二维空间的表示。

1.3 LOF检测算法

LOF检测算法对离群点有较高的灵敏性。当配电网正常运行时，不存在离群点，各节点的LOF值近似为1；当配电网故障时，离群点的LOF值很大，正常节点的LOF值仍然维持在1左右。因此，可根据LOF值的大小，来进行故障定位。采用高维时空状态监测矩阵降维后得到的矩阵X进行LOF检测的步骤如下。

a.求取各节点与距其最近的节点的距离，即K距离 Kdist（p）。

b.计算各节点的K邻域Nk（p）：

其中，dist（p，q）为数据中第p个对象与第 q个对象之间的空间距离。

c. 确定各节点的局部可达距离 Dreach（p，q）：

d.计算各节点的局部可达密度ρIrdk（p）：

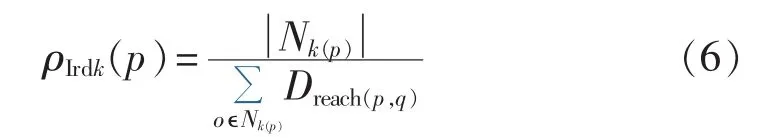
其中，o 为 K 邻域 Nk（p）中的任意对象。

e.求解各对象的局部异常因子fLOFk（p）：

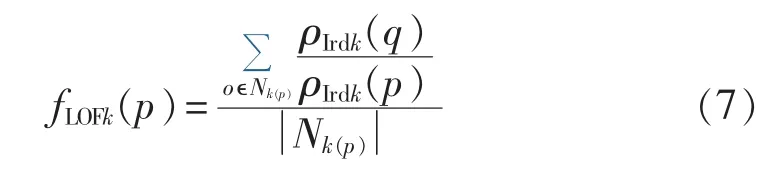
2 智能配电网故障类型判别

2.1 故障特征量的提取

当配电网发生单相接地故障时，其三相电压瞬态值呈现出非线性、非平稳的信号，因此利用小波变换的时频多分辨率的特点，提取反映接地故障信息的零序电压低频信号能量作为电气特征量，用于判定是否发生接地故障。但对三相电压进行小波变换后，仅依靠小波时频特性不足以识别不同故障下的故障相，还需考虑对小波变换后的小波系数矩阵再进行奇异值分解，最后把分解后的对角矩阵处理成一个概率分布序列并计算其小波奇异熵值，用该序列的小波奇异熵值来反映三相电压信号的故障相。

对信号U（n）进行m层分解之后的小波系数低频分量和小波系数高频分量分别为Am（n）和Bm（n）。对应在单一尺度下的小波低频和高频能量分别为EL=‖Am（n）‖2和 EH=‖Bm（n）‖2（m=1，2，…，M，其中M为小波分解层数）。本文选取零序电压第一层低频能量来判定是否有接地故障。信号U（n）的m个分量可构成一个m×n的小波系数矩阵W，对其进行奇异值分解［16-17］，则矩阵W可表示为：

其中，U和V分别为m×m和n×n阶正交矩阵；S为广义对角矩阵，其对角元素按降序排列。

三相电压信号的小波系数矩阵W经奇异值分解后，其对角矩阵能很好地反映故障信号的时频分布特征。由于接近于零的元素难以反映故障信号的特征，为了减少计算量，可以忽略。

信息熵是衡量信息量的一种尺度，也是对系统信息的一种量化。如果系统有序，则系统熵值较低；如果系统混乱，则系统熵值高。因此，利用信息熵理论，能很好地对系统的有序度进行量化统计。对三相电压进行奇异值分解后，若对角元素越平均，则系统故障特征越明显，系统熵值越大；反之，则信号故障量少，或者不包含故障信号，系统熵值就越小。小波奇异熵值是基于小波变换、奇异值分解以及信息熵相结合的产物［18-19］。将三相电压经小波变换后的系数矩阵进行奇异值分解，奇异值能反映原三相电压信号的基本特征；再利用信息熵的统计特性把分解之后的对角矩阵处理成一个概率分布序列并计算其小波奇异熵值，用该小波奇异熵值作为故障特征量来反映系统故障相。

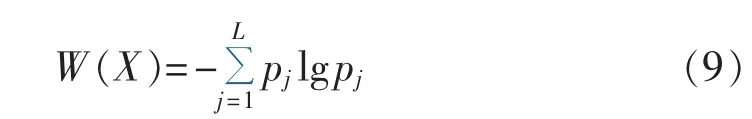
结合小波分析和奇异值分解理论，小波奇异熵值计算式如下：

其中，K和L为对角元素个数。本文选取前9个有效对角元素。

本文仿真分析部分提到的含双分布式电源的10 kV配电网系统，其中区域Z4在不同故障下三相电压小波奇异熵值和反映接地故障信息的零序电压第一层低频信号能量值如表1所示。

表1 区域四故障时的故障特征量Table1 Characteristic parameters for different fault types of Section 4

根据信息熵理论，如果信号不稳定，则小波奇异熵值会越大，故障相的小波奇异熵值大于非故障相。因此，选择合适的阈值，可作为判定故障相的依据。经过大量实验，本文选取阈值θ=0.5，小波奇异熵值大于0.5为故障相，小于0.5为非故障相。利用反映接地故障信息的零序电压第一层低频信号能量预判是否有接地故障。

2.2 基于SVM的故障类型判定

支持向量机是一种新的模式识别方法，能够较好地解决非线性问题，特别适用于小样本分析。其基本原理是通过寻找最优分类面，使对线性可分的样本分类间隙最大。对于线性不可分问题，通常引入核函数，把低维非线性不可分样本映射到某个高维线性可分空间，在变换后的高维空间寻求最优分类面，核函数的引入实现了非线性变换后的线性分类，但计算复杂度没有增加。

如图1所示，SVM在处理小样本二分类问题时具有优势，能将低维线性不可分的问题转换到高维空间线性可分。由于电力系统故障不是经常发生，属于小概率事件，且基本故障类型较少，所需要样本数目也不多，因此相应的SVM分类器数目也较少，这在一定程度上提高了SVM训练速度和决策速度。

图1 线性和非线性样本空间SVM分类Fig.1 SVM classification of linear or nonlinear sample space

以三相电压信号的小波奇异熵值为故障特征量，通过大量仿真，获取一定数目的样本，组成特征样本空间，建立基于SVM分类器的故障识别模型，以快速辨识故障区域的故障相。本文所提算法整体流程如图2所示，通过对状态监测矩阵进行多维尺度分析和离群点检测能实现对配电网的实时监控，一旦检测故障发生，能迅速界定故障区域，并提取故障特征量，以故障处的零序电压第一层低频能量对故障类型进行初步分类，将故障分为接地故障和相间短路故障，再通过SVM故障识别模型具体判定为哪一类故障。SVM能正确识别不同故障区域的不同故障类型。

图2 故障定位与故障类型判别流程Fig.2 Flowchart of fault location and fault type identification

3 仿真分析

3.1 系统参数以及故障识别

本文以含双分布式电源的某智能配电网示范区为研究对象，验证算法的可行性。该配电网的拓扑结构如图3所示。系统电压等级为10 kV，仿真采样频率为20 kHz，仿真时间为0.5 s，故障发生时刻在0.2 s，测控终端之间线路长度为6～8 km。考虑不同线路不同类型故障，通过大量仿真建立故障样本库。当故障发生时，用多维尺度分析和LOF算法定位故障区域，提取故障区域故障特征量，以三相电压小波奇异熵值作为SVM输入量以判别故障相，以零序电压第一层低频能量来判定是否发生接地故障。

图3 某10 kV含分布式电源的配电网拓扑图Fig.3 Topology of a 10 kV distribution network with DGs

3.2 单相接地故障

以馈线区域Z4发生A相接地故障为例，状态监测矩阵数据如图4所示。由图4可见，节点4、5以及广义节点17远离其他节点，LOF值在90左右，而在多维尺度降维结果图中出现离群点，故可判定区域Z4为故障区域。

图4 区域Z4故障时状态监测矩阵数据分析结果Fig.4 Results of data analysis for status monitoring matrix when fault occurs in Section Z4

SVM故障类型判别结果如图5所示。图5（a）的纵轴刻度中，1、2、3对应单相接地故障，分别为AG、BG、CG 故障；4、5、6 对应相间接地短路故障，分别为ABG、BCG、ACG故障；对不同故障各取10组样本进行训练，横坐标1—60为对应训练样本点，样本点61为待测样本，经过SVM训练判定样本点61归为第一类，属于AG故障。由图5（b）可以看出，故障分类相对误差在0.1%以内。

图5 区域Z4故障处的故障类型判别结果Fig.5 Results of fault type identification when fault occurs in section Z4

3.3 两相短路故障

当区域母线节点Z5发生AB两相短路故障时，状态监测矩形数据分析结果见图6。由图6可看出，节点5、6、9以及广义节点17远离其他节点，且LOF值在270左右，而在多维尺度降维结果图中出现离群点，故可判定区域Z5为故障区域。

图6 区域Z5故障时状态监测矩阵数据分析结果Fig.6 Results of data analysis for status monitoring matrix when fault occurs in section Z5

SVM故障类型判别结果如图7所示。图7（a）的纵轴刻度中，1、2、3对应两相短路故障，分别为AB、BC、AC短路故障；4对应三相短路故障，为ABC短路；对不同故障各取10组样本进行训练，横坐标1—40为对应训练样本点，样本点41为待测样本，经过SVM训练判定样本点41归为第一类，属于AB短路故障。故障分类相对误差在0.1%以内。

图7 区域Z5故障处的故障类型判别Fig.7 Results of fault type identification when fault occurs in section Z5

4 结论

本文提出了一种LOF和SVM算法相结合的故障定位与故障类型判别方法。首先对配电网海量数据进行数据预处理与数据融合，选择电流和功率2个电气特征量，利用LOF检测方法对故障进行定位；再对故障处的三相电压进行小波变换，把变换后的小波系数矩阵进行奇异值分解，利用信息熵理论，把分解之后的对角矩阵处理成一个概率分布序列并计算其小波奇异熵值，用该小波奇异熵值来辨识三相电压信号的故障相，并用零序电压第一层低频能量对故障类型进行初步分类；最后以三相电压的小波奇异熵值为样本空间建立SVM故障分类模型，用于判定故障类型。通过仿真分析验证了本文方法的有效性。

研究表明，根据各节点的LOF值进行故障定位，不需比较电气特征量，避免了复杂的整定计算；小波奇异熵值能简洁地区分不同复杂度的信号，因此能识别不同故障下的故障相；根据三相电压的小波奇异熵值能准确判别故障类型。

［1］傅旭．含分布式电源的配电网故障分析的解耦相分量法［J］．电力自动化设备，2009，29（6）：19-23．FU Xu．Decoupling phase domain method for fault analysis of distribution system with distributed generation［J］．Electric Power Automation Equipment，2009，29（6）：19-23．

［2］马静，王希，米超，等．含分布式电源的配电网自适应保护新方法［J］．电网技术，2011，35（10）：204-208．MA Jing，WANG Xi，MI Chao，et al．A new adaptive protection approach for distribution network containing distributed generation［J］．Power System Technology，2011，35（10）：204-208．

［3］SALIM R H，SALIM K C O，BRETAS A S．Further improvements on impedance-based fault location for power distribution systems［J］．IET Generation，Transmission & Distribution，2011，5（4）：467-478．

［4］余琼，余胜，李晓晖．含分布式电源的配电网自适应保护方案［J］．电力系统保护与控制，2012，40（5）：110-115．YU Qiong，YU Sheng，LI Xiaohui．An adaptive protection scheme for meshed distribution system with DG ［J］．Power System Protection and Control，2012，40（5）：110-115．

［5］SHAMAM F A，RAMACHANDARAMURTUY V K，MITHULANANTHAN N．Fault-location scheme for power distribution system with distributed generation ［J］．IEEE Transactions on Power Delivery，2015，30（3）：1187-1195．

［6］刘健，张小庆，同向前，等．含分布式电源配电网的故障定位［J］．电力系统自动化，2013，37（2）：36-42．LIU Jian，ZHANG Xiaoqing，TONG Xiangqian，et al．Fault location for distribution systems with distributed generations［J］．Automation of Electric Power Systems，2013，37（2）：36-42．

［7］宋国兵，李广，于叶云，等．基于相电流突变量的配电网单相接地故障区段定位［J］．电力系统自动化，2011，35（21）：84-90．SONG Guobing，LI Guang，YU Yeyun，et al．Single-phase earth fault section location based on phase currrent fault component in distribution network［J］．Automation of Electric Power Systems，2011，35（21）：84-90．

［8］高孟友，徐丙垠，张新慧．基于故障电流幅值比较的有源配电网故障定位算法［J］．电力自动化设备，2015，35（7）：21-25．GAO Mengyou，XU Bingyin，ZHANG Xinhui．Fault location based on fault current amplitude comparison for active distribution network［J］．Electric Power Automation Equipment，2015，35（7）：21-25．

［9］郑涛，贾仕龙，潘玉美，等．基于配电网原故障定位方案的分布式电源准入容量研究［J］．电网技术，2014，38（8）：2257-2262．ZHENG Tao，JIA Shilong，PAN Yumei，et al．Research on allowed penetration level of DGs based on the traditional fault location methods［J］．Power System Technology，2014，38（8）：2257-2262．

［10］薛永端，徐丙垠，李天友，等．配电自动化系统小电流接地故障暂态定位技术［J］．电力自动化设备，2013，33（12）：27-33．XUE Yongduan，XU Bingyin，LI Tianyou，et al．Small-current grounding fault location based on transient signals of distribution automation system［J］．Electric Power Automation Equipment，2013，33（12）：27-33．

［11］何正友，陈小秦，罗国敏，等．基于暂态电流小波熵权的输电线路故障选相方法［J］．电力系统自动化，2006，30（21）：39-43．HE Zhengyou，CHEN Xiaoqin，LUO Guomin，et al．Faulted phase selecting method of transmission lines based on wavelet entropy weight of transient current［J］．Automation of Electric Power Systems，2006，30（21）：39-43．

［12］杨健维，罗国敏，何正友．基于小波熵权和支持向量机的高压输电线路故障分类方法［J］．电网技术，2007，31（23）：22-26．YANG Jianwei，LUO Guomin，HE Zhengyou．High voltage transmission line fault classification based on entropy weight of wavelet and support vector machines［J］．Power System Technology，2007，31（23）：22-26．

［13］何正友，符玲，麦瑞坤，等．小波奇异熵及其在高压输电线路故障选相中的应用［J］．中国电机工程学报，2007，27（1）：31-36．HE Zhengyou，FU Ling，MAI Ruikun，et al．Study on wavelet singular entropy and its application to faulty phase selection in HV transmission lines［J］．Proceedings of the CSEE，2007，27（1）：31-36．

［14］唐金锐，尹项根，张哲，等．配电网故障自动定位技术研究综述［J］．电力自动化设备，2013，33（5）：7-13．TANG Jinrui，YIN Xianggen，ZHANG Zhe，et al．Survey of fault location technology for distribution networks［J］．Electric Power Automation Equipment，2013，33（5）：7-13．

［15］何旭，姜宪国，张沛超，等．基于SVM的小样本条件下继电保护可靠性参数估计［J］．电网技术，2015，39（5）：1432-1437．HE Xu，JIANG Xianguo，ZHANG Peichao，et al．SVM based parameter estimation of relay protection reliability with small samples［J］．Power System Technology，2015，39（5）：1432-1437．

［16］HOU Zujun．Adaptive singular value decomposition in wavelet domain for image deposing［J］．Pattern Recognition，2003，36（8）：1747-1763．

［17］梁霖，徐光华，刘弹，等．小波-奇异值分解在异步电机转子故障特征提取中的应用［J］．中国电机工程学报，2005，25（19）：111-115．LIANG Lin，XU Guanghua，LIU Dan，et al．A feature extraction method of rotor faults of induction motor based on continuous wavelet transform and singular value decomposition［J］．Proceedings of the CSEE，2005，25（19）：111-115．

［18］ROSSON O A，BLANCO S，YORDANOVA J，et al．Wavelet entropy：a new tool for analysis of short duration brain electrical signals［J］．J Neurosci Meth，2001，105（1）：65-75．

［19］BLANCO S，FIGLIOSA A，QUIAN Q R，et al．Time-frequency analysis of electroencephalogram series（Ⅲ）：information transfer function and wavelets packets［J］．Physical Review E，1998，57（1）：932-940．