基于用户出行需求的电动汽车充电站规划
陈静鹏,艾 芊,肖 斐
(上海交通大学 电气工程系 电力传输与功率变换控制教育部重点实验室,上海 200240)
0 引言
日益突出的能源紧缺与环境污染问题为电动汽车EV(Electric Vehicle)的发展带来了前所未有的机遇。2015年,我国的EV销量呈现爆发式增长,然而,目前EV的续航里程和传统燃油汽车相比还不具备优势,需要分布广泛的充电设施提供电量保障。为此,国家发改委出台了《电动汽车充电基础设施发展指南(2015—2020年)》。 文件提出,到2020年,新增集中式充换电站超过1.2万座,分散式充电桩超过480万个,以满足全国500万辆EV的充电需求。充换电站的合理规划,是实现EV有序充电控制[1-4]的前提,不仅能够提高充换电站自身的经济效益和运营管理水平,还能为EV提供舒适便捷的充电服务,是推广EV应用的基础,具有重要的实际意义。
目前,国内外学者已经对充电站的优化布局进行了开拓性的研究,主要集中在城区公路充电站和城际高速公路充电站2个方面。文献[5]以服务的EV数量最大化为目标确定充电站选址,以充电站的服务成本和顾客的等待费用之和最小化为目标配置充电站规模,实现高速公路充电站的优化规划;文献[6]在估计高速公路EV充电需求的基础上,采用连续的选址模型对充电站进行优化配置,以克服EV充电需求的不确定性给充电设施规划带来的挑战;文献[7]在分析EV换电需求空间分布的基础上,结合Voronoi图划分换电站服务区域,服务区域内EV的换电需求决定换电站的规模,以此实现换电站的最优规划;文献[8]提出一种以功率平衡、电池管理、安装容量为约束,以运行成本最低为目标的换电站和分布式电源的最优规划模型,有效地提高了配电网运行的经济性和安全性;文献[9]以俘获的交通流量最大、配电系统网络损耗最小以及节点电压偏移最小为目标,建立了充电站最优规划的多目标决策模型,并采用改进的二进制粒子群优化算法进行求解。
可见,分析EV充电需求的时空分布是进行充电站规划的基础。然而,上述文献均认为充电需求的空间分布是静态不变的,忽略了规划方案对EV充电需求的影响。事实上,EV趋向于选择便捷的充电站进行充电,充电站的布局反过来也会影响EV充电需求的空间分布,两者之间存在相互耦合的关系。另一方面,上述文献对充电站进行选址时没有考虑EV用户的出行需求。EV出行时,如果发现自身电量不足,就会选择剩余电量可达的充电站进行充电,并且倾向于在前往目的地的途中“顺路”充电,考虑EV用户的出行需求可以最大化充电站服务的EV数量。
针对以上问题,本文结合出行链的概念,采用蒙特卡洛方法模拟大规模EV一周的出行活动及充电过程,EV个体根据自身的出行需求,以空驶成本和站内充电车流最小化为目标选择充电站,选择结果随充电站的布局动态变化,以此表征EV群体的充电需求。在此基础上,采用两阶段法制定充电站的规划方案,以EV群体空驶成本最小化为目标确定充电站站址,以充电站一周的最大充电负荷确定建设容量,最终选取建设成本最小和充电桩利用率最大的规划方案,兼顾运营商和EV用户的利益。最后,以一个典型城区为例进行仿真,验证了所提方法的有效性。
1 基于用户出行需求的EV充电负荷预测
单个EV充电需求的时空分布具有较大的随机性,但大规模EV群体的充电行为将呈现出规律性,分析EV充电需求的时空分布是充电站优化配置的基础。目前,预测EV充电需求的方法主要有排队论[5]、交通流量分布[9]和动态车流模拟[10]等,但上述方法均没有考虑EV用户的出行需求。一般而言,EV用户会根据出行目的地和出发地之间的距离及剩余电量来判断途中是否需要充电,并选择便捷的充电站。因此,EV的充电需求与出行需求密切相关。
1.1 基于出行链方式的EV出行需求分析
基于活动的出行链特征可以很好地描述用户的出行需求。出行链是指个人为完成一项或几项活动(多目的出行),在一定时间顺序上不同出行目的的连接形式[11]。出行链包括出行时间、出行目的、活动数量以及发生的顺序等特征,能够较好地模拟EV的出行过程以及EV充电需求的时空分布[12]。
按照活动类型可以将出行目的划分为回家H(Home)、工作 W(Work)、购物吃饭 SE(Shopping and Eating)、社交休闲 SR(Social and Recreational)和其他事务 O(Other family/personal errands)五大类[13],典型的出行链结构如图1所示。

图1 典型出行链结构Fig.1 Typical structures of trip chain
工作日和休息日EV的出行需求不同,本文以家为EV一天活动的起点和终点,工作日主要考虑以下3种活动行程:典型的两点一线式,如图1(a)所示;在下班途中进行SR/SE/O活动,活动结束后启程回家,如图1(b)所示;下班后先回家,再从家里出发去进行SR/SE/O活动,活动结束后启程回家,行程如图 1(a)、(c)所示。
对美国波士顿工作者的调查显示[14],下班途中停留1次的人约占24.1%,回家后出行1次的约占23.1%,因此,本文假设3种主要活动行程的概率分别为52.8%、24.1%、23.1%。
每种出行链的数据结构如式(1)所示:

其中,SL为出发地点;EL为目的地;ST为出发时间。
2009年,美国交通部对全美家用车辆的出行进行统计[15-16],统计结果显示,车辆第1次出行时刻和最后一次出行结束时刻均满足正态分布。因此,本文假设工作日中,EV用户的第1次出行时刻和下班时刻服从正态分布。
第1次出行时刻的概率密度函数如式(2)所示:

其中,μe=6.92;σe=1.24。
下班时刻的概率密度函数如式(3)所示:
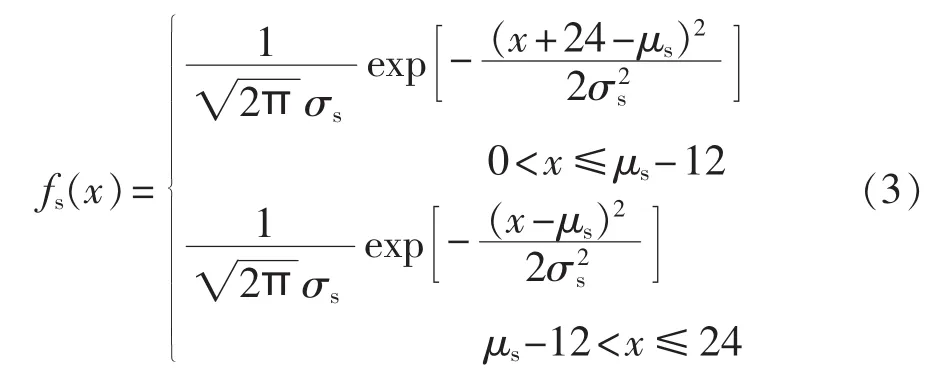
其中,μs=17.47;σs=1.8。
休息日主要考虑EV用户从家里出发进行SR/SE/O活动,结束后启程回家的行程,如图1(c)所示。休息日中,用户外出的概率为70%,其中35%的出行时间服从μe1=8.92、σe1=3.24的正态分布,35%服从μe2=16.47、σe2=3.41的正态分布。
1.2 EV充电需求分析
EV的剩余行驶里程Ls如式(4)所示:
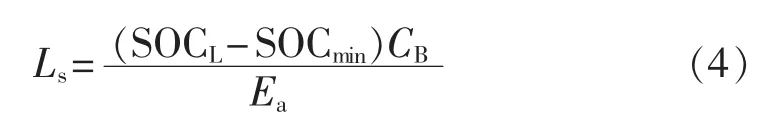
其中,SOCL为EV出行时的电池剩余容量;SOCmin为蓄电池的放电容量下限;CB为EV的蓄电池容量;Ea为EV每千米平均能耗。
EV用户根据自身的出行需求选定目的地,并计算出发点与目的地的最短路径距离,记为Lmin。假设各地停车场均已设有慢速充电桩,如果Ls>Lmin,则EV无需充电,可以根据最短规划路径直接前往目的地,到目的地再进行充电;否则,EV需要在行驶半径Ls内选取一个充电站进行快速充电,再前往目的地。本文主要针对一个城区进行仿真,假设EV通过一次充电后均可以到达目的地,暂不考虑EV长途行驶的情况。
为了减少EV的电量消耗,提高充电的舒适度,EV用户会选择空驶成本和车流量小的充电站进行充电。空驶成本指的是EV为了充电额外行驶的距离,EV从出发点直接到达目的地的行驶距离为LS-D,从出发点到达充电站i的行驶距离为LiS-C,从充电站i出发到目的地的行驶距离为LiC-D,则空驶成本最小化的目标函数如式(5)所示:

其中,SCS为EV剩余电量可达的快速充电站集合。
EV充电的舒适度主要与充电站的车流量相关,当站内车流过多时,容易造成拥堵和排队时间过长,降低EV充电的舒适度。车流量最小化的目标函数如式(6)所示:

其中,为向充电站i预约t时刻充电的 EV 数量函数;为用户出发到达充电站i的时间。
综合空驶成本最小化和充电车流量最小化的目标函数如式(7)所示:
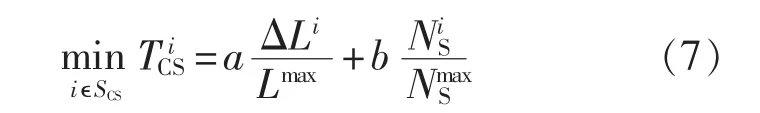
其中,a和b为权重系数,由用户的偏好所决定;Lmax为EV的续航里程;为充电站同时充电的EV数量最大值。
EV根据式(7)选定好充电站后,通过智能终端向充电站进行预约充电。EV群体充电需求的计算流程如图2所示。

图2 EV充电负荷计算流程Fig.2 Flowchart of charging load calculation
2 充电站选址定容模型
2.1 充电站选址模型
EV由于续航里程的限制,往往需要在行驶途中进行充电,充电站的选址会对EV的出行和空驶成本产生影响,如果充电站的分布不在EV剩余电量的可达范围内,一方面会对EV的出行带来不便,另一方面也会降低充电站的服务率,造成充电桩闲置。为了提高充电站的运营效益和EV充电的便利程度,本文以EV群体的空驶成本最小化为目标,以EV剩余电量可达为约束进行充电站选址,选址模型如下。
(1)目标函数。
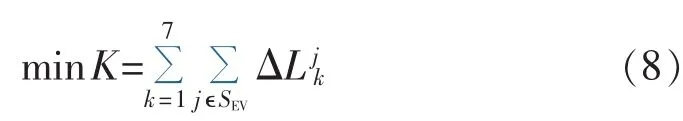
其中,SEV为EV群体组成的集合;为第j辆EV第k天选定最优充电站的空驶成本。
(2)约束条件。
为了满足EV的出行需求,必须保证具备一定初始电量的EV能够抵达充电站,约束条件如式(9)、(10)所示。式(9)要求EV出行时具有一定的初始电量,式(10)确保EV依靠剩余电量能够抵达充电站。
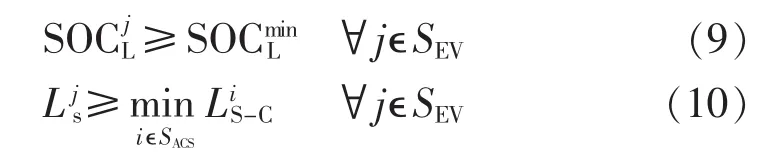
其中,为第j辆EV的初始电量为 EV初始电量的下限;为第j辆EV的剩余行驶里程;SACS为所有充电站组成的集合。
2.2 充电站定容模型
通常来说,充电站的规模越大,建设成本也越高,过大的容量规模会使站内充电桩出现闲置。但是,如果充电站的规模太小,就容易造成站内车流拥堵,EV的充电排队时间过长,降低EV用户的充电舒适度。因此,配置充电站的容量规模应该综合考虑EV用户的充电排队时间以及充电桩的利用率。
由于行驶中的EV充电需求比较急切,为了减少用户的充电排队时间,本文取一周内充电站的最大充电负荷为建设容量,同时考虑充电站的建设规模约束。站内充电桩的配置数量如式(11)所示,充电桩的利用率如式(12)所示。

其中,为站内充电桩配置的最大值;为充电站i的充电桩配置数量;为充电桩m一周内的有效工作时间,单位为h;ηm为充电桩m的利用率。
由于充电站建设规模的约束,有可能出现站内充电车辆的数量远大于充电桩的情况,为此,设置式(13)的约束条件,用于检验规划方案的可行性。
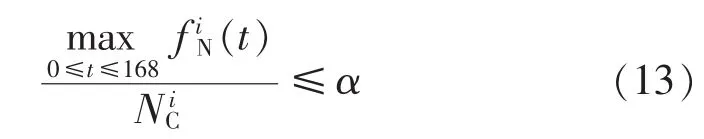
其中,α为站内充电车辆最大值与充电桩的比例上限,本文取为1.2。
3 模型求解方法
由于EV的出行具有随机性,难以用数学方法对此模型直接求解,本文采用蒙特卡洛方法对EV群体的出行需求进行模拟,并用遗传算法求取充电站的最优选址,充电站选址定容模型的求解流程如图3所示。
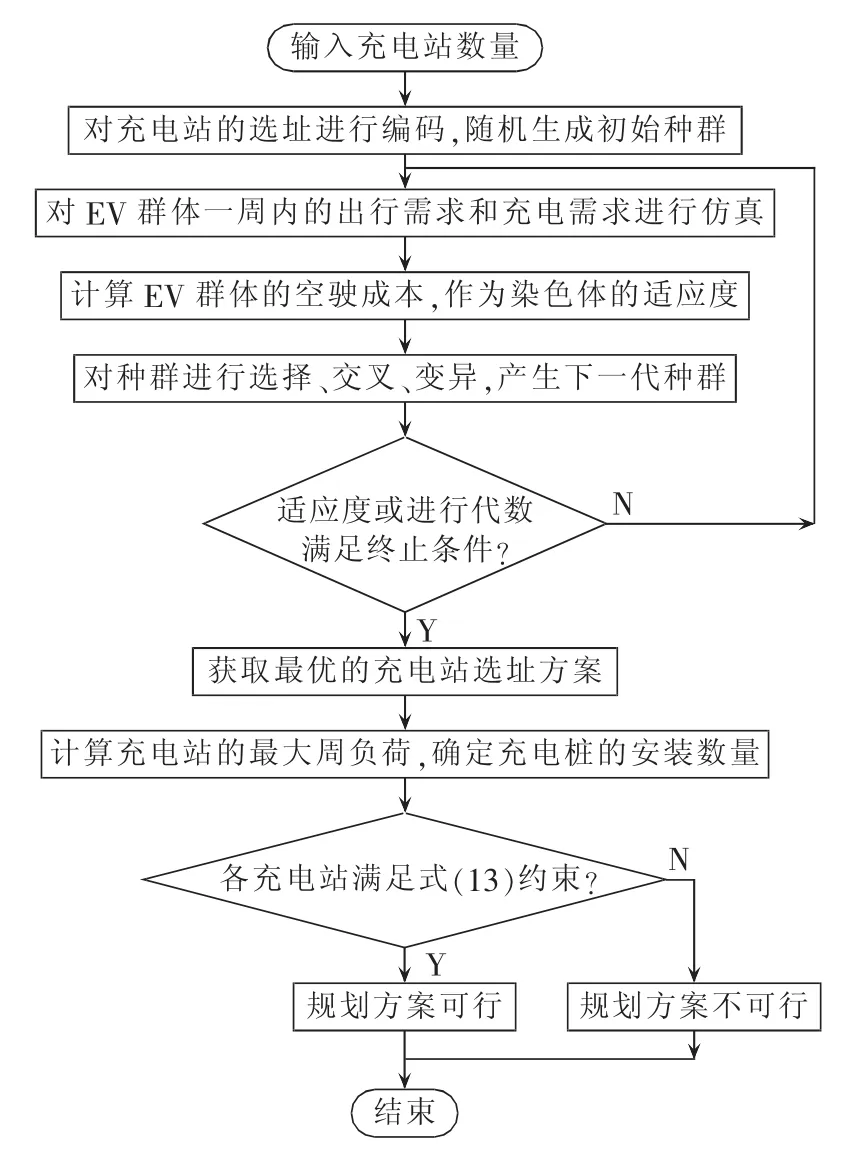
图3 充电站规划模型的求解流程Fig.3 Flowchart of charging station planning
4 算例分析
4.1 算例场景
本文针对一个典型的城区进行仿真分析,将整个仿真区域划分为居民区、商业区和工业区。如图4所示,线路中间的值为两节点间道路的距离,单位为km,拟建设快速充电站的地点为各道路交点。假设各地停车场均已建有充电桩,充电方式为慢充,EV在停车时可以进行充电,行驶途中的EV为了节省时间,充电时前往充电站,充电方式为快充。

图4 城区路网结构Fig.4 Urban road network structure
仿真区域内共有4000辆EV,参照日产Leaf的技术参数,EV的锂电池容量为24 kW·h,行驶100 km耗电量E100=15 kW·h,续航里程为160 km,快充时间为15min,充电功率为96 kW,EV的平均行驶速度va=40 km/h;过度的充放电均会缩短蓄电池的使用寿命,因此,将蓄电池的容量下限SOCmin设置为0.1,容量上限SOCmax设置为0.9,EV出行时电池的剩余容量 SOCL满足[0.8,0.9]的均匀分布,下班时满足[0.5,0.9]的均匀分布,;EV 选择充电站时,式(7)中 a=0.5,b=0.5,Lmax=160,。
各种活动类型中,H的地点为居民区;W的地点为工业区或商业区,工业区占80%;SR/SE/O的地点为商业区。EV用户出行时,根据出行活动的类型在不同的区域中随机选择目的地。EV用户工作日进行SR /SE/O 活动的持续时间满足[1,2]h的均匀分布,休息日满足[1,5]h的均匀分布。
4.2 充电站选址
基于遗传算法,求取快速充电站的最优选址方案。仿真结果表明,仅有2个充电站时,无法确保所有EV出行时均满足式(10)的约束;当建设7个充电站时,式(8)的目标函数值为0,可以实现所有EV的“顺路”充电。因此,充电站的可行建设数量为3~7个。不同充电站建设数量的选址方案见表1。
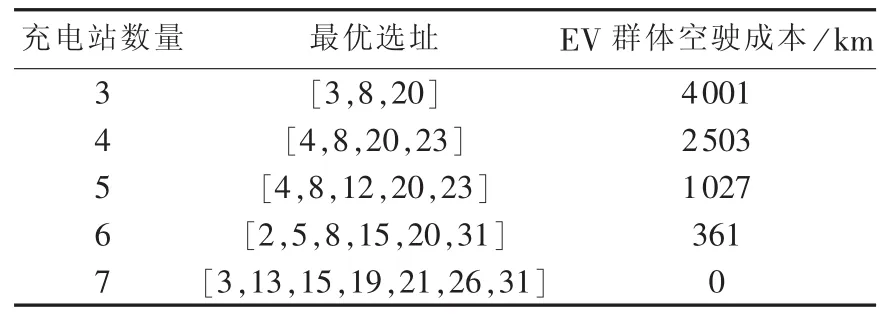
表1 充电站最优选址方案Table1 Optimal schemes of charging station planning
可以看出,充电站的最优选址主要分布在仿真区域中心附近的节点上,并且布局相对比较分散。随着充电站数量的增加,EV群体的空驶成本逐渐减少。
4.3 充电站定容
以EV群体的空驶成本最小化为目标得到充电站的选址方案后,运用蒙特卡洛方法对EV群体的出行需求进行模拟,获得各个充电站一周内的充电车流分布,由式(11)确定每个充电站的充电桩数量,判断是否满足式(13)约束,并根据式(12)计算充电桩的利用率。不同可行的规划方案所需配置的充电桩数量和充电桩利用率如图5所示。

图5 不同充电站数量的规划方案对比Fig.5 Comparison of planning scheme among charging station quantities
从图5可以看出,随着充电站数量的增加,所需的充电桩数量也逐渐增加,充电桩的利用率呈现下降趋势。从充电站投资建设的成本考虑,最优的充电站建设数量为3个,选址为节点3、8、20,分别配置 14、12、14 个充电桩,满足式(13)的约束,充电桩的平均利用率为28.05%,每天的平均有效工作时间为6.73 h。该方案下各充电站工作日的充电负荷分布如图6所示,从图6可以看出,3个充电站的充电负荷分配比较均衡,主要集中在用户下班以后。

图6 各充电站工作日充电负荷Fig.6 Charging load curve on working day for different charging stations
5 结论
本文提出一种基于用户出行需求的充电站规划方法。该方法结合出行链的概念,采用蒙特卡洛方法对大规模EV一周的出行活动及充电过程进行模拟。在规划充电站时,兼顾EV群体和电站运营商的利益,以EV群体空驶成本最小化为目标确定充电站站址,以充电站一周的最大充电负荷确定建设容量,最终选取建设成本最小和充电桩利用率最大的规划方案。通过仿真分析可以看出,充电站的合理规划,不仅能够提高充电设施的利用率,减少投资建设费用,还能满足EV用户的出行需求,为用户提供便捷舒适的充电服务,有利于EV的推广应用。
后续研究中,将进一步考虑规划区域道路的通行能力以及车流量对EV行驶速度和能耗的影响,使得EV充电需求时空分布的预测更为准确。
[1]苏海锋,梁志瑞.基于峰谷电价的家用电动汽车居民小区有序充电控制方法[J].电力自动化设备,2015,35(6):17-22.SU Haifeng,LIANG Zhirui.Orderly charging control based on peakvalley electricity tariffs for household electric vehicles of residential quarter[J].Electric Power Automation Equipment,2015,35(6):17-22.
[2]杨秀菊,白晓清,李佩杰,等.电动汽车规模化接入配电网的充电优化[J].电力自动化设备,2015,35(6):31-36.YANG Xiuju,BAI Xiaoqing,LIPeijie,et al.Charging optimization of massive electric vehicles in distribution network [J].Electric Power Automation Equipment,2015,35(6):31-36.
[3]陈思,张焰,薛贵挺,等.考虑与电动汽车换电站互动的微电网经济调度[J].电力自动化设备,2015,35(4):60-69.CHEN Si,ZHANG Yan,XUE Guiting,et al.Microgrid economic dispatch considering interaction with EV BSS [J].Electric Power Automation Equipment,2015,35(4):60-69.
[4]邵成成,王锡凡,王秀丽.发电成本最小化的电动汽车分布式充放电控制[J].电力自动化设备,2014,34(11):22-26.SHAO Chengcheng,WANG Xifan,WANG Xiuli.Decentralized EV charge/discharge controlwith minimum generation cost[J].Electric Power Automation Equipment,2014,34(11):22-26.
[5]葛少云,冯亮,刘洪,等.考虑电量分布及行驶里程的高速公路充电站规划[J].电力自动化设备,2013,33(7):111-116.GE Shaoyun,FENG Liang,LIU Hong,et al.Planning of charging stations on highway considering power distribution and driving mileage[J].Electric Power Automation Equipment,2013,33(7):111-116.
[6]NAKUL S,SCOTT K.An approach for the optimal planning of electric vehicle infrastructure for highway corridors[J].Transportation Research Part E,2013,59:15-33.
[7]熊虎,向铁元,荣欣,等.电动汽车电池更换站布局的最优规划[J].电力自动化设备,2012,32(9):1-6.XIONG Hu,XIANG Tieyuan,RONG Xin,et al.Optimal allocation of electric vehicle battery swap stations[J].Electric Power Automation Equipment,2012,32(9):1-6.
[8]曾正,赵荣祥,杨欢,等.电动汽车高渗透率的应对策略及换电站的最优规划[J].电力自动化设备,2012,32(9):7-13.ZENG Zheng,ZHAO Rongxiang,YANG Huan,et al.Responsive schemes to high penetration of electric vehicles and optimal planning of battery swap stations[J].Electric Power Automation Equipment,2012,32(9):7-13.
[9]王辉,王贵斌,赵俊华,等.考虑交通网络流量的电动汽车充电站规划[J].电力系统自动化,2013,37(13):63-69.WANG Hui,WANG Guibin,ZHAO Junhua,et al.Optimal planning for electric vehicle charging stations considering traffic network flows[J].Automation of Electric Power Systems,2013,37(13):63-69.
[10]刘洪,李荣,葛少云,等.基于动态车流模拟的高速公路充电站多目标优化规划[J].电力系统自动化,2015,39(24):56-62.LIU Hong,LIRong,GE Shaoyun,et al.Multi-objective planning of electric vehicle charging stations on expressway based on dynamic traffic flow simulation[J].Automation of Electric Power Systems,2015,39(24):56-62.
[11]褚浩然,郑猛,杨晓光,等.出行链特征指标的提出及应用研究[J].城市交通,2006,4(2):64-67.CHU Haoran,ZHENG Meng,YANG Xiaoguang,et al.A study on trip-chain indices and their application [J].Urban Transport of China,2006,4(2):64-67.
[12]温剑锋,陶顺,肖湘宁,等.基于出行链随机模拟的电动汽车充电需求分析[J].电网技术,2015,39(6):1477-1484.WEN Jianfeng,TAO Shun,XIAO Xiangning,et al.Analysis on charging demand of EV based on stochastic simulation of trip chain[J].Power System Technology,2015,39(6):1477-1484.
[13]陈丽丹,聂涌泉,钟庆.基于出行链的电动汽车充电负荷预测模型[J].电工技术学报,2015,30(4):216-225.CHEN Lidan,NIE Yongquan,ZHONG Qing.A model for electric vehicle charging load forecasting based on trip chains[J].Transactions of China Electrotechnical Sosiety,2015,30(4):216-225.
[14]BHAT C R.A comprehensive and operational analysis framework for generating the daily activity-travel pattern of workers[C]∥78th Annual Meeting of the Transportation Research Board.Washington DC,USA:[s.n.],2001:10-14.
[15]US Department of Transportation.2009 national household travel survey[EB/OL].[2014-10-05].http:∥nhts.ornl.gov/2009/pub/stt.pdf.
[16]许少伦,严正,冯冬涵,等.基于多智能体的电动汽车充电协同控制策略[J].电力自动化设备,2014,34(11):7-13.XU Shaolun,YAN Zheng,FENG Donghan,et al.Cooperative charging control strategy of electric vehicles based on multi-agent[J].Electric Power Automation Equipment,2014,34(11):7-13.

