基于H参数的换流器谐波全耦合模型

钟斌斌，李 妍，张永芳，陈 炜

（华中科技大学 电气与电子工程学院，湖北 武汉 430074）

0 引言

随着电力电子变换器装置广泛应用到电力系统中，直流与交流网络通过换流器相互耦合，换流器谐波源模型直接影响到谐波分析的正确性和准确性，成为目前学术界和工程界都非常关注的问题［1-4］。目前谐波分析中采用的换流器谐波源建模方法主要包括恒流源模型、Norton模型、谐波耦合导纳矩阵模型、开关函数模型等［5-6］。 文献［7］提出一个线性的简化模型来近似表示谐波源在基波电压初相位为零时的谐波特性，其各参数均需要通过多次实际运行测量数据进行最小二乘逼近建模，求取较困难，且谐波次数越高，谐波电流误差越大；文献［8］基于谐波耦合导纳矩阵，以解析方法推导晶闸管可控电抗器端口（交流侧端口）电压电流之间的耦合关系，并对交流侧谐波源模型进行了三方面的简化，具有较高的精度和适用性；文献［1，9］从工程实际出发，考虑触发角受余弦信号的调制，利用脉冲宽度调制和脉冲位置调制的频谱分析，运用转移函数法分析换流器两侧谐波分布，使工程实际中的谐波估算更加方便，结果更加精确；但上述建模方法均未对交直流两侧谐波相互耦合关系展开研究讨论。

文献［10-11］通过谐波传递函数矩阵和开关函数的方法建立谐波模型矩阵，研究交直流两侧谐波电压、电流之间的关系，但仅对单相换流器开展分析；类似地，文献［12-13］以三相整流桥为例建立谐波模型，对整流器两侧的交互作用进行分析，由于建模考虑触发角非对称，需通过牛顿-拉夫逊算法约束调整换相重叠角，该步骤需多次迭代计算整个参数矩阵，运算复杂，在应用于谐波分析时可能导致收敛困难。

考虑到电力系统中交流侧系统谐波电压幅值通常很小，不影响各开关器件的正常导通［14］，因此换流器触发角一般是对称的。本文基于二端口网络的H参数矩阵定量描述换流器交流侧电流与电压、交流侧电流与直流侧电流、直流侧电压与交流侧电压、直流侧电压与电流之间的耦合关系。通过将换流器各开关器件的动作状态分别以对应的开关函数表示，在触发角对称条件下分析各换流阶段换流器两侧电压电流的数学关系，并以傅里叶变换为工具求解各H参数矩阵，建立换流器谐波全耦合模型。本文模型可广泛应用于电力系统中存在各种背景谐波的交直流网络；当触发角较大，换相重叠角较小时，可忽略换相过程影响得出简化模型，适用于可控换流器触发角较大或者系统电抗较小的工程应用背景。Simulink时域仿真结果验证了建模工作的准确性。

1 换流器H参数谐波模型

1.1 H参数矩阵及其物理意义

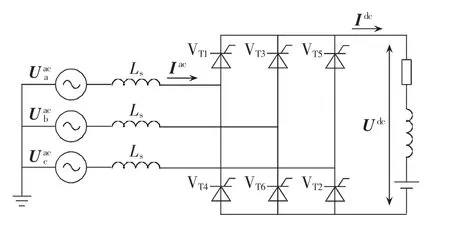
图1 三相换流器电路Fig.1 Circuit of three-phase converter

根据图1三相换流器电路，将其视为二端口网络，如图2所示，建立基于H参数的二端口网络方程（1）。

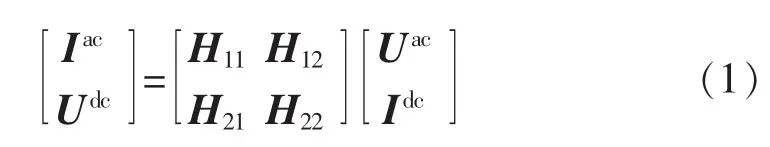
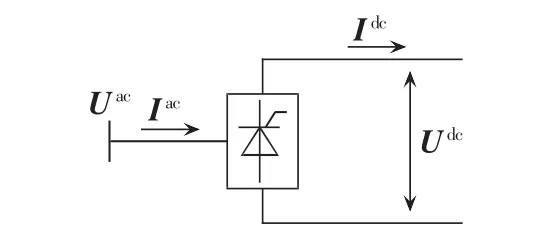
图2 换流器二端口网络Fig.2 Dual-port network of converter

通过H参数二端口网络方程（1）可直观地观察到，换流器两侧电压、电流之间的耦合关系可以用H参数矩阵表示，其中H11矩阵表示交流侧电流与电压之间的相互耦合关系，H12矩阵表示交流侧电流与直流侧电流之间的相互耦合关系，H21矩阵表示直流侧电压与交流侧电压之间的相互耦合关系，H22矩阵表示直流侧电压与电流的相互耦合关系。

本文研究三相换流器谐波模型，将式（1）扩展为三相换流器的H参数二端口网络方程（2），其中，H11扩展为3×3矩阵，即虚线左上角9个矩阵；H12扩展为3×1矩阵，即虚线右上角3个矩阵；H21扩展为1×3矩阵，即虚线左下角3个矩阵；H22矩阵依旧为1×1矩阵，即虚线右下角Hdd矩阵。以交流侧a相电流为例，矩阵Haa、Hab、Hac分别表示交流侧a相电流与交流侧a、b、c三相电压之间的相互耦合关系，矩阵Had表示其与直流侧电流之间的相互耦合关系。

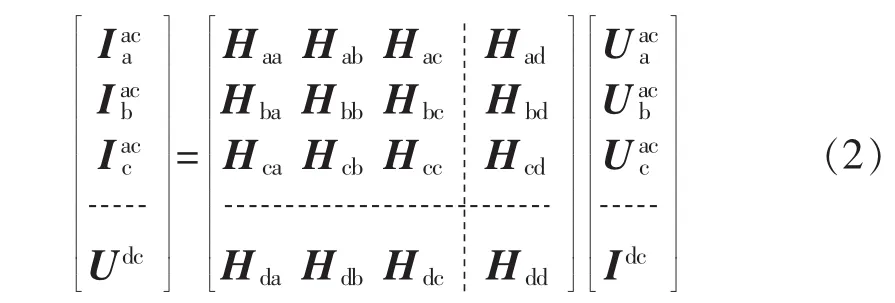
因此，通过求解上式16个H参数矩阵，三相换流器交直流两侧谐波的相互耦合关系可以定量地用二端口网络方程的H参数矩阵进行描述。

1.2 考虑换相过程的开关函数

为描述交直流两侧的谐波交互影响，本文将换流器开关器件的每个动作状态都通过一个开关函数进行描述，表示该区间内交直流两侧电压、电流的波形关系。如图3所示，将开关器件工作状态由开关函数Hx进行描述，即将电压、电流开关函数分解成多个Hx开关函数展开研究。其上标x表示此时工作区间内x号开关器件处于导通状态，例如H12表示此时换流器的1号和2号2个开关器件同时处于导通状态；H456表示此时有4号、5号和6号3个开关器件同时处于导通状态，即该区间为换相过程。

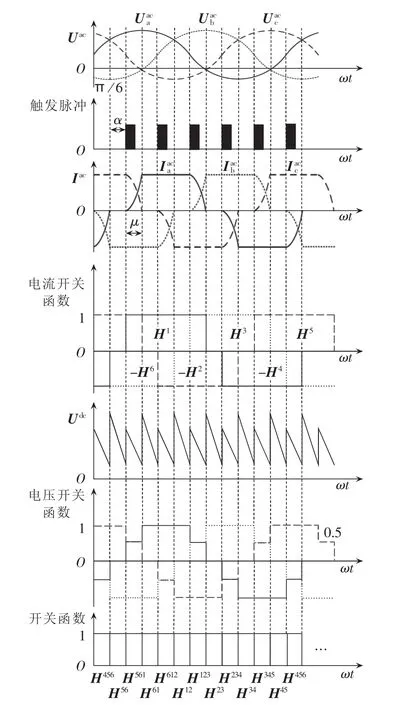
图3 开关函数原理图Fig.3 Schematic diagram of switching functions

1.3 指数形式傅里叶变换

为方便矩阵运算及直观体现谐波模型的作用机理，本文将各开关函数Hx以指数形式的傅里叶变换表示

以Ix=HxI为例，令其矩阵形式如式（3）所示，其中谐波傅里叶系数 hxn可通过式（4）求得［15］。

其中，θ、δ分别为Hx末端、始端相位。

可以看到，整个二端口网络方程中的H参数矩阵元素均为常数（仅与触发角、换相重叠角有关），而与换流器两侧交直流电压、电流无关。

2 换流器模型谐波分析

2.1 交流侧电流

根据图3中交流侧电流开关函数，其谐波分析可以在换流器截止、导通换相、导通和截止换相4个连续区间讨论，即为4个区间的各电流相量之和。以a相电流为例，其截止期间相电流为0；在导通换相、导通和截止换相期间，通过各区间的电流开关函数和交流侧电流线性组合，如式（5）所示。

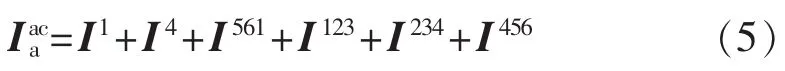
其中，I1和I4为导通期间电流，I561和I234为导通换相期间电流，I123和I456为截止换相期间电流，可由式（6）得到。

其中为换流器交流侧电流为各开关函数Hx所对应的区间内的交流侧电流。

2.1.1 导通期间交流侧电流

导通期间，由电流开关函数可知，交流侧电流等于直流侧电流，即得到：

根据上式分析可知，导通期间，交流侧电流仅与直流侧电流有耦合关系，且当直流侧电流中有谐波成分时，在交流侧将耦合产生除特征谐波以外的非特征谐波。

2.1.2 换相期间交流侧电流

根据图3中导通换相和截止换相期间的电流开关函数，换流器某相电流中一个开关器件导通换相期的开始同时伴随着另外一相电流中对应的开关器件截止换相期的开始，它们之间的电路等效关系如图4所示，其中电压、电流的上标“off”表示截止换相期，“on”表示导通换相期。

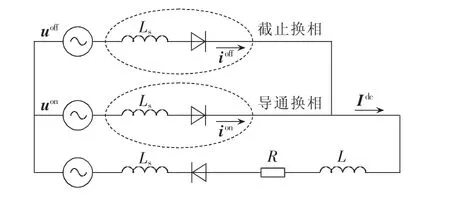
图4 换流器换相过程Fig.4 Commutation process of converter

根据图4电路换相过程中电压、电流关系，可得到其数学关系式如式（8）所示，且本文并未将换相过程进行线性化处理。

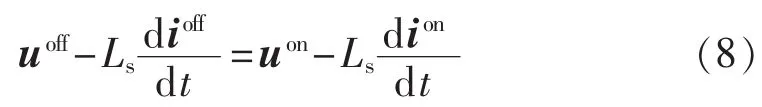
截止端换相电流ioff与导通端换相电流ion两者之和始终等于直流侧Idc；且ioff在换相初始相位（φc）时等于 Idc，ion在换相初始相位（φc）时等于 0。 得到截止换相处的交流侧电流表达式为：

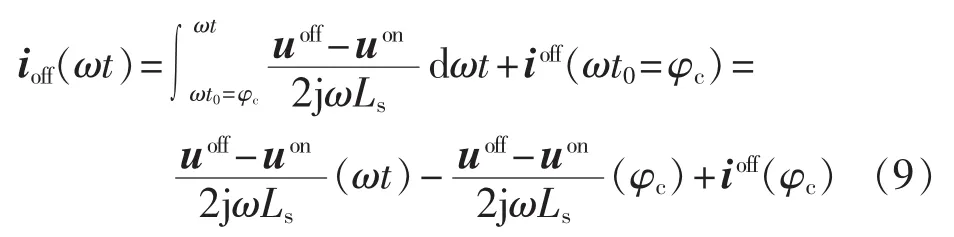
将式（9）以傅里叶级数指数形式表示：

得到截止换相电流ioff（ωt）的频域傅里叶系数为：

根据式（11）可知，截止换相过程中，交流侧电压与电流存在耦合关系，当交流侧电压含有系统谐波情况下，交流侧电流中将耦合产生相应的非特征谐波；另外交流侧电压和直流侧电流共同作用耦合产生直流成分。

将上式转换成矩阵形式：

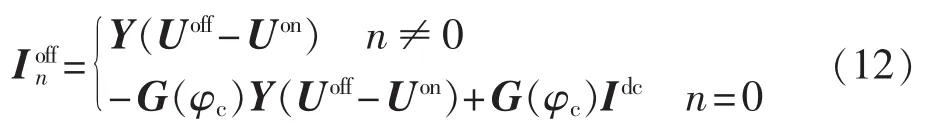
等效成：

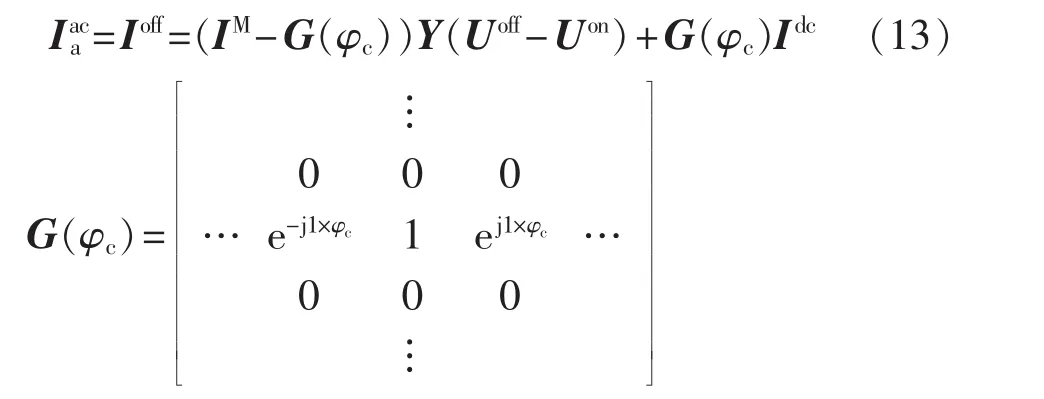
其中，IM为2n+1阶单位矩阵；为系统侧电抗的对角矩阵；φc为换相初始相位。

同理，可得导通换相电流ioff（ωt）频域矩阵形式：

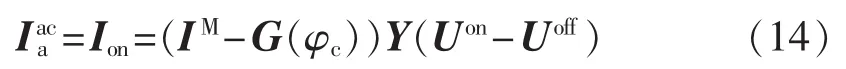
根据上式可知，导通换相过程：交流侧电压、电流存在耦合关系，当交流侧电压含有系统谐波情况下，交流侧电流中将耦合产生相应的非特征谐波。

2.1.3 谐波模型参数

综上，将各个区间对应的Iaca代入上式，得到换流器交流侧电流完整表达式。

以上表明交流侧电流与电压在换相期间存在耦合关系；在导通期间，交流侧电流与直流侧电流存在耦合关系。

将谐波模型矩阵式（2）与式（15）联立，即可得到换流器谐波模型矩阵中各个H参数矩阵：

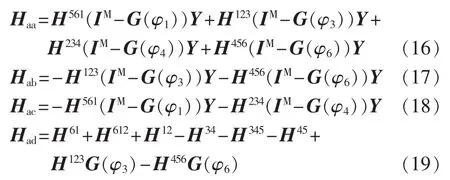
2.2 直流侧电压

根据图3中直流侧电压开关函数的描述，同样可以在截止、导通换相、导通和截止换相4个连续期间进行讨论，即通过幅值分别为0、0.5、1和0.5的水平线段进行近似［16］。以a相为例，其截止期间的直流侧电压为0；其他3个期间通过开关函数与其对应的交流侧电压（考虑系统电抗产生的压降后）线性组合得到直流侧电压，如式（20）所示［12］。

根据上式分析可知，直流侧电压与交流侧电压及直流侧电流均耦合，当忽略交流侧阻抗ZL产生的压降时，直流侧电压仅与交流侧电压耦合。

由谐波模型矩阵式（2）与式（20），即可得到换流器谐波模型矩阵中剩余各个H参数矩阵：

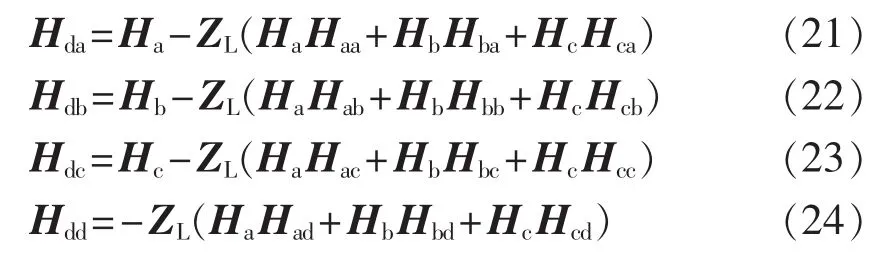
3 谐波简化模型

当换流器电路参数和触发角确定，其直流侧电流直流分量和换相重叠角μ分别为：

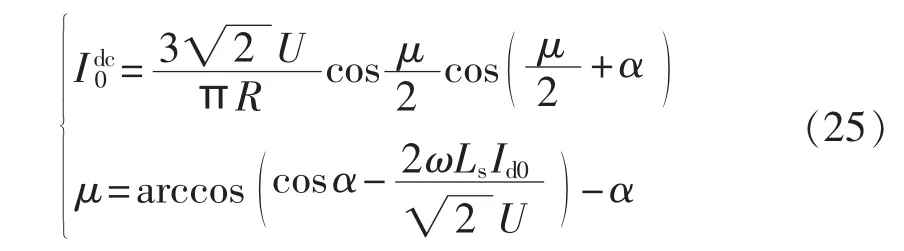
其中，U为交流侧线电压有效值；R为直流侧负载电阻；α为触发角；Ls为交流侧等效电抗；ω=2πf为角频率。

得到换相重叠角关于触发角及换流器电路参数的表达式：

根据式（26）和图5，当触发角（α＜90°）逐渐增大，换相重叠角将逐渐减小，相应的换相过程的开关函数区间减小，即换相过程对换流器谐波模型的影响减小。因此，当换相重叠角较小时，可不考虑换相过程的影响，谐波模型矩阵式（2）中左上角9个参数矩阵均为0矩阵，且其余7个参数矩阵也大幅简化，可将式（16）—（19）和（21）—（24）中换相过程开关函数（H561等）置0得到，得到简化模型矩阵式（27）。

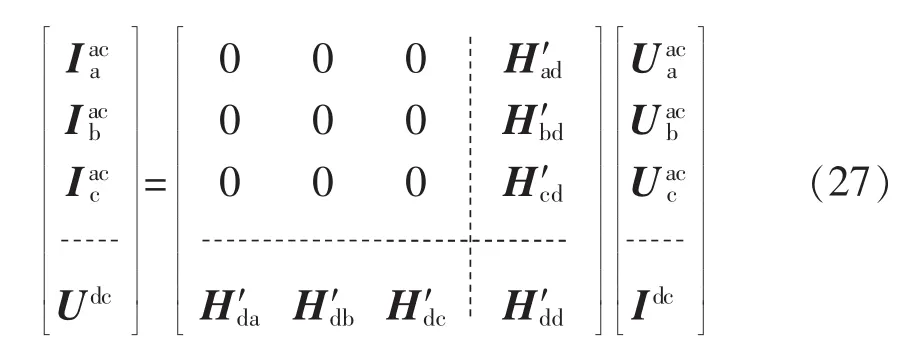
图5 换相重叠角与触发角关系曲线Fig.5 Relationship between commutation overlap angle and firing angle

从上述分析可知，当不考虑换相过程时，换流器简化谐波模型很大程度上简化了谐波模型，特别是交流侧电流与电压之间不存在耦合关系，交流侧电流仅与直流侧电流耦合。

4 算例仿真分析

本节通过对比本文建立的频域谐波模型和Simulink时域仿真结果，验证基于H参数的换流器谐波全耦合模型的准确性。由于本文重点研究换流器交直流两侧谐波交互作用机理，故在建模分析过程中认为换流器交流侧系统阻抗相等。算例采用三相全控整流桥，具体参数为：系统线电压有效值为400 V，交流侧电感Ls=0.2 mH，直流负载侧电阻R=5 Ω，负载电感L=0.5 H。

4.1 无系统背景谐波情况

当不存在系统背景谐波，即理想环境下，本文建立的谐波模型及其简化模型和Simulink时域仿真得到两侧谐波幅值对比如表1所示。

由表1结果可知，本文所建立的换流器谐波模型在无背景谐波情况下换流器两侧的特征谐波幅值与时域仿真结果基本一致，误差较小；另外，随着触发角增大，本文简化谐波模型的精确度有较大提高；可以预见当触发角增大到一定程度时，该简化模型将有很强的实用性。

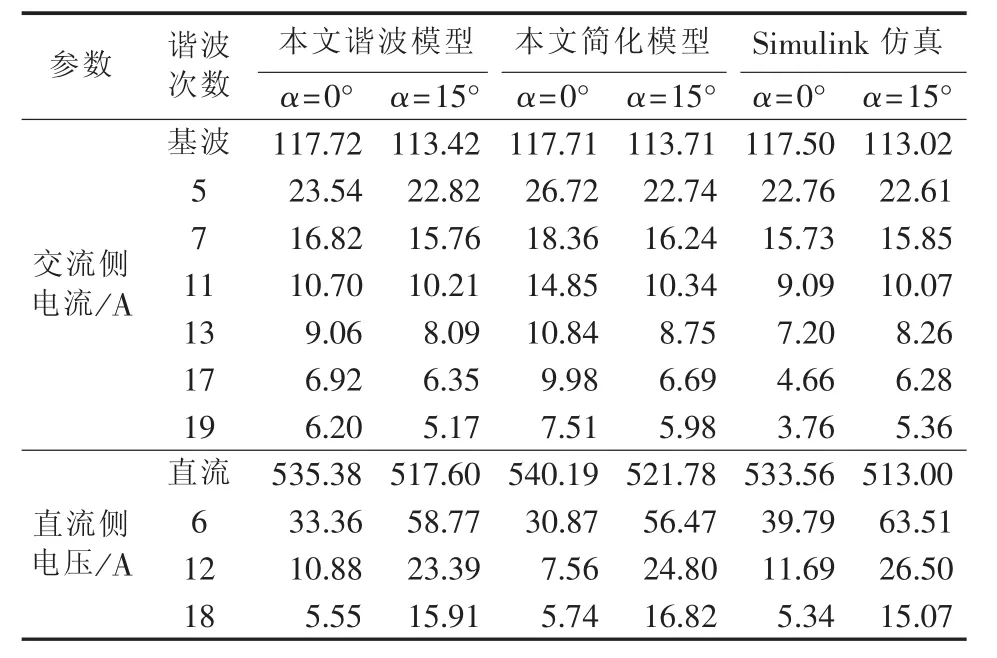
表1 无背景谐波情况下换流器两侧谐波幅值Table1 Amplitude of harmonics at both sides of converter without background harmonics

根据表2可知，在本文算例设定条件下，当触发角大于30°时，简化模型交流侧电流总谐波畸变率（THD）和直流侧电压纹波系数（RF）均与仿真结果接近，可建议采用简化模型展开分析研究。

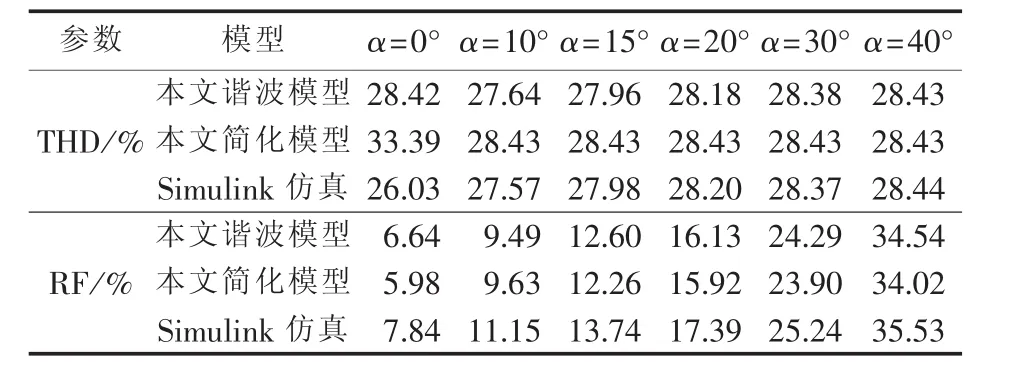
表2 电流总谐波畸变率与电压纹波系数结果分析Table 2 Analysis of current THD and voltage RF

4.2 有系统背景谐波情况

当考虑系统含有背景谐波，假设三相供电电源A相发生谐波畸变，含有5次正序谐波电压，幅值为系统相电压的5%；且负载直流侧电流中亦发生畸变，含有5次正序谐波电流，其幅值为直流电流的5%，此时取触发角为15°。

考虑主导非特征谐波，交流侧正序h次谐波扰动，将在直流侧产生h±（6k±1）次谐波；直流侧h次谐波扰动将在交流侧产生 h±1 次谐波［14，16］。 按照上述分析，本算例应在特征谐波的基础上在交流侧产生 3、4、6、9、15、…次非特征谐波扰动；在直流侧产生 4、8、10、14、16、…次非特征谐波。

本文谐波模型及其简化形式和时域仿真结果的谐波频谱见图6、7。可见，交直流侧电压、电流各谐波次数与理论分析及时域仿真一致，且各谐波幅值误差较小，可以验证本文谐波全耦合模型对分析换流器交、直流两侧谐波全耦合具备有效性和准确性。

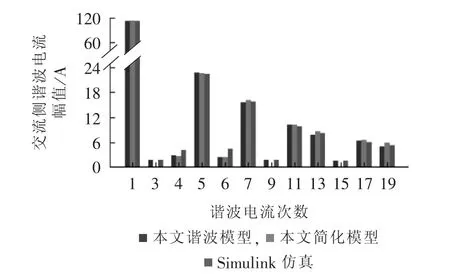
图6 有背景谐波情况下交流侧电流谐波频谱Fig.6 Harmonic spectrum of AC-side current with background harmonics

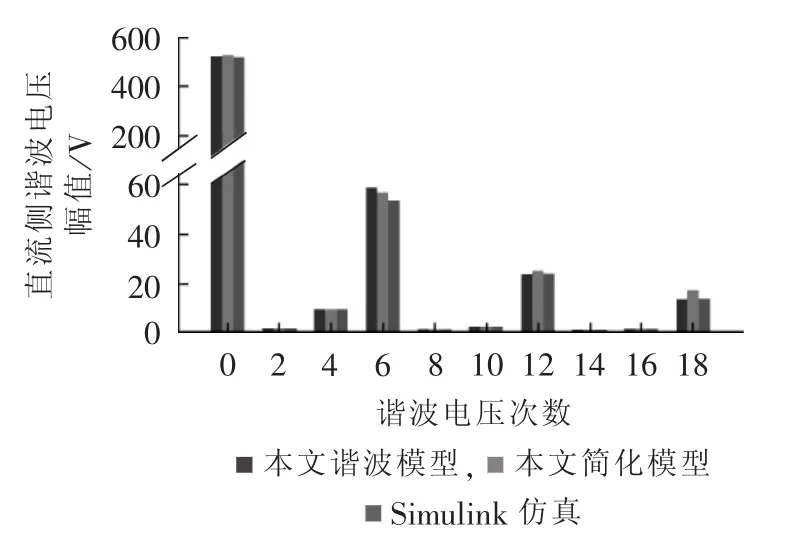
图7 有背景谐波情况下直流侧电压谐波频谱Fig.7 Harmonic spectrum of DC-side voltage with background harmonics

5 结语

本文通过引入二端口网络的H参数矩阵，将换流器各开关器件的动作状态分别以对应的开关函数表示，在触发角对称条件下分析各换流阶段交直流两侧的电压电流数学关系，并以傅里叶变换为工具求解各H参数矩阵，建立谐波全耦合模型。各H参数矩阵定量地描述了换流器交流侧电流与电压、交流侧电流与直流侧电流、直流侧电压与交流侧电压、直流侧电压与电流之间的耦合关系。本文谐波模型对存在各种复杂背景谐波状况的交直流系统均可适用；当触发角较大、换相重叠角较小时，可不考虑换相过程的影响，得到简化模型，适用于可控换流器触发角较大或系统电抗较小的工程应用背景。最后在Simulink时域仿真中验证了本文模型的准确性。

［1］JOS A，NEVILE R W.Power system haromics［M］.2nd ed.Chichester，UK：John Wiley&Sons，Ltd.，2004：143-187.

［2］赵伟，姜飞，涂春鸣，等.电动汽车充电站入网谐波分析［J］.电力自动化设备，2014，34（11）：61-66.ZHAO Wei，JIANG Fei，TU Chunming，et al.Harmonic current of grid-connected EV charging station［J］.Electric Power Automation Equipment，2014，34（11）：61-66.

［3］王中，孙元章，李国杰，等.双馈风力发电机定子电流谐波分析［J］.电力自动化设备，2010，30（6）：1-5.WANG Zhong，SUN Yuanzhang，LI Guojie，et al.Stator current harmonics analysis of doubly-fed induction generator［J］.Electric Power Automation Equipment，2010，30（6）：1-5.

［4］史丹，任震，余涛.高压直流输电系统的谐波分析方法综述［J］.电力自动化设备，2006，26（4）：93-97.SHI Dan，REN Zhen，YU Tao.Overview of harmonic analysis methods in HVDC transmission systems［J］.Electric Power Automation Equipment，2006，26（4）：93-97.

［5］BURCH R，CHANG G，DWYER R，etal.Characteristicsand modeling of harmonic sources-power electronic devices［J］.IEEE Transactions on Power Delivery，2001，16（4）：791-800.

［6］郑连清，吴萍，李鹍.电力系统中谐波源的建模方法［J］.电网技术，2010，34（8）：46-50.ZHENG Lianqing，WU Ping，LIKun.Modeling approachesof harmonic sources in power system［J］.Power System Technology，2010，34（8）：46-50.

［7］赵勇，张涛，李建华，等.一种新的谐波源简化模型［J］.中国电机工程学报，2002，22（4）：47-52.ZHAO Yong，ZHANG Tao，LI Jianhua，et al.A new simplified harmonic source model for harmonic analysis and mitigation［J］.Proceedings of the CSEE，2002，22（4）：47-52.

［8］孙媛媛，徐文远.整流器的谐波分析方法［J］.电力自动化设备，2009，29（3）：10-15.SUN Yuanyuan，XU Wenyuan.Harmonicanalysismethodfor converter［J］.Electric Power Automation Equipment，2009，29（3）：10-15.

［9］刘宏，焦连伟.转移函数应用于变流器的谐波分析［J］.电工技术学报，2005，20（9）：108-113.LIU Hong，JIAO Lianwei.Harmonic hnalysis using transfer function on the converter［J］.Transactions of China Electrotechnical Society，2005，20（9）：108-113.

［10］JALALI S G，LASSETER R H.Harmonic interaction of power systems with static switching circuits［C］//Power Electronics Specialists Conference，22nd AnnualIEEE.Cambridge，MA，UK：［s.n.］，1991：330-337.

［11］SASAN G J，ROBERT H L.A study of nonlinear harmonic interaction between a single phase line-commutated converter and a power system［J］.IEEE Transactions on Power Delivery，1994，9（3）：1616-1624.

［12］RAJAGOPAL N，QUAICOE J E.Harmonic analysis of threephase AC/DC converters using the harmonic admittance method［C］//Electricaland ComputerEngineering.Vancouver，BC，Canada：IEEE，1993：313-316.

［13］GUTIERREZ O，FUERTE-ESQUIVEL C R，RUBIO J A，et al.Harmonic analysis of AC/DC systems based on phase-domain multi-port network approach［J］.Electric Power Systems Research，2008，78（10）：1789-1797.

［14］徐政.交直流电力系统动态行为分析［M］.北京：机械工业出版社，2005：76-87.

［15］EDWARD W，KAME N，BONNIE S H.信号与系统基础——应用 Web和 MATLAB［M］.2版.北京：科学出版社，2007：145-160.

［16］李琼林，刘会金，刘云.三相变流器的谐波/间谐波统一调制分析建模［J］.高电压技术，2008，34（4）：91-95，100.LI Qionglin，LIU Huijin，LIU Yun.Uniform modulation modeling of three-phase converter for the analysis of harmonic/interharmonic［J］.High Voltage Engineering，2008，34（4）：91-95，100.