改善多馈入直流系统电压无功特性的直流控制策略

李 妮 ，李兴源 ，冯 明 ，肖 俊 ，洪 潮

（1.四川大学 电气信息学院，四川 成都 610065；2.中国南方电网有限责任公司 电网技术研究中心，广东 广州 510080）

0 引言

随着我国直流输电规模的快速增长，单个直流输送容量的增加和多馈入受端结构的形成，电网“强直流弱交流”特点逐渐明显。南方电网作为典型的多馈入受端系统，具有负荷密集、感应电动机比例较高的特点。在这种情况下，受端交流系统发生故障可能导致多回直流同时换相失败，并产生复杂的交直流相互作用，使得系统动态无功需求剧烈变化；同时，由于直流落点处的负荷中心地区缺乏电源支撑，动态无功缺乏，交流系统严重故障时电压稳定问题突出，威胁着系统安全［1-2］。因此，合适的直流控制技术与动态无功补偿技术对解决受端系统电压稳定问题有着关键的作用［3-6］，利用直流系统本身的无功调节能力相较于装设无功补偿装置而言，是一种更为经济的手段。

目前基于换流站控制改善交流系统无功特性的控制系统大致分为2类：一类以交流系统无功功率交换量为控制对象，将换流器与交流系统交换的无功功率控制在一定的范围内；另一类是以换流母线电压为控制对象，以维持交流电压稳定进行换流站无功调节［7-10］。针对多馈入系统的无功调节措施，较多采用第二类，文献［9］提出基于交流电压偏差变化的熄弧角无功调节方法，由于该方法受制于熄弧角，无功调节对受端电压稳定作用有限，仅针对过电压的情况。文献［10］设计的协调控制器中提出定交流电压控制，能够在加快系统恢复的同时有效改善交流母线电压稳定性，但该方法的理论研究及可行性有待进一步研究。

基于上述研究，本文从换流器运行特性的角度，分析了定交流电压控制对无功功率的调制作用，结合多馈入系统结构及电压的评估指标，提出了该控制方式在逆变侧的配合及设置策略，对受端电网换流母线电压稳定问题及动态无功缺乏问题具有一定的改善作用。最后通过算例分析，验证了该控制方案的有效性及可行性。

1 定交流电压控制特性

定交流电压控制属于直流站控制，其实质是通过调节换流器与交流系统的无功功率交换，控制换流站内交流母线的电压特性［11］。文献［12］通过仿真研究证明了该控制方法对多馈入系统恢复期间的电压波动和后继换相失败有一定程度的抑制作用。本文从逆变器运行范围的角度对定交流电压特性进行分析。

稳态运行时，逆变器有功和无功功率的运行范围可由Pn-Qn坐标系统表示［13］，如图1所示。以流向直流系统的功率方向为正，定直流电流Id特性是以原点为圆心的圆，需在最大电流Idmax与最小电流Idmin这2个圆弧之间变化；定直流电压Ud特性是通过原点的直线，它与运行功率Pn轴的夹角为功率因数角φ，Ud可在0～Ud0范围内调节；定熄弧角γ特性为一条下凸曲线，变化范围在γ≥γ0（γ0为允许运行的最小熄弧角）内。因此逆变器的运行范围实际是限制在定 γ0特性曲线、Idmax和Idmin圆弧以及 Ud=0所围成的封闭区域内。图中，e为逆变器额定运行点；Pde为额定输送功率；φ0为额定功率因数角；Ud0为逆变侧空载直流电压。由图1可知，若逆变器不限于定熄弧角运行，在保持额定直流功率不变的情况下，其无功功率可沿线1进行调节，由Idmax与γ0分别限制最大与最小可调量。该图表明，充分利用逆变器的无功功率调节能力，可以在一定程度上解决换流站内无功功率平衡问题，尤其是与弱交流系统相连的换流站。

图1 逆变器运行范围Fig.1 Operating range of inverter

当逆变器采用定交流电压Ui控制时，一般情况下，整流器采用定电流控制，可以维持逆变器的视在功率Si不变，运行特性与定直流电流重叠，如曲线2，在额定运行点e处与定熄弧角特性相交。已知逆变器控制运行与功率因数的关系为：

当交流系统受到扰动，母线电压Ui呈下降趋势。当逆变器采用定熄孤角控制时，如式（1）所示，为了维持γ恒定，使控制角β增大，功率因数角φ增大，即图1中运行点沿曲线3偏移至点e′0，逆变器消耗的无功功率Qn增加，导致Ui进一步下降；当逆变器采用定交流电压控制时，为了维持Ui在整定值内恒定，逆变器快速调节控制角，即使β减小，φ减小，运行点沿e′1方向移动，逆变器消耗的无功Qn减小。

如图1所示，在逆变器运行范围内，定交流电压控制与定熄弧角控制的无功功率特性分别为曲线2与曲线3。当系统轻载运行时，定交流电压控制将增大换流器无功功率吸收，维持交流母线电压为整定值；定熄弧角控制则需通过切电容器、静止无功补偿器增发感性无功等来调节过剩的无功功率，调节量由曲线2与3的纵坐标差决定，当Pn=0.8Pde时，无功功率调节量约0.4Pde。由此可见，相比定熄孤角控制，定交流电压控制具有更有利于控制无功功率、稳定母线电压，在适宜情况下可作为改善弱交流系统电压稳定性的经济控制技术。

2 多馈入系统电压稳定评估计算

2.1 电压稳定耦合因子的定义

落点较近的多馈入直流系统，换流站交流母线的电气联系较强，其间的相互作用可能导致系统总体性能下降［14］。因此衡量换流母线电压的稳定性，需要同时考虑系统的自身强度以及直流间的耦合影响［15］。

电压稳定因子（VSF）是衡量电压稳定性的经典判据之一，它代表节点电压对注入无功扰动的灵敏度［16］。由于其物理意义明确，该指标同样适用于多馈入系统，衡量直流输电中换流母线电压稳定性。

已知简单多馈入模型如图2所示，对系统i而言，VSFi的定义如下：

其中，VSFi为正表示系统静态电压稳定，其值越小越稳定，越大则稳定性越弱。从定义上看，该指标重点考虑了节点自身处的电压稳定，没有突出直流间的相互作用。

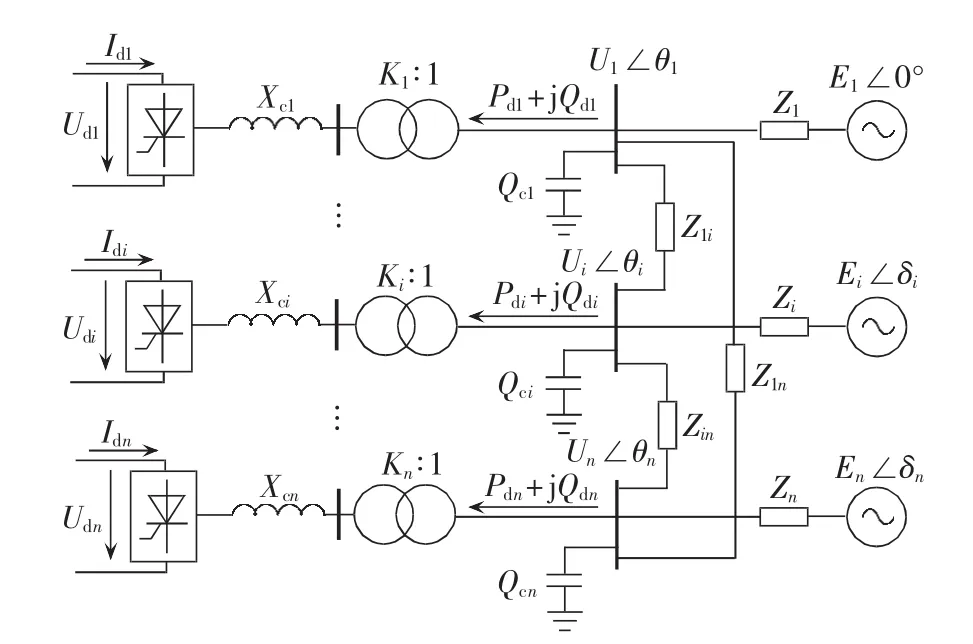
图2 多馈入直流系统简化模型Fig.2 Simplified model of multi-infeed HVDC system

利用多馈入交互作用因子（MIIF），能够定量描述两换流母线间电压相互影响的程度［17］，即母线i对母线j的交互作用因子MIIFji可表示为：

其中，为定义表达式，指在换流母线i处投入对称三相电抗器引起1%的电压波动ΔUi时，换流母线j的电压变化率；为结构表达式，其中Zeqij、Zeqii分别代表保留换流母线的节点阻抗矩阵Zeq中互阻抗与自阻抗元素。不论在定义式还是结构式中，均可看出交互作用因子指标表征了直流i对直流j的参与度。

综上分析，假定在母线i处投入三相电抗器，产生无功扰动（记为ΔQi），i的电压波动可记为：

根据两节点间的交互关系，ΔUi使得母线j产生的电压变化为：

同理，由式（6）可定义多馈入系统中，某一换流母线 i发生无功扰动 ΔQi（i=1，2，…，n；i≠j）时，母线j的电压稳定因子为：

综上，为了衡量某一换流母线电压受到所有与其相连的直流系统无功波动的影响，可定义节点j的电压稳定耦合因子（VSIF）为：

对于n馈入的直流系统，VSIFj的含义为：依次在换流母线 i（i=1，2，…，n；i≠j）注入无功功率，而引起1%的电压波动时，母线j的电压稳定程度之和。

在多馈入交直流系统中，换流母线节点j的电压耦合因子VSIFj越大，则说明该母线电压受其他节点无功扰动的影响越大。在动态无功缺乏的情况下，其他节点发生故障可引起该母线电压较大幅度的波动，同时增加了换相失败的风险［18］。

2.2 电压稳定耦合因子的计算方法

下面将通过解析法对电压稳定耦合因子进行求解分析［20］。

如图2所示的多馈入系统，其线性化潮流形式可表示为：

其中，ΔP、ΔQ为母线注入功率的增量；J为2n×2n阶的雅可比矩阵。

由于换流站注入节点的直流功率变化量仅与当地电压幅值相关，与交流系统电压相角无关。对式（9）中的直流量进行修正，有：

其中，ΔP′、ΔQ′为不包含换流站注入节点的直流功率增量；J′PU、J′QU分别为 JPU、JQU对角线元素的修正矩阵。修正元素为：

令 ΔP=0时，根据文献［19］可知 ΔQ与 ΔU的关系为：

由电压稳定因子的定义式可知：

根据式（12）、（13）可知，电压稳定耦合因子同样可表示为：

由式（14）可知，电压稳定耦合因子为降阶雅可比矩阵J-1R第j行除对角元素的和值，其值决定了换流母线电压交互耦合的强度。可以看出，电压稳定耦合因子与直流系统、受端交流系统的结构参数密切相关。

3 控制策略的实现

3.1 定交流电压控制的配合方式

逆变侧控制是由多个控制器相互配合组成，通常以某一控制器为主要调节，其余控制器作为附加调节。定交流电压控制无论设为主控制或附加控制，都是通过调节β角控制逆变器无功消耗来维持换流母线电压稳定。若将定交流电压控制设为主控制器，直流电压将运行在较大的范围，分析如下。

定交流电压控制的稳态运行特性为：

设在直流控制作用下Ui与Id保持恒定，认为叠弧角μ不变，由式（16）可知直流电压将随β变化而波动，已知 β∈（30°，90°），将式（15）代入式（16），求Ud对β的偏导为：

由系统运行状态易知 A1＞0，A2＜0；稳态中β 维持在较小的角度，Ud随β的上调呈减小趋势。考虑到直流输电工程中，由投切无功装置等引起换流母线无功扰动频繁，易使Ud低于额定运行点运行，从而增加有功功率的传输损耗，影响运行的经济性。然而，为了解决传统定熄弧角控制方式在扰动期间使功率因数下降，不利于电压稳定，易导致弱受端系统电压崩溃的问题，定交流电压控制更加适合作为定熄弧角控制的附加控制。其原理框图如图3所示。

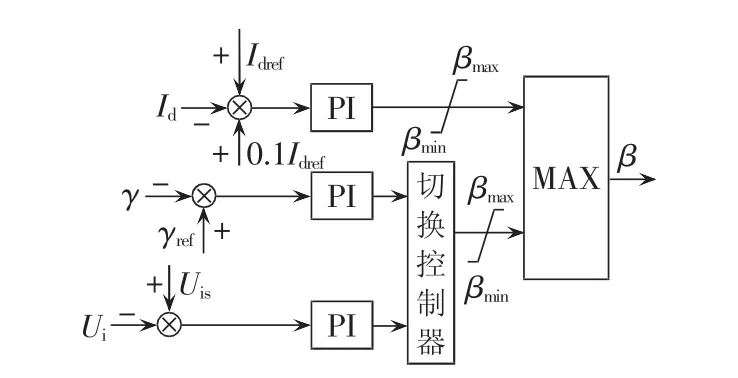
图3 定交流电压控制原理框图Fig.3 Schematic diagram of constant AC voltage control

3.2 平滑切换逻辑控制器设计

为了避免噪声干扰和瞬时小扰动引起不必要的控制动作，切换控制器通常需要满足一定的切换条件［10］，实现逆变器控制方式的平滑转换。

由于常规定熄弧角控制与附加定交流电压控制器参数配置的不同，在定交流电压控制接收指令退出控制时，2种控制方式存在微小的控制量（β）差，在系统恢复稳态后，简单的切换动作也可能引起较大的振荡。为了避免对系统的再次干扰，本文设计了基于状态跟随的平滑切换控制方法，其原理如图4所示。

图4 平滑切换逻辑控制器原理框图Fig.4 Schematic diagram of smooth logic switchover controller

将定交流电压控制状态与定熄弧角控制状态设计为一负反馈，作为定熄弧角的一个输入，使得暂态过程中定熄弧角随时跟随定交流电压输出，保证切换前2个控制器输出的状态量总是一致。同时对逻辑开关K1—K4进行合理的控制实现。

（1）系统稳态时：K2、K3闭合，K1、K4断开；逆变侧运行在定熄弧角控制方式下，隔离定交流电压控制。

（2）定交流电压控制时：K1、K3、K4闭合，K2断开；扰动期间，定熄弧角闭环控制器的状态量将跟随定交流电压控制器输出，此时逆变侧的控制是以换流母线电压为主要调制对象的控制作用。

3.3 控制器参数寻优算法

为了满足逆变侧定交流电压附加控制器的性能要求，本文采用非线性规划SIMPLEX算法对附加控制器参数KP、KI进行优化。

非线性规划数学模型的一般形式为：

设R是满足上式约束条件gj（X）的n维欧氏空间En中的一个开集，则多元函数f（X）最小极点存在的必要条件为：f（X）在R上有二阶连续偏导数，对于 X*∈R，若Δ f（X*）=0 且二阶偏导数矩阵（Hessian矩阵正定，则 X*∈R 为 f（X）的严格局部极小点。

在规划式（20）的求解过程中，搜索方向的确定及迭代步长的选择是优化算法的关键，由于SIMPLEX算法对初值敏感且易陷入局部最优，本文参数优化迭代过程分为初值搜索迭代和优化迭代：首先以较大步长和较小数值仿真次数得到SIMPLEX迭代初值，然后利用SIMPLEX算法在较小的步长范围内得到最优解。本文在PSCAD程序中，分别由Multirun模块与Simplex模块来实现上述步骤。

设目标函数满足换流母线实际电压Ui与整定值Uref的偏差最小，为：

寻优控制器参数KP、KI的步骤如下。

a.给定初值 X0=［KP0KI0］及可行域 R。

b.确定搜索方向Dk与步长λk，使迭代满足：

c.初步求得可行域最优解，得到SIMPLEX算法初值 X（0）。

d.设定优化次数N，利用SIMPLEX求解目标函数。

e.迭代结束，得到最优解 KP、KI。

4 控制策略的仿真研究

4.1 系统模型

为了验证本文提出的直流控制策略效果，基于CIGRE直流输电标准测试模型搭建了三馈入直流系统，结构如图2所示。每条直流线路的系统参数及无功补偿参数与CIGRE标准系统参数相同。通过改变等值阻抗Z1、Z2、Z3或联络线距离可以得到不同交流系统强度和电压稳定交互因子的多馈入系统。 设Z1=4.996+j14.5852Ω，Z2=4.75+j13.414 Ω，Z3=5.7906+j20.457 Ω，各直流系统逆变侧的电气距离为 l12=50 km、l13=80 km、l23=30 km，得到系统电压评估指标如表1所示。联络线阻抗为0.41 Ω/km，X /R＝6。

表1 系统电压评估指标Table 1 Evaluation indexes of system voltage

由表1可以看出，多馈入有效短路比（MESCR）与电压稳定因子对换流母线电压稳定特性的评估结果一致，由弱到强依次为：DC3、DC1、DC2。 根据电压稳定耦合因子的大小，各母线电压受耦合影响，由大到小依次为：DC2、DC1、DC3。上述指标表明，DC3换流母线的电压稳定性最弱；DC2母线电压受到的耦合作用最大，由于与DC2相连的DC1、DC3系统强度相对较弱，其受联络线无功波动产生的不利影响也将最大。因此从改善系统整定电压稳定性角度出发，对DC3、DC2逆变站装设定交流电压附加控制。

4.2 仿真结果

为了验证上述控制方案的效果，考察最弱系统DC3逆变侧换流母线处发生三相短路故障，故障持续时间0.05 s，DC3、DC2系统加入定交流电压附加控制时，各直流系统的电压恢复特性如图5所示（交流母线电压 Uac、直流电压 Ud、直流电流Id均为标幺值）。

由图5可见，在常规定熄弧角控制作用下，弱交流系统发生的严重故障对多条直流系统的电压稳定性产生了不利影响：随着DC3换流母线电压骤降至 0.4 p.u.，DC1、DC2系统交流母线电压被迅速下拉至0.85 p.u.，直流电压分别跌落至0.72 p.u.与0.26 p.u.，3条直流逆变侧同时发生换相失败；故障清除后，由于常规定熄弧角控制的超调作用，换流站功率因数暂时大幅减小，造成逆变侧无功功率的剧烈交换，各母线电压波动严重，尤其是电压稳定耦合因子最大的DC2系统与弱系统DC3都出现了后继换相失败。

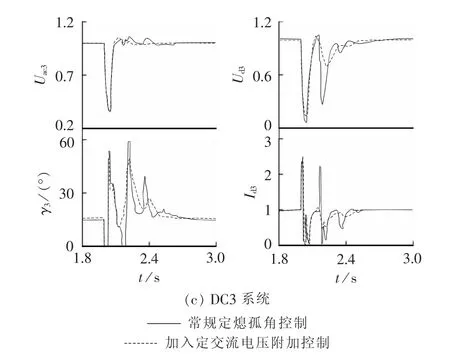
图5 定交流电压控制对换流母线电压特性的影响Fig.5 Influence of constant AC voltage control on voltage characteristics of commutation bus

加入定交流电压附加控制后，故障期间，DC3系统逆变器通过调节功率因数，以阻止电压的深度跌落；故障清除后，换相电压恢复过程较平稳，电压波动较小，无后继换相失败，如图5（c）所示。DC2系统在加入附加控制后，扰动期间以母线电压为主要调节目标；随着系统恢复期间动态无功平衡问题得以解决，避免了由于强耦合作用引起的电压波动及后继换相失败，如图5（b）所示。同时DC1系统电压、电流暂态特性及熄弧角变化如图5（a）所示，在系统间的相互作用下，DC2、DC3系统换流母线电压稳定性提高对其也有一定的支撑作用，电压波动因此减小。综上可以看出，本控制方案能够改善联系较为紧密的多馈入系统电压稳定性，提高系统整体恢复速度。

5 结论

a.定交流电压附加控制配合定熄弧角控制，能够有效抑制定熄弧角控制的超调量带来的不利影响，提高电压扰动期间的稳定性，同时保证直流输电的经济运行。

b.电压稳定耦合因子指标能够表征某一直流换流母线电压受其余换流母线的影响的程度。以该指标来指导控制策略的布置方案能够反映出在哪些直流输电子系统中采用定交流电压控制取得的控制效果更好。

c.设计的平滑切换逻辑控制器，有效地减小了由于控制参数不同引起的切换振荡，保证系统工况改变时直流控制方式的顺利转换。

d.稳态降功率运行时，定最小熄弧角控制运行最经济，但是无功调节作用很小；定交流电压控制可调节的无功功率范围较大，能一定程度地减少无功设备容量。

［1］李兴源.高压直流输电系统［M］.北京：科学出版社，2010：120-122.

［2］汪娟娟，张尧，夏成军，等.交直流电力系统暂态电压稳定性综述［J］.电网技术，2008，32（12）：30-34.WANG Juanjuan，ZHANG Yao，XIA Chengjun，et al.Survey of studies on transient voltage stability of AC /DC power system［J］.Power System Technology，2008，32（12）：30-34.

［3］刘晓明，慈文斌，刘玉田.直流控制方式对受端电网电压稳定性影响［J］.电力自动化设备，2011，31（4）：69-77.LIU Xiaoming，CI Wenbin，LIU Yutian.Influence of DC system control mode on voltage stability of receiving-end power grid［J］.Electric Power Automation Equipment，2011，31（4）：69-77.

［4］张建设，张尧，张志朝，等.直流系统控制方式对大扰动后交直流混合系统电压和功率恢复的影响［J］.电网技术，2005，29（5）：20-24.ZHANG Jianshe，ZHANG Yao，ZHANG Zhichao，et al.Influence of DC system control modes on voltage and power recovery after large disturbance in hybrid AC /DC system［J］.Power System Technology，2005，29（5）：20-24.

［5］陈修宇，韩民晓，刘崇茹.直流控制方式对多馈入交直流系统电压相互作用的影响［J］.电力系统自动化，2012，36（2）：58-63.CHEN Xiuyu，HAN Minxiao，LIU Chongru.Impactofcontrol modes on voltage interaction between multi-infeed AC-DC system［J］.Automation of Electric Power Systems，2012，36（2）：58-63.

［6］郭利娜，刘天琪，李兴源.抑制多馈入直流输电系统后继换相失败措施研究［J］.电力自动化设备，2013，33（11）：95-99.GUO Lina，LIU Tianqi，LI Xingyuan.Measures inhibiting followup commutation failures in multi-infeed HVDC system［J］.Electric Power Automation Equipment，2013，33（11）：95-99.

［7］郑超，汤涌，马世英，等.直流参与稳定控制的典型场景及技术需求［J］.中国电机工程学报，2014，34（22）：3750-3759.ZHENG Chao，TANG Yong，MA Shiying，etal.A surveyon typical scenarios and technology needs for HVDC participated into stability control［J］.Proceedings of the CSEE，2014，34（22）：3750-3759.

［8］殷威扬，文俊，刘洪涛，等.葛—南直流输电工程无功及电压控制研究［J］.高电压技术，2006，32（9）：62-66.YIN Weiyang，WEN Jun，LIU Hongtao，et al.Research on the controlofreactivepower& AC voltagein Ge-NanHVDC transmission project［J］.High Voltage Engineering，2006，32（9）：62-66.

［9］郭小江，马世英，卜广全，等.上海多馈入直流系统的无功控制策略［J］.电网技术，2009，33（7）：30-35.GUO Xiaojiang，MA Shiying，BU Guangquan，etal.Reactive power control strategy for Shanghai multi-infeed DC system［J］.Power System Technology，2009，33（7）：30-35.

［10］杨卫东，徐政，韩祯祥.多馈入直流输电的协调恢复策略［J］.电力自动化设备，2002，22（11）：63-66.YANG Weidong，XU Zheng，HAN Zhenxiang.Coordinated recovery strategy for multi-infeed HVDC systems［J］.Electric Power Automation Equipment，2002，22（11）：63-66.

［11］HAMMAD A，SADEK K，KOELSH H，et al.Advanced scheme for AC voltage control at HVDC converter terminal［J］.IEEE Transactions on Power Apparatus and System，1985，PAS-104（4）：697-703.

［12］杨卫东，薛禹胜，荆勇，等.南方电网中多个直流系统间的协调功率恢复策略［J］.电力系统自动化，2003，27（15）：67-70.YANG Weidong，XUE Yusheng，JING Yong，et al.A coordinated recovery strategy for 3 HVDC systems involved ［J］.Automation of Electric Power Systems，2003，27（15）：67-70.

［13］浙江大学直流输电科研组.直流输电［M］.北京：水利水电出版社，1982：139-150.

［14］蔡泽祥，朱浩俊，白雪峰，等.多馈入直流输电系统的动态特性及稳定控制与分析［J］.华北电力大学学报，2004，31（5）：1-8.CAI Zexiang，ZHU Haojun，BAI Xuefeng，et al.Dynamic characteristics，stability controland analysis ofmulti-infeed HVDC transmission systems［J］.Journal of North China Electric Power University，2004，31（5）：1-8.

［15］欧开健，荆勇，任震.多馈入直流输电系统换流母线电压稳定性评估模型和算法［J］.电力自动化设备，2003，23（9）：23-26.OU Kaijian，JING Yong，REN Zhen.Model and algorithm for assessing voltage stability atcommutation buses in MIDC system［J］.Electric Power Automation Equipment，2003，23（9）：23-26.

［16］HAMMAD A，KUHN W.A computation algorithm for assessing voltage stability at AC /DC interconnections［J］.IEEE Transactions on Power Systems，1986，1（1）：209-215.

［17］金小明，周保荣，管霖，等.多馈入直流交互影响强度的评估指标［J］.电力系统自动化，2009，33（15）：98-102.JIN Xiaoming，ZHOU Baorong，GUAN Lin，et al.HVDC-interaction-strength index for the multi-infeed-HVDC power system［J］.Automation of Electric Power Systems，2009，33（15）：98-102.

［18］袁阳，卫志农，雷霄.多馈入直流输电系统换相失败研究综述［J］.电力自动化设备，2013，33（11）：140-147.YUAN Yang，WEI Zhinong，LEI Xiao.Survey of commutation failures in DC transmission systems［J］.Electric Power Automation Equipment，2013，33（11）：140-147.

［19］KUNDUR P.Power system stability and control［M］.New York，NY，USA：McGraw-Hill，1994：667-670.

［20］李佳，刘天琪，陈亮，等.基于理想点法的多准则综合灵敏度电压稳定评估指标［J］.电力自动化设备，2014，34（3）：108-112.LI Jia，LIU Tianqi，CHEN Liang，et al.Multi-criterion integratedsensitivity voltage stabilityevaluation indexbased on ideal point method［J］.Electric Power Automation Equipment，2014，34（3）：108-112.