基于多维度动态协调的大规模并网风电储能容量多指标优化配置策略

郭壮志，洪俊杰，孟安波

（广东工业大学 自动化学院，广东 广州 510006）

0 引言

在我国很多地区已形成由大规模并网风电和火电联合供电的局面。风电的时空分布不均衡、波动性和反调峰性，使得与火电在时空多维度上的动态协调能力不足，导致风电场的强迫弃风，不能充分发挥对火电的能源置换作用。随着储能技术的发展，其快速响应特征与功率能量的双向迁移能力，在改善风电出力波动性、提高风火电互补协调能力、优化能源利用效率等方面具有卓越优势［1］。但因受风能资源分布、负荷时空特征、火电运行特性限制等多重因素的影响，如何合理确定风电系统的储能配置容量已成为当前的研究趋势［2-13］。

目前，已有很多文献对含有风电的微电网系统［2］、配电网［4］、分布式系统［5］的储能容量配置策略开展研究，但其主要利用储能系统ESS（Energy Storage System）的双向快速功率迁移特性来平抑风电的短期功率波动，提高风电电源可靠性，增加储能系统生命使用周期，改善电能质量，提高系统稳定性等，对储能系统的时空多维度能量输移特性考虑不足，因此，难以将其直接应用于含大规模并网风电电力系统的储能容量配置［2-10］。

为降低大规模风电并网时的系统运行风险，提高风电电源的可靠性和可调度性等，国内外学者开始聚焦大规模并网风电的储能容量配置问题［11-15］。文献［11］考虑储能系统效率、荷电状态等制约，提出储能容量最小配置的离散傅里叶频谱分析方法，其可以较经济的成本投入显著降低风电的波动率，但该方法需通过反复的数值仿真计算，且未采用优化手段，确定的并非是容量最优值。文献［12］通过储能容量需求和负荷波动间的关系分析，提出以系统净负荷时间分布特性为主要考虑因素的优化配置方法，能够实现风电的接纳能力和系统运行综合收益间的协调。文献［13］以风电场出力特征分布函数和风速概率分布为基础，提出提高大型风电场功率长时间输出稳定性的储能容量配置方法。文献［14］考虑风功率和负荷双随机特性的储能功率配置方法，可得到风火储系统的备用系数、储能最小调节功率，提高对风电的接纳能力。文献［15］利用风电场中长期风速统计数据，提出最大化电池储能系统生命使用周期和提升风电场调度性的储能容量配置方法。

文献［11-15］主要从提高经济性、提升接纳水平及增强风电出力稳定性等方面，实现储能容量需求的协调配置，但其没有合理考虑风火储系统间的动态协调特性，所建模型难以有效反映风火储系统在时空多维度上的动态耦合关联关系及清洁风电时空尺度上的替代均衡作用，影响了风火储系统的经济高效运行。

本文针对大规模并网运行的风电场，假定各时段的预测功率分布已知且准确，以最大限度发挥风电对火电能源的替代置换为目的，研究考虑大规模风电与储能系统时空多维度上的动态耦合作用及风火储系统间的动态协调机制影响，兼顾储能系统功率调节与能量输移双重特征的容量多指标优化配置方法。

1 ESS对系统间动态协调机制的作用

1.1 风火电力系统协调机制分析的数学建模

图1为简化的风火储系统。与已有文献从经济性和风电间歇波动性角度分析不同，本文从能源时空多尺度利用角度，分析ESS对风火电力系统动态协调机制的影响规律。

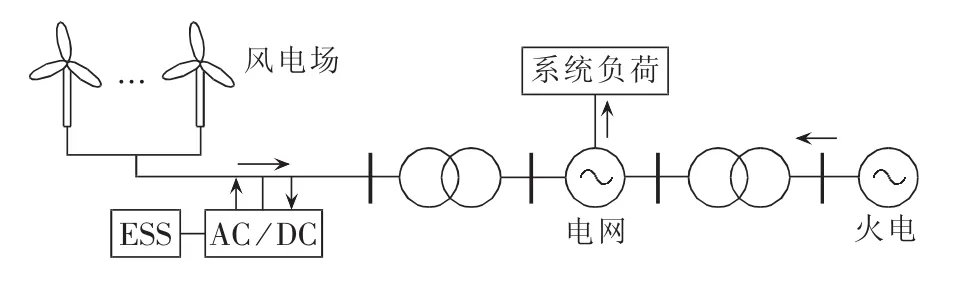
图1 简化的风火储电力系统Fig.1 Simplified WTE power system

风电出力间歇波动性和负荷随机性可视为系统净负荷预测偏差的动态分布对火电系统出力的再调整，故假定风电功率和系统负荷预测完全准确，ESS对风火电力系统的动态协调机制影响问题可描述为：已知调度期各时段风电预测功率和系统负荷，在满足系统负荷平衡、物理特性和运行约束下，ESS的功率能量输移特性对风电能源置换替代作用规律。

不考虑能量损失，仅从ESS功率能量的时空多维度迁移角度，分析其对调度周期内煤耗量的影响，数学模型可表示为：

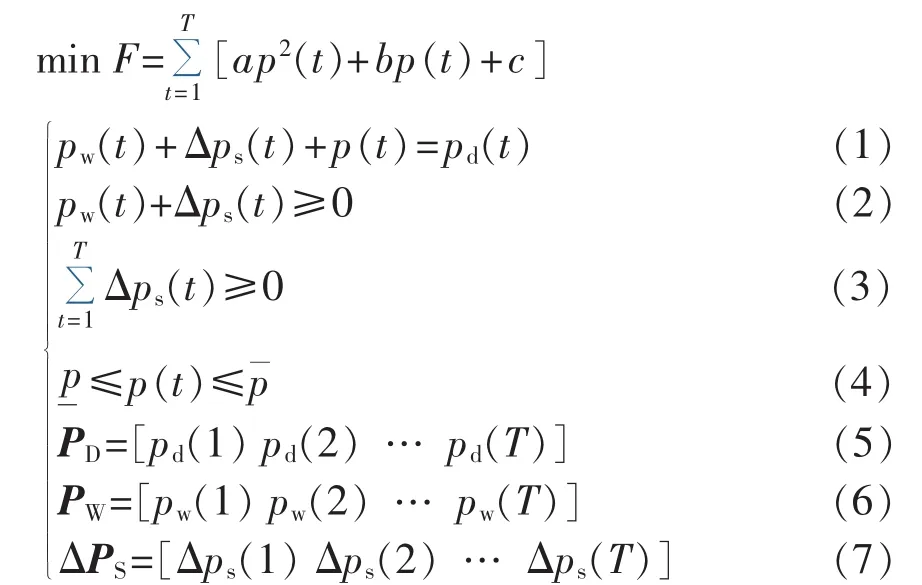
其中，PD、PW分别为调度期内系统负荷和等值并网风电场的预测功率向量；分别为火电厂出力 p的最小值和最大值；a、b、c分别为等值火电厂煤耗特性的一次系数、二次系数和常数项；ΔPS为ESS功率输移量；F为调度期内火电机组运行总煤耗量；T为调度总时段数。式（1）为考虑ESS影响的系统负荷平衡约束条件；式（2）、式（3）分别为风电场与 ESS 功率迁移和能量输移非负约束条件；式（4）为火电机组的出力约束条件。

依据上述模型，构造的拉格朗日函数为：

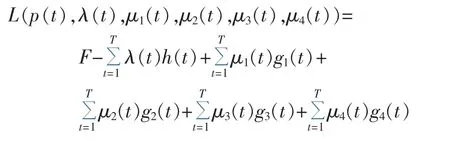
其中，λ（t）、μ1（t）、μ2（t）、μ3（t）、μ4（t）为拉格朗日乘子。

根据最优化理论［16］，可得到上述模型调度期内煤耗量最小的KKT极值条件为：

根据式（9）可知，储能功率迁移影响风电对火电的替代置换特征，以其为基础可分析ESS对动态协调机制的影响特性。

1.2 ESS对风火电力系统协调机制的影响分析

为简化分析，假设式（2）—（4）的约束条件都被满足，则式（9）的KKT条件可简化为：

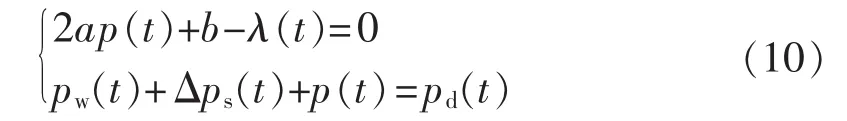
根据等微增率理论和式（10），可得到火电机组调度期内获得最小燃料耗量时 p（t）、pw（t）、Δps（t）、pd（t）间的量化关系为：

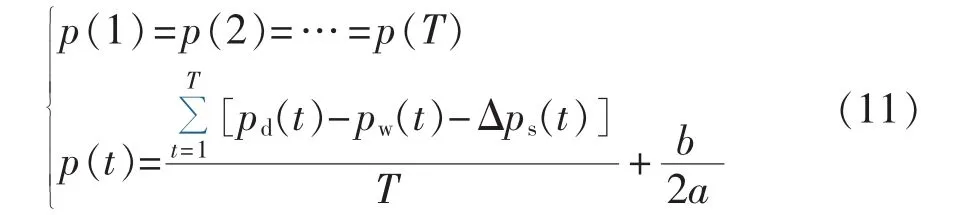
根据式（11）可知，各时段火电机组出力越小且相等时总燃料消耗量最小，因此，在满足各约束下，整个调度期内尽量保持火电机组承担负荷的出力均匀性。

当没有ESS时，为满足各时段火电机组出力均匀性，需利用风电对火电的协调机制动态调整其出力，但可能会增加弃风量，造成风电的替代置换效益降低。为增强风电的吸纳，减少清洁风电损失，火电需承担负荷调峰的任务，将使火电的煤耗量显著增加。

当火电、风电与ESS联合运行时，即Δps（t）存在，因ESS具有功率能量时空多维度的迁移能力，可根据ESS的电源与负荷双重效用动态协调风火电间的耦合特性，促使火电在尽量承担基荷的同时实现清洁风电的最大化利用。

1.3 大型并网风电场储能容量配置理论的可行性

以某简化风火电力系统为例分析ESS对风火电力系统协调机制的有效性。假定等值风电场电厂容量为300 MW，相邻时段预测功率为200、50 MW；火电机组容量为300 MW，煤耗特性系数a、b、c的值分别为 4.5×10-4t/（MW2·h）、0.3 t/（MW·h）、3.5 t/h；系统相邻时段预测负荷为300 MW、250 MW。

假定风电完全被系统消纳，表1为风火联合电力系统中储能容量配置对火电厂煤耗的影响。表中，PS为ESS配置容量；PT1、PT2分别为时段1、时段2机组出力；F1、F2、F分别为时段1、时段2和时段总煤耗量。

表1 储能容量配置对火电机组煤耗影响Table 1 Influence of ESS capacity on coal consumption of thermal unit

根据表1可以看出：当PS配置为0～50 MW时，随着ESS功率输移能力的增加，对火电机组出力进行调整能力的增强，虽导致时段1煤耗量增加，但因ESS的动态协调使时段2煤耗减少量大于时段1煤耗增加量，2个时段总煤耗降低，提升了风电能源的替代置换效益；当PS配置为50 MW时，可使时段1、时段2的机组出力相等，时段出力满足等微增率准则，系统时段总煤耗量最小，最大限度地发挥了风电的能源替代置换作用；当PS配置大于50 MW时，若储能容量全部用于功率输移，导致时段出力偏离等微增率点，使得时段2煤耗量的减少量小于时段1煤耗量的增加量，促使时段总煤耗量增加；PS配置为50 MW与没有配置储能相比，每小时可节约燃煤2.25 t，按月计算燃煤节约量将更加明显。虽然PS配置为50 MW时，系统时段煤耗量最少，但与PS配置为40 MW时相比，系统总煤耗仅节约了0.09 t。

根据以上分析可知：在大规模风火电协调运行电力系统中，合理配置ESS可充分发挥风电的能源互补优势，实现燃煤等非可再生能源的节约；储能容量配置并非越大越好，否则会增加系统运行成本，降低系统运行经济性；要从风电出力特征、系统负荷分布、火电运行特性、运行约束等方面综合确定大规模并网风电储能容量的配置。

2 风储系统动态耦合特性的数学描述

2.1 储能系统功率能量迁移特性

储能系统利用其对有功的存储和输出，实现有功能量在时空尺度分布上的动态调节，以满足电力能源的利用需求。考虑功率能量输移过程中的能源损失及能量的累积传递特性，其功率能量迁移的数学模型可表示为：

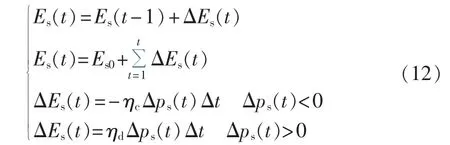
其中，Es0、Es（t）分别为时段初和 t时段 ESS 存储的电能；ΔEs（t）为 t时段 ESS 能量变化量；ηc、ηd分别为ESS的充、放电效率；Δt为单一时段的时间间隔。

2.2 风储系统的动态耦合特性

风储系统的动态耦合特性反映储能系统功率能量的输移对风电功率净输出特性的调节，其数学模型可表示为：

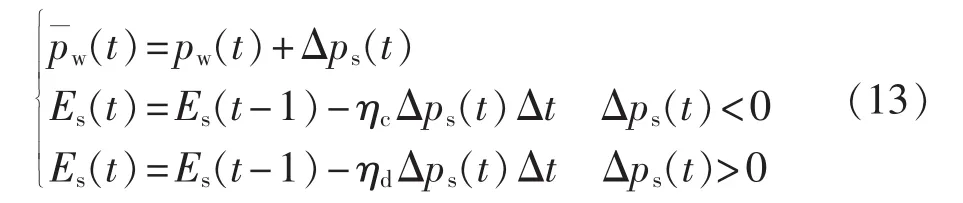
其中为风电输出的净功率。

3 风火储系统储能容量的多指标配置模型

3.1 容量配置模型的多效益指标

目前，大部分储能容量配置模型是在满足各种物理、运行、系统等约束下的调节功率或经济成本等单一指标的最优［17-19］。而实际上受资源制约、成本影响、节能要求、运行特性限制等因素的影响，储能容量优化配置本质上是多个指标间的协调问题。本文从ESS的多维度动态互济特征和火电机组节能运行角度构建多效益指标的储能容量优化配置模型。

（1）调度期内煤耗量最小指标。

在大规模风火储电力系统中，为促进非可再生能源的可持续高效利用，进行储能容量配置时，除考虑提高风电吸纳水平和利用效率外，其中一个主要目标就是需在满足电力供需平衡的前提下，充分利用ESS的功率能量时空多维度动态耦合输移特性，增强风电的置换互补效益，最大限度地降低燃煤等非可再生能源的使用量，即整个调度期内煤耗量最小。优化指标可表示为：

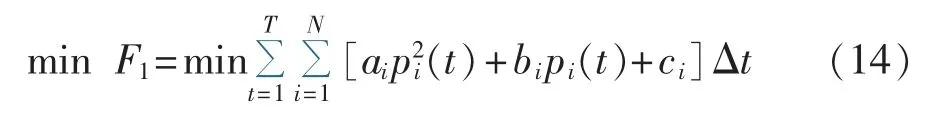
其中，ai、bi、ci分别为机组 i煤耗特性的一次系数、二次系数和常数项；pi（t）为机组i时段 t的出力；N 为火电机组数。

（2）储能功率与能量综合协调最小指标。

针对大规模风电的储能容量配置，要同时兼顾ESS功率调节和动态能量输移特性。储能容量越大其功率能量输移特性越强，但其成本也越高［15］。因此，进行容量配置时，期望以较小的功率调节容量和能量输移容量最大化风储系统时空多维度上的耦合互济能力，提高风电接纳水平和增强其能源替代置换效益。考虑储能功率与能量综合协调时的优化指标为：

其中，t=1，2，…，T。

式（15）优化指标的物理含义是在有效实现功率调节容量和能量输移容量间动态协调的前提下，以较小的技术代价最大化ESS的多维度动态协调能力。

3.2 容量配置优化模型相关约束

在风火储电力系统中，容量配置优化模型约束条件包括风电相关约束、火电相关约束、储能系统特性约束、系统约束、备用约束，此外还有动态协调约束、能量守恒约束、能量循环约束等。

（1）火电机组出力约束。

火电机组运行时，因其机组容量和运行特性限制，其功率输出应满足最大最小出力范围，可表示为：

其中分别为火电机组i的最大、最小出力。

（2）火电机组爬坡约束。

火电机组单位时间内允许的最大功率调节量因受物理运行特性限制是有限值。其上行和下行爬坡速率约束的数学模型可表示为：

其中分别为每分钟火电机组i允许的最大出力上行和下行的功率变化量。

（3）火电机组综合最小出力约束。

受物理特性、系统运行安全可靠性、能源利用要求等因素的影响，要求火电机组综合出力满足最小出力运行要求。其约束条件可表示为：

其中，为最小火电机组群出力。

（4）风电场出力约束。

受火电运行特性、系统运行方式、负荷分布特征、ESS耦合协调机制等因素影响，假定风电场时段预测功率准确无误差，其承担系统负荷的最大功率输出为功率预测值。其数学模型可表示为：

其中分别为风电场t时段预测功率和允许的最小输出功率。

（5）风电与ESS间耦合协调约束。

当ESS向电网供电时，为充分发挥风电的能源替代置换效益，风电场要按照预测功率承担负荷。其约束条件可表示为：

（6）风电与ESS间功率转移守恒约束。

当风电功率迁移到ESS时，考虑运行时可能产生弃风情况，依据能量守恒，风电场承担负荷与转移功率之和应不大于风电预测功率。其约束条件为：

（7）风电与ESS耦合功率输出约束。

依据能量守恒特性和风储系统功率能量迁移特性，风电与ESS在调度时段的功率输出应为非负值，其耦合功率输出约束可表示为：

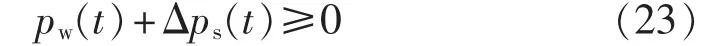
（8）ESS能量转移耦合约束。

根据式（12），储能系统能量转移耦合约束为：

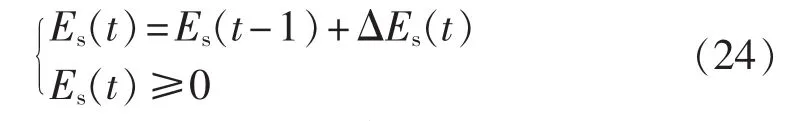
（9）ESS能量耦合传递约束。

根据式（12），储能系统能量耦合传递约束为：

（10）ESS周期能量循环约束。

为促进储能配置容量的最充分利用和风电能源的高效利用，ESS能量存储应保证周期循环性，即初末能量相同，其约束条件数学模型可表示为：

（11）ESS功率能量输移协调约束。

利用ESS进行风电功率能量输移过程中，由于能量损失导致风电转移功率能量和ESS实际功率能量存储存在差异，其约束条件的数学模型可表示为：

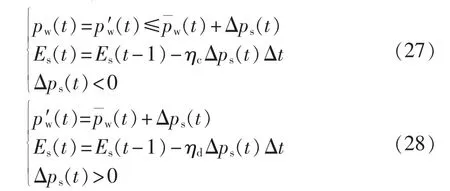
（12）风储系统耦合功率输出波动指标约束。

为降低风电波动性，提高风电吸纳水平，提升风电并网运行时的系统稳定性，在整个调度期内期望风电与ESS协调输出功率最小值和最大值的比值满足给定的水平。其约束条件数学模型可表示为：

其中，Er为给定的最大波动指标。

（13）风火储系统负荷平衡松弛约束。

考虑到处于储能容量规划阶段，在每个调度时段，只需要保证系统综合出力不小于系统负荷，负荷平衡松弛约束条件的数学模型可表示为：

（14）火电旋转备用约束。

火电旋转备用约束可表示为：

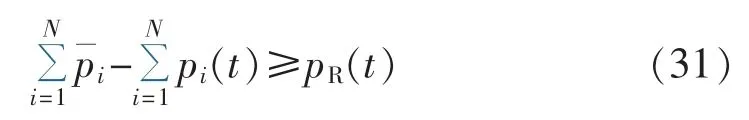
其中，pR（t）为t时段火电厂最小的备用容量。

3.3 容量优化配置多指标模型理论分析

根据3.1节所构建的储能容量配置模型中相关的优化指标和约束条件可知：

a.建立的容量配置多指标模型，其物理意义为以最小的储能功率能量调节容量，实现风电的最大化利用和燃煤等非可再生能源最大限度的节约，体现多尺度上系统运行经济性和技术性间的动态协调；

b.所构建的约束条件不仅考虑了风火储系统间功率耦合协调机制，且有效考虑了储能系统的能量输移特性，融合了1.1节中分析的储能系统时空多维度上的能量迁移特性，有利于优化时空多尺度上风火储系统间的动态协调机制，增强风电吸纳能力和风电对火电的置换作用，促进能源可持续高效利用。

4 容量配置多指标模型求解

由于储能功率与能量综合协调指标的存在，模型具有强的非线性特点；因储能系统功率能量输移协调约束可能存在间断不连续特征，导致模型求导运算比较复杂；风储系统耦合功率输出波动指标、储能系统能量输移守恒约束、系统间耦合协调约束以及变量间的关联耦合特性等，使得利用以梯度为基础的优化算法进行求解时比较繁琐，因此，采用无需梯度的群体智能全局搜索算法进行求解。

在模型中，所有的变量都可以采用 pw（t）、pi（t）和 Δps（t）进行表示，因此，以 pw（t）、pi（t）和 Δps（t）为内生变量。多指标模型可以表示为：

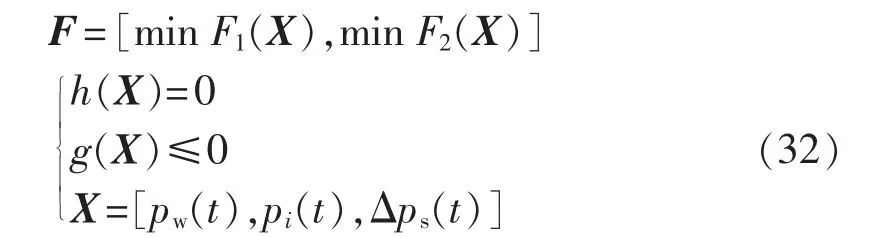
本文主要分析各优化指标对储能容量配置大小的影响规律，因此，对优化指标的处理采用权重法；对于等式约束和不等式约束采用罚函数法。采用群体智能算法求解的评价函数可表示为：

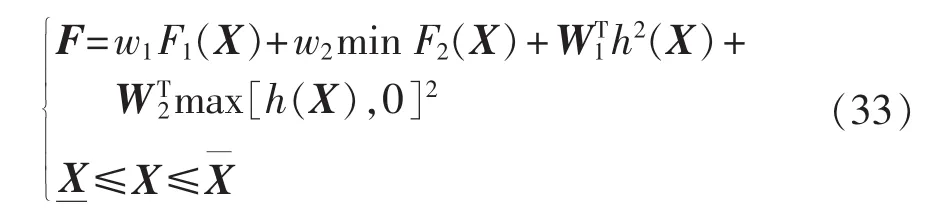
其中分别为内生变量的最小值和最大值；w1、w2为优化指标的权重系数；为罚系数。

风储系统耦合功率输出波动指标为分式约束条件，max［pw（t）+Δps（t）］的值始终大于零，为避免分式约束条件的存在使计算变得复杂，可将式（29）变换为式（34），然后利用罚函数法将其融入式（33）中。

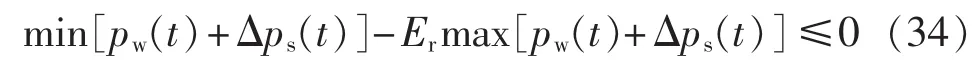
利用群体智能算法进行求解的基本步骤如下。

a.确定权重系数w1与w2、罚系数W1T与W2T的值；初始化种群个数、内生变量上下限及算法的初始化参数和算法终止条件。

b.以 pw（t）、pi（t）、Δps（t）作为决策变量产生初始种群，并利用群体智能算法的搜索策略产生新的种群 Xk和 X′k。

c.利用适应度函数计算Xk和X′k对应的函数值F（Xk）与 F（X′k），当 F（Xk）≤F（X′k）时，将 X′k中的个体代替Xk中的个体作为新的Xk。

d.判断算法是否满足终止条件，若不满足则继续步骤b、c，若满足则输出最终目标函数值和对应ESS的配置容量值。

5 算例分析

5.1 算例描述

采用含1个大型并网风电场和5台火电机组的风火储系统为例分析。风电数据来源于我国某实际大型并网风电场，含433台风机，单台额定出力为1.5MW。图2为风电场一天的风电预测出力；图3为依据实际数据适当改造得到的负荷分布；表2为根据实际数据拟合得到的火电机组煤耗特性系数；ESS充放电效率为90%。以15 min为间隔，考虑1 d为周期，利用MATLAB7.0遗传算法工具箱验证并网风电储能容量多维度动态协调配置策略的有效性。

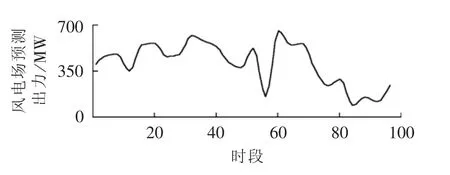
图2 风电场预测出力值Fig.2 Forecasted power output of wind farm

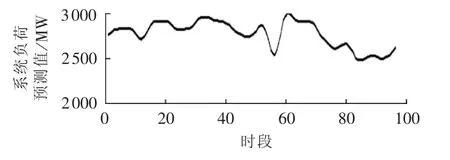
图3 风火储系统负荷Fig.3 Load of WTE system

表2 火电机组参数Table 2 Parameters of thermal units

5.2 储能配置策略有效性

本文采用权重系数法将煤耗量和综合协调指标转化为单目标，通过权重系数调整分析优化指标对储能配置容量和系统煤耗量的影响规律。单指标模型为：

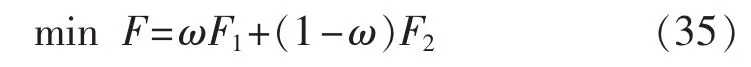
其中，ω为权重系数。

图4为ESS功率动态多维度协调规律；图5为ESS能量动态协调规律。

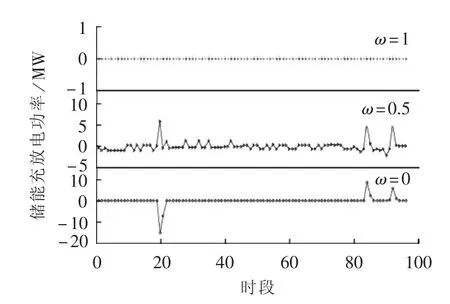
图4 ESS功率动态协调规律Fig.4 Dynamic power coordination law of ESS

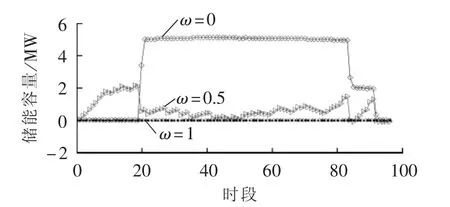
图5 ESS能量动态协调规律Fig.5 Dynamic energy coordination law of ESS

表3所示为ω取值0、0.5和1时大规模风火储系统储能容量优化配置结果。表中，CV为约束条件最大违背值；CP为拉格朗日条件取值。由表3可见，3种情况下CV、CP的值约为0，表明结果满足拉格朗日极值和约束条件。

当ω=1时，优化模型中仅存在储能功率与能量综合协调最小指标，风电场在满足系统约束下，按照预测出力承担负荷；根据图4和表3可知，系统功率容量配置最小，功率配置为0MW，容量配置为0MW·h，系统煤耗量最大，为12902 t。

当ω=0时，优化模型中仅存在煤耗量最小指标。根据图4，为发挥风电替代置换作用，其储能功率容量配置最大，在满足功率能量转移守恒、能量非负等约束条件下，通过ESS的多时空迁移特性实现对风电场功率能量的迁移，最大限度地提高风电对火电的替代置换效益；依据表3可知，功率配置为15MW，容量配置为5.1 MW·h，系统一天的煤耗量为12884.4 t。

当ω=0.5时，优化模型中同时存在储能功率与能量综合协调最小指标和煤耗量最小指标。根据图4，其储能功率和容量的配置值，大于ω=0并小于ω=1时的配置值；根据表3，系统煤耗量处于ω=0、ω=1这2种情况之间时，为12886.5 t。

依据上述分析可知：所构建ESS多指标优化配置模型，在充分考虑其功率能量迁移特性和系统运行综合经济性时，根据系统要求、决策者偏好等，可从功率、能量双重角度实现储能功率容量的协调配置。

表3 储能容量配置结果Table 3 Results of energy storage capacity configuration

5.3 储能容量配置对火电厂运行的影响分析

表4为ω=0、ω=0.5、ω=1这3种不同储能容量配置下火电厂运行优化结果。表中，ΔF1为ω=1与ω=0时火电厂煤耗量增量；ΔF2为ω=1与ω=0.5时火电厂煤耗量增量。本文从ESS不同容量配置下，分析其功率传递与能量时空多维度输移特性对火电厂节能运行的影响。

ω=1，即没有储能容量配置时，火电厂承担系统总负荷最小，为41 274 MW，但其煤耗量最大，为12 902 t。根据1.1—1.3节理论可知，虽然此时风电承担的负荷最大，受风电出力特性在时间分布上的不均衡性影响，在满足电力供需平衡和约束下，火电厂各时段出力因偏离最佳协调点较远，导致煤耗量反而增加。

ω=0，即储能容量配置为15 MW时，火电厂承担系统总负荷大于ω=1时的负荷，为41280.6 MW，但其煤耗量最小，为12884.4 t。根据1.1—1.3节理论可知，虽然此时因为在迁移过程中能量损失而导致风电承担的负荷降低，但同时储能系统对风电功率能量的迁移作用，使得在满足电力供需平衡和约束下，火电厂各时段出力更加接近最佳协调点，此时所节约的煤耗量大于风电损失所替代的煤耗量，因此火电厂煤耗量减少。

ω=0.5与ω=0时相比，因储能容量配置降低，导致储能系统时空多维度上的功率能量迁移能力降低，从而削弱了其对风电时空分布特性的影响，使得火电厂出力远离最佳协调点，因此，火电厂煤耗量增加，为12 886 t，但其容量配置比ω=0时减少了9.3 MW。

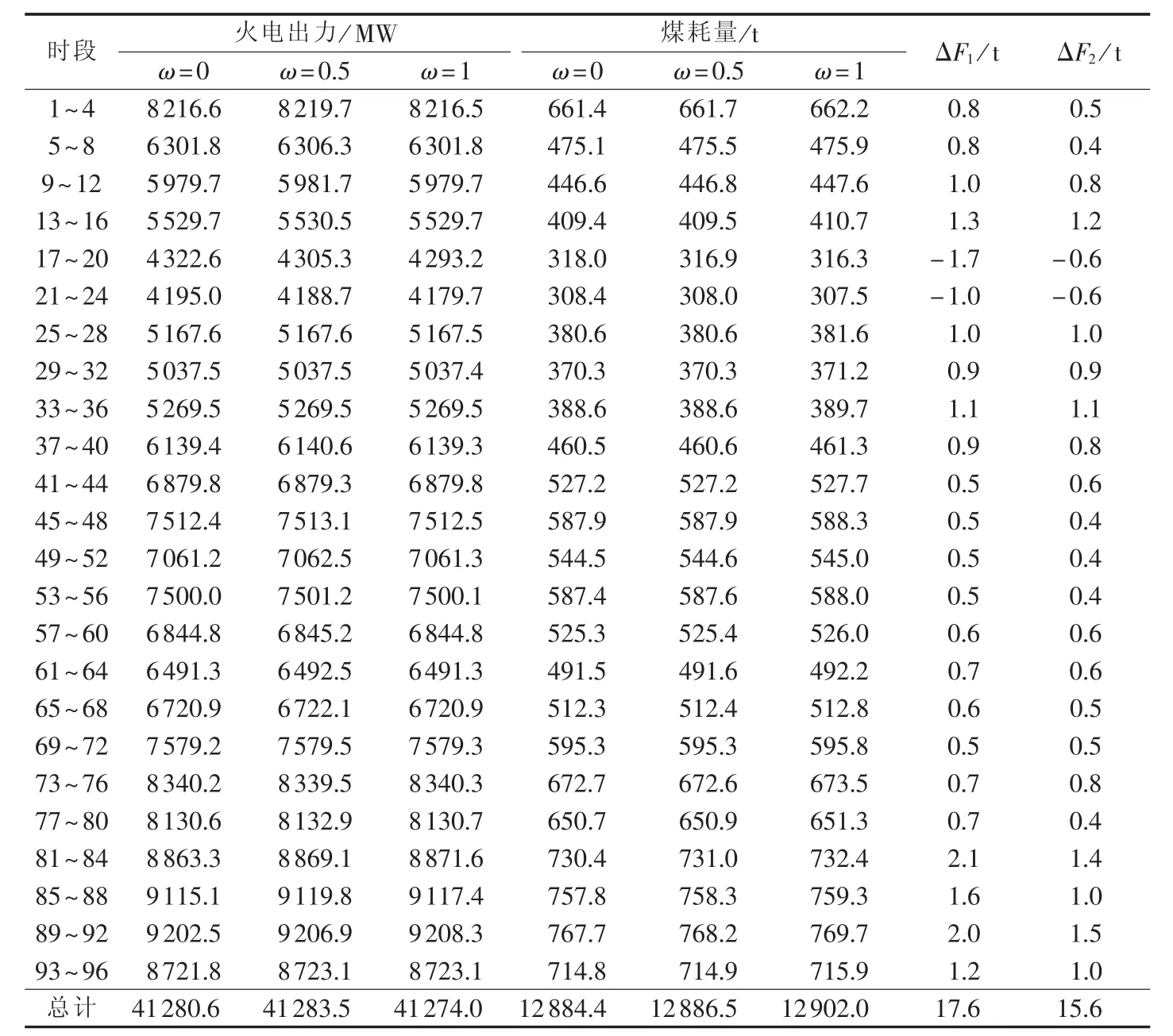
表4 火电厂优化运行结果Table 4 Results of thermal plant optimal operation

由上述分析可知：通过ESS容量的合理配置，利用其在时空多维度上的功率能量迁移特性优化火电厂的净负荷特征，可改善火电厂出力特性，实现节能降耗的目的；当ESS容量配置达到一定规模时，其功率能量迁移所产生的作用将会明显降低，因此，其容量配置并非越大越好，要从综合指标的角度协调。

6 结论

a.利用ESS功率能量迁移特性提高大规模并网风电的替代置换效益理论上是可行的，通过从功率能量双重角度实现储能容量的合理协调配置，可明显降低火电厂的燃料消耗量，提高系统运行的综合经济性。

b.本文提出的风火储时空多维度动态协调理论是正确有效的，以此为基础所构建的大规模风火储电力系统储能容量多指标配置新模型，不仅可实现调节容量和风电功率输出特性间的协调，且可根据系统综合运行要求，有效反映风火储系统时空多尺度上的动态互济特征，实现对储能功率和容量双重指标综合配置，提高风电在时空多维度上的能源替代置换作用。

［1］陈谦，陈霄逸，金宇清，等.基于混合储能的大型风电场优化控制［J］.电力自动化设备，2015，35（4）：70-76.CHEN Qian，CHEN Xiaoyi，JIN Yuqing，et al.Optimal control of large-scale wind farm based on hybrid energy storge［J］.Electric Power Automation Equipment，2015，35（4）：70-76.

［2］BAHRAMIRAD S，REDER W，KHODAEIA.Reliabilityconstrained optimal sizing of energy storage system in a microgrid［J］.IEEE Transactions on Smart Grid，2012，3（4）：2056-2062.

［3］张熙，张峰，巩乃奇，等.基于荷电状态动态调整的储能电站容量规划［J］.电力自动化设备，2015，35（11）：20-25.ZHANG Xi，ZHANG Feng，GONG Naiqi，et al.BESS capacity planning based on dynamic SOC adjustment［J］.Electric Power Automation Equipment，2015，35（11）：20-25.

［4］林少伯，韩民晓，赵国鹏，等.基于随机预测误差的分布式光伏配网储能系统容量配置方法［J］.中国电机工程学报，2013，33（4）：25-33.LIN Shaobo，HAN Minxiao，ZHAO Guopeng，et al.Capacity allocation of energy storage in distributed photovoltaic power system based on stochastic prediction error［J］.Proceedings of the CSEE，2013，33（4）：25-33.

［5］吴红斌，郭彩云.计及电动汽车的分布式发电系统中储能单元的优化配置［J］.中国电机工程学报，2012，32（增刊）：15-21.WU Hongbin，GUO Caiyun.Capacity optimization of energy storage unit in distribution generation system considering electric vehicle［J］.Proceedings of the CSEE，2012，32（Supplement）：15-21.

［6］吴云亮，孙元章，徐箭，等.基于饱和控制理论的储能装置容量配置方法［J］.中国电机工程学报，2011，31（22）：32-39.WU Yunliang，SUN Yuanzhang，XU Jian，et al.Determination methodology for energy storage capacity based on saturation control theory［J］.Proceedings of the CSEE，2011，31（22）：32-39.

［7］韩晓娟，程成，籍天明，等.计及电池使用寿命的混合储能系统容量优化模型［J］.中国电机工程学报，2013，33（34）：91-97.HAN Xiaojuan，CHENG Cheng，JI Tianming，et al.Capacity optimal modeling of hybrid energy storage systems considering battery life［J］.Proceedings of the CSEE，2013，33（34）：91-97.

［8］刘春燕，晁勤，魏丽丽.基于实证数据和模糊控制的多时间尺度风储耦合实时滚动平抑波动［J］.电力自动化设备，2015，35（2）：35-41.LIU Chunyan，CHAO Qin，WEI Lili.Wind-storage coupling based on actual data and fuzzy control in multiple time scales for realtime rolling smoothing of fluctuation［J］.Electric Power Automation Equipment，2015，35（2）：35-41.

［9］SHI J，TANG Y，DAI T，et al.Determination of SMES capacity to enhance the dynamic stability of power system ［J］.Physica C：Superconductivity，2010，470（20）：1707-1710.

［10］MOHOD S W，HATWAR S M，AWARE M V.Grid support with variable speed wind energy system and battery storage for power quality［J］.Energy Procedia，2011，12（1）：1032-1041.

［11］王成山，于波，肖峻，等.平滑可再生能源发电系统输出波动的储能系统容量优化方法［J］.中国电机工程学报，2012，32（16）：1-8.WANG Chengshan，YU Bo，XIAO Jun，et al.Sizing of energy storage systems for output smoothing of renewable energy systems［J］.Proceedings of the CSEE，2012，32（16）：1-8.

［12］严干贵，冯晓东，李军徽，等.用于松弛调峰瓶颈的储能系统容量配置方法［J］.中国电机工程学报，2012，32（28）：27-35.YAN Gangui，FENG Xiaodong，LI Junhui，et al.Optimization of energy storage system capacity for relaxing peak load regulation bottlenecks［J］.Proceedings of the CSEE，2012，32（28）：27-35.

［13］韩涛，卢继平，乔梁，等.大型并网风电场储能容量优化方案［J］.电网技术，2010，34（1）：169-173.HAN Tao，LU Jiping，QIAO Liang，et al.Optimized scheme of energy-storage capacity for grid-connected large-scale wind farm［J］.Power System Technology，2010，34（1）：169-173.

［14］黎静华，文劲宇，程时杰，等.基于p-有效点理论的含大规模风电电力系统最小储能功率配置方法［J］.中国电机工程学报，2013，33（13）：45-52.LI Jinghua，WEN Jinyu，CHENG Shijie，et al.Method of minimum energy storage power allocation for electric power systems with large-scale wind power based on p-efficient point theory［J］.Proceedings of the CSEE，2013，33（13）：45-52.

［15］LI Q，CHOI S S，YUAN Y，et al.On the determination of battery energy storage capacity and short-term power dispatch of a wind farm［J］.IEEE Transactions on Sustainable Energy，2011，2（2）：148-158.

［16］张立卫.最优化方法［M］.北京：科学出版社，2010：150-155.

［17］徐林，阮新波，张步涵，等.风光蓄互补发电系统容量的改进优化配置方法［J］.中国电机工程学报，2012，32（25）：88-98.XU Lin，RUAN Xinbo，ZHANG Buhan，et al.An improved optimal sizing method for wind-solar-battery hybrid power system［J］.Proceedings of the CSEE，2012，32（25）：88-98.

［18］CHEN S X，GOOI H B，WANG M Q.Sizing of energy storage for micro-grids［J］.IEEE Transactions on Smart Grid，2012，3（1）：142-151.

［19］马溪原，吴耀文，方华亮，等.采用改进细菌觅食算法的风/光/储混合微电网电源优化配置［J］.中国电机工程学报，2011，31（25）：17-25.MA Xiyuan，WU Yaowen，FANG Hualiang，et al.Optimal sizing of hybrid solar-wind distributed generation in an islanded microgrid using improved bacterial foraging algorithm ［J］.Proceedings of the CSEE，2011，31（25）：17-25.