暂态稳定视角下的最佳重合闸时间及其在线整定
王羽佳,李华强,黄 燕,凡 航
(四川大学 电气信息学院,四川 成都 610065)
0 引言
自动重合闸已广泛用于高压输电线路,大幅提高了输电线路运行可靠性以及电力系统并列运行的稳定性[1]。工程实际中自动重合闸未考虑故障类型,采用经固定延时后重合的简单逻辑,然而最佳重合闸时间随着故障类型不同而不同,此时可按照最严重故障情况(即发生永久性故障)来整定重合闸时间,以避免盲目重合于永久性故障时系统遭受严重冲击[2-4]。随着自适应重合闸研究的发展,能够通过区分瞬时性故障和永久性故障判断是否重合闸,但是难以判定故障类型的情况时有发生[5],为尽量满足供电可靠性与连续性,此时重合闸必须顾及当系统发生最坏情况时的重合闸后果。为将重合不成功对系统的冲击降低至最小,重合闸时间应满足永久性故障的最佳重合条件[6-7]。 已有研究[2,8-9]表明,对于永久 性故障,重合于最佳时间能使得断路器再次跳开后系统暂态能量显著减小,有利于提高系统暂态稳定性,若能在线整定出最佳重合闸时间,以最小冲击的方式重合,将极大程度地化不利为有利。故永久性故障最佳重合闸时间的在线整定研究具有较大的工程意义和理论价值。
文献[10-11]通过对重合闸条件机理的分析,分别用发电机功角与相对角速度推导出瞬时性故障与永久性故障的最佳重合闸条件。文献[12]考虑到系统暂态失稳通常呈现出双机失稳模式,选择用扩展等面积准则 EEAC(Extended Equal Area Criterion)等值法判断永久性故障的最佳重合闸时间,其本质是运用暂态能量函数方法寻找最佳重合闸时间,但因其计算复杂,并且需要考虑发电机全局信息,难以满足电力系统运行条件实时变化的需求,并不适合工程实际中重合闸时间的在线整定。文献[13]详细分析了暂态能量在电力系统中的分布变化,将关注点从发电机信息转移到输电网络暂态能量分布上,提出了用局部观测信息实时判断永久性故障最佳重合闸时间的方法。文献[3-4]提出依赖发电机总动能确定永久性故障最佳重合闸时间的方法,然而其未对重合闸机理进行详细分析证明,并且未考虑系统双机失稳模式,有所欠缺。
本文认为,最佳重合闸时间在线整定方法要能应对系统复杂多变的运行情况,需要进行以下两方面的工作:一是对最佳重合闸条件判据进行一定程度的简化,力求判据不仅限于发电机内部信息,可利用诸如广域测量系统(WAMS)量测的实时量测数据等信息;二是根据实测信息在线准确预测出最佳重合闸时间。
本文以转子角速度为切入点,对单机无穷大系统永久性故障的最佳重合闸条件进行分析,得到发电机转子角速度最小能近似等效永久性故障最佳重合闸条件的结论,继而在多机系统推广应用中,基于双机等值思想推导出整定最佳重合闸时间的绝对动能判据,并构建稳定指标反映重合后系统的稳定程度。同时由WAMS实时采集的少量数据,对故障后发电机等值角速度采用曲线特征拟合法进行在线预测,给出一种最佳重合闸时间的在线整定方法。仿真结果表明,该方法能在线预测出最佳重合闸时间,有效阻尼系统摇摆,提高系统暂态稳定性,所需数据量小,误差小。
1 最佳重合闸机理分析
工程实际中或者故障类型难以判定时,为极大发挥重合闸作用,重合闸时间可按永久性故障来整定,若重合时间选择正确,会使初次故障产生的能量与重合闸操作产生的能量相互抵消,达到提高系统暂态稳定性的目的。传统分析认为永久性故障最佳重合闸条件为发电机的功角由最大开始减小时和相对角速度Δω达到负的最大值之前[11]。故对最佳重合闸条件的研究普遍由综合考虑功角和相对角速度的暂态能量函数法得出。然而该方法存在以下不足:传统的最佳重合闸条件综合考虑功角与相对角速度,使得这一条件很难在线整定得出;在相对动能的形式下,减速机组可能会出现动能增加这一不合理的现象[14],不利于观测机组减速过程;功角(或暂态势能)与永久性故障的最佳重合闸条件缺乏必然联系。
鉴于上述不足,考虑到发电机转子角速度响应可以反映系统在任何大扰动下发电机的运行状态,本文从转子角速度分析出发,对永久性故障最佳重合闸条件进行简化。以单机无穷大系统线路发生永久性故障前后的功角特性曲线为例进行分析。图1为永久性故障前后的功角特性曲线。
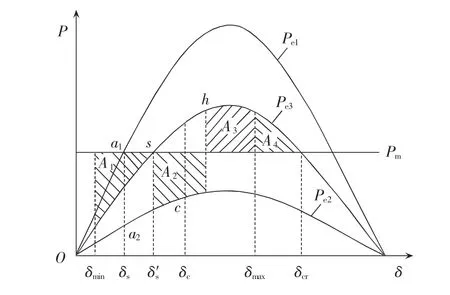
图1 功角特性曲线Fig.1 Curves of power-angle characteristic
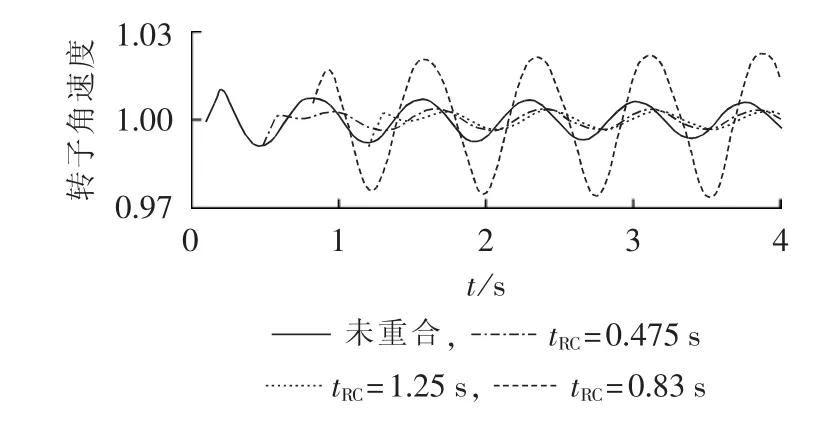
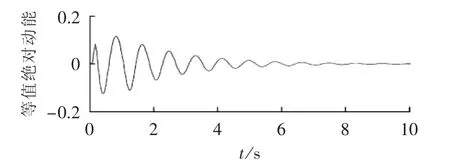
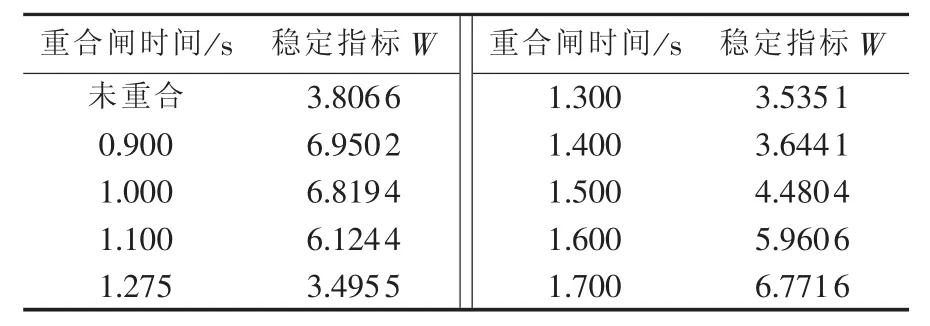
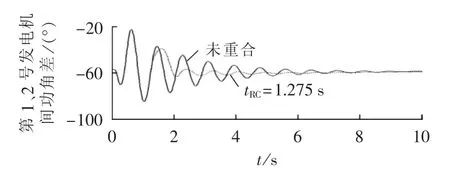
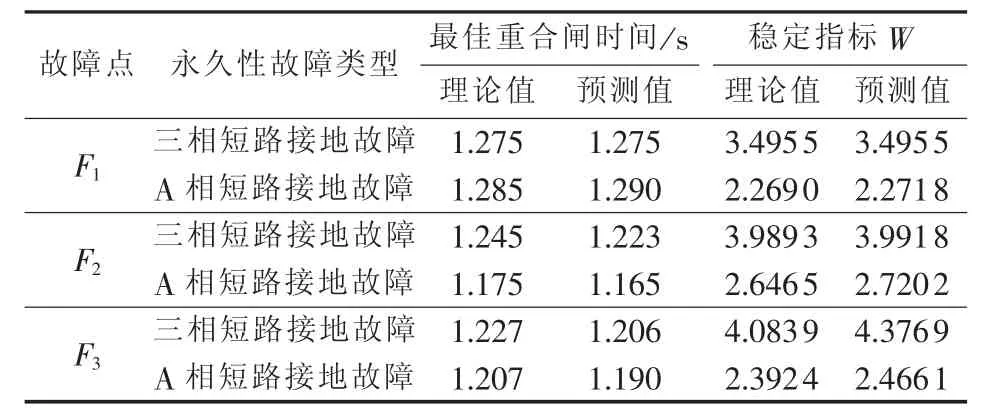
系统正常运行在功角特性曲线Pe1的a1点,与此对应的功角为δs,角速度为ωN。故障瞬间,运行点将突降至故障时的功角特性曲线Pe2的a2点。c点故障切除,此后的重合闸间歇时间里,由等面积定则可知发电机转子角速度在(ωN、ωmin、ωmax分别为额定转子角速度、最小转子角速度和最大转子角速度)之间变化。重合于永久性故障对系统而言总是注入动能,产生加速力矩;若在第二摆的振荡过程中,机组加速接近于新的稳定平衡点s(此时角速度为ωmax)处重合闸,因为重合于永久性故障,将继续为系统注入动能,使得角速度继续增加。经过一定时间故障切除,若减速能量不能平衡之前累积的加速能量(即A3+A4 为了阻尼后续摆的摇摆程度,重合闸动作必然应选在故障切除后机组的减速时刻。若在机组减速过程中,这一摆中剩余的减速能量能够平衡重合于故障产生的加速能量,并且希望故障再次切除后,系统运行点能稳定过渡到新的稳定平衡点,那么对应的重合闸时刻即为最佳重合闸时间(若A2=A3,则此点可认为是回摆过程中的h点)对应的时刻。然而这一时刻很难在线精准定位,故需寻求一个近似等效时刻。考虑到发电机角速度达到极小值时重合于永久性故障,能最大限度吸纳重合闸所注入的动能,故本文认为在工程实际中,此时刻可等效为最佳重合闸时间。 在难以判别故障类型时,若实为瞬时性故障,按照永久性故障整定出的最佳重合闸时间(即ωmin时刻)避开了瞬时性故障的最差重合时间(Δω=0且δ=δmax的时刻),重合后只影响系统的振荡幅度,对暂态稳定性影响不大。故在无法判定故障类型时,按照永久性故障情况来整定重合闸时间是合理可行的。 单机系统中,由发电机转子角速度最小可直接推导出永久性故障的最佳重合闸时间,然而对于多机系统,故障发生时,送端机组由于失去部分负荷,机械转矩将大于电磁转矩,导致角速度增长,受端机组反之亦然,故不同发电机将会呈现不同的转子角速度特性。基于上述考虑,本文提出以等值系统下的绝对动能判据寻找最佳重合闸时间。 作用于发电机转子上的不平衡功率对时间进行积分反映的是转子绝对动能增量[14]。与此同时,考虑到对于功角稳定而言,系统总表现在2个机群间失去同步。为着重体现导致系统失步的2个机群间的相对运动,本文参考绝对动能的概念,基于双机等值思想,推导出等值系统中绝对动能的表达形式。 对于计算最佳重合闸时间的双机等值方法,只需反映实际故障切除时系统的简单分群情况即可[12]。本文所使用的分群方法是计算故障发生时刻,各发电机的加速功率和惯性时间常数之比Pace,i/TJi,以此排队,筛选出临界机组[15]。设临界机组即严重受扰的机群为S群,它有1个惯量中心,而其余机组为A群,也有其惯量中心,定义2个惯量中心的等值角速度、功角和等值惯性时间常数分别为: 其中,ωi、δi、TJi和 ωj、δj、TJj分别为第 i号和第 j号发电机的角速度、功角和惯性时间常数。 双机等值时,系统惯量中心S、A的运动方程为: 其中,Pmi、Pei和 Pmj、Pej分别为第 i号和第 j号发电机的机械功率和电磁功率。 进一步得出等值单机无穷大系统运动方程为: 则等值系统中绝对动能增量的表达式为: 对应的转子绝对动能WV的标幺值表达式为TJeqωeq,即: 可见只需要计算系统的等值惯性时间常数和等值角速度,即可求得等值系统的转子绝对动能。转子绝对动能最小的时刻,即为多机系统发生永久性故障的最佳重合闸时间。此外,整定最佳重合闸时间应考虑系统是否暂态失稳这一条件。若故障切除后,系统中最大功角差超过一定阈值判定系统失稳,此时重合闸装置闭锁。 为了评估重合闸对系统暂态稳定的影响程度,本文定义稳定指标W: 其中,T为仿真时间;i与n分别为发电机编号与发电机总台数。 W是作用在发电机上不平衡功率的绝对值对时间的积分。该指标直观体现了发电机机械功率和电磁功率相互抵消的累积程度,间接反映系统转子角速度振荡的严重程度以及发电机动能变化趋势的绝对值,能评估重合闸操作对系统暂态稳定的影响。W越小,系统越稳定。 值得一提的是,最佳重合闸时间的整定需考虑重合闸间歇时间因素。根据我国电力系统行业的运行经验,重合闸最小间歇时间一般为0.3~0.5 s[16]。 基于相量测量单元PMU(Phasor Measurement Unit)的WAMS为电力系统动态监视、分析与控制创造了良好的条件,使电力系统监控提升到实时动态监测水平[17]。PMU实时采集的发电机角速度正是本文所需角速度[18]。本文所提出的最佳重合闸时间整定方法依赖于等值角速度的变化趋势,若能预测出等值角速度的极小值,就能实现最佳重合闸时间的在线整定。 预测方法中较为成熟的是对PMU实测数据基于泰勒级数展开思想进行曲线拟合的多项式预测以及自回归分析方法等[16,19-20],这些外推预测方法依据实测数据构建拟合模型,并利用滚动数据窗修正拟合系数,在此基础上预测数据发展趋势。然而,此类方法没有很好地对研究对象的物理本质特征进行分析,且滚动数据窗确定的极值点具有不确定性。为避免这些问题,考虑到故障后发电机角速度随时间呈衰减振荡趋势,本文基于文献[21]提出的适用于衰减振荡曲线的预测方法,对等值角速度表达式进行数学变换,进而拟合等值角速度曲线参数,预测其变化趋势确定最佳重合闸时间。详细推导说明如下。 故障后发电机角速度是随时间变化衰减的三角函数曲线[20]。等值角速度亦是如此,并且等值角速度稳态分量为0,这样的变换更利于拟合求解[21]过程,表达式如下: 其中,a与b分别为系统振荡模态的振荡频率与衰减系数。对上式等号左右两边同时求导可得到: 令式(10)中,可由下式近似估计: 其中,var为求方差函数。 c值较小,对拟合各系数产生的影响不大,故忽略 c,且令: 在直角坐标系中,绘制 ω(t)、y(t),观察得知其为中心不在原点的螺旋线,因此可用以下步骤拟合出ω(t)中的变量 B、b、a、φ。 具体拟合求解过程如下: 可得到: 其中,r、t为已知量;B与b可由最小二乘法求解。 与此同时: 其中,t、y、x已知;a与φ可由最小二乘法求解。 至此求得 B、b、a、φ,可直接拟合曲线。 在满足重合闸最小间歇时间的前提下,若能获取足够的信息量生成此对数螺旋线,再采用上述拟合算法,对等值角速度曲线各个参数直接进行拟合,就能预测出等值角速度曲线的极小值,从而在线整定出最佳重合闸时间。 需要指出的是,上述数学推导都是基于表达式(9)得出的,即采集的数据必须要反映振荡曲线这一特点,才能有效运用此拟合方法。因此,为反映振荡曲线特征,数据窗必须包含故障切除后等值角速度出现的第1个极大值和极小值。考虑到故障切除后的一小段时间里,角速度值波动不会很平滑且数据越多越利于拟合,但数据过多并不会对拟合结果有太大改进,为保证预测结果的有效性以及准确性,本文经过多次仿真验证,认为选取以故障切除后一小段时间为开始时间的包含有极大值和极小值的合适数据窗即可。 在仿真软件MATLAB/Simulink中搭建如图2所示的单机无穷大系统模型,动作时序说明如下:0.1 s时在F1处发生永久性三相短路接地故障,0.1 s后故障切除,此后断路器重合,后加速保护启动0.1 s后跳开断路器,故障再次被切除。 图2 单机无穷大系统Fig.2 One-machine infinite-bus system 图3说明了未重合以及不同重合闸时间tRC下发电机转子角速度响应曲线,图中,角速度为标幺值。仿真结果验证了上述理论分析。发电机转子角速度最小时(tRC=0.475 s,1.25 s)重合闸,其振荡程度比断路器闭锁不重合的情况下更轻微。而在转子角速度最大时(tRC=0.83 s)重合闸,其将剧烈振荡,容易引发后续摆失稳,严重影响系统稳定。 图3 不同重合闸时间下的转子角速度响应曲线Fig.3 Response curves of rotor angular velocity for different reclosing times 不同重合闸时间下的稳定指标W如表1所示。从表中可看出,稳定指标W分别在0.475 s和1.25 s时达到了极小值,0.83 s时达到极大值,与前文理论分析结果互为验证。指标的数值大小和变化趋势能反映不同重合闸时间下系统的暂态稳定程度,是较为有效合理的指标。 表1 不同重合闸时间下的稳定指标Table1 Stability indexes for different reclosing times 本文选取0.5 s作为重合闸最小间歇时间,故单机无穷大系统F1处发生永久性三相短路接地故障的最佳重合闸时间为1.25 s。 在仿真软件MATLAB/Simulink中搭建IEEE 3机9节点系统模型如图4所示。分别设置母线5、7,母线4、5,母线4、6之间的单回线路发生故障。 图4 3机9节点系统仿真模型Fig.4 Simulation model of 3-machine 9-bus system 本文以F1处故障为例进行详细分析。设定0.1 s发生永久性三相短路接地故障,故障持续0.1 s后被切除,重合闸选取三相一次自动重合闸方式,重合闸失败后经过0.1 s继电保护装置再次动作,断开三相断路器。 计算故障发生时各发电机的加速功率和惯性时间常数之比 Pace,i/TJi,可识别出第 2、3 号机组为临界机群。故障切除后等值系统中的绝对动能变化曲线如图5所示,图中等值绝对动能为标幺值。 由图5可知,等值绝对动能分别达到极小值对应的时刻为0.425 s与1.275 s,由于重合闸的最小间歇时间为0.5 s,故整定F1处0.1 s发生永久性三相短路接地故障时,对应的最佳重合闸时间为1.275 s。 图5 等值系统绝对动能曲线Fig.5 Absolute kinetic energy curve of equivalent system 本文从不同重合闸时间下稳定指标的变化(结果见表2)和最佳重合闸时间的性质(结果见图6)两方面出发验证此重合闸时间确为最佳重合闸时间。 表2 不同重合闸时间下的稳定指标值Table2 Stability indexes for different reclosing times 图6 不同情况下第1、2号发电机间的功角差Fig.6 Power-angle difference between G1and G2 for different cases 表2表明,tRC=1.275 s时,本文所建立的稳定指标数值极小。从稳定指标值的变化趋势中,可看出在1.275 s进行重合闸操作,极大提高了系统暂态稳定性。由图6可见,故障切除后,系统未失稳于重合闸动作(功角差小于 180°[22])。 按本文所确定的最佳重合闸时间进行重合闸操作,相比于断路器直接闭锁情况能够有效平息主要发电机(对F1处故障,选择1号发电机和临界机群中的第2号发电机)间的功角摇摆,有效降低了系统的振荡幅度。 类似地,可分析得出F1、F2、F3处发生不同类型永久性故障时,对应的最佳重合闸时间如表3所示。 按照本文方法所确定的最佳重合闸时间进行重合闸操作,对不同故障类型都能适用,具有有效抗御重合于永久性故障的能力,其没有加重系统摇摆,反而阻尼了系统的摇摆程度,明显提高了系统的暂态稳定性。 本文以0.1 s为数据段时间长度,数据窗开始时间为故障切除后0.1 s,数据窗终止时间为有第1个极大值的数据段的后0.2 s。以F1处发生永久性三相短路接地故障为例,按照上述数据窗确定原则,采用Simulink仿真所得的(0.3 s,1.1 s)数据。拟合参数值为 B=0.0116、b=0.4963、a=7.6077、φ=-0.2883,能有效预测出等值角速度变化趋势,整定得出最佳重合闸时间为1.275 s,实现了角速度变化趋势的成功预测,提前0.175 s获得了最佳重合闸时间,满足时延要求(通常小于 0.1 s[16]),如图7 所示。 表3 不同故障类型下的最佳重合闸时间Table 3 ORCT for different fault types 类似可得出F1、F2、F3处发生不同类型永久性故障时,在线整定的最佳重合闸时间如表4所示。 表4 最佳重合闸时间在线整定效果Table 4 Effect of online ORCT setting 从稳定指标的值可看出,拟合预测所产生的些许误差对重合闸后系统的稳定程度影响不大。此方法能预测出角速度曲线变化趋势,满足时延和误差允许范围,可实现最佳重合闸时间的在线整定。 实际工程与理论研究中,研究永久性故障的最佳重合闸时间可以达到提高系统暂态稳定性和极大程度发挥重合闸作用的目的。本文以转子角速度为研究视角,对永久性故障最佳重合闸条件进行简化,建立了可结合WAMS实测数据在线预测的等值系统绝对动能判据,从而提出一种永久性故障最佳重合时间的在线整定方法。结果表明,按照该方法整定重合闸时间能有效阻尼系统摇摆,提高系统暂态稳定性。拟合算法所需数据量小,误差小,速度快,能够满足在线要求,有效预测出最佳重合闸时间。然而,数据窗确定方法的理论研究尚有不足,有待进一步的深入探索。 [1]贺家李,李永丽,董新洲,等.电力系统继电保护原理[M].4版.北京:中国电力出版社,2010:238-240. [2]张保会,雷敏,袁宇春.优化重合闸时间提高网络传输能力[J].继电器,1998,26(1):17-21.ZHANG Baohui,LEI Min,YUAN Yuchun.Optimizing the reclosing time to improve the transmission capacity of power network [J].Relay,1998,26(1):17-21. [3]YAGAMI M,MURATA T,TAMURA J.An analysis of optimal reclosing for enhancement of transient stability[J].Electrical Engineering in Japan,2004,147(3):32-39. [4]SADI M A H,ALI H.Combined operation of SVC and optimalreclosing of circuit breakers for power system transient stability enhancement[J].Electric Power Systems Research,2014,106:241-248. [5]宋国兵,索南加乐,孙丹丹.输电线路永久性故障判别方法综述[J].电网技术,2006,30(18):75-80.SONG Guobing,SUONAN Jiale,SUN Dandan.A survey on methods to distinguish permanentfaultsfrom instantaneousfaultsin transmission lines[J].Power System Technology,2006,30(18):75-80. [6]张保会.电网继电保护与实时安全性控制面临的问题与需要开展的研究[J].电力自动化设备,2004,24(7):1-6.ZHANG Baohui.Problems on protection relay&urgency control system in interconnected power network of China and studies needed[J].Electric Power Automation Equipment,2004,24(7):1-6. [7]张保会,郝治国,Zhiqian BO.智能电网继电保护研究的进展(二)——保护配合方式的发展[J].电力自动化设备,2010,30(2):1-4.ZHANG Baohui,HAO Zhiguo,Zhiqian BO.Development of relay protection for smart grid(2):development of protection cooperation mode[J].Electric Power Automation Equipment,2010,30(2):1-4. [8]袁宇春,张保会,阎海山.多机电力系统中重合闸最佳时刻的研究(第2部分):永久性故障最佳重合时刻的研究[J].电力系统自动化,1998,22(6):46-48.YUAN Yuchun,ZHANG Baohui,YAN Haishan.Study on the optimal reclosing time in multi-machine power system.Part two:study on the optimal reclosing time at permanent fault[J].Automation of Electric Power Systems,1998,22(6):46-48. [9]吴洋,张保会.优化重合闸时刻的策略与效益[J].电力自动化设备,2002,22(8):12-15.WU Yang,ZHANG Baohui.Strategy and benefit of optimizing reclosing time[J].Electric Power Automation Equipment,2002,22(8):12-15. [10]张保会,康小宁,薄志谦.发电厂送出线重合闸时机的优选与捕捉[J].中国电机工程学报,1995,15(3):173-178.ZHANG Baohui,KANG Xiaoning,BO Zhiqian.Optimal autoreclosure and its application technique[J].Proceedings of the CSEE,1995,15(3):173-178. [11]张保会,袁越,薄志谦.最佳重合闸时间及其整定计算[J].中国电力,1995,28(2):12-17.ZHANG Baohui,YUAN Yue,BO Zhiqian.Optimalreclosing time and its setting calculation[J].Electric Power,1995,28(2):12-17. [12]袁宇春,张保会.基于EEAC的重合闸最佳时刻的计算[J].电力系统自动化,1999,23(17):10-12.YUAN Yuchun,ZHANG Baohui.Calculationoftheoptimal reclosing time based on EEAC[J].Automation of Electric Power Systems,1999,23(17):10-12. [13]蔡国伟,白宪庆,辛鹏,等.基于网络信息的永久性故障重合闸优化时间整定方法[J].中国电力,2007,40(8):26-31.CAI Guowei,BAI Xianqing,XIN Peng,et al.Setting method on the optimal reclosing time for a permanent fault based on network dynamic variables[J].Electric Power,2007,40(8):26-31. [14]闵勇,李函,林姿峰.转子绝对动能增量及其在失稳模式判别中的应用[J].清华大学学报:自然科学版,2003,43(9):1161-1164.MIN Yong,LI Han,LIN Zifeng.Absolute kinetic energy increment of the generator rotor for distinguishing unstable modes[J].Journal of Tsinghua University:Science and Technology Edition,2003,43(9):1161-1164. [15]刘天琪,邱晓燕,李华强.现代电力系统分析理论与方法[M].北京:中国电力出版社,2007:237-239. [16]刘培,杨军,陶丁涛.一种输电线路瞬时故障最佳重合闸时刻实用计算方法[J].电网技术,2013,37(3):635-640.LIU Pei,YANG Jun,TAO Dingtao.Practical online calculation of optimal reclosing time for transmission line under transient fault[J].Power System Technology,2013,37(3):635-640. [17]鞠平,郑世宇,徐群,等.广域测量系统研究综述[J].电力自动化设备,2004,24(70):37-40,49.JU Ping,ZHENG Shiyu,XU Qun,et al.Survey of wide area measurement system[J].Electric Power Automation Equipment,2004,24(70):37-40,49. [18]刘道伟,马世英,李柏青,等.基于响应的电网暂态稳定态势在线量化评估方法[J].中国电机工程学报,2013,33(4):85-95.LIU Daowei,MA Shiying,LI Baiqing,et al.Quantitative method for on-line power system transient stability assessment based on response information[J].Proceedings of the CSEE,2013,33(4):85-95. [19]张保会,杨松浩,王怀远.电力系统暂态稳定性闭环控(三)——基于预测响应的暂态不稳定闭环控制启动判据[J].电力自动化设备,2014,34(10):1-6.ZHANG Baohui,YANG Songhao,WANG Huaiyuan.Closed-loop control of power system transient stability(3):initiation criterion of transient stability closed-loop control based on predicted response of power system[J].Electric Power Automation Equipment,2014,34(10):1-6. [20]宋方方,毕天姝,杨奇逊.基于WAMS的电力系统受扰轨迹预测[J].电力系统自动化,2007,30(23):27-32.SONG Fangfang,BI Tianshu,YANG Qixun.Perturbed trajectory prediction method based on wide area measurement systems[J].Automation of Electric Power Systems,2006,30(23):27-32. [21]DING L J,FAN H.BOCS based power system stability margin estimation[J].Advanced Materials Research,2013,2694(805):693-699. [22]谭伟,沈沉,刘锋,等.基于轨迹特征根的暂态稳定实用判据[J].电力系统自动化,2012,36(16):14-19.TAN Wei,SHEN Chen,LIU Feng,et al.A practical criterion for trajectory eigenvalues based transient stability analysis[J].Automation of Electric Power Systems,2012,36(16):14-19.2 最佳重合闸时间整定判据
2.1 等值绝对动能判据




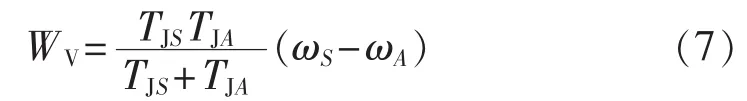
2.2 稳定指标
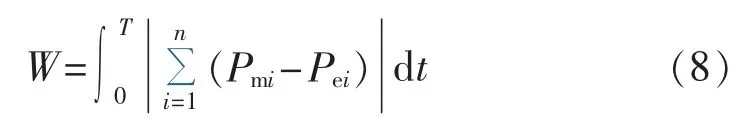
3 最佳重合闸时间的在线整定
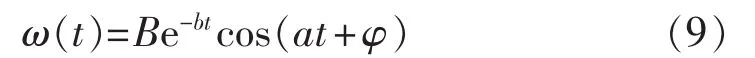
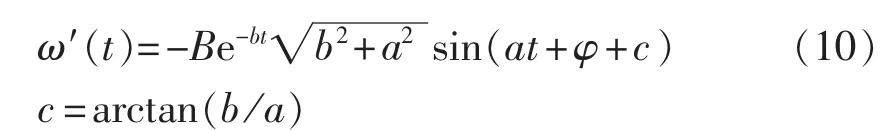



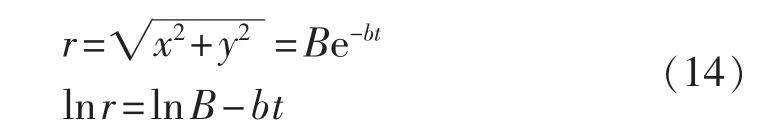
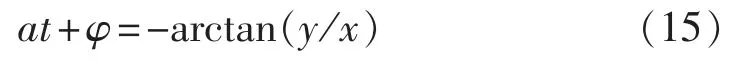
4 仿真与分析
4.1 单机无穷大系统仿真


4.2 3机9节点系统仿真

4.3 最佳重合闸时间的在线整定

5 结论

