含VSC-HVDC交直流混合系统机电暂态仿真研究

张 芳 ，李静远 ，李传栋

（1.天津大学 智能电网教育部重点实验室，天津 300072；2.福建省电力有限公司电力科学研究院，福建 福州 350007）

0 引言

基于电压源型变流器的高压直流输电VSCHVDC（Voltage Source Converter based High Voltage Direct Current）技术在世界上已得到实际应用［1］。 其相对于传统直流输电技术，具有以下特点［2-5］：可独立控制有功和无功功率传输；可向弱交流电网及无源系统供电且无需站间通信；潮流反转时电压极性不变；采用脉宽调制 PWM（Pulse Width Modulation）技术，输出电压低次谐波含量减少。因此VSC-HVDC特别适合于大规模风力发电的并网［6-7］、城市供电和异步交流电网互联等场合。由于电力电子元件的存在，对于VSC-HVDC适合采用电磁暂态仿真研究其动态特性，但受仿真速度和系统规模的限制，电磁暂态仿真不适合研究大规模交直流混合系统［8-9］；而机电暂态仿真能在保证一定计算精度的情况下提高仿真速度，以模拟直流系统与交流电网之间的相互作用，因此有必要建立VSC-HVDC机电暂态仿真模型，深入研究VSC-HVDC系统的控制策略和运行特性。

目前，对于VSC-HVDC系统的控制策略主要分为间接控制和直接控制。间接控制即通过控制VSC交流侧电压基波幅值和相角来达到控制目标［9-11］，该方法结构简单，但存在电流动态响应慢的缺点。目前工业中占主导地位的直接控制通常由外环功率、电压控制和内环电流控制2个环构成，具有快速电流响应特性和限流能力：文献［12-16］基于比例积分PI（Proportional Integral）控制方法在dq旋转坐标系下建立VSC-HVDC双环控制模型，实现独立调节有功功率（或直流电压）、无功功率（或交流电压）的目的，该方法具有算法简单、可靠性强和易于实现的特点，但在dq旋转坐标系下，内环电流解耦控制器需添加前馈补偿以抵消VSC数学模型中交叉耦合项的影响，降低了控制系统的鲁棒性。文献［17-18］基于反馈线性化控制思想设计内环电流控制器，实现了d、q分量的解耦控制。文献［19］将自抗扰控制技术引入到VSC-HVDC系统中，避免了控制系统对复杂数学模型的过度依赖。

比例谐振 PR（Proportional Resonant）控制在电机和光伏逆变器控制中应用较多［20-22］，文献［23-24］将PR控制应用于VSC-HVDC电磁暂态仿真，本文将PR控制引入VSC-HVDC机电暂态仿真模型中，改进了内环电流控制器的设计，可以实现系统模型的完全解耦。为详细模拟直流系统的快速动态，采用双时步混合仿真方法实现含VSC-HVDC交直流系统仿真，即交流系统采用隐式梯形积分法计算，而直流系统采用改进欧拉法计算；最后通过算例验证所建模型和仿真算法的正确性和有效性。

1 VSC-HVDC机电暂态数学建模

1.1 VSC-HVDC交流侧数学模型

本文只考虑交流系统基波分量，建立VSC-HVDC机电暂态模型。双端VSC-HVDC系统结构如图1所示。图中，R1、R2分别为联结变压器和相电抗器的等效电阻以及VSC内部损耗；L1、L2分别为联结变压器和相电抗器的等效电感；Usi∠θsi、Uci∠（θsi+δi）（i=1，2）分别为公共耦合点PCC（Point of Common Coupling）电压、VSC输出电压的基频分量，δ为Uc相对于Us的移相角度；Psi、Qsi、Pci分别为交流电网侧有功、无功以及VSC侧有功功率；isi为由交流电网侧流向VSC的电流；Cdc为 VSC直流侧电容；Rdc、Ldc分别为直流线路的电阻、电感。

图1 双端VSC-HVDC系统结构图Fig.1 Structure of two-terminal VSC-HVDC system

图2为单端VSC结构图，为实现VSC-HVDC解耦控制，首先建立dq同步旋转坐标系下VSC交流侧数学模型：

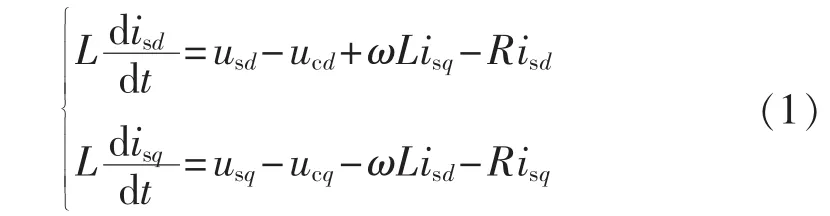
其中，isd、isq分别为电网电流的 d、q 轴分量；usd、usq分别为PCC处电网电压的d、q轴分量；ucd、ucq分别为VSC侧基波电压的d、q轴分量。

图2 单端VSC结构图Fig.2 Structure of one-terminal VSC

由式（1）可知，在同步旋转坐标系下VSC数学模型存在d、q轴电流耦合项，该耦合项大小与同步旋转角频率ω和电感参数L相关，在实际工程中，电感存在饱和现象，其电感值会随电流变化呈非线性变化，传统PI控制中以恒定电感参数进行补偿，无法实现电流内环的精确解耦，从而降低了控制系统的鲁棒性［20］。

现建立αβ静止坐标系下VSC交流侧数学模型：

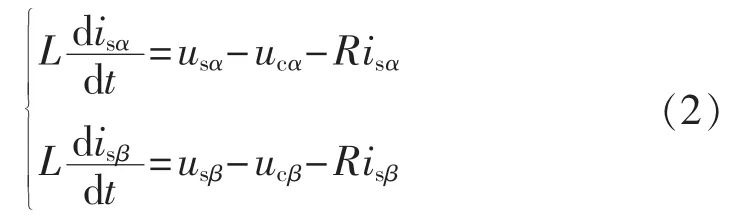
其中，各电压、电流量分别表示相应的α、β轴分量。可以看出，该数学模型中α、β轴方程分别只含有各自坐标轴上的变量，不存在电流耦合项，α、β轴之间是完全解耦的。

1.2 VSC-HVDC直流侧数学模型

VSC-HVDC直流侧电路包括VSC侧直流电容和直流线路，如图3所示。直流侧数学模型如下：

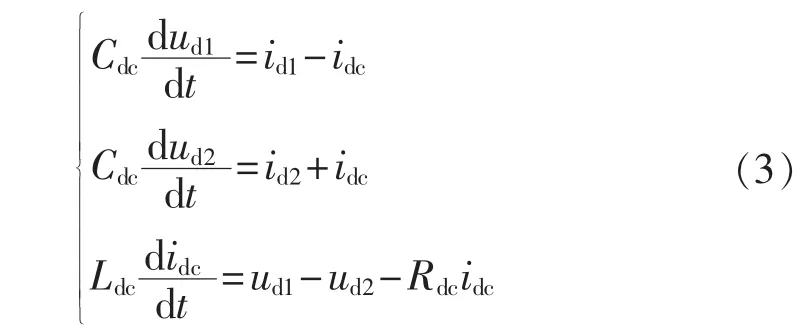
其中，idi、udi（i=1，2）分别为两侧 VSC 直流电流和电压。因VSC的内部损耗在电阻R中计及，故VSC侧有功功率Pc等于VSC注入直流侧的功率Pdc，因此有如下等式：

则直流侧电流为：

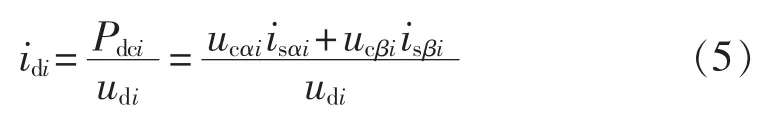
将式（5）中的 idi（i=1，2）代入式（3）中进行计算。

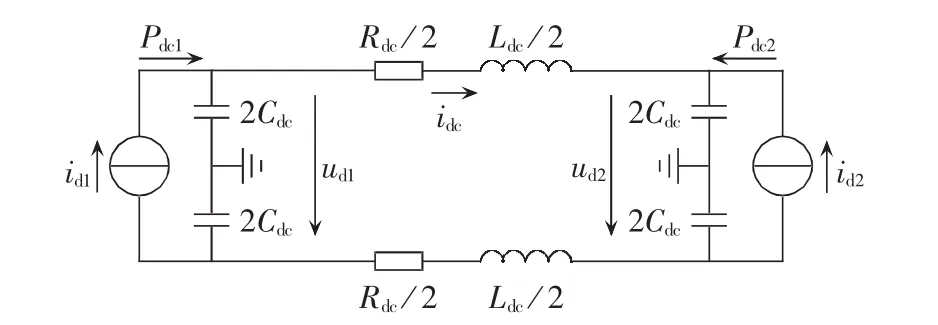
图3 VSC-HVDC直流侧等效电路图Fig.3 Equivalent DC-side circuit of VSC-HVDC

2 VSC-HVDC控制模型

2.1 基于PR控制的内环控制器

PR控制器是由比例环节和广义积分GI（Generalized Integral）环节组成，其传递函数如下［21］：

其中，Kp、Kr分别为比例和积分时间系数；ω0为谐振频率。当输入信号角频率为ω0时，PR控制器增益为无穷大，可以实现正弦输入信号的无静差跟踪，类似于PI控制的积分器在0 Hz处增益无穷大。

式（6）中的广义积分环节可分解为如下2个简单的积分器：

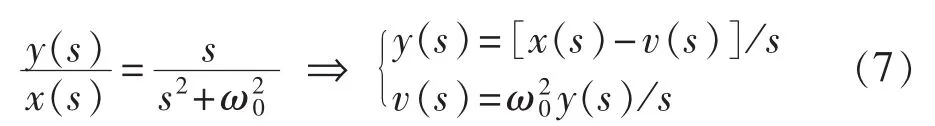
其中，x、y分别为广义积分环节的输入、输出量；v为输出反馈量。为便于程序实现，式（7）可由图4所示框图表示。

由上述可知，PR控制可对角频率为ω0的交流信号进行无静差跟踪，因此可将PR控制器引入到αβ坐标系下的内环电流控制器中，如图5所示。

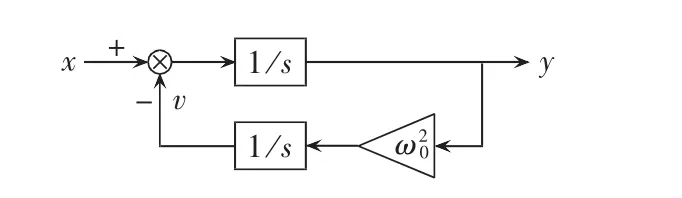
图4 广义积分项分解示意图Fig.4 Schematic diagram of GI decomposition

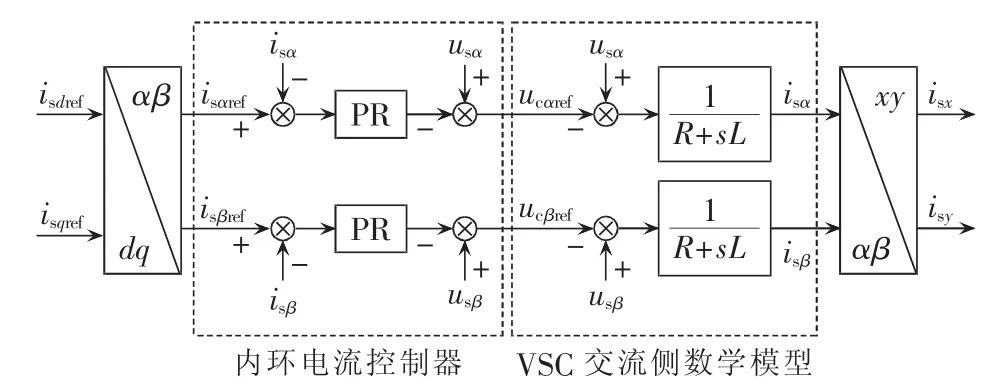
图5 基于PR控制的内环电流控制器Fig.5 Inner-loop current controller based on PR control

图5 中，isαref、isβref分别为内环电流参考值的 α、β轴分量，是由外环控制器输出的d、q轴电流参考值isdref、isqref经 dq/αβ 变换得到；isα、isβ分别为内环电流的α、β 轴分量；usα、usβ分别为 PCC 电网电压的 α、β 轴分量；ucαref、ucβref分别为内环控制器输出的 VSC 电压参考值的α、β轴分量；isx、isy分别为交流电网向VSC传输电流相量的实、虚部。现以α轴为例，根据式（6）和式（7）列写内环电流控制器方程：

再根据式（2）计算出 isα、isβ，经过 αβ/xy 变换可得出 isx、isy，按照图1 所示参考方向，-isx、-isy即为 VSC向PCC的节点注入电流。

基于dq同步旋转坐标系下的传统内环电流PI控制器如图6所示［12-15］。对比图5和图6可见，基于PR控制的内环电流控制器能有效跟踪指定频率的交流信号，设置ω0为电网电压基波角频率，可以实现对内环电流参考值的无静差跟踪；同时αβ坐标系下的控制器模型无交叉耦合项，因此可以实现精确解耦。

图6 基于PI控制的内环电流控制器Fig.6 Inner-loop current controller based on PI control

2.2 外环控制器

外环控制器向内环控制器提供交流侧电流的d、q轴分量的电流参考值isdref、isqref。为了保持有功平衡和直流电压稳定，VSC-HVDC必须有一侧变流器采用定直流电压控制，而另一侧变流器根据需要选择定有功、无功或交流电压控制。

2.2.1 有功、无功功率控制器

将PCC电压Us定向于同步旋转d轴，根据瞬时功率理论，VSC从电网吸收的有功和无功功率为：

由上式可知，改变电流参考值isdref、isqref即可分别独立地控制交流电网与VSC-HVDC之间传输的有功和无功功率。现采用开环和PI环节组合方式设计有功、无功功率控制器，控制器方程如下：

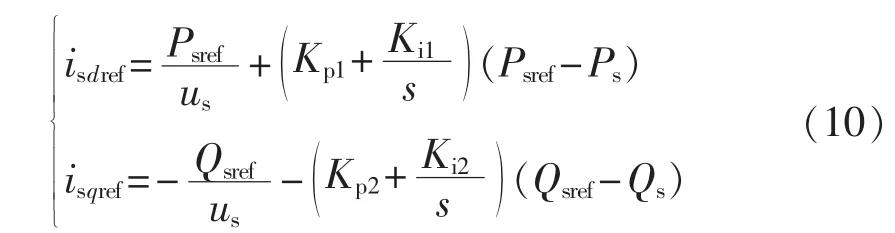
引入新的状态变量N1、N2，其时域的微分方程如式（11）所示［15］：

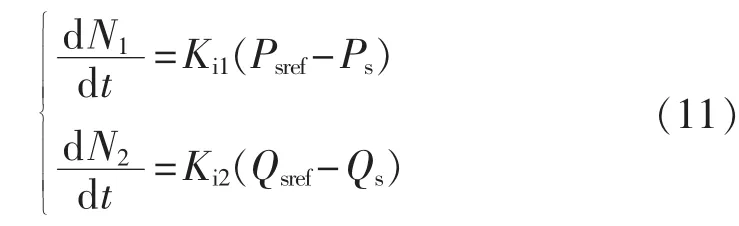
则式（10）可化为：

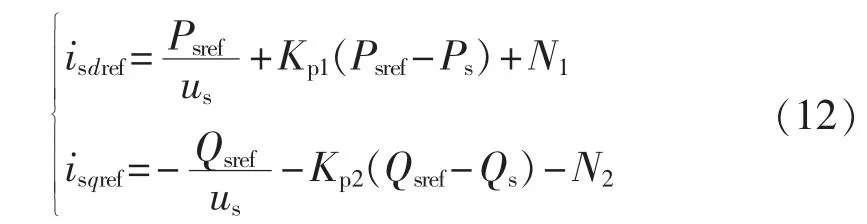
2.2.2 交流电压控制器

VSC-HVDC也可采用定交流电压控制替换无功功率控制，其控制器方程如下：

同理引入变量N3，可得：

2.2.3 直流电压控制器

在不考虑交流线路和VSC内部损耗的条件下，VSC交直流两侧有功功率相等，有如下等式：

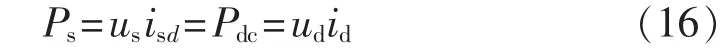
当VSC-HVDC两侧变流器传输的有功不平衡时，将引起直流侧电容电压波动，控制有功电流isd向直流电容充电（或放电），可以保持直流电压ud稳定在参考值udref。因此根据式（16），设计如下直流电压控制器：

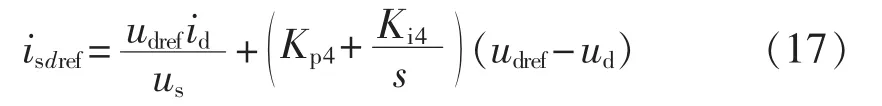
同理引入变量N4，其微分方程如下：

则式（17）可化为：

3 VSC-HVDC交直流系统机电暂态仿真算法

对于含VSC-HVDC的大型交直流系统联合仿真，一方面需要修改PCC对应的节点电流方程及其雅可比矩阵元素，另一方面还需要增加直流输电线路方程，因此VSC-HVDC系统模型的增加使得原交流系统机电暂态程序代码结构变动较大［11］。本文采用VSC-HVDC系统与交流系统交替求解的方法，即交流电网计算主程序与VSC-HVDC子程序之间交替求解。

交替求解过程中，VSC-HVDC系统通过控制由VSC流入两侧PCC的注入电流相量实现与交流电网的相互作用。每一积分时刻交流电网主程序向VSC-HVDC子程序输入PCC电压幅值和相角，子程序依次计算外环控制器、内环控制器、VSC数学模型及直流输电线路方程，计算VSC-HVDC各个状态变量和PCC的注入电流相量的更新值，并将注入电流相量返回交流电网主程序，求解下一积分时刻PCC电压。

考虑到直流系统中电感、电容的存在，为详细模拟直流系统的快速动态，VSC-HVDC系统采用改进欧拉法进行积分计算，步长Δt=50 μs，改进欧拉法为显式积分方法，虽然采用小步长积分，但积分速度很快；而交流系统采用隐式梯形积分法计算，步长ΔT=0.01 s。由于VSC-HVDC和交流系统积分方法精度均为二阶，因此当时，其组合后的双时步混合仿真方法收敛，收敛阶为二阶［25］。采用双时步混合仿真时，需考虑小步长积分时刻母线电压的读取问题：文献［11］采用插值法，即根据t-ΔT时刻的读取电压与t时刻的预估电压，按照主程序求解步长与子程序小步长的倍数关系等分，采用线性插值求每一个小步长积分时刻对应的电压；由于整个交流系统积分步长较小，本文假设在VSC-HVDC小步长仿真过程中VSC母线电压不变［26］。算法流程如图7所示。

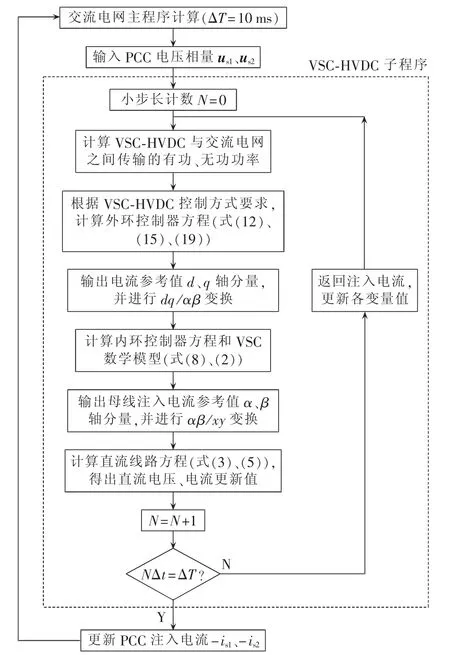
图7 含VSC-HVDC交直流混合系统暂态仿真流程Fig.7 Flowchart of transient simulation of AC /DC hybrid system containing VSC-HVDC

4 VSC-HVDC仿真分析

为验证本文所提VSC-HVDC控制模型的正确性，基于PSASP/UPI功能编写VSC-HVDC子程序，在新英格兰39节点系统上进行仿真实验。原系统母线14与母线4之间为交流线路，现将该交流线路替换为VSC-HVDC，如图8所示。母线14和母线4分别接VSC1和 VSC2。

VSC-HVDC系统参数如下：基准容量100 MV·A；VSC1侧和VSC2侧联结变压器的变比分别为230 kV/100 kV 和 100 kV/230 kV，R1=R2=0.002 p.u.，X1=X2=0.3 p.u.；直流电压±100 kV，直流线路电阻Rdc=5.5 Ω，电感 Ldc=64 mH，电容 Cdc=160 μF。 VSC1采用定有功Ps1和定无功功率Qs1控制，VSC2采用定直流电压Ud2和定无功功率Qs2控制，分别采用本文所提的基于PR控制的内环控制器和图6所示的基于PI控制的内环控制器进行仿真对比，下文为表述简便，将上述2种方法分别简称为PR控制和PI控制，2种方法的外环控制器相同，内、外环控制器参数分别如表1和表2所示。

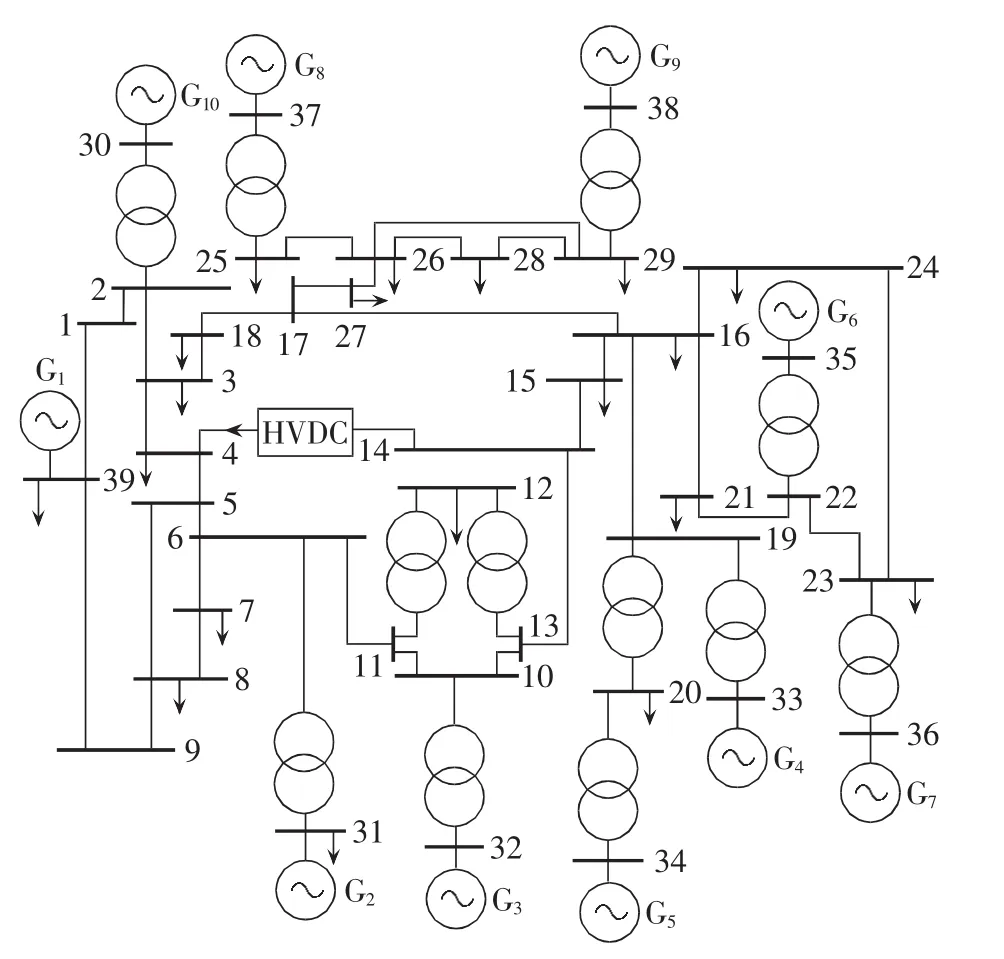
图8 新英格兰系统图Fig.8 Diagram of New England system

表1 VSC-HVDC内环控制器参数Table1 Parameters of VSC-HVDC inner-loop controller

表2 VSC-HVDC外环控制器参数Table 2 Parameters of VSC-HVDC outer-loop controller

4.1 有功功率阶跃响应

VSC2侧直流电压参考值为2 p.u.，两侧VSC传输无功功率均保持在0；0.5 s时，VSC1侧有功功率参考值由-1 p.u.阶跃至-2 p.u.；1.5 s 时，VSC1侧有功功率参考值由-2 p.u.反转至2 p.u.。图9给出有功、无功功率及直流电压、电流变化曲线。

由图9可见，VSC1有功功率发生阶跃和潮流反转，VSC2能根据相应的功率变化改变传输功率，此时两侧VSC传输无功功率几乎无影响，只有微小波动，说明了2种方法能够实现有功、无功功率的独立控制；采用PR控制和PI控制在有功、无功功率控制方面效果相当，而对于直流电压控制，由于PR控制中的电流内环不存在耦合项，改善了整个控制系统鲁棒性，因而超调量较小，收敛速度更快。

4.2 无功功率阶跃响应

VSC1侧有功功率参考值保持在2.0p.u.，0.5s时传输无功功率由0阶跃至0.5 p.u.；VSC2侧直流电压稳定在2.0 p.u.，1.5 s时无功功率由0阶跃至-0.4 p.u.。有功、无功功率及PCC母线电压曲线如图10所示。

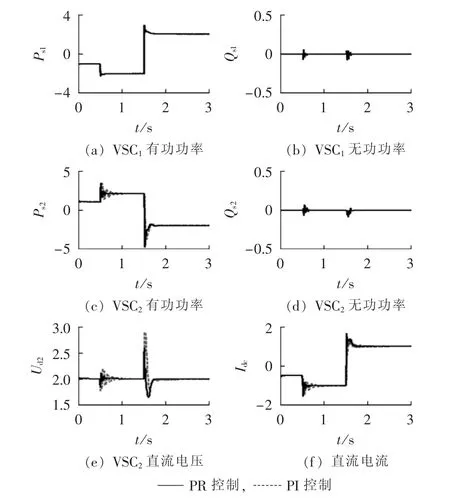
图9 有功功率阶跃时响应Fig.9 Response to step change of active power

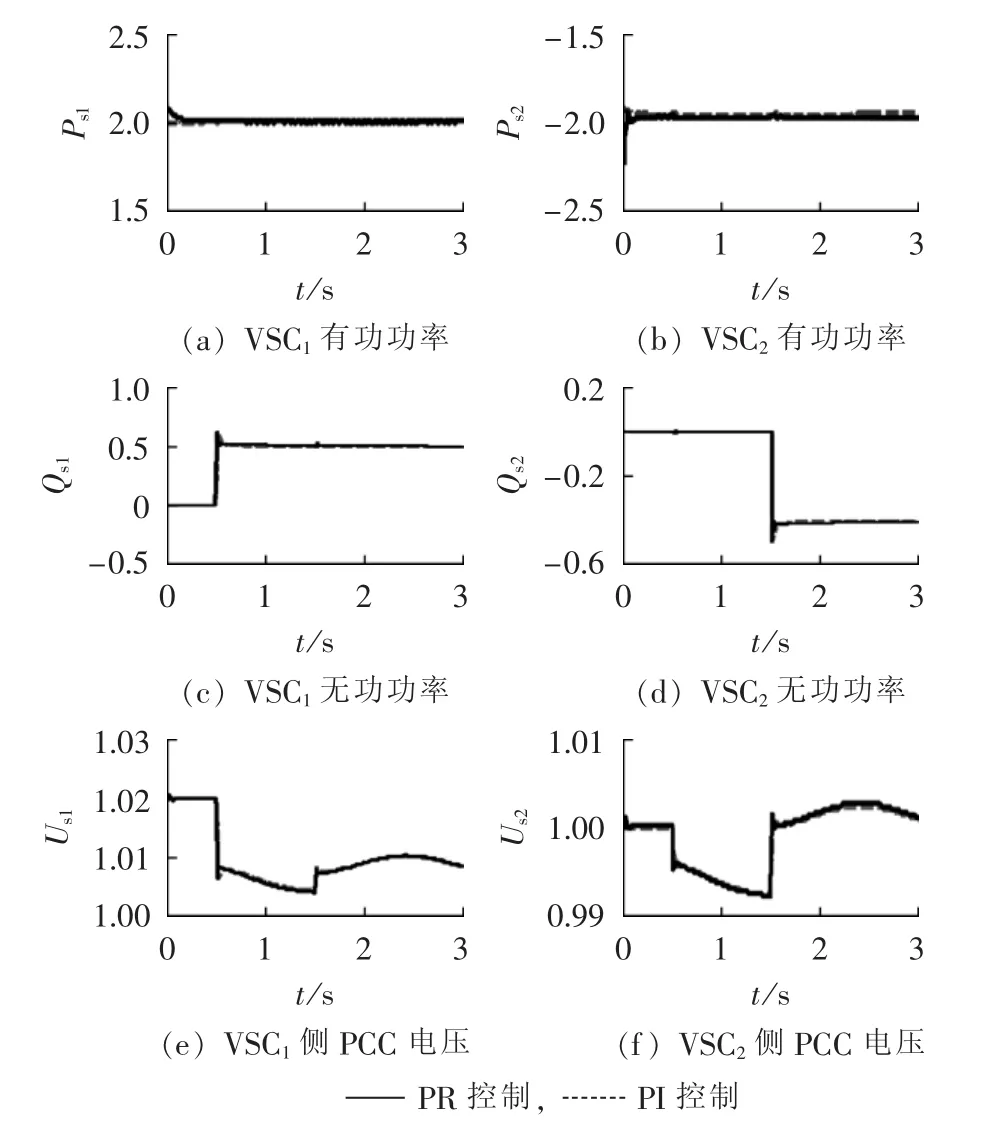
图10 无功功率阶跃时响应Fig.10 Response to step change of reactive power

由图10可知，采用PR控制和PI控制效果基本相同：0.5 s时VSC1侧无功功率阶跃至0.5 p.u.，表明VSC1从交流电网吸收无功，因而VSC1侧PCC母线电压会有所下降；同样1.5 s时VSC2侧无功功率阶跃至-0.4 p.u.，表明VSC2向交流电网注入无功，进而抬升VSC2侧PCC母线电压；又由于整个系统的互联，VSC1和VSC2两侧PCC母线电压相互影响产生如图10所示同升同降的曲线变化。两侧VSC传输无功功率依次发生阶跃时，VSC-HVDC与交流电网间传输的有功功率能够保持在参考值，且两侧VSC无功功率传输互不影响，进一步验证了采用本文所提的控制策略时VSC-HVDC系统能够实现有功、无功功率解耦控制，以及两侧VSC无功控制的相互独立。

4.3 直流电压阶跃响应

VSC1侧有功、无功功率参考值分别保持在2.0 p.u.、0.5 p.u.，VSC2侧无功功率参考值保持在 -0.4 p.u.。1.5 s时，VSC2直流电压参考值由2.0 p.u.阶跃到2.2 p.u.，有功功率及直流电压、电流变化曲线如图11所示。

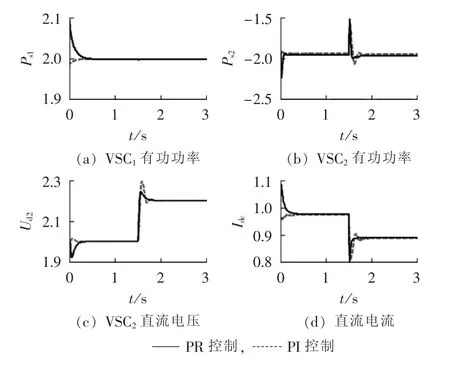
图11 直流电压阶跃时响应Fig.11 Response to step change of DC voltage

在0～0.3 s时间内系统处于起步阶段。由图11可知，当直流电压在10%内变化时，采用PR控制器和PI控制器的VSC-HVDC暂态模型均能使系统变量保持在参考值，但PR控制下直流电压收敛速度更快，超调量更小，控制效果优于PI控制，所得结论与4.1节相同。

4.4 双时步混合仿真验证

VSC1侧有功、无功功率参考值分别保持在2.0 p.u.、0.5 p.u.，VSC2侧无功功率、直流电压参考值分别保持在-0.4 p.u.、2.0 p.u.。0.5 s时图8中母线5和6之间联络线上母线5出口处发生三相短路接地故障，0.6 s时故障消失。分别采用本文所提双时步混合仿真方法（方法 1）和文献［11］方法（方法 2）进行仿真比较。仿真曲线如图12所示。

由图12可知，0.5 s发生故障时，VSC2侧 PCC电压瞬间跌落，使得VSC-HVDC两侧功率传输均受影响，但由于VSC1采用定有功功率控制，其从交流电网吸收的有功（1.91 p.u.）大于采用定直流电压控制的VSC2向交流电网注入的有功（0.79 p.u.），VSC2的直流电容充电使得直流电压上升。0.6 s故障消失时，VSC2侧PCC电压瞬间上升，VSC1从交流电网吸收的有功（2.17 p.u.）小于VSC2向交流电网注入的有功（4.83 p.u.），VSC2的直流电容放电使得直流电压下降。采用以上2种方法所得仿真曲线大致相同，均能反映交流系统发生故障时VSC-HVDC系统的动态响应。方法1的曲线收敛速度略优于方法2，是因为方法2需先利用插值法对母线电压进行预估。

图12 VSC-HVDC双时步混合仿真曲线Fig.12 Simulative curves of dual time-step simulation for VSC-HVDC

5 结论

本文建立VSC-HVDC交直流混合系统机电暂态仿真模型，模拟了交流电网与VSC-HVDC之间相互作用，以新英格兰系统为例验证了所建模型的正确性和有效性。该模型具有以下优点。

a.针对VSC-HVDC系统在dq同步旋转坐标系下内环电流控制器不能实现精确解耦的问题，引入αβ静止坐标系下的PR控制改进了内环电流控制器，该控制器可以无静差跟踪交流电流信号，并实现内环电流的精确解耦。

b.VSC-HVDC子程序与交流电网主程序交替求解实现交直流系统机电暂态仿真，通过控制注入电流实现交、直流系统的相互作用。采用双时步混合仿真方法详细模拟了直流系统的动态特性，既提高了仿真精度，又保持了较快的仿真速度。

［1］汤广福.基于电压源换流器的高压直流输电技术［M］.北京：中国电力出版社，2010：3-13.

［2］徐政，陈海荣.电压源换流器型直流输电技术综述［J］.高电压技术，2007，33（1）：1-10.XU Zheng，CHEN Hairong.Review andapplicationsofVSC HVDC［J］.High Voltage Engineering，2007，33（1）：1-10.

［3］汤广福，贺之渊，庞辉.柔性直流输电工程技术研究、应用及发展［J］.电力系统自动化，2013，37（15）：3-14.TANG Guangfu，HE Zhiyuan，PANG Hui.Research application and development of VSC-HVDC engineering technology［J］.Automation of Electric Power Systems，2013，37（15）：3-14.

［4］梁海峰，李庚银，李广凯，等.向无源网络供电的VSC-HVDC系统仿真研究［J］.电网技术，2005，29（8）：45-50.LIANG Haifeng，LI Gengyin，LI Guangkai，et al.Simulation study of VSC-HVDC system connected to passive network［J］.Power System Technology，2005，29（8）：45-50.

［5］郑超，滕松，宋新立，等.百万千瓦级柔性直流接入大连电网后的系统特性分析［J］.电力系统自动化，2013，37（15）：15-19.ZHENG Chao，TENG Song，SONG Xinli，et al.Analysis on system characteristics after incorporation of ±320/1 000 MW VSC-HVDC into Dalian Power Grid［J］.Automation of Electric Power Systems，2013，37（15）：15-19.

［6］潘伟，李勇，曹一家，等.用于大规模集中式风电并网的VSCHVDC 频率控制方法［J］.电力自动化设备，2015，35（5）：94-99.PAN Wei，LI Yong，CAO Yijia，et al.Frequency control of gridconnection system based on VSC-HVDC for large-scale centralized wind farm［J］.Electric Power Automation Equipment，2015，35（5）：94-99.

［7］章心因，胡敏强，吴在军，等.基于VSC-HVDC的风力发电系统低电压穿越协调控制［J］.电力自动化设备，2014，34（3）：138-143.ZHANG Xinyin，HU Minqiang，WU Zaijun，et al.Coordinated LVRT control of wind power generation system based on VSC-HVDC［J］.Electric Power Automation Equipment，2014，34（3）：138-143.

［8］汤涌.电力系统数字仿真技术的现状与发展［J］.电力系统自动化，2002，26（17）：66-70.TANG Yong.Present situation and development of power system simulation technologies［J］.Automation of Electric Power Systems，2002，26（17）：66-70.

［9］王冠，蔡晔，张桂斌，等.高压直流输电电压源换流器的等效模型及混合仿真技术［J］.电网技术，2003，27（2）：4-8.WANG Guan，CAI Ye，ZHANG Guibin，et al.Equivalent model of HVDC-VSC and its hybrid simulation technique［J］.Power System Technology，2003，27（2）：4-8.

［10］郑超，盛灿辉，魏强，等.VSC-HVDC输电系统的电磁暂态建模与仿真［J］.高电压技术，2007，33（11）：94-99.ZHENG Chao，SHENG Canhui，WEI Qiang，et al.Electromagnetic transient modeling and simulation for VSC-HVDC［J］.High Voltage Engineering，2007，33（11）：94-99.

［11］郑超.实用柔性直流输电系统建模与仿真算法［J］.电网技术，2013，37（4）：1058-1063.ZHENG Chao.Studyonpracticalmodelingandsimulation algorithm for VSC-HVDC power transmission［J］.Power System Technology，2013，37（4）：1058-1063.

［12］皇甫成，汤广福，阮江军，等.VSC-HVDC统一电磁暂态模型及其控制策略［J］.高电压技术，2008，34（5）：903-908.HUANG Fucheng，TANG Guangfu，RUAN Jiangjun，et al.Unified electromagnetic transient model and control strategy for the voltage source converter based HVDC transmission ［J］.High Voltage Engineering，2008，34（5）：903-908.

［13］陈海荣，张静，潘武略.电压源换流器型直流输电系统的启动控制［J］.高电压技术，2009，35（5）：1164-1169.CHEN Hairong，ZHANG Jing，PAN Wulue.Start-up control of VSC based on HVDC system［J］.High Voltage Engineering，2009，35（5）：1164-1169.

［14］刘昇，徐政，唐庚，等.VSC-HVDC机电暂态仿真建模及仿真［J］.电网技术，2013，37（6）：1672-1677.LIU Sheng，XU Zheng，TANG Geng，etal.Electromechanical transient modeling and simulation for voltage source converter based HVDC power transmission［J］.Power System Technology，2013，37（6）：1672-1677.

［15］COLE S，BEERTEN J，BELMANS R.Generalized dynamic VSC MTDC model for power system stability studies［J］.IEEE Trans on Power Systems，2010，25（3）：1655-1662.

［16］文安，邓旭，魏承志，等.柔性直流输电系统交直流并列运行与孤岛运行方式间的切换控制［J］.电力自动化设备，2014，34（7）：99-106.WEN An，DENG Xu，WEI Chengzhi，et al.Switching control between AC-DC parallel and islanded operations of VSC-HVDC transmission system［J］.Electric Power Automation Equipment，2014，34（7）：99-106.

［17］陈海荣，徐政.向无源网络供电的VSC-HVDC系统的控制器设计［J］.中国电机工程学报，2006，26（23）：42-48.CHEN Hairong，XU Zheng.Controldesign forVSC-HVDC supplying passive network［J］.Proceedings of the CSEE，2006，26（23）：42-48.

［18］严干贵，陈涛，穆钢，等.轻型高压直流输电系统的动态建模及非线性解耦控制［J］.电网技术，2007，31（6）：45-50.YAN Gangui，CHEN Tao，MU Gang，et al.Dynamic modeling and nonlinear-decouple control of HVDC light system［J］.Power System Technology，2007，31（6）：45-50.

［19］范彬，王奔，李新宇.基于自抗扰控制技术的VSC-HVDC系统控制器设计［J］.电力自动化设备，2013，33（5）：65-75.FAN Bin，WANG Ben，LIXinyu.Design ofADRC-based controller for VSC-HVDC system［J］.Electric Power Automation Equipment，2013，33（5）：65-75.

［20］王恩德，黄声华.表贴式永磁同步电机伺服系统电流环设计［J］.中国电机工程学报，2012，32（33）：82-88.WANG Ende，HUANG Shenghua.Current regulator design for surface permanent magnet synchronous motor servo systems［J］.Proceedings of the CSEE，2012，32（33）：82-88.

［21］陈炜，陈成，宋战锋，等.双馈风力发电系统双PWM变换器比例谐振控制［J］.中国电机工程学报，2009，29（15）：1-7.CHEN Wei，CHEN Cheng，SONG Zhanfeng，et al.Proportionalresonant control for dual PWM converter in doubly fed wind generation system［J］.Proceedings of the CSEE，2009，29（15）：1-7.

［22］LIU Bo，YANG Xu，ZHANG Yan，et al.A new control strategy combing PI and quasi-PR control under rotate frame for three phase grid-connected photovoltaic inverter［C］//2011 IEEE 8th International Conference on Power Electronics and ECCE Asia（ICPE&ECCE）.Jeju，Korea：IEEE，2011：882-888.

［23］HUANG Cheng，ZHAO Lihua.Design of controller for VSCHVDC systems with the α β stationary frame［C］//2012 Asia-Pacific Power and Energy Engineering Conference（APPEEC）.Shanghai，China：IEEE，2012：1-4.

［24］胡永银，李兴源，周洪宇，等.应用于VSC-HVDC输电的谐波抑制控制器［J］.电网技术，2014，38（3）：583-588.HU Yongyin，LI Xingyuan，ZHOU Hongyu，et al.A kind of harmonic suppression controller used in VSC-HVDC transmission system［J］.Power System Technology，2014，38（3）：583-588.

［25］刘德贵，费景高.动力学系统数字仿真算法［M］.北京：科学出版社，2000：259-264.

［26］BRANDT R M，ANNAKKAGE U D，BRANDT D P，et al.Validation of a two-time step HVDC transient stability simulation model including detailed HVDC controls and DC line L/R dynamics［C］//2006 IEEE Power Engineering Society General Meeting.Montreal，Canada：IEEE，2006：1-6.