基于附加有功信号的VSC-MTDC系统平衡控制策略

闫文宁 ，李可军 ，王卓迪 ，霍雪松 ，吴海伟 ，张 明，孟新涵

（1.山东大学 电气工程学院，山东 济南 250061；2.国网江苏省电力公司，江苏 南京 210024；3.国网南京供电公司，江苏 南京 210019）

0 引言

随着全控型大容量电力电子器件的问世，柔性直流输电技术在全世界范围内迅速发展，基于电压源型换流器的多端直流输电系统VSC-MTDC（Voltage Source Converter based Multi-Terminal Direct Current）以其输电容量大、可控性好、具备动态无功补偿及改善电能质量等优点成为构建智能电网的重要组成部分，在大规模新型能源中心（如风力、太阳能发电等）输送功率到远方几个负荷中心、向弱交流系统及负荷密集的大城市甚至无源网络供电、不同区域的电力市场交易、孤立交流系统互联、大城市直流电网多落点受电等领域具有广阔的应用前景［1-5］。

为维持VSC-MTDC系统的有功功率的平衡和直流电压的稳定，多端柔性直流系统中同一时刻至少应有一个换流站控制系统的直流电压。当系统中只有一个换流站控制直流电压时，若直流电压控制站交流侧发生故障等大的扰动后，交流电压的跌落使得此站需要更大的电流输出同样的有功功率以维持系统的功率平衡，但是由于限流器的作用，直流电压控制站可能会进入限流模式，失去直流电压的控制能力。此时，由于没有站间通信，若系统中定有功功率APC（Active Power Control）换流站仍按照预先设定的有功功率参考值输出功率，则导致直流网络中的有功缺额得不到有效的支援，直流电压失去控制，最终造成系统退出运行。

为避免出现上述的情况，国内外学者针对直流系统大扰动下的直流电压控制能力进行了广泛研究。国内外普遍的做法是设置直流电压备用控制，或是同一时刻多个换流站共同控制直流电压。主要的控制策略包括裕度控制［6］、下垂控制［7］等。 文献［8］提出一种多点直流电压控制策略，在改善直流电压质量、提高换流器利用率上具有明显优势；文献［9-10］提出了基于直流电压偏差的多点直流电压控制策略，该控制方式在无需通信的情况下，可以保证在主控站退出运行后系统有功功率平衡和直流电压的稳定；文献［11］提出了改进的直流电压偏差斜率控制策略，结合了偏差控制和斜率控制的优点，提高了系统动态响应能力；文献［12］提出了基于直流电压-有功功率特性的多端控制策略，保证了在受到大扰动情况下系统的正常运行；文献［13］提出了基于改进定有功功率控制特性的协调控制策略，有效解决了主导站过载时系统功率不平衡及直流电压失稳问题。

以上研究有效地解决了直流电压控制站故障后直流电压的稳定问题，但是大扰动情况下的直流电压控制多是通过直流电压备用控制实现的，这就导致系统需要频繁切换控制状态，增加了控制系统的复杂程度。

在上述研究基础上，本文提出一种无需通信、不需要模式切换的直流电压控制策略，即在考虑换流站过载及定有功功率换流站可调容量基础上，在定有功功率控制器参考值上叠加由改进有功功率-直流电压特性曲线计算得到的附加有功功率信号，实现定直流电压站故障期间有功功率的平衡及直流电压的稳定，并仿真验证了所提方法的有效性。

1 VSC-MTDC系统结构及建模

本文以图1所示的环形四端VSC-MTDC系统为例，说明协调控制策略的设计与整定方法。

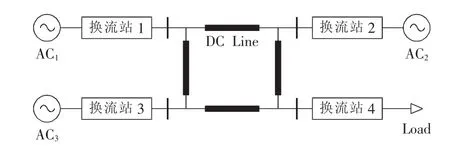
图1 VSC-MTDC系统结构图Fig.1 Structure of VSC-MTDC system

该系统包含4个电压源型换流站，其中，换流站1工作于定直流电压控制方式，连接于交流无穷大系统；换流站2和3工作于定有功功率控制方式，在定直流电压站故障时可以通过附加有功功率信号调节有功参考值，维持直流电压稳定；换流站4工作于定交流电压工作方式，交流侧为无源负载供电。系统中各换流站的功率参考方向以注入直流网络为正方向。

VSC-MTDC系统中各换流站VSC结构相同，拓扑结构如图2所示［14］。

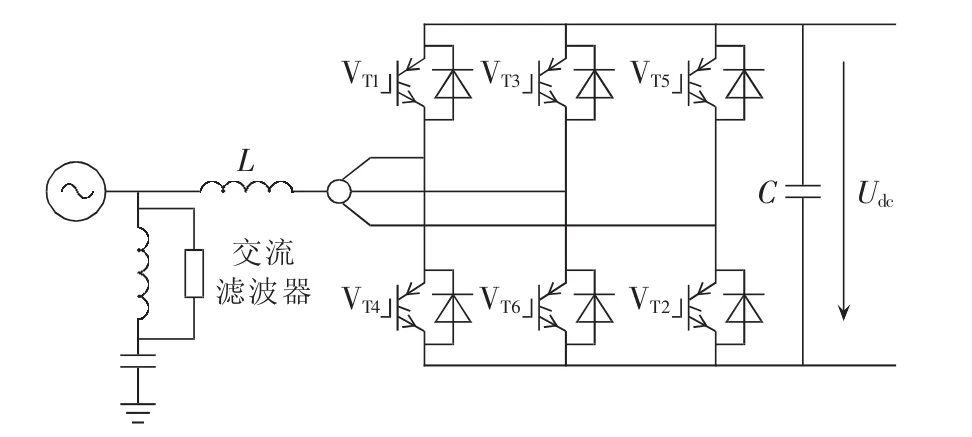
图2 VSC拓扑结构图Fig.2 Topology of VSC

在建立数学模型时，忽略交流滤波器和连接变压器的影响，将变压器的漏阻抗和损耗统一用换流电抗来表示，并在分析时假设三相主电路参数对称。

根据基尔霍夫电压定律可得交流侧微分方程在同步旋转dq坐标系下的表达式，采用d轴电网电压矢量定向后，得到简化后的数学模型为［15］：

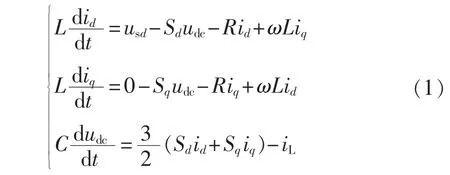
其中，ω为旋转角速度；Sd、Sq为同步坐标系下的开关函数；usd为电网电压d轴分量；id、iq分别为电网电流d、q轴分量；iL为直流线路电流；udc为换流站直流侧电压。

引入id、iq的前馈补偿进行解耦，得到两相同步旋转dq坐标系下的电压指令，电压指令经限幅和Park反变换后作为脉宽调制的指令信号，电压指令如下：

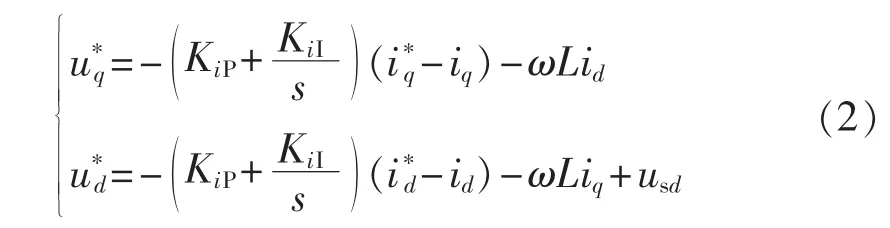
其中，KiP、KiI为电流 PI控制器参数。

电网电压定向后换流站吸收的有功和无功功率可以表示为：

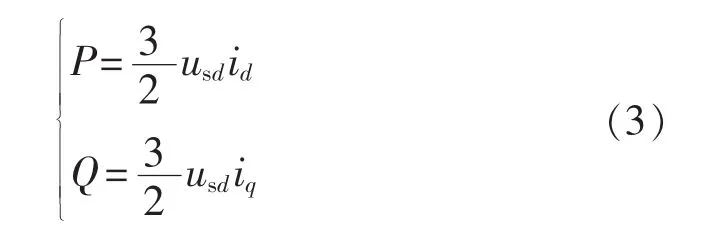
由上式可知，通过控制id、iq可以分别独立地控制换流站吸收的有功功率P和无功功率Q。

忽略换流站及连接电抗器损耗，则换流站交流侧与直流侧的功率守恒［16］，可得：

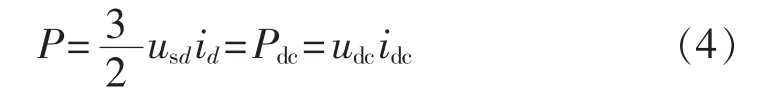
其中，idc为换流站直流侧电流。由式（4）可看出，通过控制电流id可维持换流站直流电压在一定范围内。

2 附加有功信号控制策略

2.1 直流电压分析

稳定运行时，忽略直流网络中的谐波分量，图1中VSC-MTDC系统直流网络电路如图3所示。

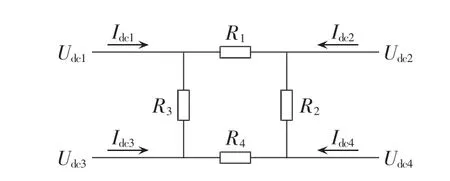
图3 MTDC系统直流网络电路Fig.3 DC net of MTDC system

为说明直流电压工作范围的计算方法，以下述稳定工作状态为例：换流站1工作于定直流电压模式；换流站2和3工作于整流状态，定有功功率模式；换流站4工作于定交流电压模式，为无源负载供电。取换流站流向直流网络为正方向。

由上述直流网络电路可得多端系统中各换流站直流电压之间关系为：

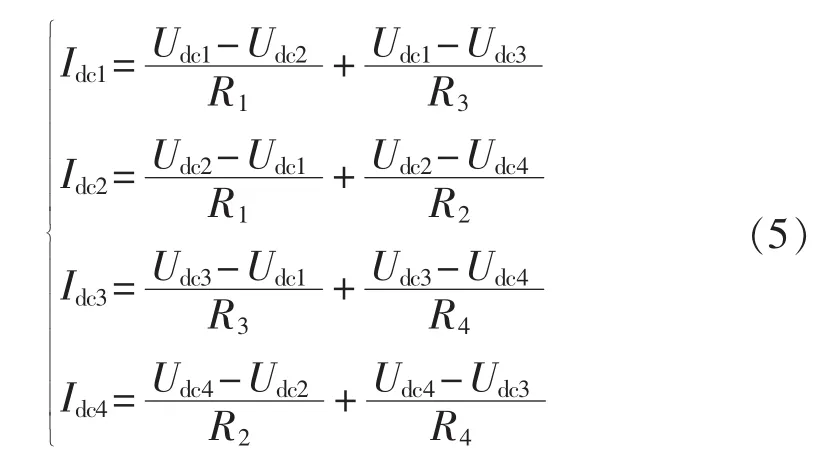
各换流站的功率可以表示为：

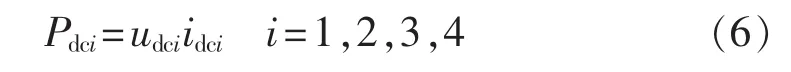
系统稳定运行时，换流站1处于定直流电压模式，未达到限流水平，直流电压参考值保持不变；换流站2和换流站3处于定有功功率模式，有功参考定值保持不变；换流站4交流侧所连负载功率不变。此时 Udc1、Pdc2、Pdc3、Pdc4为已知。

由换流站交直流两侧的功率守恒式（4）可得，换流站i传输有功功率的范围可以由iid来调节，而iid的范围又是由换流站控制器中的电流限制器来确定的，即 iid∈［iidmin，iidmax］，由此可得各个换流站的传输功率极限值［Pidmin，Pidmax］（i=1，2，3，4）。

由换流站直流电压表达式（5）、功率平衡表达式（6）及各换流站传输功率限值可得各个换流站的直流电压工作范围［Udcimin，Udcimax］，进一步结合各换流站功率限值可得直流电压的工作极限值［Udclim-，Udclim+］。同时还要考虑到换流站直流侧电容的耐压水平和线路电压过低时的过电流水平，直流电压基准值取1 kV时，换流站直流侧的电压值极限值的标幺值U*dclim应满足限制条件：0.8＜U*dclim＜1.2。

为防止由于测量及计算误差引起的控制策略不精确问题，直流电压计算时引入裕度值σ进行修正，电压修正形式如下：

其中，Uredcimin和Uredcimax为修正后直流电压工作范围；Udcmin和Udcmax为修正前计算得到的直流电压工作范围。

修正后的直流电压即在原有计算值基础上，电压上限值增加裕度值σ，电压下限值减去裕度值σ，从而使修正后得到的直流电压工作范围增大2σ，保证控制策略的精确性［17］，确保实际运行时的直流电压不会因误差等原因超出计算范围。

2.2 改进有功功率-直流电压特性曲线

当定直流电压站因故障退出运行或者进入限流模式时，向直流网络注入（或者吸收）的功率减小，导致直流网络有功功率不平衡，直流电压下降（或者上升），此时，处于定有功功率控制方式的换流站需要增加或者减小向直流网络的有功注入量。因此，可以基于直流电压的变化情况，调整故障期间定有功功率控制器的参考值，以保持故障期间直流网络的有功平衡。

为达到上述控制目标，本文中定有功功率控制器相应的改进有功功率-直流电压特性曲线如图4所示，右侧为处于整流状态时的情况，左侧为处于逆变状态下的特性曲线［18］。 图中，［Udcmin，Udcmax］为直流电压最大工作范围；［Udclim-，Udclim+］为直流电压的极限工作范围；Kr和Ki分别为整流和逆变时的可调曲线斜率。

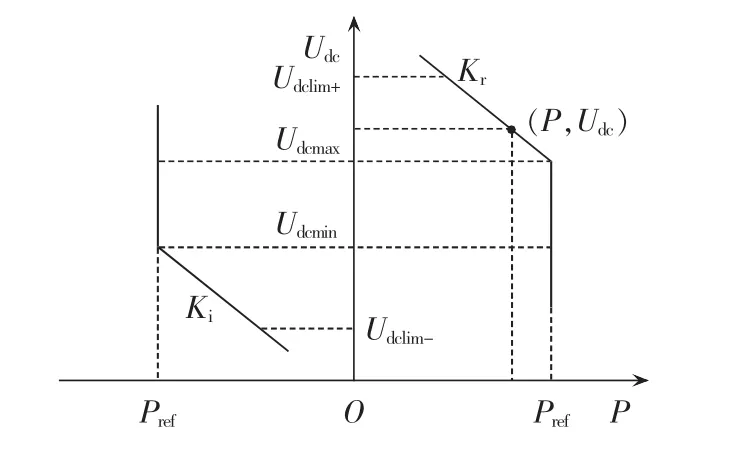
图4 改进有功功率-直流电压特性曲线Fig.4 Improved active power-DC voltage characteristic curves

2.3 基于附加有功信号的控制策略

2.3.1 附加有功功率信号计算

以定有功功率控制方式下的换流站处于整流状态为例说明附加有功功率信号的计算原理，即工作于图4中有功功率-直流电压特性曲线的右半部分。

正常情况下，直流电压处于［Udcmin，Udcmax］内，有功功率附加信号ΔPref=0，即换流站的有功功率给定值保持不变。此时，若处于定直流电压控制方式的换流站由于故障等原因失去对直流电压的控制时，直流电压迅速上升且超出直流电压最大工作范围的上限值，根据图4所示的改进特性曲线的线性部分，可得：

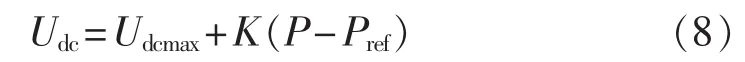
其中，K为初始电压下降系数；Pref为有功功率参考值。

假设有N个换流站采用上述改进的电压特性参与系统功率调节，直流网络出现不平衡功率ΔP时，对于第n个换流站，由于直流电压持续升高并超出Udcmax，令ΔPref=P-Pref，直流电压波动量与有功功率变化量之间关系为：

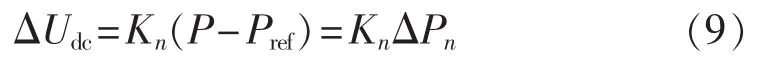
其中，Kn为第n个换流站对应的直流电压下降系数。

系统总的不平衡功率可以表示为：

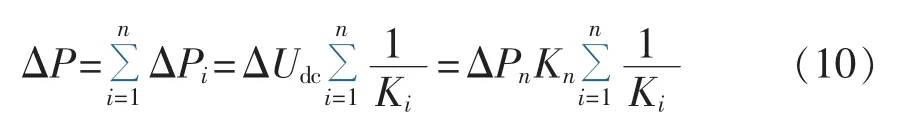
其中，Ki为第i个换流站的电压下降系数。

由式（10）可得，单个换流站承担的不平衡功率为：

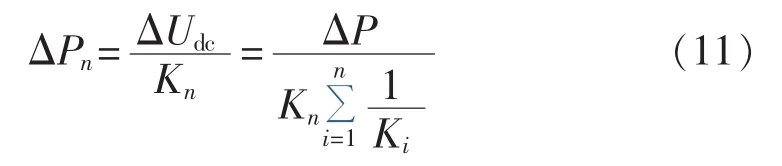
由上式可知，通过调整斜率K值的大小可以调节直流网络中的不平衡功率分配到相应换流站的多少。假设参与调节的换流站参数设置相同，则计算得到的附加有功功率信号相同，即分配的不平衡功率相同；各换流站参数不同时，较大的K值意味着分配到较少的不平衡功率，较小的K值意味着分配到较多的不平衡功率。

为避免采用附加有功功率信号的换流站在平衡直流网络功率时出现功率过载的情况，在计及换流站的可调容量裕度情况下调整斜率K，使有功功率裕度较大的换流站分担较多的不平衡功率，裕度较小的分担较少的不平衡功率。重新定义实际斜率使其在原有斜率基础上增加与可调功率裕度成反比的部分，调整如下：

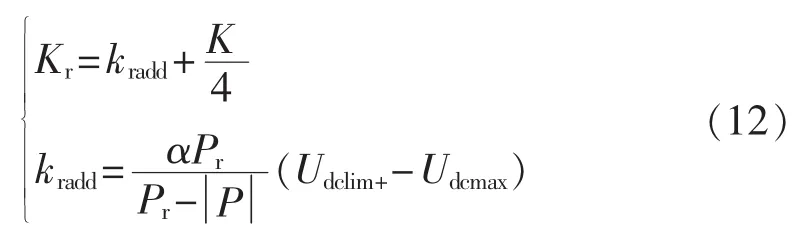
其中，Kr为换流站整流方式下的电压下降系数；Pr为换流站额定容量；α为斜率调整系数；为换流站可调功率裕度；kradd为电压下降系数附加部分。

调整后的直流电压斜率由两部分组成，一部分是原有斜率的1/4，保证调整后斜率值不至于过小，有利于控制器参数设置及系统的协调控制［19］；另一附加部分与相应换流站可调功率裕度成反比关系。

改进斜率后的曲线部分又有：

整理上式可得有功功率附加信号的计算公式可以表示为：

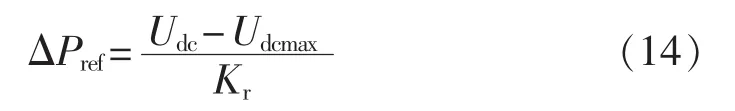
同理可得逆变状态下的有功功率附加信号计算公式为：

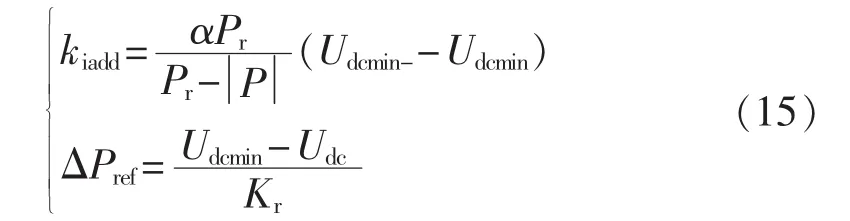
附加有功功率信号ΔPref的具体实现方法如图5所示。其中，Pdirection为定功率换流站的工作状态标志，Pref大于零时为整流状态，其值为1，反之逆变状态时为0。

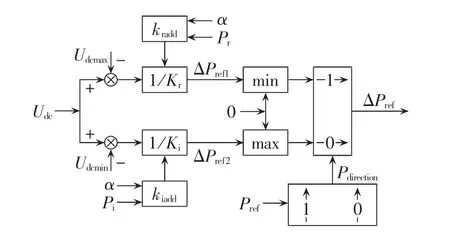
图5 有功功率附加信号计算框图Fig.5 Block diagram of additional active power signal calculation

附加有功功率信号的计算不需要换流站之间的通信，通过对本地换流站实时监测的变量Udc及常量Pr、Udcmin、Udcmax、Udclim计算得到有功功率的附加值，叠加到有功功率的给定值上，以实时地根据系统运行状况调整有功功率的输出，维持直流网络系统有功功率平衡及电压稳定。

2.3.2 附加有功功率控制器设计

系统中采用附加有功功率信号方法的换流站控制器的设计仍采用经典的前馈补偿、电流解耦的双环控制结构。VSC的内环结构为有功无功电流解耦的直接电流控制，外环控制根据换流站运行方式采用定有功功率控制［20］。

结合上述附加有功功率信号的计算及其参与有功调节的原理，外环有功功率控制器结构设计如图6所示。其中，ΔPref为计算得到的附加有功功率信号；idref、idmax、idmin分别为换流器交流侧输出电流有功分量参考值、最大值和最小值；Udclim为直流电压的极限工作范围。

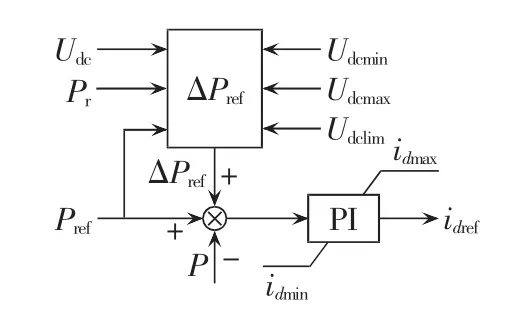
图6 外环有功功率控制器实现Fig.6 Design of outer-loop active power controller

附加有功信号的控制策略不需要换流站间的通信，减小了计算量，降低了建设成本及对快速通信的要求；相比于模式切换控制策略复杂的控制结构及切换信号的逻辑判断，不需要模式切换的特点简化了控制器的设计。

2.4 工作原理分析

2.4.1 正常运行状态

采用附加有功功率信号方法的换流站工作于整流状态时，有功功率控制器工作于改进直流电压特性曲线的右半部分，且满足：

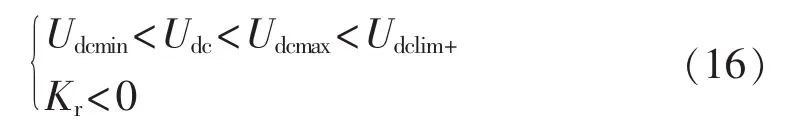
则附加有功功率信号为：

由图5中可得出，ΔPref与0作最小值比较，则输出为0，即正常运行时有功功率附加信号为0，不影响系统的正常运行。

同理，附加有功功率信号换流站工作于逆变状态时，正常条件下，有功功率控制器工作于改进直流电压特性曲线的左半部分，且满足：

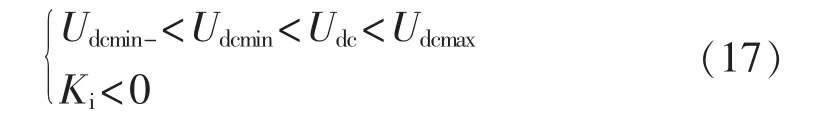
则附加有功信号为：

由图5中可得ΔPref与0作最大值比较，输出为0，即有功功率附加信号为0。

由以上分析可知，正常运行时，换流站2和3的有功功率给定值不会改变，保证了正常运行条件下有功功率的平衡和稳定。

2.4.2 扰动状态

状态1：换流站2工作于整流状态，定有功功率控制器工作于电压特性曲线右侧；换流站3工作于逆变状态，定有功功率控制器工作于电压特性曲线左侧，定直流电压站因故障退出运行后，由于交流母线电压下降，导致注入到直流网络的有功功率减少，直流电压下降后满足Udcmin-＜Udc＜Udcmin，则由有功功率附加信号计算式（16）、（17）可得，处于整流状态的换流站ΔPref=0，处于逆变状态的换流站ΔPref＞0，逆变站在其有功功率输出范围内参与调节有功功率不平衡量，维持直流电压恒定。同理可得，当主控站退出运行后直流网络电压上升时，处于逆变状态的换流站ΔPref=0，处于整流状态的换流站ΔPref＞0，参与有功功率的调节。

状态2：换流站2和换流站3均工作于整流状态，控制器运行于电压特性曲线右半部分。定直流电压站因故障退出运行后吸收有功功率减少，直流网络中有功功率过剩，直流电压Udc上升，当换流站直流电压满足 Udcmax＜Udc＜Udclim＋时，换流站 2和 3的直流电压下降系数根据式（12）进行修正后，经式（14）计算得到2个换流站承担的有功功率不平衡量ΔPref，ΔPref＜0且与各自换流站可调有功容量裕度成正比。同理可得，定直流电压站退出运行后直流电压下降时，换流站2和3承担的有功功率不平衡量ΔPref＞0且与各自换流站可调有功容量裕度成正比。考虑换流站可调有功容量裕度后的ΔPref可有效避免参与有功调节的换流站功率过载。

换流站2和3均工作于逆变状态时的工作原理和有功功率不平衡量的分配与状态2中的分析类似，故不再赘述。

3 仿真分析

为验证上述附加有功信号方法的有效性，在仿真软件平台PSCAD/EMTDC环境中搭建如图1所示的四端VSC-MTDC系统，并在3种故障情况下进行仿真验证，模型参数设置如下：交流系统电压为400 V，额定直流电压为1 kV，换流站1容量为25 kW，换流站2容量为20 kW，换流站3容量为20 kW，换流站4容量为20 kW，换流站1电流限值为［-31，31］A，换流站 2、换流站 3电流限值为［-41，41］A，线路参数为2 Ω、0.2 mH，初始直流电压下降系数为0.1，斜率调整系数α为0.02。

结合直流等效网络直流电压计算式（5）、（6）及给出的电流控制器限值，可得有功功率控制换流站2和3的直流电压工作范围为：

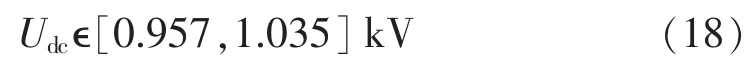
考虑到系统电压裕度，取电压裕度σ=0.02 kV，则本例中直流电压的正常工作范围为：

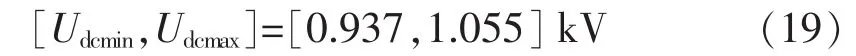
考虑到设备的电压安全限制和低电压过电流限制，直流电压极限值取为：

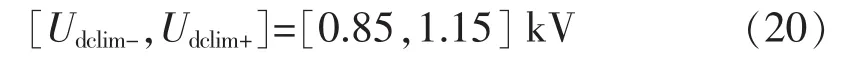
情形1：换流站2和3处于整流工作状态，有功功率给定定值分别为12 kW和8 kW，换流站4接入负载为10 kW，1 s时定直流电压站1交流侧发生三相接地短路情况，持续时间为0.15 s，仿真结果如图7所示。

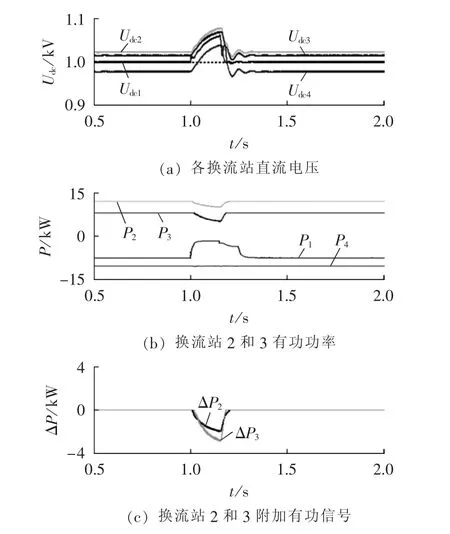
图7 情形1的仿真结果Fig.7 Simulative results of Case 1

由图7可知：故障前，系统处于稳定运行状态，有功功率平衡，定直流电压站始终维持直流电压在给定值1 kV，由于直流网络存在线路损耗，换流站2、3、4的直流电压值在1 kV左右的正常范围内；在1 s发生故障初期，定直流电压站短路接地后交流母线电压下降，导致定直流电压站从直流网络中吸收的有功功率减小，引起系统有功过剩、直流电压上升，当换流站2和3的直流电压分别在1.061 s和1.077 s达到各自直流电压工作上限值1.055 kV时，附加有功信号开始作用，叠加于有功功率控制器使换流站注入直流网络功率减小。由图7（c）可以看出，与换流站2相比，换流站3由于其可调有功容量较大，因此分担的功率不平衡量较多。直流电压在故障期间的最大值为1.072 kV，未超出电压极限值；1.15 s故障切除后，定直流电压站开始从直流网络中吸收功率，1.15～1.25 s为系统恢复阶段，作用于换流站2和3的附加有功信号上升为0，系统有功功率和直流电压恢复正常。

情形2：换流站2和3分别工作于整流和逆变状态，有功功率给定值分别为12 kW和-5 kW，其他系统设置同情形1，仿真结果如图8所示。

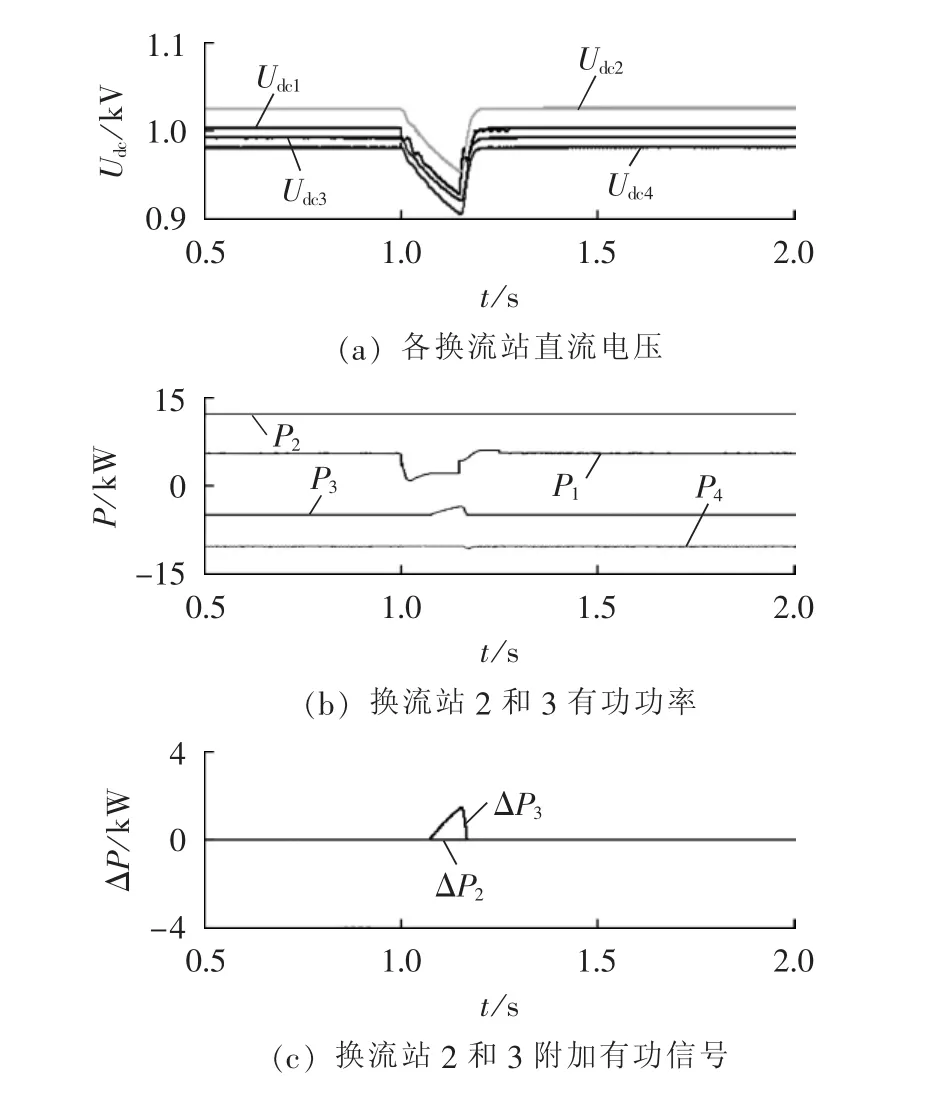
图8 情形2的仿真结果Fig.8 Simulative results of Case 2

由图8可知：故障前，系统有功功率平衡，主控站维持直流电压稳定；当1 s发生故障时，定直流电压站交流母线电压下降导致注入到直流网络中的有功功率减小，直流网络有功不足引起直流电压下降，当1.063 s换流站3的直流电压下降到工作范围的下限值0.937 kV，附加有功信号开始发挥作用，换流站3从直流网络中吸收的有功减小，但换流站2的直流电压下降到的最小值为0.953 kV，未达到电压下限值，因此，换流站2的附加有功信号为0，此时，直流网络有功增加，故障期间直流电压跌落到的最小值为0.911 kV，未超出电压极限范围，安全度过故障过程；1.15 s时刻故障清除后，由图8（b）可以看出附加有功信号迅速降为0，同时定直流电压站经过0.1 s的恢复过程开始向直流网络注入功率并恢复直流电压控制能力，各换流站功率和直流电压恢复故障前正常状态。

情形3：换流站2和3工作于整流工作状态，有功定值分别为12 kW和10 kW，为验证本文提出的控制策略在失去直流电压控制站之后，能够继续维持系统的直流电压，设置定直流电压站由于严重故障在1s时断开与交流电网的电气联系并且闭锁触发脉冲，1.5 s时换流站4所连负荷由15 kW减小为10 kW，系统其他参数设置同情形1，仿真结果如图9所示。

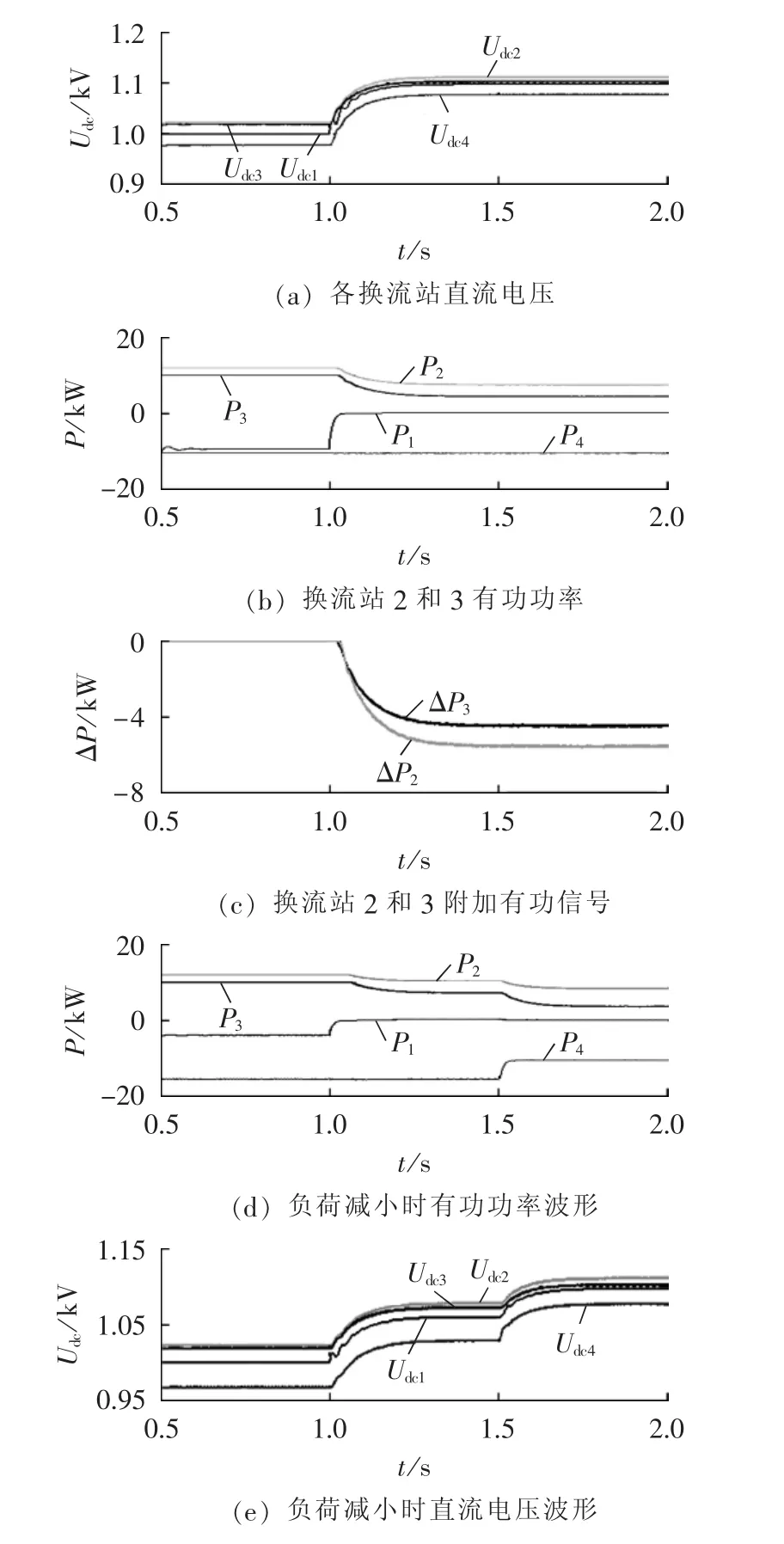
图9 情形3的仿真结果Fig.9 Simulative results of Case 3

由图9可知：故障前系统的运行状态与前述分析相同；1 s发生严重故障时，定直流电压站从直流网络中吸收的有功功率迅速降为0，直流网络中有功功率过剩，直流电压迅速上升，上升到换流站工作电压上限时，换流站2和3分别在1.071 s和1.082 s引入附加有功信号，减少有功功率注入量。由图9（c）可以看出，可调有功裕度较大的换流站3分担较多的有功不平衡量，使输出有功功率下降以维持系统功率平衡。同时，附加有功不平衡度和直流电压上升速度减缓，最终稳定在1.085 kV附近，未超出系统的极限运行电压。由此可见，附加有功信号控制策略可以在定直流电压站停运情况下，维持系统有功平衡，保证直流电压在极限范围以内和非故障设备的持续运行。

由图9中换流站4在1.5 s减负荷时的波形图（d）和（e）可以看出，在失去直流电压控制站后，当系统中再次出现有功功率不平衡扰动时，直流电压仍可以被控制在安全运行范围内。这是因为由式（5）、（6）及有功功率-直流电压特性可以看出，有功功率和直流电压关系密切，有功功率的平衡可以间接地反映直流电压的稳定，当出现功率扰动时，附加有功信号作用使定有功功率换流站通过实时地调整其功率输出维持直流电压的稳定。仿真结果表明，当失去直流电压控制站时，附加有功信号策略可以在一定范围内维持直流电压的稳定。

4 结论

本文提出一种基于附加有功功率信号的VSCMTDC系统平衡控制策略，通过在定有功功率换流站引入基于可调有功容量裕度的附加有功功率信号，实现定直流电压站故障期间功率分配和直流电压控制，增强VSC-MTDC系统在故障期间的稳定运行能力。

所提控制策略不需要站间通信和模式切换且易于实现，考虑换流站可调容量裕度条件下可有效防止参与有功功率调节的换流站过载。定有功功率换流站在定直流电压站故障时检测本地直流电压，依据改进有功功率-直流电压特性按照各换流站的可调有功功率裕度分配不平衡功率，计算得到附加有功功率信号并叠加到定功率控制器功率设定值中，有效解决了定直流电压站故障时系统功率不平衡及直流电压失稳问题。仿真结果验证了所提方法在扰动期间维持有功功率平衡和直流电压稳定的有效性。

［1］文安，邓旭，魏承志，等.柔性直流输电系统交直流并列运行与孤岛运行方式间的切换控制［J］.电力自动化设备，2014，34（7）：99-106.WEN An，DENG Xu，WEIChengzhi，etal.Switchingcontrol between AC-DC parallel and islanded operations of VSC-HVDC transmission system［J］.Electric Power Automation Equipment，2014，34（7）：99-106.

［2］COLE S，BEERTEN J，BELMANS R.Generalized dynamic VSC MTDC model for power system stability studies［J］.IEEE Transactions on Power Systems，2010，25（3）：1655-1662.

［3］廖勇，王国栋.双馈风电场柔性高压直流接入下的网侧变换器改进 Backstepping 控制策略［J］.电力自动化设备，2014，34（2）：35-41，47.LIAO Yong，WANG Guodong.Improved Backsteppingcontrol strategy for GSVSC of DFIG wind farm with VSC-HVDC gridintegration［J］.Electric Power Automation Equipment，2014，34（2）：35-41，47.

［4］赵成勇，孙营，李广凯.双馈入直流输电系统中VSC-HVDC的控制策略［J］.中国电机工程学报，2008，28（7）：97-103.ZHAO Chengyong，SUN Ying，LI Guangkai.Control strategy of VSC-HVDC in dual-infeed HVDC system［J］.Proceedings of the CSEE，2008，28（7）：97-103.

［5］姚伟，程时杰，文劲宇.直流输电技术在海上风电场并网中的应用［J］.中国电力，2007，40（10）：70-74.YAO Wei，CHENG Shijie，WEN Jinyu.ApplicationofHVDC technology in grid integration of offshore wind farms［J］.Electric Power，2007，40（10）：70-74.

［6］LU W X，OOI B T.DC overvoltage control during loss of converter in Multi-terminal Voltage-Source Converter-based HVDC（M-VSC-HVDC）［J］.IEEE Transactions on Power Delivery，2003，18（3）：915-920.

［7］VASQUEZ J C，GUERRERO J M，LUNA A，et al.Adaptive droop controlapplied tovoltage-source invertersoperatingin gridconnected and islanded modes［J］.IEEE Transactions on Industrial Electronics，2009，56（10）：4088-4096.

［8］陈谦，唐国庆，潘诗锋.采用多点直流电压控制方式的VSC多端直流输电系统［J］.电力自动化设备，2004，24（5）：10-15.CHEN Qian，TANG Guoqing，PAN Shifeng.VSC-MTDC using multiterminal DC voltage control scheme［J］.Electric Power Automation Equipment，2004，24（5）：10-15.

［9］陈海荣，徐政.适用于VSC-MTDC系统的直流电压控制策略［J］.电力系统自动化，2006，30（19）：28-33.CHEN Hairong，XU Zheng.A novel DC voltage control strategy for VSC based multi-terminal HVDC system［J］.Automation of Electric Power Systems，2006，30（19）：28-33.

［10］吴俊宏，艾芊.多端柔性直流输电系统在风电场中的应用［J］.电网技术，2009，33（4）：22-27.WU Junhong，AI Qian.Research on multiterminal VSC-HVDC system for wind-farms［J］.Power System Technology，2009，33（4）：22-27.

［11］赵成勇，胡东良，李广凯，等.多端VSC-HVDC用于风电场联网时的控制策略［J］.电网技术，2009，33（17）：135-140.ZHAO Chengyong，HU Dongliang，LI Guangkai，et al.Control strategy for integration of wind farms by multi-terminal VSCHVDC［J］.Power System Technology，2009，33（17）：135-140.

［12］阮思烨，李国杰，孙元章.多端电压源型直流输电系统的控制策略［J］.电力系统自动化，2009，33（12）：57-60，96.RUAN Siye，LI Guojie，SUN Yuanzhang.A control stratey for multi-infeed VSC-HVDC systems［J］.Automation of Electric Power Systems，2009，33（12）：57-60，96.

［13］任敬国，李可军，刘合金，等.基于改进定有功功率控制特性的VSC-MTDC 系统仿真［J］.电力系统自动化，2013，37（15）：133-139.REN Jingguo，LI Kejun，LIU Hejin，et al.Coordinated control strategy of VSC-MTDC system based on improved DC voltageactive power characteristic［J］.Automation of Electric Power Systems，2013，37（15）：133-139.

［14］任敬国，李可军，牛林，等.基于附加信号的VSC-HVDC系统改进有功功率控制策略［J］.电力自动化设备，2013，33（7）：46-51.REN Jingguo，LI Kejun，NIU Lin，et al.Advanced active power controlstrategy based on additionalsignalforVSC-HVDC transmission system［J］.Electric Power Automation Equipment，2013，33（7）：46-51.

［15］梁海峰，李庚银，周明，等.电压源换流器高压直流输电的动态等效电路及其特性分析［J］.中国电机工程学报，2010，30（13）：53-60.LIANG Haifeng，LI Gengyin，ZHOU Ming，et al.Dynamic equiva-lent circuit of VSC-HVDC and its performance analysis［J］.Proceedings of the CSEE，2010，30（13）：53-60.

［16］袁旭峰，文劲宇，程时杰.多端直流输电系统中的直流功率调制技术［J］.电网技术，2007，31（14）：57-61.YUAN Xufeng，WEN Jinyu，CHENG Shijie.DC power modulation in multi-terminal HVDC transmission system［J］.Power System Technology，2007，31（14）：57-61.

［17］胡兆庆，毛承雄，陆继明，等.一种新型的直流输电技术——HVDC Light［J］.电工技术学报，2005，20（7）：12-16.HU Zhaoqing，MAO Chengxiong，LU Jiming，et al.New high voltage direct current transmisson technology-HVDC Light［J］.Transactions on China Electrotechnical Society，2005，20 （7）：12-16.

［18］喻锋，王西田，解大.多端柔性直流下垂控制的功率参考值修正方法［J］.电力自动化设备，2015，35（11）：117-122.YU Feng，WANG Xitian，XIE Da.Power reference correction method for droop control of VSC-MTDC system［J］.Electric Power Automation Equipment，2015，35（11）：117-122.

［19］FLOURENTZOU N，AGELIDIS V G，DEMETRIADES G D.VSC-based HVDC power transmission systems：an overview［J］.IEEE Transactions on Power Electronics，2009，24（3）：592-602.

［20］陈实，朱瑞可，李兴源，等.基于VSC-MTDC的风电场并网控制策略研究［J］.四川大学学报：工程科学版，2014，46（2）：147-152.CHEN Shi，ZHU Ruike，LI Xingyuan，et al.Research on control strategy for interconnection of wind farms by VSC-MTDC ［J］.Journal of Sichuan University：Engineering Science Edition，2014，46（2）：147-152.