基于引力模型的电动汽车充电站选址规划

程宏波, 肖永乐, 王 勋, 伦 利, 李明慧

(华东交通大学电气与电子工程学院， 江西 南昌 330013)

基于引力模型的电动汽车充电站选址规划

程宏波, 肖永乐, 王 勋, 伦 利, 李明慧

(华东交通大学电气与电子工程学院， 江西 南昌 330013)

作为电动汽车的配套设施，充电站的收益与服务的电动汽车的数量及其充电次数有关，而电动汽车的数量及充电次数会受到充电站使用便捷性的影响。为了解决此问题，本文分析了充电站等级、电动汽车规模以及距离之间的相互影响关系，得到了充电站与电动汽车之间的相互吸引模型，在考虑相互影响的基础上，得到电动汽车数量发展的引力模型函数；定义充电便捷性函数，得到了充电次数和便捷性之间的引力关系，在此基础上得到考虑未来发展的电动汽车充电站规划模型。最后，采用微分进化算法对建立的模型进行求解，针对某一具体算例进行了仿真分析，结果表明，本文选址规划符合实际，为充电站的选址规划提供了参考。

引力模型； 电动汽车充电站； 选址规划； 充电次数； 便捷性

1 引言

作为电动汽车重要的配套设施，充电站的规划建设会对电动汽车的推广产生重大影响，规划合理、使用便捷的充电站将会对电动汽车的大规模应用产生有力的推动作用。

作为重要的商业设施，充电站的建设需要考虑经济收益[1-3]。充电站的经济收益主要通过向电动汽车售电获取，因而，经济收益的多少和充电站所服务的电动汽车数量及充电频率有关，充电站服务的电动汽车数量越多，电动汽车充电的次数越高，充电站所能获取的收益就越多。

当前，充电站的规划多是在满足电网约束条件[4-6]、交通约束[7,8]和用户使用需求[9-11]的情况下，从运营成本最低的角度考虑[12,13]，忽略了充电站的商业属性，不利于激发充电站建设的积极性。

部分文献从收益的角度出发，对充电站建成后未来可能获得的经济收益[14,15]和社会收益[3,10]进行分析。文献[14]从充电站运营情况出发，根据电网分时电价制定相应控制措施，使得充电站的收益最大；文献[15]对有序和无序充电两种情况进行了比较，证明了在有序充电的情况下其收益更大；文献[3,10]则分别考虑了充电站能够降低规划区域内的碳排放量，对由此增加的低碳收益进行了分析。但无论是在分析经济收益还是分析社会收益时，这些方法多将未来服务的电动汽车的数量视为固定不变的常数，每年提供的电能也多用固定容量代替，这与电动汽车发展的实际情况不相符合。实际中，某一地区的电动汽车数量多是发展变化的，它受国家政策、配套充电设施建设情况等因素的影响。作为配套设施的充电站建设越多，使用越方便，公众购买电动汽车的积极性就越高，电动汽车数量的增长就会越快；电动汽车充电越便捷，用户使用电动汽车的愿望就越强烈，使用频率也就越频繁，到充电站充电的次数就会越多。电动汽车的数量越多，总的充电次数就会越多，充电站的收益将会越大。

因而，充电站的规划结果和影响因素之间存在着相互影响、相互关联的关系，在对充电站进行规划时，需要对这种关联关系加以考虑。

为准确计算出充电站的收益，本文将引力模型引入到充电站的规划建设中，利用引力定律分别建立了电动汽车数量和充电次数的引力发展模型。首先，分析了充电站对用户购买电动汽车的影响，建立了充电站的等级、距离和电动汽车数量的引力模型；其次，建立了充电站便捷系数和用户充电次数关系模型；在计算充电站收益时，考虑增加的电动汽车，使得充电站预测收益更加符合实际；最后使用微分进化算法对该模型进行求解。

2 引力模型

根据万有引力定律，任意两个质点之间引力的大小与其质量成正比，与距离的平方成反比。而在物体质点内部，引力不变。万有引力拓展式为：

(1)

式中，G为引力常数；m1、m2为两质点的质量；R为两质点之间的距离；RE为任意一质点的圆内半径；F0为圆内半径引力的大小。

引力定律作为一种通用规律，可用于描述相互作用的多个因素之间的关联关系，在道路规划[16]、居住点优化[17]和开发区的规划建设[18]中得到了应用。

电动汽车充电站和用户之间存在着相互的吸引和促进，充电站等级越高，区域内电动汽车数量越多，两者的相互吸引作用越强，电动汽车到充电站充电越方便，用户购买电动汽车的欲望就越强，电动汽车的数量增长速度也就越快；同理，两者的相互吸引越强，电动汽车充电越便捷，用户使用就越多，到充电站充电的次数就会增加越多。

因此，在对充电站进行规划建设时，需要考虑充电站和电动汽车之间的相互吸引和影响。而作为两个相互作用的对象，充电站和电动汽车之间的相互吸引作用与自然界通用的万有引力模型相似，充电站为相互作用的一方，其等级和规模等效于作用一方的质量；电动汽车为相互作用的另一方，其数量起到的作用与引力中的质量相似。因而，万有引力模型可用来表示两者间的相互作用关系，较适合用来反映相互联系对电动汽车数量及充电次数的影响。

3 考虑引力影响的电动汽车数量

充电站和用户是相互作用的两个对象，充电站对用户产生吸引作用，充电站建设等级越高，电动汽车充电就会越方便快捷，对未购买电动汽车的用户能够起到较好的宣传示范作用。区域内电动汽车的数量越多，示范作用越明显，对其他用户购买电动汽车的促进作用越强，电动汽车的数量增加越多。充电站建设在离用户较近的区域，能够刺激用户购买电动汽车。

根据以上分析，充电站对用户吸引系数Ii为：

(2)

式中，K1ig为等级为g的充电站的引力常数，它与充电站的圆内半径、充电站的建设等级以及用户最大同时充电率Smax有关；r为用户到充电站的距离；Rig为充电站的圆内半径，与充电站服务的最大半径Rmax、充电站服务的汽车数量Pi和充电站的建设等级Gig相关；α为充电站对用户购买电动汽车的吸引常数。

充电站的圆内半径为：

(3)

充电站的引力常数为：

(4)

由式(2)可知，当用户在充电站影响的圆内半径之外时，充电站建设等级越高，电动汽车数量越多，距离用户越近，则对用户的吸引系数就会越大；随着充电站和用户之间距离的增大，其对用户的吸引力度逐渐较小。由引力模型在经济领域的应用可知，充电站的圆内服务半径与充电站的最大服务半径、电动汽车数量和建设等级相关。在万有引力模型中，在圆内和表面产生的引力相等，本文中的引力常数由充电站的圆内半径、建设等级和电动汽车最大同时充电率决定。充电站的规划应尽可能增大对用户的整体吸引系数，从而对电动汽车用户数量的增长起到促进作用，实现充电站和电动汽车的双向良性循环。

考虑电动汽车发展的自然增长速度β，以及充电站建设对电动汽车发展的促进作用，某区域内电动汽车数量的增长规律可表示如下：

Pli=Pi(β+Ii)l

(5)

式中，Pli为第i座充电站第l年服务的电动汽车的数量；Pi为规划充电站i服务的汽车数量；β为电动汽车的自然增长速度。

充电站对电动汽车用户的引力关系如图1所示，图1(a)表示充电站对不同距离用户的吸引系数，图1(b)表示与图1(a)对应吸引系数下用户购买电动汽车的等购买概率线，颜色深浅表示吸引系数的大小和充电次数的多少。以充电站建设位置为圆心，实线表示充电站影响的圆内半径，在图1(a)的实线圆内，颜色较深，充电站对用户吸引系数较大，所对应的图1(b)中用户希望购买电动汽车的欲望强烈，用户购买电动汽车的概率较高，电动汽车增长的数量也会加快，而且在该区域内，充电站对用户的吸引系数相差不大。实心圆外，随着距离的逐渐增大，颜色逐渐变淡，充电站对用户的吸引力逐渐减小，所对应的图1(b)中用户的购买概率逐渐降低，电动汽车增加的数量相应减少。

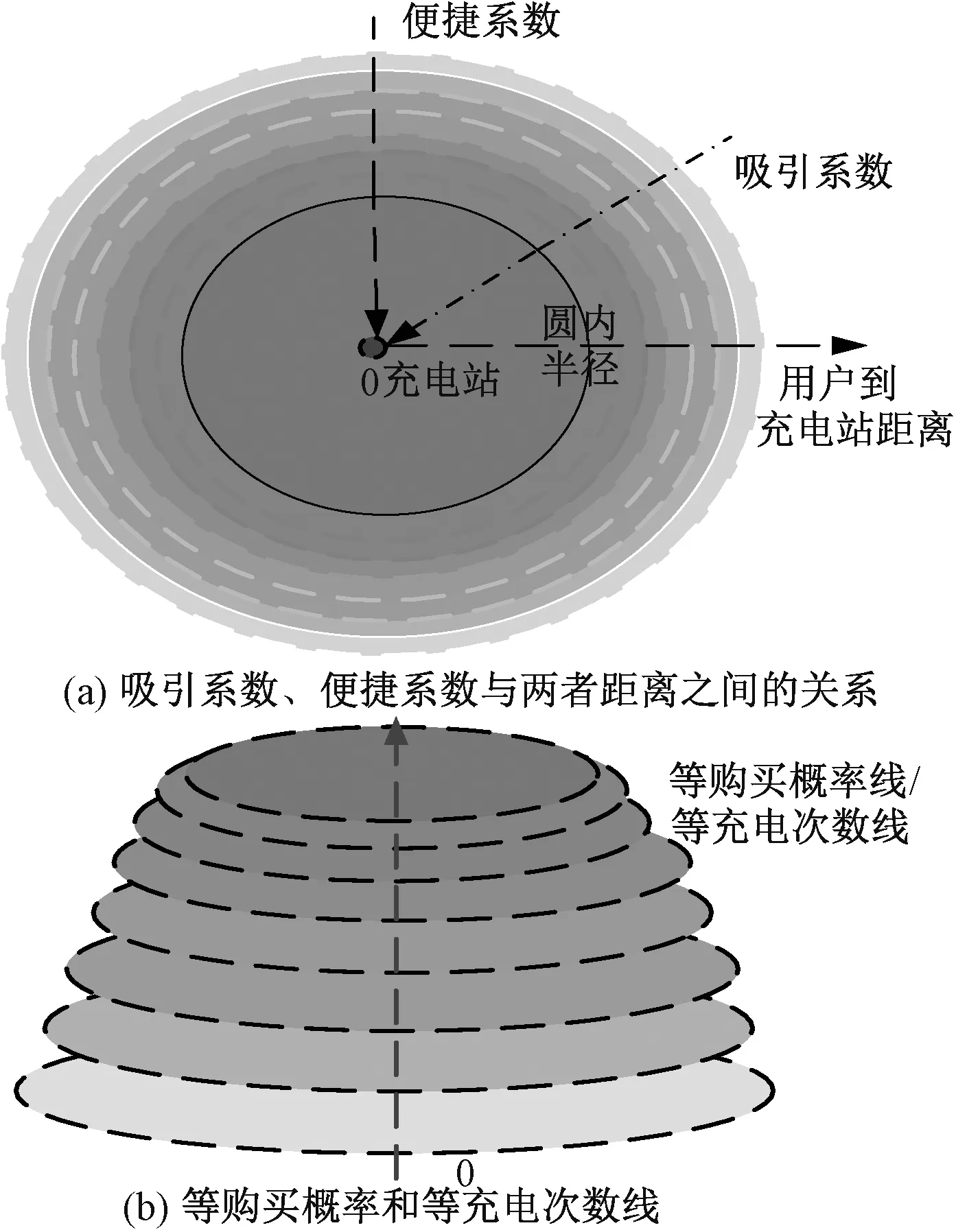
图1 充电站和用户的引力模型关系图Fig.1 Relation between charging station and users

4 考虑引力影响的电动汽车充电次数

充电站建成之后，用户使用电动汽车的积极性与充电站的使用便捷性直接相关。充电站建设等级越高，服务能力越强，充电等待时间越短，充电就越便捷；同样，电动汽车离充电站越近，到充电站充电就越方便便捷。当充电便捷时，用户使用电动汽车的积极性就越高，相应的电动汽车充电次数就会越多。充电站和用户充电次数之间的这种相互影响可以用便捷系数Big表示为：

(6)

式中，K2ig为常数系数，其与充电站的圆内半径、用户的便捷常数B0、建设等级和最大同时充电率有关；U为任意电动汽车用户。

(7)

用户充电次数和便捷系数成正比，用户的便捷系数越高，其到充电站充电就会越方便快捷，使用电动汽车越频繁，则到充电站充电的次数越高；反之，则减少了电动汽车的使用频率，进而减少了充电次数；距离充电站最远的用户，虽然便捷系数较低，日常使用电动汽车用户的频率较低，但其出行还是需要一定的充电次数。设充电次数最小值ρ，由此建立用户到充电站i的充电次数fi的发展规律：

fi=ρ(1+Big)

(8)

用户的充电次数和充电站的引力关系如图1所示，图1(a)表示不同距离的用户到充电站充电的便捷系数，图1(b)表示与图1(a)对应便捷系数下用户的等充电次数线，颜色深浅表示用户的便捷系数的高低和充电次数的多少。在图1(a)的实线圆内，颜色较深，用户便捷系数较大，所对应的图1(b)中用户到充电站方便快捷，增加了用户使用电动汽车的频率，从而增加了用户到充电站的充电次数。实心圆外，随着用户到充电站距离的增加，颜色逐渐变淡，用户使用充电站的便捷系数降低，所对应的图1(b)用户的充电次数逐渐减少。

5 收益最大化的电动汽车充电站选址规划

充电站收益来源是向用户提供电能并获取充电费用。考虑到电动汽车发展的情况，在计算充电站收益时，不仅要考虑规划时充电需求的情况，还要考虑充电站建设后对电动汽车发展可能造成的影响。

考虑电动汽车数量发展的收益规划模型为：

(9)

式中

(10)

(11)

(12)

Cl为规划l年充电站的年均收益；Pli为规划l年充电站i的电动汽车数量；pc为电动汽车充电站充电电价；pw为电网电价；Q为用户每次充电电量；Cc为充电站的年均建设成本；τ为充电站的年收益率；T为充电站的运行年限；Clr为规划l年的充电站平均年运行成本；Cls为规划l年用户到充电站的损耗费用；n为规划建设充电站的数量；CAi为单位征地价格；Ai为充电站的征地面积；CBi为充电站购买基础设备成本；μ为线路损耗与工人工资比例系数；γ为电动汽车行驶每公里所需费用；ri为用户到充电站i的距离。

6 实例验证

以某区域的电动汽车选址规划为例，验证本文方法的可行性和有效性。该区域为面积(16×16)km2的矩形，内含不同类型的地段，按城市征地性质不同，把这些小区划分为工业区、居民区和商业区三种，三者之间征地成本不同。电动汽车在70个相对集中的聚点内，每个聚点内的电动汽车数量在15～200之间，聚点位置如图2所示。

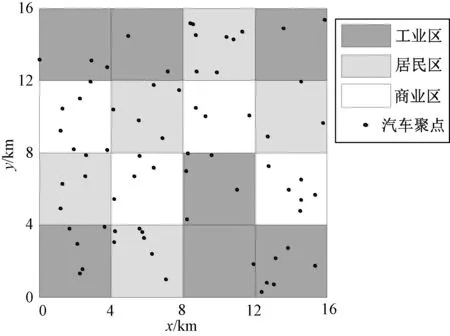
图2 电动汽车聚集点的分布情况Fig.2 Distribution of EV rallying point

参数选取如下：工业区、用户区和商业区的征地价格分别为0.07万元/m2、0.21万元/m2和0.68万元/m2，不同等级的充电站建设规模参考北京市出台的充电站建设标准。取最大同时充电率Smax=0.03，为满足最大同时充电率的电动汽车数量要求，n>3。设充电站运行20年，年回收率为0.10，充电量以比亚迪E6为例，取40 kW·h，电网电价为0.6元/(kW·h)，充电站的电价为1元/(kW·h)，充电次数阈值fe=100，充电站的建设应满足未来两年充电服务需求，考虑到电动汽车增长量，两年后的充电站最小建设数量为6座。

对建立的模型使用微分进化算法进行求解，在规划区域内随机产生充电站的坐标，得到坐标处的收益；然后通过交叉和变异步骤，得到不同位置的收益；最后通过选择得到收益最大化的充电站选址规划位置。

算法参数如下：选取种群规模为500，迭代次数800，交叉因子0.5，比例因子0.8，对每个n值运算20次。

图3为考虑收益最大时充电站的规划建设选址方案，可以看出，充电站的选址主要在电动汽车聚集点比较集中的区域和征地价格比较便宜的工业区和用户区。由于商业区的单位征地价格比较昂贵，平均分摊到运行年份内的费用较高，使得在该区域建设充电站的相对费用较高，而增加的电动汽车数量、充电次数不能补偿均摊的征地费用。

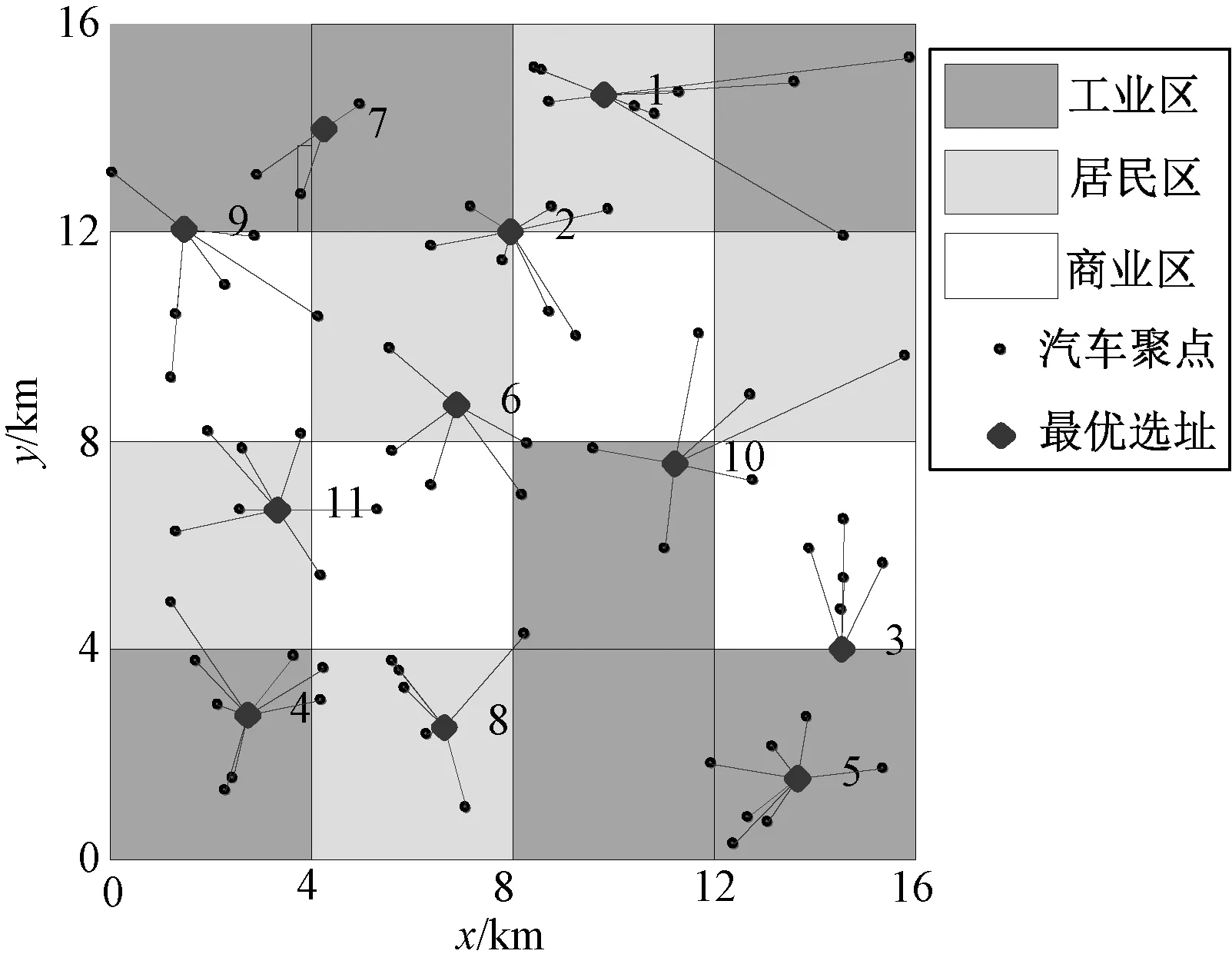
图3 充电站最优选址Fig.3 Optional planning of charging station

图4为采用本文方法时求得的充电站收益与文献[1]方法的对比，虚线所示为根据本文方法得到的收益最大的规划方案。可以看出，本文规划方法求得的收益逐年递增，而一般规划模型中，由于电动汽车数量和充电次数被视为固定不变，其不同年份的收益固定不变；本文模型中规划充电站收益先增加，后减少，反应了规划结果对电动汽车的影响作用，充电站的规划建设促进了电动汽车数量以及使用频率的增加，使得充电站的收益相应增加，但随着充电站数量的进一步增加，充电收益的增加速度小于建设成本增长的速度，故充电站的收益又逐渐降低；规划当年的收益要比一般规划算法求解的结果少，主要是由于考虑为电动汽车发展提供充电需要，建设初期的投资成本较高。

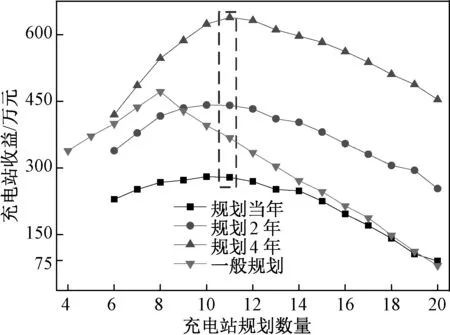
图4 充电站收益的对比Fig.4 Income comparison of EV charging station

由图4可以看出，本例中规划建设11座充电站的收益最大，采用引力模型的充电站规划结果，其服务能力随着时间的发展而增加，规划结果能满足未来电动汽车动态发展的需求，减少了因电动汽车增长而对充电站进行改、扩建的费用，总体收益更高。

表1列出了采用本文引力模型与文献[1]中一般模型进行规划后的充电站服务能力与收益的对比。其中电动汽车实际数量是按某区域2013年和2014年电动汽车年增长率分别为9.5%和10.5%计算得到。可以看出，采用一般模型进行求解，规划结果可在短期内满足电动汽车充电的需求，但考虑充电站对电动汽车发展的促进作用，在规划后2年和4年时将无法满足电动汽车的实际充电需求，此时需扩建2座充电站，导致当年的成本增加，收益降低。因而，本文引力模型所得的规划结果可满足未来特定时间内的实际需求。

表1 电动汽车发展数量表Tab.1 Numbers of electric vehicles increase

7 结论

本文建立了基于引力模型的充电站选址规划，以收益最大化为目标函数，动态考虑了用户充电次数模型，根据引力模型分析了充电站建设位置、等级和距离对用户购买电动汽车吸引力以及用户充电次数的影响。充电站规划建设不仅要满足当前电动汽车充电需求，还应该为未来电动汽车的增长预留空间。本文建立了充电站与用户的引力模型，分析充电站对用户影响下电动汽车增长数量。此外，把充电站的建设成本、运行成本以及用户到充电站的费用考虑到充电站规划之中。通过求解该模型，得出了以下结论。

(1)根据引力模型，得到充电站影响下电动汽车的增长数量，充电站规划时间相对较长时，年收益较多，这些为电动汽车的推广提供了参考。

(2)得到用户到充电站充电次数与用户便捷性的关系，更符合实际用户使用充电站的情况，准确得到充电站的收益。

[1] 宋志成, 王勋, 伦利, 等 (Song Zhicheng, Wang Xun, Lun Li, et al.). 基于收益最大化的电动汽车充电站选址规划 (Site planning of EV charging stations based on the maximum profits) [J]. 华东交通大学学报 (Journal of East China Jiaotong University), 2014,31 (1):50-55.

[2] 唐现刚, 刘俊勇, 刘友波, 等 (Tang Xiangang, Liu Junyong, Liu Youbo, et al.). 基于计算几何方法的电动汽车充电站规划(Electric vehicle charging station planning based on computational geometry method) [J]. 电力系统自动化 (Automation of Electric Power Systems), 2012, 36(8): 24-30.

[3] 宋志成 (Song Zhicheng). 基于收益最大化的电动汽车充电站选址规划 (Site planning of EV charging stations based on the maximum profits) [D]. 南昌: 华东交通大学 (Nanchang: East China Jiaotong University), 2014.

[4] 陈婷, 卫志农, 吴霜, 等 (Chen Ting, Wei Zhinong, Wu Shuang, et al.). 考虑电动汽车充电站选址定容的配电网规划 (Distribution network planning by considering siting and sizing of electric vehicle charging stations) [J]. 电力系统及其自动化学报 (Proceedings of the CSU-EPSA), 2013, 25 (3): 1-7.

[5] 所丽, 唐巍, 白牧可, 等 (Suo Li, Tang Wei, Bai Muke, et al.). 考虑削峰填谷的配电网集中型充电站选址定容规划 (Locating and sizing of centralized charging stations in distribution network considering load shifting) [J]. 中国电机工程学报(Proceedings of the CESS), 2014, 34 (7): 1052-1060.

[6] 葛少云, 冯亮, 刘洪, 等 (Ge Shaoyun, Feng Liang, Liu Hong, et al.). 考虑车流信息与配电网络容量约束的充电站规划 (Planning of charging stations considering traffic flow and capacity constraints of distribution network) [J].电网技术 (Power System Technology), 2013, 37(3): 582-589.

[7] 严弈遥, 罗禹贡, 朱陶, 等 (Yan Yiyao, Luo Yugong, Zhu Tao, et al.). 融合电网和交通网信息的电动车辆最优充电路径推荐策略 (Optimal charging route recommendation method based on transportation and distribution information) [J].中国电机工程学报(Proceedings of the CESS), 2015, 35(2): 310-318.

[8] 葛少云, 冯亮, 刘洪, 等 (Ge Shaoyun, Feng Liang, Liu Hong, et al.). 考虑电量分布及行驶里程的高速公路充电站规划 (Planning of charging stations on highway considering power distribution and driving mileage) [J]. 电力自动化设备 (Electric Power Automation Equipment), 2013, 33(7): 111-116.

[9] 葛少云, 冯亮, 刘洪, 等 (Ge Shaoyun, Feng Liang, Liu Hong, et al.). 考虑用户便捷性的电动汽车充电站规划(Planning of electric vehicle charging stations considering users’ convenience) [J]. 电工电能新技术 (Advanced Technology of Electrical Engineering and Energy), 2014, 33(2): 70-75.

[10] 陈光, 毛召磊, 李济沅, 等 (Chen Guang, Mao Zhaolei, Li Jiyuan, et al.). 计及碳排放的电动汽车充电站多目标规划 (Key technologies of using renewable energy to capture carbon from ambient air directly) [J]. 电力系统自动化 (Automation of Electric Power Systems), 2014, 38(17): 49-53, 136.

[11] 张国亮, 李波, 王运发 (Zhang Guoliang, Li Bo, Wang Yunfa). 多等级电动汽车充电站的选址与算法 (Location and algorithm of multi-level electric vehicle charging stations) [J]. 山东大学学报 (工学版) (Journal of Shandong University (Engineering Science)), 2011, 41 (6): 136-142.

[12] Long Jia, Zechun Hu, Yonghua Song, et al. Optional siting and sizing of electric vehicle charging stations [A]. 2012 IEEE International Electric Vehicle Conference (IEVC)[C]. 2012. 1-6.

[13] 任玉珑, 史乐峰, 张谦, 等(Ren Yulong, Shi Lefeng, Zhang Qian, et al.). 电动汽车充电站最优分布和规模研究 (Optimal distribution scale of charging stations for electric vehicles) [J].电力系统自动化 (Automation of Electric Power Systems), 2011,35 (14): 53-57.

[14] 刘自发, 张伟, 王泽黎 (Liu Zifa, Zhang Wei, Wang Zeli). 基于量子粒子群优化算法的城市电动汽车充电站优化布局 (Optional planning of charging station for electric vehicle based on quantum PSO algorithm) [J]. 中国电机工程学报 (Proceedings of the CSEE), 2012, 32(22): 39-45, 20.

[15] 徐智威, 胡泽春, 宋永华, 等 (Xu Zhiwei, Hu Zechun, Song Yonghua, et al.). 基于动态分时电价的电动汽车充电站有序充电策略 (Coordinated charging strategy for PEV charging stations based on dynamic time-of-use tariffs) [J]. 中国电机工程学报 (Proceeding of the CSEE), 2014,34 (22): 3638-3646.

[16] 刘育红, 王曦 (Liu Yuhong, Wang Xi). “新丝绸之路”经济带交通基础设施与区域经济一体化——基于引力模型的实证研究(Confucian thinking of “Transforming Administration with Education” and contemporary Political Ethics transformation — with regard to political philosophy of “The Great Learning”)[J]. 西安交通大学学报 (社会科学版) (Journal of Xi’an Jiaotong University (Social Science)), 2014, 34(2): 43-48, 80.

[17] 倪冰洁 (Ni Bingjie). 基于引力模型的东海县农村用户点空间格局优化研究 (An optimizing research based on gravity model of the spatial pattern of rural residential areas in Donghai county) [D]. 南京: 南京师范大学(Nanjing: Nanjing Normal University), 2014.

[18] 徐刚 (Xu Gang). 面向我国经济技术开发区的投资引力模型及其应用研究 (Study on investment gravity model with it’s applications of China’s economic-technological development zone) [D]. 天津: 天津大学(Tianjin: Tianjin University), 2009.

Site planning of electric vehicles charging station based on gravity model

CHENG Hong-bo, XIAO Yong-le, WANG Xun, LUN Li, LI Ming-hui

(School of Electrical and Electronic Engineering, East China Jiaotong University, Nanchang 330013, China)

The construction of charging station should consider the investment revenue that is affected by the quantity of the EV and the charging times, while the quantity of the EV and the charging times are influenced by users’ convenience. Firstly, this paper proposed the EV quantity model based on gravity model after analyzing the relationship between EV quantity and the charging station’s grade, distance, and the EV scale. Secondly, the function of charging convenience is defined. Accordingly, the gravity relation between charging time and convenience is defined, then the site planning of charging station in the future based on the theory is considered. Finally, this model calculated by the differential evolution (DE) algorithm. Results of simulation and experiments demonstrated that the model of site planning of EV charging station is reasonable and conforms to the regional planning of urban and the distribution of the EV rallying point, and provide effective reference for site planning of EV charging station.

gravity model; EV charging station; site planning; charging times; convenience

2015-06-05

国家自然科学基金 (51267004)、 江西省自然科学基金(20132BAB216027)、 江西省教育厅(GJJ13356)、 华东交通大学校立课题(12DQ02)资助项目

程宏波(1979-)， 男， 湖北籍， 副教授， 博士， 研究方向为智能电网的互动及其控制; 肖永乐(1989-)， 男， 河北籍， 硕士研究生， 主要从事电动汽车充电站选址规划方面的研究。

TM715

A

1003-3076(2016)05-0061-06