品质因子可调小波变换在谐波/间谐波检测中的应用

张宇辉， 刘梦婕， 段伟润， 宋 娜

(1. 东北电力大学电气工程学院， 吉林省 吉林市 132012； 2. 国网天津市电力公司，天津 300010；3. 中国长江电力股份有限公司葛洲坝电厂， 湖北 宜昌 443002)

品质因子可调小波变换在谐波/间谐波检测中的应用

张宇辉1， 刘梦婕1， 段伟润2， 宋 娜3

(1. 东北电力大学电气工程学院， 吉林省 吉林市 132012； 2. 国网天津市电力公司，天津 300010；3. 中国长江电力股份有限公司葛洲坝电厂， 湖北 宜昌 443002)

为有效抑制多种噪声，将一种品质因子可调小波变换(TQWT)应用于谐波/间谐波检测中。首先利用谐波/间谐波信号与噪声信号品质因子的不同，从检测信号中分离出谐波/间谐波信号，然后根据奇异值差分谱进行模型定阶，采用总体最小二乘-旋转矢量不变技术(TLS-ESPRIT)实现谐波/间谐波信号参数的有效提取。分别针对数值仿真信号、实测电弧炉电流信号进行分析，结果表明：与总体经验模态分解相比，TQWT有效削弱了随机噪声和脉冲干扰，较好地保留了信号的主要特征；TQWT与TLS-ESPRIT算法相结合，提高了强噪声背景下谐波/间谐波参数的检测精度。

品质因子可调小波变换； 谐波； 间谐波； 消噪； 奇异值差分； TLS-ESPRIT

1 引言

电力电子装置和电弧炉等设备的使用产生了大量的谐波污染，影响电网的电能质量。准确检测谐波和间谐波，能够为谐波分析及其治理提供可靠依据。

文献[1,2]采用快速傅里叶变换对谐波、间谐波进行检测，通过插值、加窗在一定程度上消除了栅栏效应和频谱泄露，但需考虑窗函数旁瓣衰减特性。文献[3,4]利用人工神经网络非线性映射、自适应学习等特点将其应用于谐波分析，其中文献[4]采用激励函数参数可调的线性神经网络分析间谐波，精度较高，但需通过傅里叶分析确定神经网络中间谐波次数和个数的初始值。文献[5]提出了单子带重构算法，有效抑制了小波包变换在电力系统谐波检测中产生的频率混叠现象，但小波包变换的频域二分特性限制了其使用范围。文献[6]采用分段Prony算法确定各频段信号中谐波与间谐波参数，精度高于直接Prony算法，但对信噪比要求很高。文献[7]将总体经验模态分解(EEMD)应用到谐波检测中，削弱了经验模态分解(EMD)的模态混叠现象，但其本质是在EMD中添加高斯白噪声补充缺失尺度，因此当信号中2个组成分量的频率相近时，EMD无法将二者分开[8-10]，从而降低了EEMD的频率分辨率；同时，若信号中正、负脉冲干扰较强，会导致EEMD分解结果因脉冲干扰附近极值点不对称而出现模态混叠和虚假分量。

品质因子可调小波变换(TQWT)[11]根据瞬态冲击信号与持续周期振荡信号品质因子的不同，将复杂信号分解为包含周期振荡成分的高共振分量、包含瞬态冲击成分的低共振分量及包含其它成分的余项。本文将TQWT引入到噪声干扰背景下的谐波、间谐波检测中，研究TQWT在改善电力系统谐波、间谐波检测精度方面的可行性和有效性。

2 品质因子可调小波变换

信号的共振属性用品质因子Q进行定义，即

(1)

式中，f为信号中心频率；B为信号带宽。品质因子Q越小，信号的时间聚集性越好，共振属性越低；反之，Q越大，信号的频率聚集性越好，共振属性越高。区别于传统小波分析采用单一品质因子的基函数，TQWT对含有高、低共振属性的信号同时构建两种不同品质因子的小波基函数。瞬态冲击信号为宽带信号，品质因子低，而周期振荡信号为窄带信号，品质因子高，因此根据品质因子的差异，可实现周期振荡信号与瞬态冲击信号的分离。

信号的高共振分量通过具有高Q的基函数进行表示，同理，低共振分量通过具有低Q的基函数进行表示，并通过两通道滤波器组实现，如图1所示。

图1 品质因子可调小波变换两通道滤波器组Fig.1 Two channel filter banks for TQWT

图1中，高通尺度因子η=2/(Q+1)，低通尺度因子λ=1-η/r，其中r表示冗余度且0<η≤1，0<λ<1。子带信号k0(n)与k1(n)的采样频率分别为λfs和ηfs，其中fs为信号x(n)的采样频率。

以品质因子Q=5、分解层数L=12的品质因子可调小波变换为例，其频率响应如图2(a)所示。可以看出其频率响应为一组非恒定带宽的滤波器组。定义第j层尺度下的中心频率和带宽分别为：

(2)

(3)

图2 Q=5、L=12时品质因子可调小波变换频率响应与时域波形Fig.2 Frequency response and time-domain waveforms of TQWT with Q=5, L=12

由图2(a)及式(2)、式(3)可以看出，随着L增加，中心频率随之降低，相应带宽也随之减少。图2(b)为相应的小波时域图，从图中可以看出，随着L增加，小波的振荡时间随之变长。

考虑信号x由高共振属性信号x1及低共振属性信号x2构成，即

x=x1+x2x,x1,x2∈RN

(4)

信号x1和x2分别用基函数库Z1、Z2(Z1、Z2分别表示高、低品质因子可调小波变换的滤波器组)表示，利用形态分量分析[12]将对信号x的分解转换为约束最优化问题，即

J(θ1,θ2)=‖x-Z1θ1-Z2θ2‖+

μ1‖θ1‖1+μ2‖θ2‖1

(5)

(6)

噪声干扰抑制可转化为实现谐波、间谐波信号与噪声信号的分离。脉冲干扰时间聚集性好，品质因子较小，而谐波和间谐波信号频率聚集性好，品质因子较大，因此，通过二者品质因子的差异可以将含噪信号分解为包含谐波、间谐波成分的高共振分量和包含脉冲干扰的低共振分量以及包含其它干扰的余项。

3 TLS-ESPRIT原理与奇异值差分谱

总体最小二乘-旋转矢量不变(TLS-ESPRIT)算法[13]假设采样信号由p个正弦信号和白噪声组成，即

(7)

式中，ck=akejθk，zk=e(-σk+j2πfk)Ts，其中Ts为采样周期，ak、θk、σk和fk分别为第k个振荡模态的幅值、相位、衰减系数和频率；s2(n)为白噪声。由于采样信号为实信号，p通常为实际正弦分量个数的2倍。

由采样数据s(n)构造HANKEL矩阵：

(8)

式中，l+m-1=N，N为采样点数。对矩阵H进行奇异值分解：

H=UAVT

(9)

式中，U和V均为正交阵；A为对角阵，其对角元素为A的奇异值，并按降序排列。V按奇异值大小划分为信号子空间Vs和噪声子空间Vn。Vs删除第一行和最后一行形成的矩阵分别为V1和V2，考虑噪声干扰有

V1+e1=(V2+e2)Φ

(10)

式中，e1和e2为误差矩阵；Φ为旋转算子。

根据Φ可获得信号参数，通过TLS对Φ寻优使得误差矩阵e1和e2的总体误差‖e1,e2‖最小。对(V1,V2)构成的矩阵进行奇异值分解：

(11)

将M分成4个p×p矩阵：

(12)

求取M11M21-1的特征值εk(k=1,2,…,p)可估计信号中各分量的频率：

(13)

进一步通过最小二乘法求取幅值等信息，对于N点采样信号：

s=βc

(14)

由最小二乘法得：

c=(βTβ)-1βTs

(15)

式中，β和c的解释详见文献[13]。信号中各分量的幅值和相位分别为：

(16)

θk=angle(c)

(17)

TLS-ESPRIT算法的关键在于信号子空间和噪声子空间的划分，即求HANKEL矩阵的有效秩p。实际应用中，噪声导致的奇异值并不都等于0，因此，p取决于非零奇异值的合适选取。若p值过大，则会出现虚假模态，反之会出现模态遗漏。文献[14]提出一种奇异值差分谱，根据差分谱峰值位置实现对信号中有用分量个数的确定，本文将其用于TLS-ESPRIT算法的模型定阶。

将矩阵A对角元素的奇异值从大到小排列，相邻奇异值两两相减，即

Di=σi-σi+1

(18)

式中，σi为奇异值序列第i个奇异值。所有Di形成的序列即为奇异值差分谱，当Di的值平稳趋于0时，对应的奇异值阶数即为模型的真实阶次。

4 检测方法步骤

(1)对含有噪声干扰的谐波和间谐波信号，选取高共振品质因子Q1、低共振品质因子Q2进行品质因子可调小波变换(Q1一般取5，Q2取1即可)，实现谐波、间谐波信号和噪声信号的分离。

(2)利用奇异值差分谱估计TLS-ESPRIT阶次。

(3)对步骤(1)中得到的高共振分量计算各谐波、间谐波的频率和幅值等参数。

5 仿真分析

5.1 谐波和间谐波信号的数值仿真

设含噪信号为：

(19)

式中，n(t)由4个幅值分别为-5A、-3A、+3A、+5A的脉冲干扰以及5%的随机噪声组成，采样频率为2kHz，加入噪声后的信号波形如图3所示。

采用品质因子可调小波变换对图3中的信号进行分解，得到的高、低共振分量及余项如图4所示。

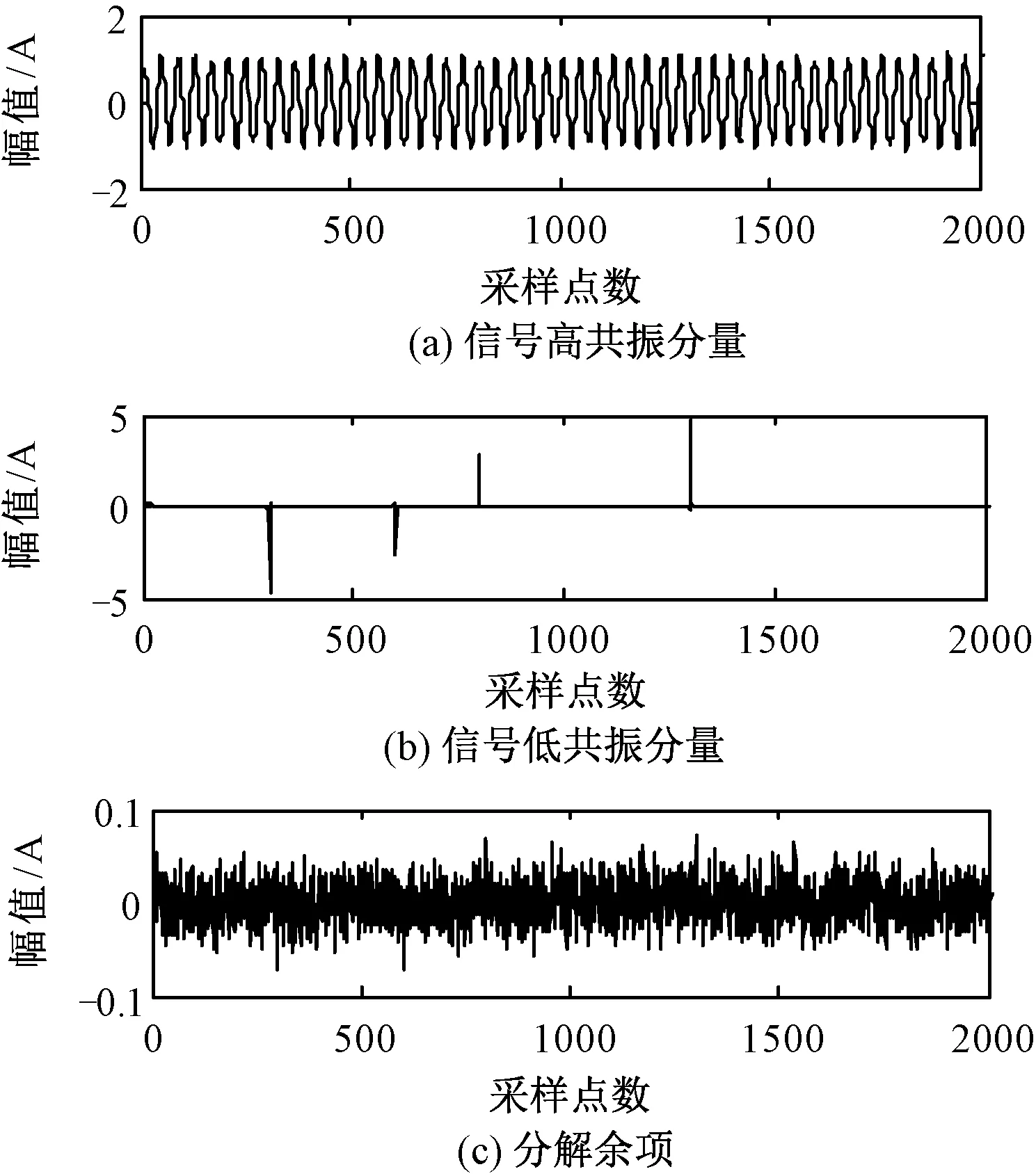
图4 仿真信号分解结果Fig.4 Separation result of simulation signal

比较图3和图4可以看出，高共振分量以谐波和间谐波为主，低共振分量则以脉冲干扰为主，分解余项主要为随机噪声成分。图5为高共振分量与不含噪声干扰的理想信号局部对比图。

图5 高共振分量与理想信号局部对比图Fig.5 Local contrast figure of high resonance component and ideal signal

由图4和图5可以看出，TQWT在有效抑制噪声干扰的同时，较好地保留了信号的主要特征。采用奇异值差分谱确定图4(a)信号的阶数为10，TLS-ESPRIT对谐波和间谐波参数检测的结果如表1所示。

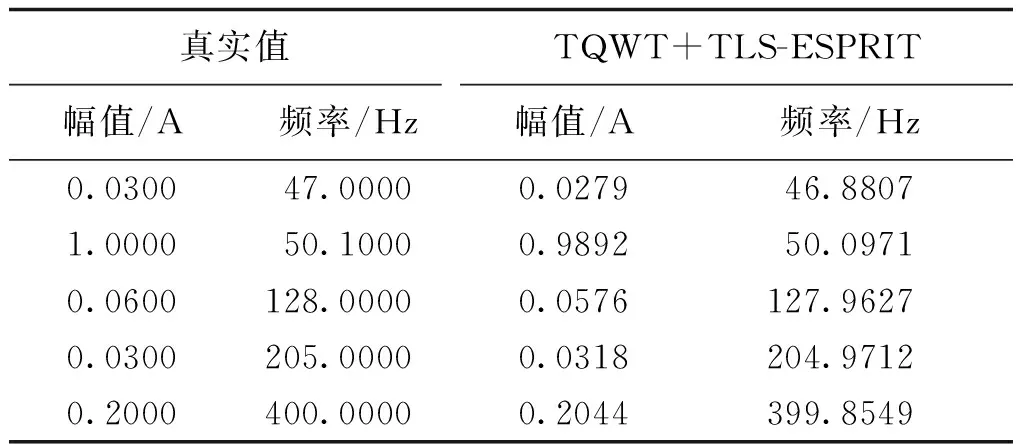
表1 频率及幅值计算结果1Tab.1 Calculation results 1 of frequency and amplitude

由表1可以看出，本文方法检测精度较高，且TLS-ESPRIT利用奇异值差分谱定阶后，较好地识别出了频率相近的47Hz和50.1Hz分量参数。

作为对比，采用EEMD对图3所示信号进行分解，得到的各阶固有模态分量如图6所示。

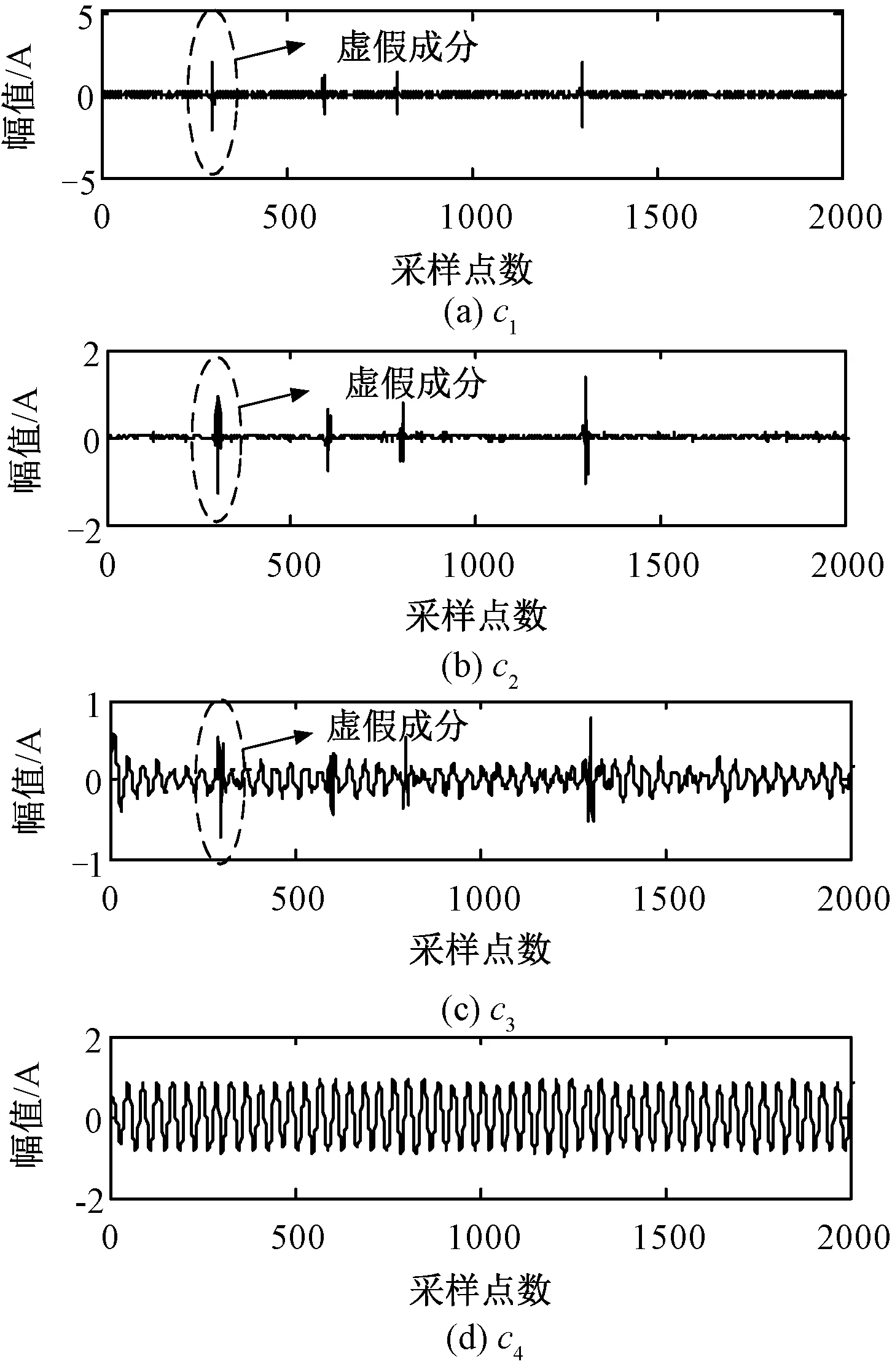
图6 EEMD分解结果Fig.6 Decomposition result of EEMD

由图6可以看出，固有模态分量c1、c2和c3中的脉冲干扰极性发生明显变化，出现了虚假成分。同时，对各固有模态分量进行频谱分析发现，c1中存在400Hz谐波，c2中存在频率尺度差异较大的205Hz间谐波和400Hz谐波，c3中存在频率尺度差异较大的50.1Hz基波和128Hz间谐波，而c4中47Hz间谐波受50.1Hz基波频谱泄露影响无法检测。

上述分析表明：①强脉冲干扰导致信号局部极值点不对称，增大了上、下包络线的拟合误差，从而出现了虚假分量和模态混叠；②EEMD无法分离频率尺度相近的47Hz间谐波与50.1Hz基波，进而无法提取出基波分量。

5.2 实例分析

采用文献[15]的实际电弧炉电流信号，信号中含有25Hz、50Hz和125Hz频率分量，幅值分别为64.933A、100A和74.813A。向其中添加方差为12的随机噪声和幅值分别为-100A、+100A的脉冲干扰，波形如图7所示。以+100A脉冲干扰出现时刻为例，采用品质因子可调小波变换消噪前后的局部波形如图8所示。

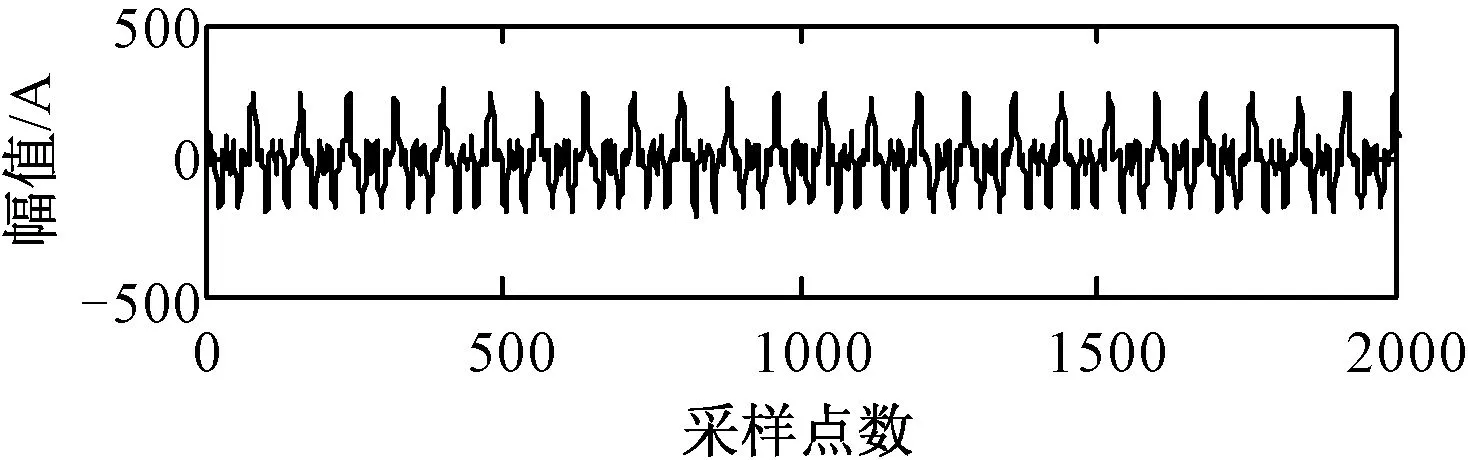
图7 电弧炉信号Fig.7 Electric current signal of arc furnace

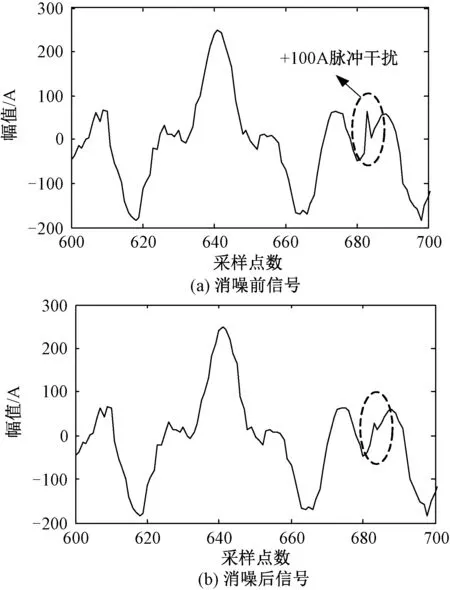
图8 电弧炉信号消噪前后局部对比图Fig.8 Partial contrast figure of electric current signal of arc furnace before and after de-noising

由图8可以看出，品质因子可调小波变换对信号中的脉冲干扰和随机噪声具有明显抑制效果。表2为采用本文方法与直接采用TLS-ESPRIT算法分析电弧炉信号的结果对比，可以看出，本文方法在多种噪声干扰下较好地检测出了各频率分量参数，精度上高于直接TLS-ESPRIT算法。

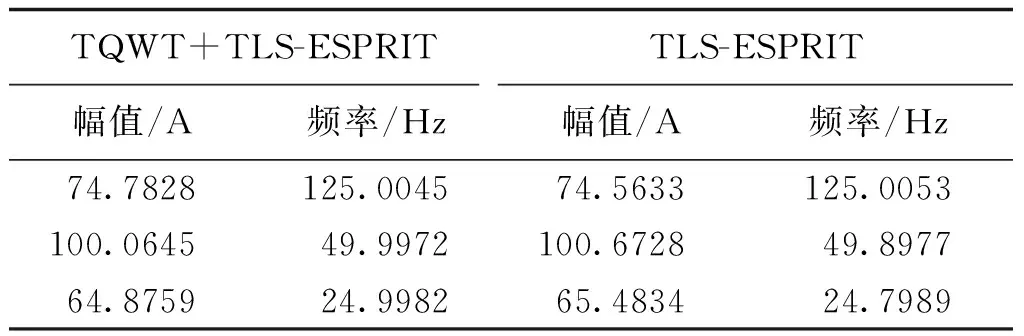
表2 频率及幅值计算结果2Tab.2 Calculation results 2 of frequency and amplitude

6 结论

本文将一种品质因子可调小波变换应用于谐波、间谐波信号检测中，研究结果表明：

(1)利用谐波、间谐波信号与噪声信号品质因子的不同，实现了噪声信号与谐波、间谐波信号的有效分离，结合TLS-ESPRIT算法提高了强噪声背景下的谐波、间谐波检测精度，具有良好的应用前景。

(2)与EEMD相比，不存在模态混叠和虚假分量，有效抑制多种噪声的同时，较好地保留了信号的主要特征。

(3)TLS-ESPRIT结合奇异值差分谱，可以准确确定模型阶次，相比EEMD实现了频率尺度相近的谐波、间谐波参数检测。

[1] 盛占石，谭斐，潘天红 (Sheng Zhanshi, Tan Fei, Pan Tianhong). 谐波分析的改进双峰谱线算法 (Improved double peak of spectral lines algorithm for analysis of power system harmonics) [J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2008，27(2)：47-50，58.

[2] 翟瑞淼， 英超， 任国臣， 等(Zhai Ruimiao, Ying Chao, Ren Guochen, et al.). 基于Nuttall窗的三峰插值谐波算法分析 (An approach for harmonic analysis based on Nuttall window and triple-spectral-line interpolation) [J]. 电力系统保护与控制 (Power System Protection and Control)，2015，43(10)：38-43.

[3] 李德超 (Li Dechao). 一种基于BP神经网络的快速谐波分析算法研究(Study of fast harmonic analysis algorithm based on BP neural network) [J]. 电瓷避雷器(Insulators and Surge Arresters)，2014， (6)：67-71.

[4] 王好娜， 毕志周， 付志红， 等 (Wang Haona, Bi Zhizhou, Fu Zhihong, et al.). 基于BP神经网络和线性神经网络的间谐波分析方法 (Analysis approach for inter-harmonic with BP neural network and linear neural network) [J]. 高压电器 (High Voltage Apparatus)，2013， 49(2)：19-24.

[5] 尚秋峰， 康丹， 李青， 等 (Shang Qiufeng, Kang Dan, Li Qing, et al.). 基于单节点重构改进小波包的电力系统谐波分析算法(Power system harmonic analysis algorithm based on wavelet packet improved by single-node reconstruction) [J]. 电力系统保护与控制(Power System Protection and Control)，2011，39(3)： 74-77，94.

[6] 郭成,李群湛,贺建闽,等 (Guo Cheng, Li Qunzhan, He Jianmin, et al.). 电网谐波与间谐波检测的分段Prony算法 (Segmentation Prony algorithm on harmonics and inter-harmonics detection of power networks) [J]. 电网技术 (Power System Technology)，2010，34(3)：21-25.

[7] 朱宁辉, 白晓民, 董伟杰 (Zhu Ninghui, Bai Xiaomin, Dong Weijie). 基于EEMD的谐波检测方法(Harmonic detection method based on EEMD) [J]. 中国电机工程学报 (Proceedings of the CSEE)，2013, 33(7): 92-98.

[8] 李成鑫, 刘俊勇, 姚良忠, 等 (Li Chengxin, Liu Junyong, Yao Liangzhong, et al.). 基于改进频移经验模态分解的低频振荡参数提取(Extraction of low frequency oscillation parameters based on refined frequency shift empirical mode decomposition) [J]. 电力系统自动化 (Automation of Electric Power Systems)，2012, 36(15): 8-13.

[9] N Senroy，S Suryanarayanan，P F Ribeiro. An improved Hilbert-Huang method for analysis of time-varying waveforms in power quality [J]. IEEE Transactions on Power Systems, 2007, 22(4): 1843-1850.

[10] D S Laila, A R Messina, B C Pal. A refined Hilbert-Huang transform with applications to inter-area oscillation monitoring [J]. IEEE Transactions on Power Systems, 2009, 24(2): 610-620.

[11] I W Selesnick. Wavelet transform with tunable q-factor [J]. IEEE Transactions on Signal Processing, 2011, 59(8): 3560-3575.

[12] J Bobin, J L Starck, J M Fadili, et al. Morphological component analysis: An adaptive thresholding strategy [J]. IEEE Transactions on Image Processing, 2007, 16(11): 2675-2681.

[13] 王曦,李兴源,王渝红,等 (Wang Xi, Li Xingyuan, Wang Yuhong, et al.). 基于TLS-ESPRIT辨识的多直流控制敏感点研究 (Analysis on controllability sensitive points of multi-HVDC systems based on TLS-ESPRIT method) [J]. 电力系统保护与控制 (Power System Protection and Control), 2012, 40(19): 121-125.

[14] 赵学智, 叶邦彦, 陈统坚 (Zhao Xuezhi, Ye Bangyan, Chen Tongjian). 奇异值差分谱理论及其在车床主轴箱故障诊断中的应用 (Difference spectrum theory of singular value and its application to the fault diagnosis of headstock of lathe) [J]. 机械工程学报 (Journal of Mechanical Engineering), 2010,46(1): 100-108.

[15] Zbigniwe L, Tadeusz L, Jacek R. Advanced spectrum estimation methods for signal analysis in power electronics [J]. IEEE Transactions on Industrial Electronics, 2003, 50(3): 514-519.

Application of tunableQ-factor wavelet transform in detecting harmonic and inter-harmonic

ZHANG Yu-hui1, LIU Meng-jie1, DUAN Wei-run2, SONG Na3

(1. School of Electrical Engineering, Northeast Dianli University, Jilin 132012, China;2. State Grid Tianjin Electric Power Company, Tianjin 300010, China;3. Gezhouba Hydropower Plant, China Yangtze Power Co., Ltd., Yichang 443002, China)

To effectively suppress various noises, a tunableQ-factor wavelet transform (TQWT) is applied to harmonic and inter-harmonic detection. Using the distinctQ-factor of harmonic and inter-harmonic signal and noise signal to isolate harmonic and inter-harmonic from detection signal, and setting model order based on singular value difference spectrum, the effective extraction of the harmonic and inter-harmonic signal parameters is realized by using total least squares-estimation of signal parameters via rotational invariance techniques (TLS-ESPRIT). Analyzing numerical simulation signals and measured current signal of electric arc furnace respectively, the results show that compared with the ensemble empirical mode decomposition, TQWT can effectively weaken the random interference and pulse interference, and better retain the main features of the signal; and combined with the TLS-ESPRIT algorithm TQWT will improve the parameter detection accuracy of harmonic and inter-harmonic under the background of strong noise.

tunableQ-factor wavelet transform；harmonic；inter-harmonic；de-noising；singular value difference；TLS-ESPRIT

2015-06-08

东北电力大学研究生创新基金(Y2014002)资助项目

张宇辉(1962-)， 男， 吉林籍， 副教授， 硕士， 研究方向为自动控制理论、 信号处理在电力系统中的应用； 刘梦婕(1988-)， 女， 吉林籍， 硕士研究生， 研究方向为非线性系统理论在电力系统中的应用。

TM714

A

1003-3076(2016)05-0055-06