考虑变压器接线方式的电能质量监测装置优化配置方法

刘 平， 欧阳森， 蔡东阳

(华南理工大学电力学院， 广东 广州 510640)

考虑变压器接线方式的电能质量监测装置优化配置方法

刘 平， 欧阳森， 蔡东阳

(华南理工大学电力学院， 广东 广州 510640)

当前电能质量监测装置配置过程尚未考虑变压器接线方式对电压暂降传播特性影响，针对这一缺陷，本文首次提出一种考虑变压器接线方式的电能质量监测装置的优化配置方法。首先深入分析系统中变压器不同接线方式对电压暂降传播特性的影响，建立与特定接线方式相对应的电压暂降幅值矩阵。然后，构建了各种类型短路故障下的电压暂降可观测矩阵，形成保证全网各节点电压暂降可观的约束条件，以监测装置数量最小为目标函数，建立了基于遗传算法的电能质量监测装置优化配置方法。最后，对IEEE-39节点进行仿真计算，验证了本文方法的有效性。

变压器接线方式； 电能质量监测装置； 可观测矩阵； 配置方案； 遗传算法

1 引言

与谐波、三相不平衡等稳态电能质量问题相比，近年来电压暂降事件发生频度更多、危害更大，已成为影响设备正常稳定运行的最严重的电能质量问题。另一方面，各种敏感设备目前在电力系统中大量广泛应用，系统中很多节点开始作为电压暂降敏感节点而存在[1-3]。考虑到电力系统规模庞大，在每个节点均配置电能质量监测装置耗费巨大成本，同时产生大量监测数据增加了信息传输与处理的难度[4-6]。因此，优化配置电能质量监测装置，通过在系统中若干节点配置监测装置，实现对系统所有节点电压暂降的监测，具有重要的现实意义。

国内外学者对此开展了大量研究，并有不少卓有成效的成果，包括规划法[7]、相关法[8]、演化算法[9]、故障识别法[10]和整数线性规划法[11-15]等，但这些方法都还存在一些缺陷，例如文献[7,8]所提方法适用于稳态电能质量，而无法对电压暂降问题进行监测；文献[9]提出方法得到的优化结果并不能保证对所有故障引起的电压暂降事件的监测。目前所研究的各类方法得到的最终优化配置方案严重依赖于电压暂降可观测矩阵[11-15](又称凹陷域矩阵)，但这些方法在计算电压暂降可观测矩阵的过程中都没有研究变压器接线方式对电压暂降传播特性的影响，甚至都没有明确提及与最终优化配置方案相对应的变压器接线方式，而实际系统中变压器接线方式的不同会导致电压暂降可观测域差异明显[16-19]，因此必然会影响这些方法的优化配置结果的准确性。

基于此，本文首次提出了考虑变压器接线方式的电能质量监测装置的优化配置方法。首先通过深入分析变压器接线方式对电压暂降传播特性的影响，说明电压暂降幅值矩阵与变压器接线方式密切相关；然后构建基于某种特定接线方式的电压暂降幅值矩阵，并计算出相应的各种故障情况下的可观测矩阵，形成全网各节点电压暂降可观的约束条件，以监测装置数量最小为目标函数，建立基于遗传算法的电能质量监测装置优化配置方法。最后，对IEEE-39节点进行了仿真计算，验证了本文方法的有效性。

2 变压器接线方式对电压暂降传播特性的影响

2.1 定义传播矩阵

对于系统中某一变压器而言，定义其一次侧及二次侧相电压之间的传播关系为：

Vabc=TVABC

(1)

式中，VABC=[VAVBVC]T为变压器一次侧三相电压的标幺值；Vabc=[VaVbVc]T为变压器二次侧三相电压的标幺值；T为相电压通过变压器的传播矩阵。

用VABC(+-0)、Vabc(+-0)表示变压器一、二次相电压的正、负、零序分量，由对称分量法可知，相电压与其序分量之间的关系为：

VABC=SVABC(+-0)

(2)

Vabc=SVabc(+-0)

(3)

式中，变换矩阵S为：

(4)

其中，运算子a=ej120°，a2=ej240°。

变压器一次侧与二次侧相电压序分量之间的关系为：

Vabc(+-0)=HVABC(+-0)

(5)

式中，H为变压器三序电压传播矩阵。

由式(1)～式(5)可推算变压器两侧相电压的关系为：

Vabc=SHS-1VABC

(6)

即T与H的关系为：

T=SHS-1

(7)

2.2 变压器接线方式分类

电压暂降在渗透传播经过变压器后，其特性(主要是幅值、相角)可能会发生突变，且变化情况与变压器接线方式密切相关[16]。电力系统中由不对称短路故障引发电压暂降时，电压暂降特性中包含零序分量，而Y0/Y-12、Y/Y-12、Y/Δ-11和Y0/Δ-11等接线方式的变压器不允许零序分量电流通过，无法传递零序电压，从而导致电压暂降特性发生突变。因此，本文根据变压器能否传递零序分量，将变压器按接线方式分为两种类型，即I型和II型，并推导每种类型变压器的相电压传播矩阵T。

(1)I型变压器

变压器接线方式为两侧中性点接地，常见联结方式为Y0/Y0-12，允许零序分量通过，即三序电压传播矩阵为单位矩阵E，代入式(7)可得相应的相电压传播矩阵T1为：

T1=E

(8)

(2)II型变压器

变压器接线方式为至少一侧中性点不接地，此时不允许零序分量通过，相应的三序电压传播矩阵为非单位阵。文献[17]根据具体的联结方式又将II型变压器分为两种类型，即IIA和IIB型，前者常见的联结方式为Y0/Y-12、Y/Y0-12、Y/Y-12，后者为Y/Δ-11、Y0/Δ-11。对应的三序电压传播矩阵H2和H3分别为：

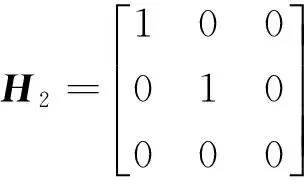
(9)

代入式(7)，可得相应的T2和T3为：

(10)

可见，变压器接线方式对电压暂降传播特性有着重要影响，同一电压暂降信号传播经过不同接线方式的变压器后，其特性会有不同程度变化。对于I型变压器，其相电压传播矩阵T1为单位阵，说明电压暂降通过该类型变压器后特性保持不变；对于II型变压器，其相电压传播矩阵T2、T3为非单位阵，说明电压暂降通过该类型变压器后特性会发生突变。因此，在计算电压暂降幅值矩阵过程中，必须要重点考虑系统中变压器接线方式。

3 电压暂降幅值矩阵计算

在参考借鉴现有文献[12,20]基础上，本文给出电压暂降幅值矩阵计算步骤：

(1)明确系统中各台变压器接线方式；

(2)结合故障点、故障类型和变压器接线方式，做出其三序(正、负、零序)等值电路，并结合其他元件三序模型，构建三序网络模型，分别形成三序节点导纳矩阵Y+、Y-、Y0；

(3)对节点导纳矩阵求逆，可得到对应的节点阻抗矩阵Z+、Z-、Z0；

(4)根据节点阻抗矩阵中元素，利用文献[20]推导的各种短路故障下电压幅值解析式，可得与系统变压器接线方式及故障类型相对应的单相短路接地故障、两相短路故障、两相短路接地故障、三相短路故障电压暂降幅值矩阵V1p、V2p、V2pg、V3p。

需要说明的是，变压器接线方式的改变会导致系统零序网络发生变化。对两相短路故障而言，运用对称分量法求取三序网的复合序网中只包含正序网络和负序网络，而三相短路故障只存在正序网络，因此变压器接线方式改变对这两种故障类型并没有多大影响，即当变压器接线方式变化时，仅需要对上述计算步骤中的V1p、V2pg进行修正即可。

4 监测装置优化配置

4.1 定义状态向量

对于n节点的系统，每个节点是否安装电能质量监测装置，可用一个n维行向量X来表示：

X=[x1x2…xn-1xn]

(11)

X为二进制向量，它的元素只能是1或0，当节点i处安装电能质量监测装置时xi为1(i=1，2，…,n)，反之为0。

4.2 构建可观测矩阵

可观测域是指系统发生短路故障引起某一监测点m出现电压暂降时，该监测点所能观测到的故障点区域。换句话说，监测点m的可观测域内任一节点的短路故障都会引起m发生电压暂降[11-15]。若故障点遍及全网，可观测域可用一个n×f阶0-1矩阵M进行描述，称为可观测矩阵：

(12)

式中，Vt为电压暂降阈值电压；Vij为故障点j发生故障时节点i的电压；n为网络节点数目；f为故障点数目。发生不同类型故障时，可根据V1p、V2p、V2pg、V3p中元素，构建与系统中变压器接线方式相对应的不同故障类型下的可观测矩阵M1p、M2p、M2pg、M3p。

4.3 建立优化模型

电能质量监测装置优化配置的目标是监测装置数量最小，故目标函数的数学表达式为：

(13)

若系统中存在重要负荷点或者枢纽点，必须安装电能质量监测装置，预先设定向量X中对应元素为1。

为保证系统电压暂降的可观性，当系统发生任意一种类型故障时，要求至少有一台监测装置可以捕获此次暂降事件。换句话说，向量X乘以可观测矩阵M1p、M2p、M2pg、M3p的每一列得到的值必须大于或者至少等于1，可得与系统中变压器接线方式相对应的束条件：

(14)

采用目前常用于求解整数线性规划问题的遗传算法，对式(13)和式(14)所构成的优化模型进行求解。需要注意的是，该模型可能存在多组解，需要进一步优化确定最终配置方案。而实际情况中，一般电压等级高、容量大的节点处的地位更重要，常优先作为监测对象，将每个节点的电压等级和额定容量的倒数求和作为权重值[14]，即：

(15)

式中，c为权重值；h为多组优化解的配置节点；Vi为节点i电压；Si为节点i容量。比较多组配置方案的权重值，其中c最小的配置方案即确定为最终配置方案。

5 算例仿真与分析

本文以IEEE39节点系统(如图1所示)为例，根据优化模型，通过MATLAB编程进行仿真计算，分析变压器接线方式对电压暂降可观测域及电能质量监测装置配置方案的影响。

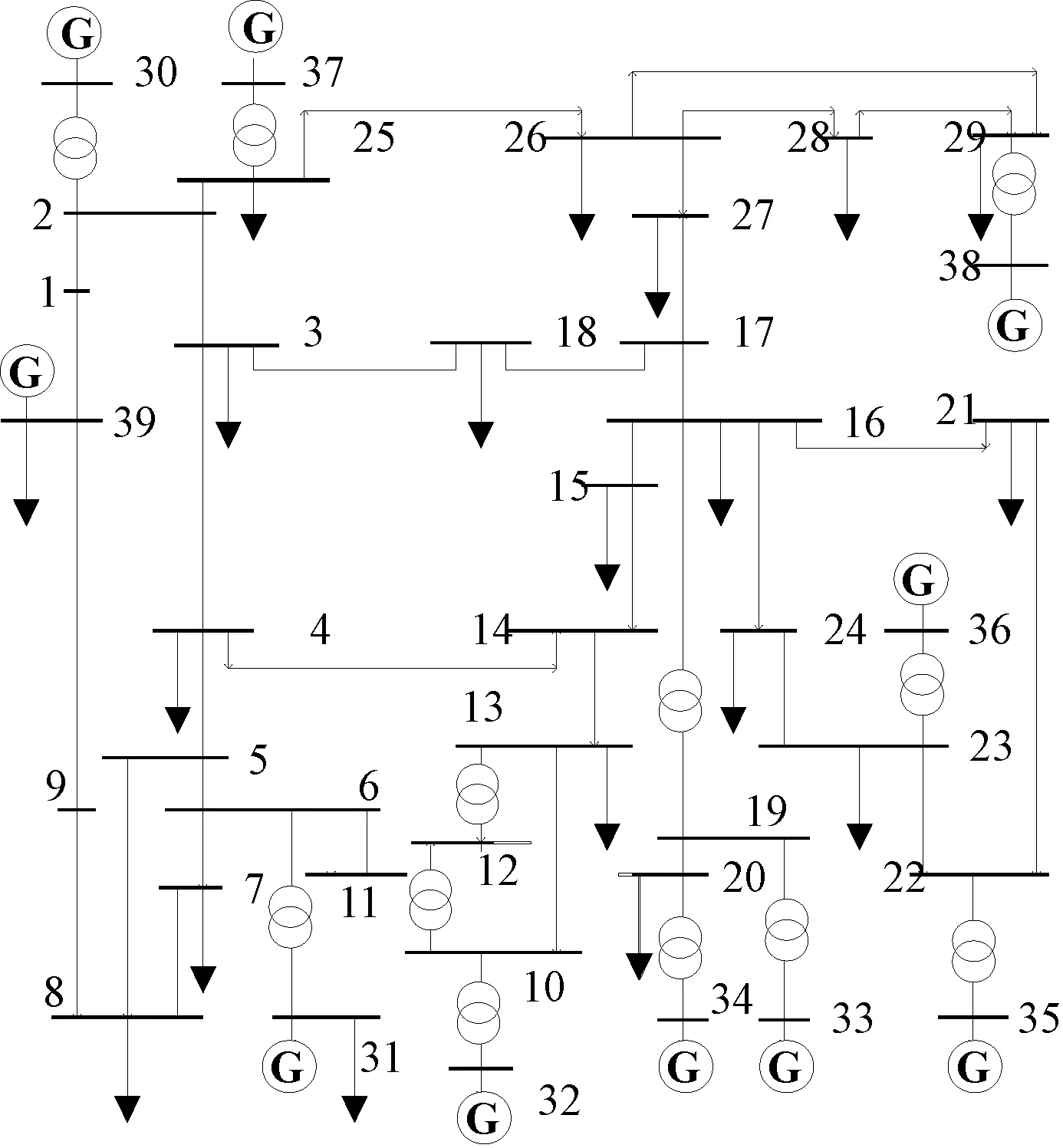
图1 IEEE39节点系统Fig.1 IEEE 39-bus system

5.1 变压器接线方式对电压暂降可观测域的影响

随机选取IEEE39节点系统中的节点9作为监测点，监测1～29号节点的电压暂降情况，取电压暂降阈值电压Vt=0.9pu，通过改变变压器的接线方式进行多次仿真。由于系统中12个变压器接线方式有多种组合，鉴于篇幅所限，本文选择以下5类典型接线方式进行仿真分析：

(1)系统中所有变压器接线方式均为I型，即中性点接地，联结方式均为Y0/Y0-12；

(2)系统中所有变压器接线方式均为IIA型，即中性点不接地，且联结方式均为Y/Y-12；

(3)系统中所有变压器接线方式均为IIB型，即中性不接地，且联结方式均为Y/Δ-11；

(4)系统中有6台变压器接线方式为I型，其余的为IIA型；

(5)系统中有6台变压器接线方式为I型，其余的为IIB型。

以单相短路接地故障为例进行分析。表1给出了在不同变压器接线方式下，节点9的电压暂降可观测域的仿真结果，即节点1～29发生单相短路接地故障时，节点9的电压暂降可观测域内包含的节点。

表1 不同接线方式下发生单相短路接地故障时节点9的电压暂降可观测域内包含的节点
Tab.1 Nodes in bus-9 observable area under different connection modes of transformers with single-phase grounding fault

接线方式节点9的电压暂降可观测域内包含的节点均为I型1,2,3,4,5,6,7,8,9,10,11,12,13,14,30,31,32,39均为IIA型1,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,31,32,39均为IIB型1,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,31,39I、IIA混合型1,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,31,32,39I、IIB混合型1,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,31,39

分析表1中数据可知：①变压器接线方式均为I、IIA、IIB型时，节点9处可观测到的节点数目分别是18、21、19；②不论变压器为何种接线方式，节点9始终能观测到的节点分别是1、4、5、6、7、9、10、12、13、14、31、39等12个；③发生单相短路接地时，电压暂降可观测域随着系统中变压器接线方式变化而变化，这是由于此时运用对称分量法求复合序网络模型时含有零序网络，而变压器接线方式不同，零序网络模型也不同[21]，因此电压暂降可观测域不同。

此外，由表1还可看出，发生单相短路故障时，与变压器接线方式均为I型(即中性点接地)相比，变压器接线方式均为IIA型或IIB型(即中性点不接地)时节点9的电压暂降可观测域包含的节点个数更多。说明与中性点接地的接线方式相比，中性点不接地时对应的电压暂降可观测域较大。

然而，现有文献在计算电压暂降可观测域过程中，并没有明确变压器接线方式，而实际上同一系统中变压器接线方式的不同会导致可观测域差异明显，并影响到最终配置方案。

5.2 优化配置方法

利用本文所述优化配置方法，选取电压暂降阈值电压Vt为0.9pu，在不同接线方式下采用MATLAB编程仿真计算，可得到监测装置的最终配置方案(即监测装置数量和安装位置)。文献[12]利用传统配置方法，未考虑变压器接线方式对监测装置配置的影响，同样选取Vt为0.9pu对IEEE39节点系统进行研究分析。基于以上两种方法的监测装置配置方案对比如表2所示。

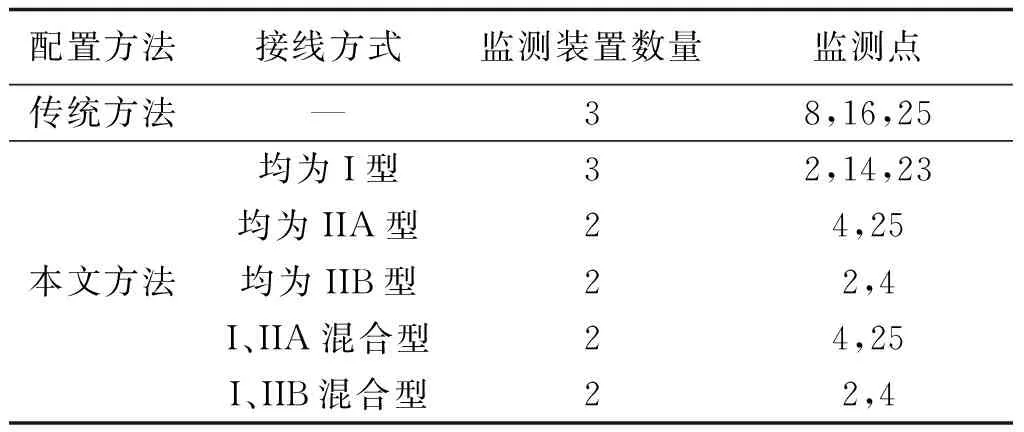
表2 不同配置方法下监测装置配置方案对比Tab.2 Comparison between optimal number and location of monitoring buses under different methods

由表2可知，利用传统方法进行优化配置时，由于未考虑变压器接线方式的影响，因此仅能得到固定的监测装置配置方案，无法进行进一步的优化，结果未必可靠。采用本文方法进行优化配置时，深入研究了变压器接线方式，充分考虑运用对称分量法分析短路故障时零序网络的影响，发现变压器接线方式确实会对最终配制方案造成影响。进一步分析配置结果，可得到以下结论：①变压器接线方式不同，监测装置的最终配置方案不同，说明了配置方案与系统中变压器的接线方式密切相关；②中性点不接地(即变压器接线方式均为IIA型或IIB型)时，监测装置数量为2，中性点接地(即变压器接线方式均为I型)时，监测装置数量为3，这是由于与中性点不接地的接线方式相比，中性点接地时对应的电压暂降可观测域较小，因此所需监测装置数量较多。

此外，还可以看到，对于变压器均为I型接线方式的系统而言，改变部分变压器接线方式，即接线方式变为I、IIA混合型或者I、IIB混合型，可进一步减少监测装置数量。说明在满足变压器安全性、稳定性等方面的前提下，适当改变系统中部分变压器接线方式，使更多的变压器处于中性点不接地的接线方式，可实现对监测装置配置方案的进一步优化，有效降低投资成本。

6 结论

(1)系统中变压器接线方式对电压暂降可观测域有重要影响。发生单相短路接地故障或两相短路接地故障时，与中性点接地(I型)接线方式相比，中性点不接地(IIA型、IIB型)时对应的电压暂降可观测域较大。

(2)电能质量监测装置的配置方案与系统中变压器接线方式密切相关。与中性点不接地的接线方式相比，中性点接地时所需的监测装置数量较多。

(3)在满足系统安全性、稳定性等方面前的提下，适当改变系统中部分变压器接线方式，使更多的变压器处于中性点不接地的接线方式，可实现对监测装置配置方案的进一步优化。

本文着重讨论了变压器的接线方式对电能质量监测装置的配置的重要影响，此外电网接线方式、故障电阻大小等因素也会对监测装置的配置产生影响，这也是未来需要进一步深入研究的课题。

[1] 杨家豪，欧阳森，石怡理，等(Yang Jiahao，Ouyang Sen，Shi Yili，et al.)．一种组合隶属度函数及其在模糊评价中的应用(Combined membership function and its application on fuzzy evaluation of power quality)[J]．电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2014，33(2)：63-68.

[2] 谢康，杨洪耕，黄静，等(Xie Kang，Yang Honggeng，Huang Jing，et al.)．基于本体的电能质量监测信息智能检索模型(Ontology-based intelligent retrieval model for power quality monitoring information)[J]．电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2013，32(1)：108-112.

[3] Milanovic J V，Gupta C P．Probabilistic assessment of financial losses due to interruptions and voltage sags - Part I : The methodology [J]．IEEE Transactions on Power Delivery，2006，21(2)：918-924.

[4] 滕志军，王中宝，索大翔，等(Teng Zhijun，Wang Zhongbao，Suo Daxiang，et al.)．变电站电能质量在线监测系统(On-line monitoring system for substation power quality)[J]．电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2013，32(2)：97-102.

[5] 陈武，刘慧敏，陈宾(Chen Wu，Liu Huimin，Chen Bin)．智能电网背景下电压暂降监测装置的最优布点方法(Optimal distribution method of voltage sag monitoring device in smart grid)[J]．电力建设(Electric Power Construction)，2011，32(6)：18-22.

[6] 王玲，康健，邹宏亮，等(Wang Ling，Kang Jian，Zou Hongliang, et al.)．实时电能质量监测系统的构建与应用(Construction and application of real-time power quality monitoring system)[J]．电力系统保护与控制(Power System Protection and Control)，2011，39(2)：108-110.

[7] Eldery M A．A novel power quality monitoring allocation algorithm[J]．IEEE Transactions on Power Delivery，2004，21(2)：768-777.

[8] Eldery M A，El-Saadany F，Salama M M A．Optimum number and location of power quality monitors[A]．11th International Conference on Harmonics and Quality of Power [C]. Lake Placid, NY，USA，2004.

[9] Nelson Kagan N M，Matsua E L，Ferrari J C．Allocation of power quality meters for voltage sag estimation using evolutionary algorithms[A]．19th International Conference on Electricity Distribution [C]. 2007. 21-24.

[10] 谭丹，杨洪耕(Tan Dan，Yang Honggeng)．基于故障识别法的电压暂降监测点的优化配置(An optimum allocation of voltage sag monitor based on fault recognition method)[J]．电力系统保护与控制(Power System Protection and Control)，2013，41(20):7-10.

[11] 吕伟，田立军(Lv Wei，Tian Lijun)．基于凹陷域分析的电压暂降监测点优化配置(Optimal allocation of voltage sag monitoring based on exposed area analysis)[J]．电力自动化设备(Electric Power Automation Equipment)，2012，32(6)：45-50.

[12] 周超，田立军(Zhou Chao，Tian Lijun)．基于粒子群优化算法的电压暂降监测点优化配置(An optimum allocation method of voltage sag monitoring nodes based on particle swarm optimization algorithm)[J]．电工技术学报(Transaction of China Electrotechnical Society)，2014，29(4)：181-186.

[13] 代晓倩，杨洪耕，蔡维(Dai Xiaoqian，Yang Honggeng，Cai Wei)．一种考虑电压暂降分布域的电能质量监测仪的优化配置方法(One optimum allocation of power quality monitors by considering exposed area)[J]．电力科学与工程(Electric Power Science and Engineering)，2011，27(2):6-12.

[14] 卫志农，吴霜，孙国强，等(Wei Zhinong，Wu Shuang，Sun Guoqiang，et al.)．多目标电能质量监测器的优化配置(Optimal placement of power quality monitors based on multi-objective evolutionary algorithm)[J]．电网技术(Power System Technology)，2012，36(1)：176-181.

[15] 刘景远，刘卫明，李袖，等(Liu Jingyuan，Liu Weiming，Li Xiu，et al.)．一种电压暂降监测装置优化配置的方法(A method of optimal configuration for voltage sag monitoring devices)[J]．电测与仪表(Electrical measurement and instrumentation)，2014，5(11):120-125.

[16] 陈伟，赵锦苹(Chen Wei，Zhao Jinping)．复杂电网中电压跌落凹陷域的仿真分析(Simulation analysis on vulnerability area of voltage dip in complex power grid)[J]．电网技术(Power System Technology)，2014，38(5)：1322-1328.

[17] 肖湘宁，陶顺(Xiao Xiangning，Tao Shun)．中性点不同接地方式下的电压暂降类型及其在变压器间的传递(一)(Voltage sags types under different grounding modes of neutral and their propagation: Part I)[J]．电工技术学报(Transactions of China Electrotechnical Society)，2007，22(9)：143-148.

[18] 肖湘宁，陶顺(Xiao Xiangning，Tao Shun)．中性点不同接地方式下的电压暂降类型及其在变压器间的传递(二)(Voltage sags types under different grounding modes of neutral and their propagation: Part II)[J]．电工技术学报(Transactions of China Electrotechnical Society)，2007，22(10)：156-159.

[19] 陈瑞(Chen Rui)．电压暂降在配电网中的传播规律及其仿真评估研究(Research on propagation regularity and simulation assessment of voltage sags in distribution)[D]．北京：华北电力大学(Beijing：North China Electric Power University)，2006.

[20] 常学飞，田立军，秦英林(Chang Xuefei，Tian Lijun，Qin Yinglin)．一种精确确定电压暂降凹陷域的算法(Method to accurately determine vulnerable areas of voltage sag)[J]．电力自动化设备(Electric Power Automation Equipment)，2011，31(4)：64-68.

[21] 何仰赞，温增银(He Yangzan，Wen Zengyin)．电力系统分析(Power system analysis)[M]．武汉：华中科技大学出版社(Wuhan：Huazhong University of Science and Technology Press)，2002.

Optimum allocation method of power quality monitors by considering connection modes of transformers

LIU Ping, OUYANG Sen, CAI Dong-yang

(College of Electric Power, South China University of Technology, Guangzhou 510640, China)

The paper puts forward an optimum allocation method of power quality monitors by considering the connection modes of transformers to make up for deficiencies of the current method. Firstly, the paper deeply studied the effect of different connection modes of transformers on the propagation characteristics of voltage sags, and established the voltage sag amplitude matrix corresponding to the connection modes of transformers. Secondly, the voltage sag observable matrix was constructed at different types of faults, forming the constraint to ensure the voltage sags can be observed in the grid. Then, the optimum allocation method of power quality monitors based on genetic algorithm was put forward, which takes the least monitoring buses as its objective. At last, the effectiveness of proposed method was verified by the case study based on IEEE-39 standard test system.

connection mode of transformer； power quality monitor； observable matrix； configuration scheme； genetic algorithm

2015-08-25

国家自然科学基金资助项目(51377060)

刘 平 (1991-)， 男， 河南籍， 硕士研究生， 主要研究方向为电能质量分析与控制; 欧阳森 (1974-)， 男， 广西籍， 副研究员， 博士， 主要研究方向为电能质量、 节能技术及智能电器。

TM711

A

1003-3076(2016)05-0042-06